アクティブ・フィルタ
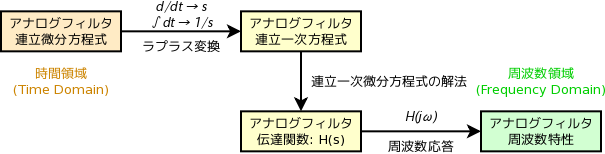
キルヒホッフの第一法則による連立方程式
多重帰還型(MFB)LPFを例に周波数特性の求め方を説明します。
(ただしここでは
OPアンプは理想OPアンプとします。)
上図のように電流 \( i_1 , i_2 , i_3 \) を定めると、オームの法則と静電容量の定義式 \( Q (= \int I \mathrm{ d } t ) = CV \) およびキルヒホッフの第一法則から、以下の連立方程式が得られます。
\( \begin{eqnarray} \left\{ \begin{array}{l} u = R_1 (i_1 + i_2 + i_3) + \frac{1}{C_1} \int i_1 \mathrm{d} t \\ u = R_1 (i_1 + i_2 + i_3) + R_2 i_2 \\ u = R_1 (i_1 + i_2 + i_3) + R_3 i_3 + y \\ 0 = \frac{1}{C_2} \int i_2 \mathrm{d} t + y \end{array} \right. \end{eqnarray} \)
上の連立方程式をラプラス変換すると、ラプラス変換の演算子 \( s \) により積分記号が消え、以下のように未知数 \( i_1 (s) \) , \( i_2 (s) \) , \( i_3 (s) \) , \( y(s) \) の連立一次方程式になります。
\( \begin{eqnarray} \left\{ \begin{array}{l} u(s) = R_1 \left(i_1 (s)+ i_2 (s)+ i_3 (s) \right) + \frac{1}{C_1 s} i_1 (s) \\ u(s) = R_1 \left(i_1 (s)+ i_2 (s)+ i_3 (s) \right) + R_2 i_2 (s) \\ u(s) = R_1 \left(i_1 (s)+ i_2 (s)+ i_3 (s) \right) + R_3 i_3 (s) + y(s) \\ 0 = \frac{1}{C_2 s} i_2 (s) + y(s) \end{array} \right. \end{eqnarray} \)
この連立一次方程式を解けば伝達関数が得られます。
GNU Octaveでの演算手順
GNU Octave は Excelなどの表計算ソフトとは違い、直接、複素数の行列演算が可能です。
ラプラス変換後の連立一次方程式を行列表記すると
\( \begin{bmatrix} u(s) \\ u(s) \\ u(s) \\ 0 \end{bmatrix} = \begin{bmatrix} R_1 + \frac{1}{C_1 s} & R_1 & R_1 & 0 \\ R_1 & R_1 + R_2 & R_1 & 0 \\ R_1 & R_1 & R_1 + R_3 & 1 \\ 0 & \frac{1}{C_2 s } & 0 & 1 \end{bmatrix} \begin{bmatrix} i_1 (s) \\ i_2 (s) \\ i_3 (s) \\ y(s) \end{bmatrix} \)
上の式中の正方行列を \(A\) として
\( A = \begin{bmatrix} R_1 + \frac{1}{C_1 s} & R_1 & R_1 & 0 \\ R_1 & R_1 + R_2 & R_1 & 0 \\ R_1 & R_1 & R_1 + R_3 & 1 \\ 0 & \frac{1}{C_2 s } & 0 & 1 \end{bmatrix} \)
連立一次方程式は
\( \begin{bmatrix} u(s) \\ u(s) \\ u(s) \\ 0 \end{bmatrix} = A \begin{bmatrix} i_1 (s) \\ i_2 (s) \\ i_3 (s) \\ y(s) \end{bmatrix} \)
これに左から \( A \) の逆行列 \( A^{-1} \) をかけて
\( A^{-1} \begin{bmatrix} u(s) \\ u(s) \\ u(s) \\ 0 \end{bmatrix} = \begin{bmatrix} i_1 (s) \\ i_2 (s) \\ i_3 (s) \\ y(s) \end{bmatrix} \)
更にに左から行ベクトル \( \begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix} \) をかければ出力 \( y(s) \) が得られます。
\( \begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix} A^{-1} \begin{bmatrix} u(s) \\ u(s) \\ u(s) \\ 0 \end{bmatrix} = y(s) \)
伝達関数による方法
伝達関数の求め方は、VCVSフィルタとMFBフィルタの
MFB(多重帰還型)フィルタで求めた方法以外に
キルヒホッフの第一法則による連立方程式の最後に示した連立一次方程式を解くことによっても可能です。
むしろキルヒホッフの第一法則から連立方程式を立て、ラプラス変換で連立一次方程式化し、これを解く方が、手順として一般化が可能な分有効な手法かと思います。
連立一次方程式の解法は GNU Octaveでの演算手順の冒頭のように行列化すれば、クラメールの公式を適用することで手順を更に一般化できます。
\( y(s) = \frac {\begin{vmatrix} R_1 + \frac{1}{C_1 s} & R_1 & R_1 & u(s) \\ R_1 & R_1 + R_2 & R_1 & u(s) \\ R_1 & R_1 & R_1 + R_3 & u(s) \\ 0 & \frac{1}{C_2 s } & 0 & 0 \end{vmatrix}} {\begin{vmatrix} R_1 + \frac{1}{C_1 s} & R_1 & R_1 & 0 \\ R_1 & R_1 + R_2 & R_1 & 0 \\ R_1 & R_1 & R_1 + R_3 & 1 \\ 0 & \frac{1}{C_2 s } & 0 & 1 \end{vmatrix}} \)
あとは行列式をひたすら解いていきます。ここでの行列式の計算が苦にさえならなければ、とても便利な方法です。ではまず分子から
\( \phantom {=} {\begin{vmatrix} R_1 + \frac{1}{C_1 s} & R_1 & R_1 & u(s) \\ R_1 & R_1 + R_2 & R_1 & u(s) \\ R_1 & R_1 & R_1 + R_3 & u(s) \\ 0 & \frac{1}{C_2 s } & 0 & 0 \end{vmatrix}} \\ = \frac{u(s)}{C_2 s} {\begin{vmatrix} R_1 + \frac{1}{C_1 s} & R_1 & 1 \\ R_1 & R_1 & 1 \\ R_1 & R_1 + R_3 & 1 \end{vmatrix}} \\ = \frac{u(s)}{C_2 s} {\begin{vmatrix} \frac{1}{C_1 s} & 0 & 0 \\ R_1 & R_1 & 1 \\ 0 & R_3 & 0 \end{vmatrix}} \\ = \frac{1}{C_1 s} \frac{1}{C_2 s} R_3 u(s) \)
次は分母を
\( \phantom {=} {\begin{vmatrix} R_1 + \frac{1}{C_1 s} & R_1 & R_1 & 0 \\ R_1 & R_1 + R_2 & R_1 & 0 \\ R_1 & R_1 & R_1 + R_3 & 1 \\ 0 & \frac{1}{C_2 s } & 0 & 1 \end{vmatrix}} \\ = {\begin{vmatrix} R_1 + \frac{1}{C_1 s} & R_1 & R_1 \\ R_1 & R_1 + R_2 & R_1 \\ R_1 & R_1 - \frac{1}{C_1 s} & R_1 + R_3 \end{vmatrix}} \\ = {\begin{vmatrix} R_1 + \frac{1}{C_1 s} & - \frac{1}{C_1 s} & - \frac{1}{C_1 s} \\ R_1 & R_2 & 0 \\ R_1 & - \frac{1}{C_2 s} & R_3 \end{vmatrix}} \\ = R_1 \frac{1}{C_1 s} ( R_2 + \frac{1}{C_2 s} ) + R_3 \left( (R_1 + \frac{1}{C_1 s} ) R_2 + R_1 \frac{1}{C_1 s} \right) \)
したがって多重帰還型(MFB)LPF の伝達関数は
\begin{eqnarray} \frac{y(s)}{u(s)} = \frac{ - \frac{1}{C_1 s} \frac{1}{C_2 s} R_3 } { R_1 \frac{1}{C_1 s} ( R_2 + \frac{1}{C_2 s} ) + R_3 \left( (R_1 + \frac{1}{C_1 s} ) R_2 + R_1 \frac{1}{C_1 s} \right) } \\ \phantom{ \frac{y(s)}{u(s)} } = \frac{ -R_3 } { R_1 \left( R_2 R_3 C_1 C_2 s^2 + \left( R_2 + R_3 + \frac{R_2 R_3}{R_1} \right) C_2 s + 1 \right)} \end{eqnarray}
GNU Octaveスクリプトとgnuplot
実際に
GNU Octave
で周波数特性を計算し
gnuplotを呼びだしグラフ表示させた例を示します。GNU Octaveでの演算手順と伝達関数による方法の両方で計算し出力しています。
(回路定数はTexas Instruments 8-channel Audio DAC PCM1691 のデータシート記載された
Typical Post-LPF
値を使用しました。)
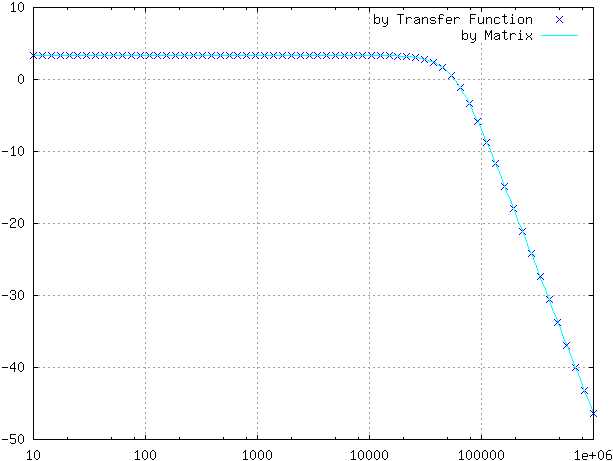
以下 GNU Octave のスクリプトです。
clear -all R1=5.1e3; R2=470; R3=7.5e3; C1=4.7e-9; C2=4.7e-10; f1=logspace(1,6,64); for k=1:64 s=2*pi*f1(k)*j; y=-R3/R1/(R2*R3*C1*C2*s*s+(R2+R3+R2*R3/R1)*C2*s+1); y1dB(k)=20*log10(abs(y)); end f2=logspace(1,6,256); for k=1:256 s=2*pi*f2(k)*j; A=[R1+1/C1/s R1 R1 0; R1 R1+R2 R1 0; R1 R1 R1+R3 1; 0 1/C2/s 0 1]; b=[1;1;1;0]; y=[0 0 0 1]*inv(A)*b; y2dB(k)=20*log10(abs(y)); end semilogx(f1,y1dB,'xb;by Transfer Function;',f2,y2dB,'c;by Matrix;') axis([10,1000000,-50,10]) grid on
- 平衡入力MFBフィルタ
- (PREV)
- GNU Octaveで求める周波数特性
- (NEXT)
- 2次LPFのステップ応答