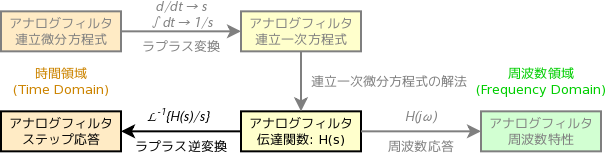
アクティブ・フィルタ

• VCVSフィルタとMFBフィルタ
  | 
• 平衡入力MFBフィルタ
  | 
• GNU Octaveで求める周波数特性
  | 
• 2次LPFのステップ応答

2次LPFのステップ応答

VCVS LPFの伝達関数

簡単のため

$H\left(\mathrm{s}\right)=\frac{{{\omega }_C}^2}{{\mathrm{s}}^2+\frac{{\omega }_C}{Q}\mathrm{s}+{{\omega }_C}^2}$

$\mathrm{s}\leftarrow i\omega$

$H\left(i\omega \right)=\frac{{{\omega }_C}^2}{-{\omega }^2+i\frac{{\omega }_C}{Q}\omega +{{\omega }_C}^2}=\frac{{{\omega }_C}^2\left({{\omega }_C}^2-{\omega }^2-i\frac{{\omega }_C}{Q}\omega \right)}{{\left({{\omega }_C}^2-{\omega }^2\right)}^2+{\left(\frac{{\omega }_C}{Q}\omega \right)}^2}$

$\left|H\left(i\omega \right)\right|=\frac{1}{\sqrt{{\left(\frac{\omega }{{\omega }_C}\right)}^4+\left(\frac{1}{Q^2}-2\right){\left(\frac{\omega }{{\omega }_C}\right)}^2+1}}$

ステップ応答

伝達関数 H(s) に単位ステップ 1 / s をかけラプラス逆変換します。

$\frac{H\left(\mathrm{s}\right)}{\mathrm{s}}=\frac{{{\omega }_C}^2}{\mathrm{s}\left({\mathrm{s}}^2+\frac{{\omega }_C}{Q}\mathrm{s}+{{\omega }_C}^2\right)}$

(1) Q = 0.5 ( ζ ( = 1 / 2Q ) = 1 ) のとき

$\frac{H\left(\mathrm{s}\right)}{\mathrm{s}}=\frac{a^2}{\mathrm{s}{\left(\mathrm{s}+a\right)}^2}$ とおくと

$\begin{array}{ll}\frac{H\left(\mathrm{s}\right)}{\mathrm{s}}& =\frac{a}{\mathrm{s}\left(\mathrm{s}+a\right)}-\frac{a}{{\left(\mathrm{s}+a\right)}^2}\\ & =\frac{1}{\mathrm{s}}-\frac{1}{\mathrm{s}+a}-\frac{a}{{\left(\mathrm{s}+a\right)}^2}\end{array}$

ラプラス変換表より

${\mathcal{L}}^{-1}\left[\frac{1}{\mathrm{s}}\right]=1$ , ${\mathcal{L}}^{-1}\left[\frac{1}{\mathrm{s}+a}\right]={\mathrm{e}}^{-at}$ , ${\mathcal{L}}^{-1}\left[\frac{a}{{\left(\mathrm{s}+a\right)}^2}\right]=t{\mathrm{e}}^{-at}$

${\mathcal{L}}^{-1}\left[\frac{H\left(\mathrm{s}\right)}{\mathrm{s}}\right]=1-{\mathrm{e}}^{-at}-at{\mathrm{e}}^{-at}=1-\left(1+at\right){\mathrm{e}}^{-at}$

(2) Q < 0.5 ( ζ ( = 1 / 2Q ) > 1 ) のとき

$\frac{H\left(\mathrm{s}\right)}{\mathrm{s}}=\frac{ab}{\mathrm{s}\left(\mathrm{s}+a\right)\left(\mathrm{s}+b\right)}$ とおくと

$\begin{array}{ll}\frac{H\left(\mathrm{s}\right)}{\mathrm{s}}& =\frac{ab}{\mathrm{s}}\left(\frac{1}{b-a}\right)\left(\frac{1}{\mathrm{s}+a}-\frac{1}{\mathrm{s}+b}\right)\\ & =\frac{ab}{b-a}\left\{\frac{1}{\mathrm{s}\left(\mathrm{s}+a\right)}-\frac{1}{\mathrm{s}\left(\mathrm{s}+b\right)}\right\}\\ & =\frac{ab}{b-a}\left\{\frac{1}{a}\left(\frac{1}{\mathrm{s}}-\frac{1}{\mathrm{s}+a}\right)-\frac{1}{b}\left(\frac{1}{\mathrm{s}}-\frac{1}{\mathrm{s}+b}\right)\right\}\\ & =\frac{1}{\mathrm{s}}-\frac{b}{b-a}·\frac{1}{\mathrm{s}+a}+\frac{a}{b-a}·\frac{1}{\mathrm{s}+b}\end{array}$

ラプラス変換表より

${\mathcal{L}}^{-1}\left[\frac{1}{\mathrm{s}}\right]=1$ , ${\mathcal{L}}^{-1}\left[\frac{1}{\mathrm{s}+a}\right]={\mathrm{e}}^{-at}$

${\mathcal{L}}^{-1}\left[\frac{H\left(\mathrm{s}\right)}{\mathrm{s}}\right]=\frac{a\left(1-{\mathrm{e}}^{-bt}\right)-b\left(1-{\mathrm{e}}^{-at}\right)}{a-b}$

(3) Q > 0.5 ( ζ ( = 1 / 2Q ) < 1 ) のとき

$\frac{H\left(\mathrm{s}\right)}{\mathrm{s}}=\frac{a^2+b^2}{\mathrm{s}\left\{{\left(\mathrm{s}+a\right)}^2+b^2\right\}}$ とおくと

$\begin{array}{ll}\frac{H\left(\mathrm{s}\right)}{\mathrm{s}}& =\frac{a^2+b^2}{\mathrm{s}}·\frac{1}{\left\{\left(\mathrm{s}+a\right)-ib\right\}\left\{\left(\mathrm{s}+a\right)+ib\right\}}\\ & =\frac{a^2+b^2}{\mathrm{s}}·\frac{1}{i2b}\left\{\frac{1}{\left(\mathrm{s}+a\right)-ib}-\frac{1}{\left(\mathrm{s}+a\right)+ib}\right\}\\ & =\frac{a^2+b^2}{i2b}\left(\frac{1}{\mathrm{s}}·\frac{1}{\mathrm{s}+a-ib}-\frac{1}{\mathrm{s}}·\frac{1}{\mathrm{s}+a+ib}\right)\\ & =\frac{a^2+b^2}{i2b}\left\{\frac{1}{a-ib}\left(\frac{1}{\mathrm{s}}-\frac{1}{\mathrm{s}+a-ib}\right)-\frac{1}{a+ib}\left(\frac{1}{\mathrm{s}}-\frac{1}{\mathrm{s}+a+ib}\right)\right\}\\ & =\frac{a^2+b^2}{i2b}\left(\frac{i2b}{a^2+b^2}·\frac{1}{\mathrm{s}}-\frac{1}{a-ib}·\frac{1}{\mathrm{s}+a-ib}+\frac{1}{a+ib}·\frac{1}{\mathrm{s}+a+ib}\right)\\ & =\frac{1}{\mathrm{s}}-\frac{a+ib}{i2b}·\frac{1}{\mathrm{s}+a-ib}+\frac{a-ib}{i2b}·\frac{1}{\mathrm{s}+a+ib}\end{array}$

${\mathcal{L}}^{-1}\left[\frac{H\left(\mathrm{s}\right)}{\mathrm{s}}\right]=1-\frac{a+ib}{i2b}·{\mathrm{e}}^{-at}{\mathrm{e}}^{ibt}+\frac{a-ib}{i2b}·{\mathrm{e}}^{-at}{\mathrm{e}}^{-ibt}=1-{\mathrm{e}}^{-at}\left(\cos bt+\frac{a}{b}\sin bt\right)$

　

尖鋭度(Q)	減衰係数(ζ)	Overshoot & Ringing	備考
Q > 0.5	0 < ζ < 1	あり	減衰振動(dumping oscillation)
Q = 0.5	ζ = 1	なし	臨界減衰(critical dumping)
Q < 0.5	ζ > 1	なし	過減衰(Over dumping)

ステップ応答と位相余裕

減衰振動(dumping oscillation)の応答をf(t)

$f\left(t\right)=1-e^{-at}\left(\cos bt+\frac{a}{b}\sin bt\right)$

とおき時間:t で微分してステップ応答のピークの時間を求めます。

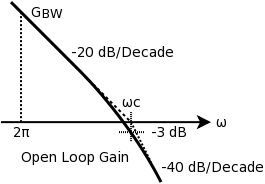
ゲイン無限大で利得帯域幅積:G_BW の積分特性に一次の2ndポール:ω_C を加えた伝達関数:G(s) を評価モデルとします。

$G\left(\mathrm{s}\right)=\frac{2\pi G_{\mathit{BW}}}{\mathrm{s}}\times \frac{{\omega }_C}{\mathrm{s}+{\omega }_C}$

このOP-Ampに100%フィードバックを掛けてボルテージ・フォロアにしたときの閉ループ伝達関数:H(s) は

$H\left(\mathrm{s}\right)=\frac{G\left(\mathrm{s}\right)}{G\left(\mathrm{s}\right)+1}=\frac{2\pi G_{\mathit{BW}}{\omega }_C}{{\mathrm{s}}^2+{\omega }_C\mathrm{s}+2\pi G_{\mathit{BW}}{\omega }_C}$

これに減衰振動(Q > 0.5)する2次系伝達関数にあてはめると

$a=\frac{{\omega }_C}{2}$

$a^2+b^2=2\pi G_{\mathit{BW}}{\omega }_C$

$1+\frac{b^2}{a^2}=\frac{4}{{{\omega }_C}^2}\times 2\pi G_{\mathit{BW}}{\omega }_C$

$\frac{a}{b}=\frac{1}{\sqrt{\frac{8\pi G_{\mathit{BW}}}{{\omega }_C}-1}}$

$f\left(\frac{\pi }{b}\right)-1=exp\left(\frac{-\pi }{\sqrt{\frac{8\pi G_{\mathit{BW}}}{{\omega }_C}-1}}\right)$

$\frac{8\pi G_{\mathit{BW}}}{{\omega }_C}=1+{\left(\frac{\pi }{\ln \left(f\left(\frac{\pi }{b}\right)-1\right)}\right)}^2$

オープンループの周波数特性は

$G\left(i\omega \right)=\frac{2\pi G_{\mathit{BW}}{\omega }_C}{-{\omega }^2+i{\omega }_C\omega }=\frac{\left(-{\omega }^2+i{\omega }_C\omega \right)2\pi G_{\mathit{BW}}{\omega }_C}{{\omega }^4+{{\omega }_C}^2{\omega }^2}$

オープンループ・ゲインを 1とおいて

$\left|G\left(i\omega \right)\right|=\frac{2\pi G_{\mathit{BW}}{\omega }_C}{\sqrt{{\omega }^4+{{\omega }_C}^2{\omega }^2}}=\frac{2\pi G_{\mathit{BW}}{\omega }_C}{\omega \sqrt{{\omega }^2+{{\omega }_C}^2}}=1$

$4{\pi }^2{G_{\mathit{BW}}}^2{{\omega }_C}^2={\omega }^4+{{\omega }_C}^2{\omega }^2$

2次方程式の解の公式から

${\omega }^2=\frac{-{{\omega }_C}^2+\sqrt{{{\omega }_C}^4+16{\pi }^2{G_{\mathit{BW}}}^2{{\omega }_C}^2}}{2}$

$\omega ={\omega }_C\sqrt{\frac{-1+\sqrt{1+\frac{16{\pi }^2{G_{\mathit{BW}}}^2}{{{\omega }_C}^2}}}{2}}={\omega }_C\sqrt{\frac{-1+\sqrt{1+{\left(\frac{4\pi G_{\mathit{BW}}}{{\omega }_C}\right)}^2}}{2}}=\frac{{\omega }_C}{2}\sqrt{-2+\sqrt{4+{\left(\frac{8\pi G_{\mathit{BW}}}{{\omega }_C}\right)}^2}}$

位相余裕は

$\frac{\pi }{2}-arctan\left(\frac{1}{2}\sqrt{-2+\sqrt{4+{\left(\frac{8\pi G_{\mathit{BW}}}{{\omega }_C}\right)}^2}}\right)$

$=\frac{\pi }{2}-arctan\left(\frac{1}{2}\sqrt{-2+\sqrt{4+{\left(1+{\left(\frac{\pi }{\ln \left(f\left(\frac{\pi }{b}\right)-1\right)}\right)}^2\right)}^2}}\right)$