平衡入力MFBフィルタ

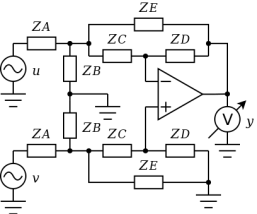
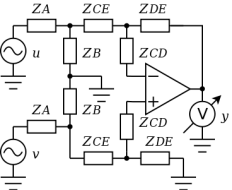
アクティブ・フィルタ

MFBフィルタの平衡入力化

MFBフィルタが平衡(バランス)入力化できることを知ったのはTexas InstrumentsのPCM DAC PCM1791AのデータシートのポストLPFです。実はちょっとした衝撃でしたが…

解析の内容は途中までMFB(多重帰還型)フィルタと、まったく同じなのですが一応再度ここにも記載します。

左図の回路の Z_C, Z_D, Z_Eをデルタ・スター変換します。

$Z_{CE} = \frac{Z_{C} Z_{E}}{Z_{C} + Z_{D} + Z_{E}}$

$Z_{DE} = \frac{Z_{D} Z_{E}}{Z_{C} + Z_{D} + Z_{E}}$

$Z_{CD} = \frac{Z_{C} Z_{D}}{Z_{C} + Z_{D} + Z_{E}}$

左図の回路の Z_A, Z_B, Z_CEをスター・デルタ変換します。

$Z_{ACE} = \frac{Z_{A} Z_{B} + Z_{B} Z_{CE} + Z_{CE} Z_{A}}{Z_{B}}$

$Z_{A B} = \frac{Z_{A} Z_{B} + Z_{B} Z_{CE} + Z_{CE} Z_{A}}{Z_{CE}}$

$Z_{BCE} = \frac{Z_{A} Z_{B} + Z_{B} Z_{CE} + Z_{CE} Z_{A}}{Z_{A}}$

理想OPアンプでは入力インピーダンスは無限大なので Z_CDは無視できます。 Z_ABは単なる入力信号の負荷なので無視できます。ここまではMFB(多重帰還型)フィルタとまったく同じです。

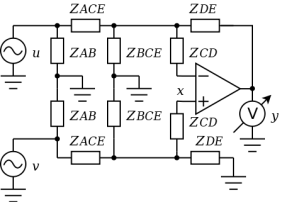
Z_CDを無視したとき、非反転入力 xは重ね合わせの理から

$x = \frac{Z_{BCE} Z_{DE} \times u + Z_{ACE} Z_{BCE} \times y}{Z_{ACE} Z_{BCE} + Z_{BCE} Z_{DE} + Z_{DE} Z_{ACE}}$

また反転入力 xは

$x = \frac{Z_{BCE} Z_{DE} \times v}{Z_{ACE} Z_{BCE} + Z_{BCE} Z_{DE} + Z_{DE} Z_{ACE}}$

よって

$y = \frac{Z_{DE} (v - u)}{Z_{ACE}}$

更なる素子の削減

左図は前セクション最初の回路の Z_Bの片側をGNDの代わりに電圧源 $w$ に接続したものです。

この回路についても Z_C, Z_D, Z_Eをデルタ・スター変換し、次に Z_A, Z_Bとデルタ・スター変換で得られた Z_CEを前セクションと同様にスター・デルタ変換します。

左図はスター・デルタ変換後の回路です。

前セクション同様に Z_CDと Z_ABを無視したとき、非反転入力 xは重ね合わせの理から

x = \frac{Z_{ACE} Z_{BCE} \times y + Z_{BCE} Z_{DE} \times u + Z_{DE} Z_{ACE} \times w}{Z_{ACE} Z_{BCE} + Z_{BCE} Z_{DE} + Z_{DE} Z_{ACE}}

また反転入力 xは

x = \frac{Z_{BCE} Z_{DE} \times v + Z_{DE} Z_{ACE} \times w}{Z_{ACE} Z_{BCE} + Z_{BCE} Z_{DE} + Z_{DE} Z_{ACE}}

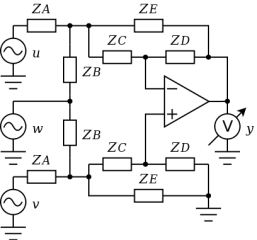
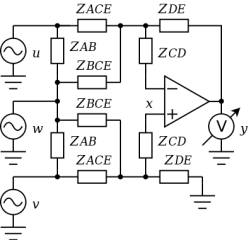
ゲイン無限大の理想OPアンプとして [反転入力]=[非反転入力] から式を整理すると

y = \frac{Z_{DE} (v - u)}{Z_{ACE}} = \frac{\frac{Z_{D} Z_{E}}{Z_{C} + Z_{D} + Z_{E}} (v - u)}{\frac{Z_{A} Z_{B} + (Z_{A} + Z_{B}) \frac{Z_{C} Z_{E}}{Z_{C} + Z_{D} + Z_{E}}}{Z_{B}}} = \frac{Z_{B} Z_{D} Z_{E} (v - u)}{Z_{A} Z_{B} (Z_{C} + Z_{D} + Z_{E}) + (Z_{A} + Z_{B}) Z_{C} Z_{E}}

電圧源 wの成分は相殺され出力には表れないので wは任意の値をとれます。ここで仮りに2個の Z_Bの電流(電圧)が常に等しくなるようにトラッキングする電圧源 wを考えます。このとき電圧源 wからは電流がまったく供給されません。つまり0Vの電圧源であるGNDを含め電圧源はまったく必要なかったということになります。

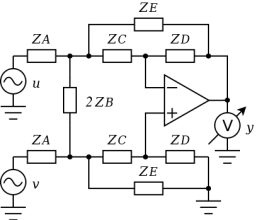
よって、左図のように2個の Z_Bは2倍のインピーダンスの素子1個に置き換えることが可能です。

$Z_{A} (s) = R_{1} (= R_{2})$

$Z_{B} (s) = \frac{1}{2 C_{1} s}$

$Z_{C} (s) = R_{5} (= R_{6})$

$Z_{B} (s) = \frac{1}{C_{2} s} (= \frac{1}{C_{3} s})$

$Z_{E} (s) = R_{3} (= R_{4})$

とすると伝達関数は

\frac{y (s)}{v (s) - u (s)} = \frac{R_{3}}{R_{1} (2 R_{3} R_{5} C_{1} C_{2} s^{2} + (R_{3} + R_{5} + \frac{R_{3} R_{5}}{R_{1}}) C_{2} s + 1)}

VCVSフィルタとMFBフィルタ
(PREV)

平衡入力MFBフィルタ

(NEXT)
GNU Octaveで求める周波数特性