(Fig.1) Quantum mechanics unable to explain molecular van der Waals attraction and Pauli repulsion "regresses" to one pseudo-electron model = DFT. → Science stops forever.

The current only atomic theory = quantum mechanics is amazingly "unsuccessful" and filled with so many paradoxes and unreality that even the founder Schrödinger himself thought quantum mechanics was a farce.
Of course, his hunch that quantum mechanics was a total science fiction turned out to be right (this p.4-3rd-paragraph ).
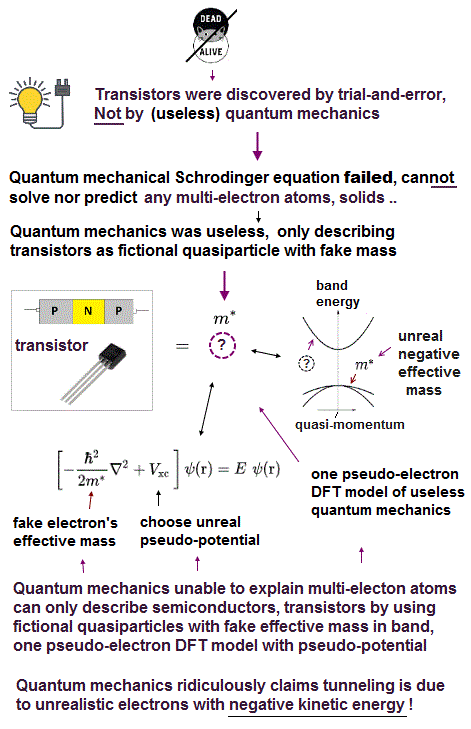
Contrary to the media-hype and their exaggerated narratives, quantum mechanics has been completely useless, rather, harmful (= by preventing our real scientific progress ) in all science field such as computer transistor, smartphone, parallel-world quantum computers and medicine.
All quantum mechanical physicists can do is show a pie-in-the-sky goal or imaginary rosy future, hyping the still-impractical fictional computers without making public any detailed data about thier dubious performance ( this 3rd paragraph ).The only calculation tool of quantum mechanics is Schrödinger equation which is infamously unsolvable and unable to give the exact real wavefunctions in all multi-electron atoms and molecules ( this p.21 ).
We have rigorously proved that we can Never solve any multi-electron Schrödinger equations satisfying conservation of total energy E (= kinetic + potential energies ) or quantum mechanical requirement of Pauli antisymmetric wavefunctions, so quantum mechanics is officially proved to be false.
According to quantum mechanical Pauli principle antisymmetric artificial rule (= No physical meaning, this p.3-4 ), the space wavefunction between the opposite spins (= spin part is antisymmetric ) must be symmetric cauising fictitious molecular attractive exchange energy (= due to fictitious lower kinetic energy ), and the space wavefunction between the same spin (= spin part is symmetric ) must be antisymmetric causing Pauli repulsive exchange energy (= due to fictitious higher kinetic energy ).
↑ But this quantum mechanical Pauli antisymmetric wavefunctions can Not express atoms or molecules with more than two electrons combining up-spins and down-spins (= combining wavefunctions of the symmetric between the opposite spins and antisymmetric between the same spin ) such as Lithium.
So quantum mechanics unreasonably gave up only the symmetric wavefunctions between the opposite spins (= which means giving up the molecular attractive exchange energies = No molecular bond ! ), and its antisymmetric wavefunctions expressed as Slatar determinants give only the unneeded Pauli repulsion, as shown in the failed molecular orbital (= MO ) theory which disagrees with the actual molecules.
Hence, all the multi-electron Schrodinger equations incorporating paradoxical Pauli antisymmetric wavefunctions completely failed.
Physicists were forced to choose the more unrealistic one-pseudo-electron density functional theory (= DFT ) as the only (pseudo-)quantum mechanical calculation method, which also has fatal flaws.
In the original unsolvable multi-electron Schrödinger equations, physicists have to artificially choose fake arbitrary approximate solutions or basis sets with many freely-adjustable parameters out of infinite choices using quantum mechanical variational methods which cannot predict any physical values (= because they just choose fake solutions, and do Not know the chosen wavefunctions may give energies close to actual ones, until they compare the calculated results with experimental values ), so completely useless in any applied science.
Physicists have No way to know the exact atomic or molecular energies until they actually measure physical values in experiments. ← This means it is far better to use the experimentally-obtained data from the beginning instead of wasting time in quantum mechanical impractically time-consuming ad-hoc methods ( this 2nd-last paragraph ).
Even the approximate methods of just choosing fake solutions called "trial wavefunctions" or "basis set functions ( this p.12-22 )" and integrate them with Schrödinger equations are extremely time-consuming, so quantum mechanical methods, even in its ad-hoc arbitrary approximate methods, cannot deal with even a simple nitrogen atom ( this p.11 ).
No matter what (fake) trial wavefunctions or basis sets are artificially chosen as the seeming approximate wavefunctions, these chosen wavefunctions can never be true solutions satisfying the original multi-electron Schrodinger equations, due to their obvious violation of total energy conservation law.
The problem is quantum mechanical wavefunction or orbital itself has No physical reality ( this last-paragraph, this p.8 ), hence, it's impossible to know the real physical phenomena from these unreal quantum mechanical wavefunctions.
The present quantum chemistry has deep flaws about its notions of bonds ( this p.2 lower )
Physicists have heavily relied on various semi-empirical fictitious models whose parameters needed to be artificially fitted to experimentally-obtained data ( this p.4-2nd paragraph ) in molecular σ and π bonds such as Huckel methods ( this 2nd-paragraph, this p.4-2nd-last-paragraph ) and empirical effective nuclear charges instead of predicting physical values from the useless quantum mechanics ( this p.3-right-last~p.4 ).
↑ The so-called "ab-initio" or "first-principle" phrases are often misleadingly abused for making the inherently-useless quantum mechanics appear to have some (fictional) power to predict values, though it doesn't have ( this p.17, this p.23, this p.6-2nd-paragaraph, this p.8-upper ).
Because all quantum mechanical methods need some artificial models or approximate wavefunctions with free parameters, which must be adjusted by chosen models, methods and experiments, due to inherently-unsolvable Schrödinger equations which cannot predict anything.
Furthermore, the useless quantum mechanics has Not clarified any real physical mechanisms behind chemical bonds ( this p.13-last paragraph ).
The most serious irreparable flaws of quantum mechanics is its probability wavefunction or electron cloud thinly spreading out throughout all space cannot describe actual Coulomb electric attraction or repulsion in chemical bonds, unlike a realistic movable electron particle.
Because a quantum mechanical electron has to be always distributed symmetrically around each nucleus, unable to move to the left or right side of the nucleus. ← An unmovable quantum mechanical electron is unable to avoid the other negative electrons or attract the other positive nucleus to cause Coulomb attractive energies strong enough for molecular covalent bonds.
Hence, quantum mechanical spreading wavefunctions or electron clouds have to rely on the artificially-introduced unphysical "exchange energies" for generating fictitious molecular bond energies, which mysterious exchange energies expressed by exchange integral have No physical reality or involve No real force ( this p.8-lower, this p.11, this p.5-last, this p.4-5-fig.1 ).
Because the unphysical exchange energy requires the electron's kinetic energy to magically decrease or increase by constructively or destructively interfering wavefunctions to cause fictitious molecular bond attraction and Pauli repulsion without real forces involved ( this p.9-10 ).
↑ We actually compute and show this pseudo-kinetic energy change plays a major part in the quantum mechanical molecular attractive and Pauli repulsive energies by violating energy conservation law (= so quantum mechanics is false ), later.
In the quantum mechanical unphysical probability wavefunction, each electron is Not a actually-movable particle but a static electron cloud (= contradicting the notion of kinetic energy ) where an electron's charge is divided into infinitely small pieces and distributed symmetrically and continuously (= Not discretely ) in all space.
The problem is that this unrealistically divided and spread quantum mechanical wavefunction has No ability to explain the actual atomic electrical polarization, affinity or molecular bonds without introducing fictitious partial atomic charges ( this p.5-(19) ).
Because the mechanism of quantum mechanical molecular attraction is based on the electron's wavefunction penetrating the other electron's wavefunction (= collection of infinitely small charges spherically distributed ), as shown in the charges penetrating the other spherically distributed charges (= other electron's wavefunction ), which no longer experience repulsions from the outside (= other electron's wavefunction ) charges (→ the other nuclear attraction is slightly dominant ).
↑ Quantum mechanical thinly-spreading electron cloud or wavefunction is completely different from the realistic discrete-charge electrons which are moving and avoiding other discrete electrons (= a real electron is Not infinitely small charge ) to cause the realistic molecular bond attraction.
No matter how close we get to this continuously-spreading electron's cloud or quantum mechanical wavefunction, we observe Not an actual discrete electron charged particle but the infinitesimally-dividied and thinly-spreading charge cloud which cannot generate strong Coulomb repulsion between electron clouds, unlike two real discreate electrons close to each other easily generating strong repulsion.
↑ This discrepancy causes serious contradictions in quantum mechanical atoms and molecular bonds expressed by unrealistic wavefunctions or electron clouds.
Regardless of the distance between two electron clouds or wavefunctions, each electron cloud always remains the same thinly-spreading electron cloud consisting of infinitely-divided small charges, unlike the fact that each discrete electron charge's property or influence is stronger and more obvious as the distance between two real discrete electrons is shorter.
Hence, in the quantum mechanical thinly-spreading electron clouds or wavefunctions, molecular attractive bonds have to be stronger between smaller atoms with more valence electrons packed in smaller regions (= denser electron clouds should generate stronger molecular bonds in quantum mechanics ).
↑ Higher-density electron charged clouds are more likely to get closer to the positive nuclei and form the shorter and stronger molecular attractive bonds by penetrating the other atomic electron's infinitesimally-divided, thinly spreading electron clouds without causing actually-strong Coulomb repulsion between two discrete electron particles, each of which real electron concentrates the discrete finite charge -e (= Not infinitely smaller charge thinly-spreading out like quantum mechanical unreal electron cloud ) on itself.
In the actual molecular bonds, the molecular attractive bond energies of H-H (= hydrogen-hydrogen bond with only 2 electrons = 432 kj/mol ) and H-O (= hydrogen-oxygen bond with the total 7 valence electrons = 459 kj/mol ) are stronger than O-F (= oxygen-fluorine bond with the total 13 valence electrons = only 190 kj/mol ) and F-F (= fluorine-fluorine bond with the total 14 valence electrons = only 155 kj/mol ).
↑ These actual molecular bond energies clearly contradict quantum mechanical wavefunctions, because a fluorine F packing 7 valence electrons into the smaller region around it should form a stronger molecular bond by concentrating more electrons between two nuclei than a hydrogen atom with only one electron.
And the compart F-F (= fluorine-fluorine ) attractive bond energy is smaller than larger Cl-Cl bond (= chlorine-chlorine ), though the smaller F-F bond has the denser electron cloud (= hence, it should exert stronger attractive energy by dense electron clouds closer to two positive nuclei ) than the larger Cl-Cl ( this p.3 ).
↑ These electronic charge polarization and electronegativity affected by different pairs of atoms of a diatomic molecule cannot be explained by quantum mechanical wavefunction or electron cloud where each electron charge is infinitely divided and thinly, continuously spread out in all space ( this p.3-last, ) even by using additional artificial assumptions ( this p.9, this p.13 ).
Only the realistic electron charged particle, whose fundamental charge -e is discrete, not infinitely divided, can explain the atomic polarization and why the compact F atom tends to strongly repel other F atoms (= more discrete valence electrons tend to approach each other and cause stronger Coulomb repulsion in F-F bond ) and strongly attract H atoms (= H atomic single electron can easily avoid other electrons by moving to the opposite side of the nucleus, and exposing the positive nucleus to other electrons )
Also in intermolecular noncovalent bonds, if quantum mechanical symmetrically-spreading wavefunction or electron cloud was right, helium with two electrons should have formed more stronger intermolecular bonds with other molecular atoms than the strongest intermolecular hydrogen-bond by one-electron hydrogen (= in the intermolecular noncovalent bonds, Pauli repulsion, which has already applied in both in H- and He intermolecular bonds, doesn't need to be considered in this comparison ).
↑ The actual strong hydrogen bond can be perfectly explained by the realistic movable electron model where one electron of hydrogen atom can more easily move to the other side of nucleus to avoid other electrons than a two-electron helium atom which can only form extremely weaker van der Waals attraction than the hydrogen bond.
Physicists tried to express fictitious Coulomb electric force between an artifically-ionized (= excited ) slightly-positive wavefunction and a slightly-negative wavefunction ( this p.9 ) using various fictional model such as quasi-classical electrostatic attraction and the ad-hoc molecular orbital (= MO ) theory.
The problem is the weak Coulomb electric or van der Waals attractions are observed even between two completely-neutral non-polarized noble gas atoms such as helium-helium and neon-neon, which cannot be explained by the quantum mechanical static artificially-ionized wavefunctions or fictitious partial atomic charges.
So London discarded the conventional quantum mechanical atomic picture, and proposed the classical-like atomic model where electrons are actually moving and fluctuating around each nucleus, transiently generating the electric dipoles and van der Waals attraction even between neutral, nonpolarized atoms.
Quantum mechanics states Pauli repulsion allegedly generated between two electrons with the same spin must be described by (unphysical) antisymmetric wavefunctions. ← No more detailed explanation is given
↑ But this Pauli principle expressed by quantum mechanical antisymmetric wavefunctions cannot explain actual strong intermolecular Pauli repulsion which should prevent three or four hydrogen atoms from forming unreal H3 or H4 molecules.
Quantum mechanical molecular orbital (= MO ) theory is also unrealistic, MO can neither generate the normal molecular attractive exchange bond nor eliminate the unnecessary Pauli repulsive exchange energy, hence, all multi-electron quantum mechanical models failed to explain actual molecular bonds.
So physicists have to rely on various empirical pseudo-potential energy models such as Lennard-Jones potential whose parameters must be artificially adjusted compared to experiments with No theoretical basis by useless quantum mechanical theory.
In fact, this Pauli antisymmetric wavefunctions have fatal flaws, they cannot explain molecular bond attractive exchange energies which should be generated between two electrons with the opposite spins.
Pauli antisymmetric wavefunction can only describe Pauli repulsion, can Not describe molecular attraction or the multi-electron wavefunctions mixing Pauli repulsion and molecular attraction (= this important fact is often ignored in textbooks ), because antisymmetric wavefunction always eliminates positive attractive exchange energy or integral in two electrons with the opposite spins ( this p.6-upper ).
↑ This serious intrinsic defect of Pauli antisymmetric wavefunction exchanging different electrons unable to describe molecular attractive bonds ( when there are more than two electrons in the system ) forced physicsts to reluctantly choose the most primitive and unrealistic one-pseudo-electron density functional theory or DFT as the only quantum mechanical approximate method of describing multi-electron molecules or materials.
Quantum mechanics unable to solve the exact Schrödinger equations tries to create and choose many types of fake trial wavefunctions or basis sets to describe various molecular covalent bond energies, which artificial method is just "art" Not science.
These chosen basis set = fictitious wavefunctions whose parameters adjusted specifically for covalent molecular bonds often fail to explain the actual intermolecular noncovalent bond energies (= choosing fictitious atomic wavefunctions fitted for both covalent and non-covalent bonds at the same time is extremely difficult ).
These chosen wavefunctions combined with the artificially-chosen intermolecular pseudo-potential energies (such as Lennard Jones potential ) or DFT pseudo-potential functionals often cause many problems such as unrealistically larger van der Waals noncovalent attraction due to illegitimately lower kinetic and total energy than the experimental values relating to their spreading electron clouds (= basis set superposition error or BSSE, this p.3, this p.16-17 ). ← Quantum mechanical (fake) prediction based on variational method collapses.
This fatal errors and disagreement between quantum mechanics and actual intermolecualr energies are called "basis set superposition error (= BSSE ), which errors must be artificially removed using the fictitious Ghost atoms or counterpoise (= with only fictitious electron's orbital with No nucleus. this p.6, this p.8-computational method-2nd-paragraph ).
↑ The original quantum mechanical Schrödinger equation, atomic and molecular wavefunctions expressed as unphysical Pauli antisymmetric wavefunctions failed, so physicists had to artificially create various ad-hoc pseudo-potential energies including DFT functionals, and apply these pseudo-potentials to artificially-divided molecular energies (= energy decomposition or supermolecular approach ) using various free-parameters such as fictitious atomic charge, polarization, Pauli repulsive exchange (= No theoretical justificaion either in quantum mechanics or classical, this p.3-left, this p.2-left-lower ), dispersion energies, and BSSE ghost counterpoise ( this p.2-4, this p.6-7, this p.3 ).
The original quantum mechanical method is the conventional valence bond or Heitler-London (anti)symmetric molecular attractive ( or Pauli repulsive ) wavefunctions, which are used to calculate H2 molecular bond and anti-bond.
But this conventional quantum mechanical valence bond or Heitler-London method cannot be applied to atoms or molecules with more than two electrons mixing Pauli repulsive and molecular attractive exchange energies, and it can allow the unreal H3 and H4 molecules to form.
So physicists had to replace the conventional quantum mechanical method by the new ad-hoc molecular orbital (= MO ) theory.
But this molecular orbital (= MO ) theory artificially delocalizing each electron between atoms always generates the unrealistic ionized states ( this p.9 ) even in neutral molecular bonds (= in MO theory, two electrons of a neutral H2 molecule can unscientifically belong to only one hydrogen atom forming H2 → H- + H+ fictitious ions against Coulomb force ), hence, MO tends to unrealistically increase the total energies ( this p.27, this p.5-upper ).
Furthermore, the molecular orbital (= MO ) theory, where each molecular bond is independent of other molecular bonds, often fails in dealing with polyatomic molecules and various key bonds .
The molecular orbital (= MO ) theory failed ( this p.2-last ), because MO unfairly eliminates only molecular attractive exchange energies between two opposite spins, hence, MO can Not be used to explain important intermolecular attraction such as hydrogen bonds and van der Waals forces ( this p.2 ).
MO tries to eliminate the unneeded Pauli repulsion between different molecular orbitals by imposing the artificial rules of "orthoginal wavefunctions", but after all, the orthogonal wavefunctions cannot eliminate the unneeded Pauli repulsion, disproving MO.
So the failed molecular orbital (= MO ) theory gave up calculating molecular energies from the original quantum mechanical theory, and instead, introduced the empirical Huckel methods (= empirical means MO needs to adjust free-parameters based on experiments, Not on quantum mechanical theory ), which could treat only π double bond. ← No single σ bonds cannot be handled by Huckel MO theory due to the unneeded Pauli repulsion.
And this Huckel MO method has to rely on very rough approximation and artificial ad-hoc rule where all exchange (= or resonance, overlap ) integrals or energies except between closest atoms are forced to be zero ( this p.13, this p.12 ).
↑ Even the exchange energies between closest atoms are free parameters derived from experiments Not from quantum mechanics ( this p.14-upper ), which is why the molecular orbital hero = Huckel theory is called "semi-empirical".
The ordinary quantum mechanical methods, whose multi-electron Pauli antisymmetric wavefunctions failed and cannot distinguish different electrons, forced physicists to choose the more unrealistic density functional theory (= DFT ) unscientifically replacing actual many-electron molecules or materials by only one-pseudo-electron model which requires physicists to artificially choose fictitious effective potential energies ( this p.2 ).
The serious problem is the current most-widely-used one-pseudo-electron DFT completely contradicts the quantum mechanical Pauli antisymmetric wavefunctions which need the exchange of different electrons ( electron-1 ↔ electron-2 ).
So one-pseudo-electron DFT's fictitious kinetic energy cannot generate strong Pauli repulsion allegedly caused by exchanging different electrons, as shown in this. → DFT is wrong, too.
This unreasonable one-pseudo-DFT model dominates the current academia as a main culprit in preventing our real science and innovation forever.
Even if quantum mechanics just chooses fake trial wavefunctions or basis sets to seemingly get energy values (= instead of solving the unsolvable Schrödinger equations ) close to atomic or molecular covalent bond energies even by making up new ad-hoc concepts of exchange energies, these chosen wavefunctions did Not work in intermolecular non-covalent energies or Pauli repulsion, as shown in basis set superposition errors or something.
Quantum mechanical wavefunctions are basically unable to explain the actual intermolecular interactions such as van der Waals attraction and Pauli repulsion without relying on artificially-introduced models with many freely-adjustable parameters and the temporary fluctuating classical electric dipole charge irrelevant to the original quantum mechanics.
Intermolecular energies are known to obey empirically-obtained Lennard-Jones potential relation (= Not obtained from quantum mechanical theory ) where repulsive energy proportional to 1/r12 (= r is intermolecular distance ) is Pauli repulsion and attractive energy proportional to 1/r6 is van der Waals interaction.
These coefficients and parameters must be artificially adjusted to experimental values ( this p.5 ). ← Quantum mechanics can Not predict any intermolecular van der Waals attraction or Pauli repulsion.
The long-range van der Waals attraction (~1/r6) is said to follow London dispersion interaction with atomic dipole polarizability parameters, while the short-range strong Pauli repulsion relation (~ 1/r12 ) with No theoretical justification can Not be obtained by any quantum mechanical methods ( this p.2, this p.1, this p.11 ).
Because if quantum mechanical wavefunction is true, the energy relations of Pauli repulsion (and van der Waals attraction ) must change exponentially (= instead of 1/r12 or 1/r6 ) and much more slowly at close range than the actually-observed acute change of Pauli repulsion ( this p.3, this p.2-right, p.3-Fig.2 ).
In fact, van der Waals attraction, which is allegedly caused by the uncertain instantaneous electric dipole resulting from some electron's charge fluctuation, has Nothing to do with the original quantum mechanical Schrödinger equation's prediction, either ( this p.16-right-lower~p.17 ).
The weak intermolecular van der Waals attraction can be naturally thought to be generated by the ordinary Coulomb electric attraction between classical electron charges fluctuating and moving around each nucleus of two molecules generating electric dipole.
Quantum mechanical unphysical wavefunction or electron cloud, which must be always symmetrically distributed around each atomic nucleus, can Not generate Coulomb electric attraction between two neutral atoms or molecules contrary to the experimental facts.
↑ In order to generate Coulomb attraction between two neutral atoms by displacing the whole wavefunction from the original symmetrical position, quantum mechanics needs unrealistically-large energy exceeding the original ground state energies (= Quantum mechanical molecular attraction between unphysical electron spherical clouds is originally due to penetration and illegitimately lowered kinetic energy causing paradoxical bond strength, Not due to the realistic electrons moving, fluctuating and avoiding other electrons ).
Quantum mechanical static wavefunction and spreading electron cloud fails to explain actual non-covalent ( or covalent ) bonds, so in order to get the London's van der Waals attractive energy relation, quantum mechanics has to artificially introduce the ad-hoc randomly-fluctuating dipole electric pseudo-model with freely-adjustable parameters and the imaginary atomic frequency ω ( this p.17, this p.4, this p.6-7 (or p.16-17), this p.2-left p.19-left, this p.3-right ).
It means as the result of physicists unrealistically trying to obtain this originally-classical electric dipole-dipole van der Waals attraction by the unphysical quantum mechanics ( this p.7-right-lower ), they have to invent new ad-hoc artificial concepts called "time-dependently instantaneously- fluctuating electric dipole potential energy" allegedly governed by the unreal imaginary frequency and other adjustable dipole-charge parameters ( this p.6, this p.2 ).
↑ Each time physicists face the cases contradicting quantum mechanics (= van der Waals attraction or Pauli repulsion ), they artificially invented ad-hoc new fictional models, concepts and free parameters, which fact clearly shows the quantum mechanical inherent inability to predict any physical values.
As a gold-standard time-consuming method for explaining this invisible "imaginary fluctuating dipole", quantum mechanics often uses the rough artificial approximate model called the time-dependent coupled cluster (= CCSD = against the authentic quantum mechanical variational method, so false ) where physicists have to choose "fictitiously-excited wavefunctions" or basis sets ( this 5th-paragraph ) to generate the artificial temporarily polarized atoms by hand ( this p.1-2. )
Intermolecular van der Waals attraction is caused by the fluctuating moving electrons' dipole charges, which contradict the original quantum mechanical static wavefunctions where electrons are Not actually moving ( this 2nd paragraph ) despite their kinetic energies.
In order to describe this convenient 'temporarily-fluctuating' electron charge in van der Waals attraction, quantum mechanics has to artificially excite electrons against intraatomic Coulomb attraction by increasing energies, which forced physicists to rely on the ad-hoc time dependent coupled-cluster approximate model (= CC or TD-CCSD, this p.2 ), which is Not the authentic quantum mechanical variational method originally persuing the lowest ground state energy ( this p.8-top, this p.24 or p.44, this p.1-left-last-paragraph ), hence wrong with No power to predict any physical values due to its artificial adjustment of excited-energy free parameters ( this p.10 ).
Due to quantum mechanical inability to predict physical values, physicists had to invent various fictitious intermolecular potential energy equations such as Lennard-Jones, Morse, and Buckingham potentials.
Morse potential energy curve can be obtained by artificially fitting several parameters to experimental values, which has nothing to do with quantum mechanical prediction based on Schrödinger equations.
Because physicists need to know the equilibrium intermolecular distance (= r0, or the lowest energy point ) from the experiments, which can Not be derived by quantum mechanical calculation based on Schrödinger equations summing up Pauli repulsion (= with No theoretical justification ) and van der Waals attaction ( this p.11-lower ).
And there are many cases where this artificially-created Morse potential curve with fitting parameters failed to explain actual intermolecular energies ( this p.2-1st-paragraph ).
Other intermolecular pseudo-potential model called "Buckinghanm potential" replacing the actually-strong Pauli repulsion (= only at short range ) proportional to 1/r12 by weak exponential forms (= by adjusting parameters Not by quantum mechanical theory ), which causes unrealistically strong van der Waals attraction, hence a false model.
↑ Buckinghanm pseudo-potential causes unrealistically too low van der Waals energy at close range r ( unlike the ordinary Lennard Jones' potential ) called "Buckingham catastrophie" disagreeing with experimental facts ( this middle Buckingham potential section ).
Impractical quantum mechanics had no choice but to regress (= instead of progress ) to very primitive unscientific approximation called density functional theory (= DFT or Kohn-Sham theory ) which unreasonably replaces all multi-electron atoms and molecules by one-pseudo-electron model with fictitious kinetic energy ( this p.2 ) and unknown pseudo-potential called exchange correlation functional ( this p.3, this p.27 ).
Replacing the original multi-electron Schrödinger equations containing multiple different electrons' coordinates or variables (= r1, r2, r3 ... rN ) by only one single pseudo-electron's variable (= r ) means DFT is intrinsically unable to describe actual physical phenomena involving many differently moving electrons and atoms needing many different electrons' variables or coordinates representing the independently-changing positions of different moving electrons.
DFT with only one pseudo-electron's variable clearly can Not describe quantum mechanical Pauli repulsion expressed by antisymmetric wavefunctions where exchanging two different electrons' variables flips the sign of the entire multi-electron wavefunction ( this p.7-8 ).
↑ If the wavefunction contains only one electron's variable like DFT ( this p.12 ), exchanging two different variables to cause Pauli principle itself is impossible.
Quantum mechanical Pauli antisymmetric rule.
wavefunction = ψ( r1, r2 ) = - ψ( r2, r1 ) ← Wavefunction ψ flips its sign by two different electrons' exchange r1 ↔ r2 = Pauli antisymmetric.
But in the currently most widely used DFT model with only one single pseudo-electron or one variable (= r )
antisymmetric wavefunction = ψ( r, r ) = - ψ( r, r ) → 2 ψ( r, r ) = 0 → ψ( r, r ) = 0 ← total wavefunction ψ(r) becomes zero, if it satisfies Pauli antisymmetric wavefunction !
So the most popular density functional theory or DFT with only one pseudo-electron model contradicts the original quantum mechanics.
DFT is also unable to explain the ordinary van der Waals attraction ( this p.7, this p.1-right-upper ) without adding ad-hoc new pseudo-potential by destroying and changing the original Schrödinger equation's potential ( this p.12, this (10) ).
Of course, one-electron DFT wavefunction has No physical meaning ( this p.5, this last paragraph. ) causing unrealistic self-interacting energies (= due to one pseudo-electron repeling itself by Coulomb repulsion, which must be corrected by adding ad-hoc pseudo-potential exchange correlation energies ).
The recent Deepmind's alphafold team tried to predict protein structures from the experimentally-obtained protein structure database (= PDB ), Not from the useless quantum mechanics.
But Deepmind AI looking only at protein structure database, which did Not consider the actual electron's interactions at all, cannot predict protein interactions or chemical reactions. ← the drug development considering chemical reactions between drug molecule and target proteins, viruses, cancers is still impossible in Deepmind.
This article (p.2-right) says
"The network’s reliance on information
about related protein sequences means that
AlphaFold has some limitations. It is not
designed to predict the effect of mutations,
such as those that cause disease, on a protein’s shape. Nor was it trained to determine
how proteins change shape in the presence of
other interacting proteins, or molecules such
as drugs."
Under the present dead-end fantasy quantum mechanics, all Deepmind AI could do was rely on one-pseudo-electron approximation = DFT to seemingly explain some electron's behavior, because this one-pseudo-electron DFT is the present only quantum mechanical approximate method for large molecules, hence, DFT is a main culprit in preventing the current applied scientific developmnet.
As I said, it is intrinsically impossible to describe actual many-electron physical phenomena (= governed by many independent electrons' variables or coordinates ) by the only- one pseudo-electron DFT model (= containing only one independent variable ) and fictitious potential called exchange correlation functional which exact form is still (= and forever ) unknown ( this 2nd-paragraph ).
Deepmind or machine-learning tried to modify the current most popular fictitious one-pseudo-electron exchange functional called B3LYP using empirically-fitted parameters ( this p.24-25 (= or sup-S1 ), this Fig.2, this p.2-left ). ← The use of empirically-adjustable parameters means this has nothing to do with quantum mechanical prediction.
One-pseudo-electron DFT model has to find the still-unknown universally-exact fictitious exchange correlation functional (= which is impossible forever, this p.1-right, this p.21, this p.6-8 ).
Actually, Deepmind's new exchange potential functional failed to explain other physical phenomena ( this 8th-last-6th-last paragraphs ) even now.
↑ Finding the (non-existent) universally-exact one-pseudo-electron exchange potential and kinetic energy functional for DFT is an impossible dream forever, which wasted effort and time for pursuing the non-existent universal pseudo-potential = exchange-correlation functional just stops our real science from progressing.
(Fig.2) The opposite (or same ) spins cause the symmetric molecular attraction (or antisymmetric Pauli repulsion ) ? Heitler-London (= HL ) and molecular orbital (= MO ) methods
Pauli repulsion or Pauli exclusion principle is the important force in our daily life, which explains why we cannot penetrate a rigid object by stopping two molecules from approaching using mysterious repulsive force ( this p.2 ).
But unrealistic quantum mechanics obstinately refuses to admit this actually-measurable Pauli repulsion to be a real force or a real thing ( this p.6, this p.4-middle ).
Quantum mechanics just mentions that Pauli principle results from (nonphysical) antisymmetric wavefunctions. ← No more detailed explanation was given by quantum mechanics !
According to this quantum mechanical ad-hoc unphysical antisymmetric rule, exchanging any two electrons (or electrons' coordinates r1 ↔ r2, r2 ↔ r3, r1 ↔ r3 ) must flip the sign of the entire wavefunction like ψ( r1, r2 ) → - ψ( r2, r1 ) when r1 ↔ r2.
So when two electrons exit in the same state or same wavefunction, the entire antisymmetric wavefunction becomes zero like antisymmetric wavefunction = φ(r1)ψ(r2)-ψ(r1)φ(r2) → when φ = ψ → φ(r1)φ(r2)-φ(r1)φ(r2) = 0. ← Pauli repulsion ? ← No more detailed explanation exists in quantum mechanics except this too abstract unphysical antisymmetric rule ! No wonder our science stops progressing now.
Th entire wavefunction is supposed to be separated into spatial and spin parts. ( this 8.6.6-8.6.11, this p.14-18, this p.4 )
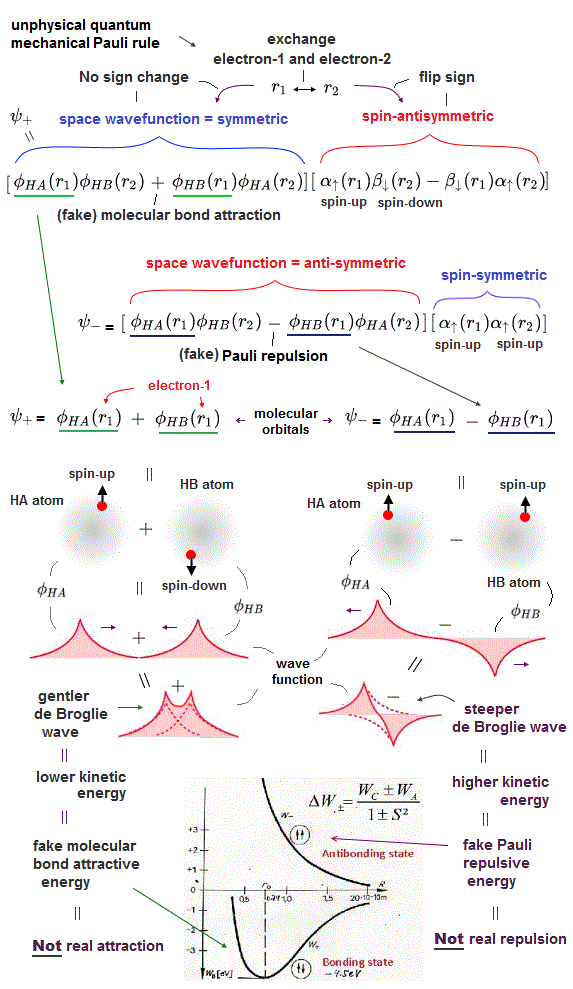
For example, in hydrogen molecule (= H2), when two electrons of two hydrogen (= H ) atoms have the same symmetric spins (= parallel spins or triplet ), the spatial wavefunction must take antisymmetric form, which allegedly generates Pauli repulsion between two electrons with the same spin and stops two atoms from approaching by increasing total energy called antibonding ( this lower ).
When two electrons of two H atoms have the opposite antisymmetric spins (= antiparallel spins or singlet ), the spatial wavefunction must take symmetric form (= hence, the entire wavefunction = spin antisymmetric × spacial symmetric = antisymmetric satisfying Pauli principle rule ), which allegedly causes fictitious molecular bond attractive energy by lowering total energy.
These antisymmetric or symmetric molecular spatial wavefunctions cause nonphysical exchange integral or exchange energies which generate Pauli-repulsive antibond or molecular attractive bond depending on the sign connecting two terms of exchanged coordinates.
These exchange energies are Not real forces or things ( this p.2-left-lower, this p.5 ).
In order to cause this nonphysical exchange integral or exchange energies which allegedly account for molecular Pauli repulsive and attractive bond energies, each single electron must unrealistically exist in two separate atoms and orbitals simultaneously ( this p.11, this p.28 ) as shown in the antisymmetric wavefunctions ( this p.3 ).
↑ H2 molecular wavefunction must include two kinds of H-atomic wavefunction = φHA(r1) and φHB(r1) with respect to the electron-1 or r1 ( this p.14 ), and also include φHA(r2) and φHB(r2) with respect to the electron-2. ← A single H2 molecule must include 4 different H atomic wavefunctions simultaneously, using quantum mechanical unrealistic parallel worlds or superposition.
What's the origin of this mysterious Pauli repulsive and molecular attractive energies ?
When the spatial wavefunction is symmetric = φHB(r2)φHA(r1) + φHB(r1)φHA(r2), the electron-1's wavefunction's part becomes the sum (= + ) of two HA and HB atomic wavefunctions like
φHA(r1) + φHB(r1). ← molecular attractive bond.
↑ These two wavefunctions symmetric with each other cause constructive interference, enhance (wavefunction) amplitude, and make the slope of the entire overlapped wavefunctions more gentle ( this p.4 ).
Quantum mechanical Schrödinger equation also uses de Broglie wave theory.
So the constructively-interfering wavefunction with more gentle slope (= smaller curvature ) elongates its de Broglie wavelength (= λ ) which means the decrease in the electron's momentum (= p = h/λ ), hence, it decreases electron's kinetic energy.
↑ This fictitious exchange energy based on the decreased (pseudo-)kinetic energy (= lowering total energy, too ) is said to be the origin of quantum mechanical fictitious molecular bond attractive energies.
↑ The real attraction should be generated by lower potential energy, Not by pseudo-kinetic energy decrease (= if real molecular attraction exists, the attraction usually pulls the electron and increases electron's kinetic energy ! ), so this quantum mechanical exchange energy contradicts basic physical principle.
This quantum mechanical attractive exchange energies based on decreased kinetic energies are unrealistic (= with No physical meaning ), because in the realistic world, it's impossible to decrease only electrons' kinetic energies without any real force or potential change acting on electrons, and this exchange energy violates the total energy conservation law, though the total energy E must be always conserved also for quantum mechanics to solve Schrödinger equations.
So quantum mechanics violating energy conservation law to generate fictitious exchange energies is proved to be contradictory and false.
When the entire spacial wavefunction is antisymmetric = φHA(r1)φHA (r1) - φHB(r1)φHA(r2) (= Heitler-London or valence bond notation ), the electron-1's wavefunction's part becomes the "subtraction" (= - ) of one HB atomic wavefunction from the other HA wavefunction like
φHA(r1) - φHB(r1). ← antibond or Pauli repulsion (= molecular orbital or MO notation ).
The subtraction of one wavefunction from the other wavefunction means destructive interference which makes the slope of the the entire wavefrunction steeper, shortens de Broglie wavelength and increases the electron's kinetic energy and total energy as antibond.
This is why quantum mechanics claims the strong Pauli repulsion originates from the unphysical exchange energies caused by the increased kinetic energies ( this p.2-3rd-paragraph, this p.3-left ) by the unphysical destructively-interfering antisymmetric wavefunction.
↑ Again, this quantum mechanical Pauli repulsion based on kinetic energy increase is against the basic principle where repulsion usually pushes back and slows down the electron (= hence, real repulsion should decrease (= Not increase ) the electron's kinetic energy ) !
What causes this magically increased or decreased kinetic energies is unknown, this is why quantum mechanics ridiculously claims Pauli exchange repulsion is Not a real force ( this p.9-10, this p.2-left-lower ), though Pauli repulsion is actually measurable. ← self-contradiction.
(Fig.3) ↓ Pauli repulsion disappears in three electrons !?

In fact, quantum mechanical Pauli principle based on antisymmetric wavefunctions is invalid in more than two electrons, so quantum mechanics is wrong.
When there are only two electrons ( 1 and 2 ) with the same spins, their unphysical antisymmetric wavefunction (= φB(2)φA(1) - φB(1)φA (2) = φA(1) - φB(1) ) destructively interferes (= steeper wavefunction increases fictitious kinetic energy ) and causes Pauli repulsive energy expressed as minus exchange energy or the antibond repulsively higher energy ( this p.3 ).
↑ A single electron-1 must exist in two different atomic nuclei A and B simultaneously to cause destructive interference ( this p.3-4 ), or overlap exchange integral = ∫ φA(1)φB(1) dv1 ( this p.6, this p.4, this p.7 ).
But in cases of more than two electrons with the same spin, this quantum mechanical artificial rule expressing Pauli repulsion as antisymmetric wavefunction collapses and becomes invalid.
When there are three electrons with the same spin, the entire wavefunction must take antisymmetric forms where exchanging any two electrons flips the sign of the entire wavefunction as shown in Slater determinant ( this p.7 ).
In the upper figure, when the electron-1 existing in atom-A wavefunction (= φA(1) ) interferes with the electron-1 itself also existing in atom-B wavefunction (= φB(1) ) generating the unphysical exchange integral (= -∫ φA(1)φB(1) dv1 ) or exchange energies ( this p.11 ), there are two φB(1) wavefunction terms with the opposite signs (= ±φB(1) ) which cancel each other (= one is destructive, the other is constructive interference between φA(1) and ±φB(1) ) and become zero. → No Pauli repulsive exchange integral !
↑ This is the fatal flaw of quantum mechanical antisymmetric Pauli repulsion rule which becomes invalid by canceling Pauli exchange energies, when there are more than two electrons ( this p.20 ).
Of course, there are much more than two electrons in this world ! So quantum mechanics is false.
In the upper figure, three electrons's antisymmetric wavefunction expressed as 3 × 3 determinant includes - φA(2)φB(1)φC(3), and +φA(3)φB(1)φC(2) = - φB(1) + φB(1) = 0
↑ Coefficients φA(2)φC(3) and φA(3)φC(2) are symmetric with respect to 2 ↔ 3, hence, if we consider the superposition of all places of electrons-2 and 3, these two coefficients just become the same, and the above two terms cancel each other to be zero. ← No Pauli repulsion occurs in quantum mechanical antisymmetric wavefunctions !
As shown in constructive and destructive interference of an electron in double slit experiments, quantum mechanics requires the probability wavefunctions in all possible electron's positions (= superposition ) to interfere with each other (= In the destructive interference area combining ±wavefunction, the electron's probability is canceled out to be zero ).
So we need to overlap or superimpose all wavefunctions of all electrons' posssible positions also in atomic antisymmetric probability wavefunctions, too. → Pauli repulsion disappears by the zero exchange integral !
↑ Quantum mechanical Pauli antisymmetric wavefunction rule contradicts the quantum mechanical basic principle of the double-slit interference of all the electron's superposition states, → The destructive interference between Pauli repulsion (= minus exchange energy ) and the fictitious molecular attraction (= positive exchange integral = ± opposite sign in above figure ) cancels them, and Pauli repulsion disappears, hence, quantum mechanical Pauli principle is wrong.
Actually, this integral of antisymmetric wavefunctions square the entire wavefunction amplitude before summing up all electrons' positions' superposition states in the original isolated wavefunction amplitude, hence, coefficients of the above two terms are different and don't cancel each other.
↑ When squaring the upper antisymmetric wavefunction and comparing two coefficients of exchange integral ± ∫ φA(1)φB(1), one coefficient becomes -φB(2)φA(2)[φC(3)]2 (= overlap integral = S with electron-2 × the normal probability integral = 1 with electron-3 ) and the other coefficient becomes +φB(2)φC(2) φC(3)φA(3) (= two overlap integrals = S2 with both electrons-2,3 ). ← Overlap integral S is smaller than 1, hence, the minus coefficient -φB(2)φA(2)[φC(3)]2 of the exchange integral ∫ φA(1)φB(1) is more dominant, and minus exchange integral causing Pauli repulsion can occur in this case.
↑ But this quantum mechanical probability integral or squaring wavefunction amplitudes before all superposition wavefunctions interfere destructively and become zero is inconsistent with the original quantum mechanical double-slit interference rule, so wrong.
If the original quantum mechanical superposition interference rule is right, all the antisymmetric wavefunctions of more than two electrons becomes canceled out to be zero and flattened, hence, electron's kinetic energy expressed by the wavefunction slope becomes zero, and Pauli repulsive energy is gone.
This integral of the squared wavefunctions before summing up all the wavefunction amplitudes contradicts the original quantum mechanical double-slit interference principle (→ the entire antisymmetric wavefunctions always should be zero in the above 3 × 3 antisymmetric wavefunction by destructive interference, if the double-slit interference rule summing up all wavefunction amplitudes before squaring the wavefunction is used ).
As a result, quantum mechanical Pauli antisymmetric wavefunctions do Not apply to the cases containing more than two electrons, hence, quantum mechanics is false.
Of course, the current most-widely used one-pseudo-electron DFT cannot utilize this Pauli antisymmetric wavefunctions expressed by exchanging multiple different electrons' coordinates, so DFT's wavefunction amplitude always becomes zero and Pauli principle is invalid, if we try to apply antisymmetric rule in DFT.
↑ In this original Pauli antisymmetric wavefunctions using three different electrons expressed by three variables (= r1, r2, r3 ), each electron's wavefunction amplitude changes depending on the other two electrons' variable values, so when these electrons' variables take different positions or values, each electron's wavefunction amplitude magically changes from minus to plus amplitute even at the same place depending on other different electrons' coordinates or positions (= one pseudo-electron DFT cannot use this multi-electron trick ).
Using this illegitimate trick, this antisymmetric wavefunction artificially creates destructive and non-destructive interference patterns between different electrons alternately depending on different valuables' values (= originally, adding up all these changing values and amplitudes should make all places' amplitudes zero, though ) in the same originally-zero amplitude place.
↑ If we add up all these changing amplitudes at each place, all of these wavefunction amplitudes are just canceled out to be zero. ← The flattened wavefunction amplitude generates No kinetic energy → No Pauli repulsion when there are more than two electrons !
But as I said, they square the wavefunction amplitude before adding up the all wavefunction amplitudes to deliberately avoid destructive interference in the originally-zero wavefunction amplitude area and paradox, which trick clearly contradicts the original double-slit interference rule adding up all possible wavefunction amplitudes as "interference" before squaring them.
The most serious fatal flaw is these quantum mechanical Pauli antisymmetric wavefunctions can Not express the mixed states of Pauli repulsive (= antisymmetric or flipping the entire sign by exchanging two electrons with the same spin ) and molecular attractive (= symmetric or the unchanged sign by exchanging two electrons with the opposite spins ) exchange energies.
↑ Even if you try to artificially make the mixed chimera wavefunctions combining the antisymmetric (= between two electrons with the same spin ) and symmetric (= between two electrons with the opposite spins ) wavefunctions, you will find these strangely-mixed wavefunctions are impossible to make.
According to quantum mechanics, all the actual atoms and molecules should mix two types of up and down spins, hence it needs the mixed wavefunctions incorporating the molecular bond symmetric (= between the opposite spins ) and Pauli repulsive antisymmetric (= between the same parallel spins ) wavefunctions at the same time, these indispensable mixed wavefunctions can Not be expressed by quantum mechanical Pauli antisymmetric wavefunctions !
So quantum mechanical Pauli antisymmetric or molecular symmetric wavefunctions exchanging muli-electrons completely failed, and this failure led physicists to give up the multi-electron Schrödinger, Hartree-Fock equations or ad-hoc molecular orbital theory, and reluctantly choose the unrealistic one-pseudo-electron density functional theory or DFT to hide the intrinsic failure of quantum mechanics by the unknown pseudo-potential energy called exchange-correlation functionals.
Pauli antisymmetric wavefunctions are based on exchanging multiple different electrons unlike one-pseudo-electron DFT.
So in the current most-widely-used one-pseudo-electron DFT (= using only one variable r ), the Pauli antisymemtric wavefunction's trick of changing destructive interference states at the same place depending on other different electrtons' variables cannot be used, so the total antisymmetric wavefunctions always become zero in DFT, and DFT should be unable to use Pauli antisymmetric wavefunction's repulsion.
↑ One pseudo-electron DFT tries to use multiple different fictitious non-interacting independent kinetic energies by unreasonablly breaking one pseudo-electron (= expressed by only one variable ) into multiple fictitious independent sub-wavefunctions (= all of which sub-wavefunctions share only one variable, but paradoxically independent of each other ! ), which is inconsistent and does Not work.
(Fig.4) Pauli "repulsion" between electrons of the same up-spin becomes "attraction" when there are more than two electrons !?
Quantum mechanics states that Pauli exclusion repulsion is caused by antisymmetric wavefunctions which must change the sign under the exchange of any two electrons (= any possible exchange of any two electrons' coordinates or variables should flip the sign of the entire wavefunction like ψ(1,2) = - ψ(2,1), ψ(2,3) = - ψ(3,2) .. )
In fact, this quantum mechanical Pauli repulsion allegedly generated by unphysical antisymmetric wavefunctions is invalid when there are more than two electrons, if quantum mechanical interference is considered in the right way.
Quantum mechanics insists two electrons with the same-directional (ex. up-up ) spin repel each other by strong Pauli repulsion, and forbids them from entering the same place or state.
The problem is unphysical quantum mechanics cannot treat this actually-measurable Pauli repulsion as real forces, just using the confusing word "exchange interaction".
Quantum mechanics says when there are two electrons with the same (up) spin (= spin-symmetric or triplet ), the total wavefunction takes an antisymmetric form where two atomic wavefunctions with the opposite phases interfere destructively, making the slope of the wavefunction steeper, increasing the kinetinc energy, which allegedly causes Pauli repulsive antibond and stops two molecules from approaching ( this p.3 ).
↑ This quantum mechanical Pauli repulsive mechanism is paradoxical and self-contradictory, so wrong.
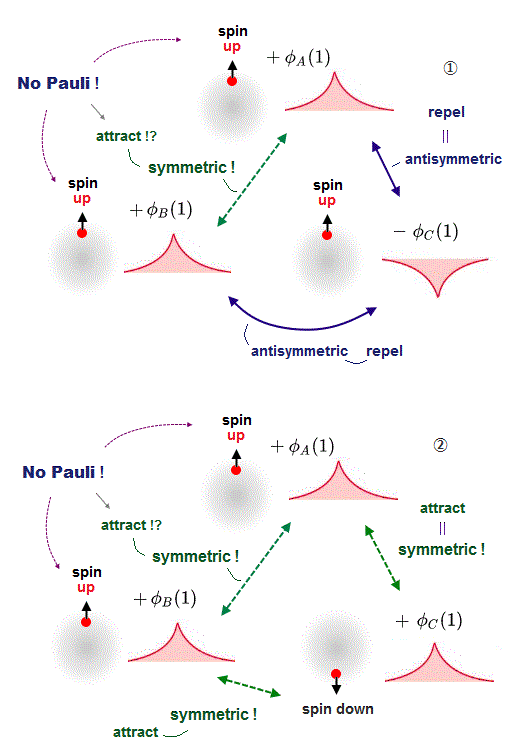
In the upper figure, when there are three electrons with the same up spin, Pauli repulsion must be generated among all these three electrons with the same up-spin.
As I said, in order to generate Pauli repulsion between two electrons, one electron's wavefunction becomes minus phase (= - φC in the upper figure ), and other electrons must have the positive phase (= +φA and +φB in the upper figure ).
↑ In this case, the wavefunctions between -φC and +φA, -φC and +φB becomes steeper increasing Pauli repulsive energy by destructive interference.
But if so, both the wavefunctions +φA and +φB become the same positive symmetric phase and cause attractive constructive interference as if they had the opposite spins, though they actually have the same spin !
↑ This is clearly a paradox, so quantum mechanical Pauli mechanism is unscientific and false.
Quantum mechanics states only when two electrons have the opposite up-down spins (= spin-anti-symmetric or singlet ), these two electrons' spatial wavefunctions become the same + phase symmetric form, and cause the constructive interference, making the total wavefunction's slope gentler, decreasing kinetic energies contributing to molecular bond attraction.
When the wavefunction φC has the down spin and other φA and φB wavefunctions have the opposite up spin, all these three wavefunctions must become the same positive phase (= symmetric or constructive interference ) to cause molecular bond attraction between φC (= down spin ) and other two φA (= up spin ), φB (= up spin ).
But in this case, two wavefunctions φA (= up spin ), φB (= up spin ) have the same positive phase, hence, cause constructive interference and molecular bond attraction between A and B, though A and B have the same up spins (= electrons with the same spin must repel each other by destructive interference ! ).
These cases are clearly fatal paradoxes of quantum mechanical Pauli principle mechanism allegedly caused by the spin direction-related (anti)symmetric wavefunctions.
Actually, quantum mechanical Pauli antisymmetric wavefunctions cannot describe multi-electron molecules mixing spins up and down. = Quantum mechanics is unable to describe the actual wavefunctions mixing molecular attractive bond symmetric (= between the opposite spins ) and Pauli antisymmetric (= between the same spins ) wavefunctions, so impractical and wrong.
Molecular orbital (= MO ) theory also uses this molecular bond attractive symmetric (= constructive interference ) and Pauli repulsive antisymmetric (= destructive interference or antibond ) exchange energies based on spins.
In addition to various paradoxes of ad-hoc MO theory, the Huckel theory representing this MO theory illegitimately avoids considering all exchange (= resonance ) energies or integrals except between the nearest neighboring atoms to hide this paradox ( this p.15, this p.12 ).
(Fig.5) Quantum mechanical Pauli principle is false.
In fact, quantum mechanical Pauli repulsion expressed as unphysical antisymmetric wavefunction is so weak that it cannot block three or four hydrogen atoms from forming unreal H3 or H4 molecule, so quantum mechanics based on molecular attractive bond exchange and Pauli repulseive exchange energies is false (= the later ad-hoc molecular orbital theory eliminating this molecular bond attractive exchange energy and leaving only the unneeded Pauli repulsive exchange energy is false, too. ← So any quantum mechanical multi-electron models failed ).
According to quantum mechanics, two electrons with the opposite (= up and down ) spins can form molecular attractive bonds due to constructive interference of symmetric wavefunctions lowering total energies ( this p.4 ).
For example, quantum mechanics says a helium atom with two electrons of up and down spins cannot bind to another neighboring helium atom because the number of attractive bonds between spin-up and spin-down electrons becomes the same as the number of Pauli repulsive antibonds between spin-up and spin-up (or spin-down and spin-down ).
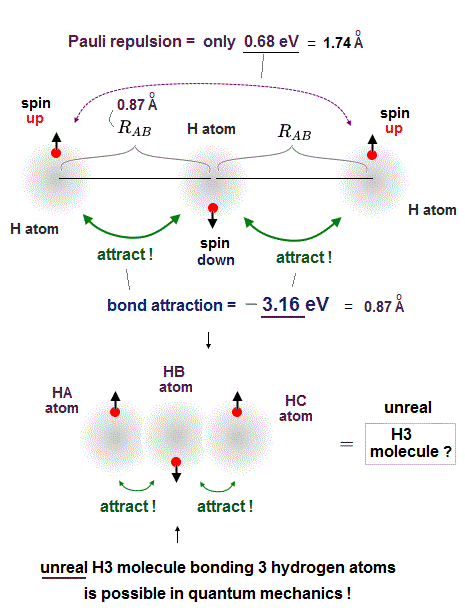
But a hydrogen atom (= H ) has only one electron with up or down spin, hence if two adjacent hydrogen atoms in two adjacent hydrogen molecules have different spins opposite to each other, two adjacent hydrogen molecules should bond to each other by strong attractive covalent bonds and form unreal H3 and H4 molecules containing more than two hydrogen atoms.
So when three hydrogen atomic electrons line up like spin-up, spin-down and spin-up as shown in the upper figure, two adjacent H atoms (= with spins opposite to each other ) can safely form the tight covalent attractive bond and unreal H3 molecule.
↑ This quantum mechanical molecular bond and Pauli repulsive mechanism based on up-down spins disagrees with the fact that both H2 molecule or He cannot form molecular bonds with another H2 molecule or He, as seen in extremely low boiling points (= almost absolute zero -270 K temperature ).
In order to block this unreal H3 molecular bonds, two electrons of two separate H atoms (= which are two atoms away from each other ) with the same up-up spin must repel each other strongly enough to block H3 molecular bonds by following the Pauli antisymmetric wavefunction rule ( this p.9 ).
The problem is the distance between these two separate electrons (= which are two H atoms away from each other ) with the same up-up spin on the left and right sides are far longer (= so Pauli repulsion is weaker ) than the distance between two adjacent atoms with the opposite spins (= molecular attractve bond between two electrons with the opposite spins becomes stronger ), so this Pauli repulsion is too weak to block unreal H3 formation.
As shown in this and this, the molecular attractive energies between two adjacent atoms separated by the distance RAB is far stronger than Pauli repulsive energy between two distant atoms (= two atoms apart from each other ) separated by longer 2 × RAB ( this p.5 ).
It is quite natural that attractive bond energy at closer distance becomes stronger than Pauli repulsion at twice longer distance, hence H2 molecule can naturally bond to another H atom to form non-existent H3 molecule according to quantum mechanics !
This means if quantum mechanical antisymmetric Pauli principle rule is right, unreal H3, H4, H5.. molecular covalent bonds are possible, disagreeing with the actual molecules !
We actually calculate molecular bond energy and Pauli repulsive energies between three hydrogen atoms and confirm this unreal H3 molecular formation is allowed by quantum mechanics later.
(Fig.6) Two electrons: φA with up-spin ↑ and φB with down-spin ↓ should form molecular attractive bonds, but Pauli antisymmetric rule forbids it !

In fact, quantum mechanical Pauli principle allegedly caused by antisymmetric wavefunctions has fatal flaws.
Pauli exclusion principle states that No two electrons can occupy the same state with respect to spin and orbitals.
So to occupy the same orbital, two electron must have the opposite spins different from each other.
And two electrons with the opposite up and down spins must contribute to forming attractive covalent bonds through attractive exchange energies generated by symmetric wavefunctions according to quantum mechanics ( this p.4 ).
↑ But in fact, if quantum mechanical Pauli antisymmetric wavefunction is true, this wavefunction cannot form normal molecular attractive covalent bonds due to automatically eliminating the attractive exchange energies or symmetric wavefunctions. → No molecules in quantum mechanical world !
In quantum mechanical antisymmetric wavefunction (= φA(1)φB(2) - φA(2)φB(1) ) equal to Slater's determimant expression, when two wavefunctions (= with respect to spin and orbital ) are completely the same (= φA = φB ), the entire antisymmetric wavefunction becomes zero, which condition is required for Pauli principle.
Antisymmetric wavefunction = φA(1)φB(2) - φA(2)φB(1) = φA(1)φA(2) - φA(2)φA(1) = 0 ← zero, when φA = φB (= A and B have the same spin and orbital ).
↑ Pauli mentioned No more detailed mechanism of how mysterious Pauli repulsion is generated than this very abstract unphysical antisymmetric wavefunction rule ( this p.3 ).
So in the Pauli antisymmetric wavefunctions, each wavefunction must consist of spin (= up-spin ↑ = α down-spin ↓ = β ) and spacial parts ( this p.2-3, this lower ).
Hence, the official antisymmetric wavefunction with φA having up-spin and φB having down-spin becomes
ψ = φA(1)↑(1) φB(2)↓(2) - φA(2)↑(2) φB(1)↓(1). ← These two terms are 1 ↔ 2
To calculate energies, we need to square this antisymmetric wavefunction, integrate it and generate the exchange integral for molecular attractive bond energies. The squared antisymmetic wavefunction (= ∫ ψψ ) becomes like the upper figure.
In this case using antisymmetric wavefunctions, the exchange integral terms always become zero, and only the useless Coulomb energy terms remain, when we consider two electrons with the opposite spins in antisymmetric wavefunctions ( this-(18.2.5) ). ← Only unneeded Pauli repulsive exchange energies between the same up-up or down-down spins remain ( this p.29-30, this p.10-11, this p.5, this p.44-lower ).
Because the exchange integral of two electrons with the opposite up-down spins always consists of the product of two different up and down spins in each electron-1 ( and 2 ) wavefunction like,
Exchange integral of electron-1 part = ∫φA(1)↑(1) φB(1)↓(1).
Integration of the product of two different up and down spins with respect to spin variable always becomes zero ( this p.13, this p.10 ) like
∫ ↑(1)↓(1) = 0 ← zero.
So the exchange integral part becomes always zero when two electrons have the opposite spins ( this p.20 ) ! → No molecular attractive exchange energy !
This is a serious problem, because quantum mechanics originally needs (unphysical) exchange energy excpressed by exchange integral as a major source of molecular attractive bond energies, while normal Coulomb energy expressed by Coulomb integral cannot generate enough molecular bond energies ( this p.3-4, this p.11, this lower-Fig.2 ).
Quantum mechanical unphysical exchange energy can utilize the "cheating" of lowering kinetic energies by violating energy conservation law. ← This "cheating" exchange energiy, which is the only driving force of quantum mechanical molecular bond energy, is gone in the quantum mechanical Pauli antisymmetric wavefunctions represented by Slatar determinants.
As a result, quantum mechanical Pauli antisymmetric wavefunctions are intrincically unable to explain strong molecular attractive bond energies such as H2 molecule due to its inability to ulitize attractive (positive) exchange integral or energies ( this p.5-6 explaining it in detail ).
Pauli antisymmetric wavefunction can only give Pauli repulstive exchange energies because the exchange integral doesn't disappear when two electrons have the same spin (= which means the spatial wavefunction becomes antisymmetric causing Pauli repulsion, this p.10-lower ) where integral of the same spin becomes 1 like
∫ ↑(1)↑(1) = ∫ ↓(1)↓(1) = 1
Textbooks often use wrong form of antisymmetric wavefunction with the opposite antisymmetric or singlet spins (= α(1)β(2) - α(2)β(1) ) This form does Not satisfy the original Pauli antisymmetric wavefunction expressed by Slater determinant.
Only when two electrons have exactly the same spatial orbital (= φA = φB ), this antisymmetric Slater determinant wavefunctions are equal to this form ( this 8.6.3 and 8.6.4 ).
In case of molecular bonds like H2 molecule, two hydrogen atomic wavefunctions φA and φB are different (= due to different nuclear positions ), so Pauli antisymmetric wavefunctions can Not generate molecular bond attractive exchange integral and energies.
This important fact is often ignored in almost all textbooks, but this inherent flaws of quantum mechanical Pauli antisymmetric rule forced physicists to completely change their ways to describe molecular bonds from the conventional valence bond (= Heitler-London ) method to the current mainstream molecular orbital (= MO ) methods ( this p.4, this p.6-8 ).
So physicists were forced to give up the original quantum mechanical wavefunction, and artificially create the ad-hoc molecular orbital (= MO ) theory where each electron must unrealistically spread in several different atomic and molecular orbitals simultaneously, which linear superposition wavefunction allegedly generates the controlled-form of molecular attractive or Pauli repulsive exchange energies.
And the uncontrolled and unneeded Pauli repulsion among different molecular orbitals must be zero by imposing the artificial rule called "orthogonal (or orthonormal, this p.5-lower ) orbitals" where exchange (or overlap ) energies or integrals among different orbitals must be zero ( this p.14, this p.1, this p.2, this p.15 ).
Actually, it's impossible to make the mixed wavefunction consisting of one spin-down (= φA ) wavefunction and two spin-up-up (= φB, φC ) wavefunctions where exchanging the same spin-up-up (= φB ↔ φC ) should be antisymmetric (= flip the sign of the entire wavefunction ), and exchanging different up-down spins (= φA ↔ φB, φC ) should be symmetric (= the entire wavefunction's sign is unchanged ).
Heitler made a failed attempt to generalize his antisymmetric wavefunctions to describe multiple atoms and bonds even by relying on artificial rules, restrictions and approximations ( this p.7-right-lower or p.9 ).
↑ This fact clearly disproves the quantum mechanical Pauli principle based on antisymmetric wavefunctions allegedly expressing repulsions and symmetric wavefunctions expressing molecular attractions.
Ad-hoc molecular orbital (= MO ) theory includes fatal flaws, so only the unrealistic one-pseudo-electron DFT is left to fictitiously express the mixed state of Pauli repulsion and molecular attraction, though one-pseudo-electron DFT clearly contradicts the original Pauli antisymmetric wavefunctions which need exchanging multiple different electrons, and DFT includes new fatal flaws, so false.
(Fig.7) MO replaced isolated atoms by fictitious molecular orbitals.

As I said, quantum mechanical Pauli antisymmetric wavefunctions cannot generate actual molecular attractive bond (exchange) energies which should occur between electrons with the opposite spin.
Because in Pauli antisymmetric wavefunctions or Slater's determimants, exchange energy integral, which accounts for a major portion of (fictitious) molecular bond energies, vanishes when electrons have the opposite up and down singlet spins ( this p.5-6, this p.10-lower )
So physicists needed to artificially create the vanishing exchange energy integral, which is necessary for molecular attractive exchange energy, in the originally-irrelevant Coulomb integral parts, which artificial new theory is the so-called molecular orbital (= MO ) theory, which is the second most popular theory after one-pseudo-electron DFT.
In the molecular orbital theory, each electron has to exist in the area between different atoms as σ or π bonds or Pauli repulsive antibonds from the beginning as linear combinations of isolated atoms ( this-(11.5.1) ). ← So molecular orbital theory cannot deal with the ordinary isolated atoms.
For example, in hydrogen molecular (= H2 ) bond, each electron belonging to each H atomic wavefunction must exist in the artificially-created bond (or antibond ) orbital between two H atoms, rather than belonging to each H atom like
φ+ = φA(1) + φB(1)
instead of each isolated H atomic φA(1) or φB(1) ( this p.7, this p.3, this p.9-last ).
So in this artificial MO theory, when squaring the wavefunction to obtain the probability or energy expectation values, it always generates unrealistic separate ions even in neutral molecules like H2 molecule → H+ positive + H- negative ions ( this p.9 ). ← MO unreasonably increases molecular total energies by this unrealistic ionization ( this p.27, this p.5-upper ).
↑ Normally, useless Coulomb energy integral parts contains ∫φA(1)φA(1) and the exchange term contains ∫φA(1)φB(1) which unphysical exchange integral part is the driving force of quantum mechanical molecular attractive bonds ( this p.18-20 ).
In this molecular orbital, the Coulomb integral (= the ordinary squared wavefunction, this p.9 ) automatically contains the originally-irrelevant exchange energy integral as shown in the upper figure ( this p.7, this p.8-9 ).
Coulomb integral of MO = ∫φ+φ+ = [ φA(1) + φB(1) ]^2 contains the exchange integral ∫ φA(1)φB(1) automatically ( this p.4-6 ), because MO theory uses the linear combination of two atomic wavefunctions instead of an isolated atomic wavefunction as a default wavefunction = φ+ = [φA(1) + φB(1)].
This ad-hoc trick causes various serious paradoxes and contradictions, which shows quantum mechanical Pauli principle and molecular orbital theory (= MO ) contain fundamentally fatal flaws.
The molecular orbital (= MO ) theory also uses constructive or destructive interference between electron wavefunctions as the origin of molecular attractive bond or Pauli repulsive exchange energies, so the MO causes fatal paradoxes and disagreement with experimental results inside the ad-hoc MO linear orbitals consisting of more than two electron wavefunctions in addition to its inherent unreal bonds.
This is the reason why in the MO's leading theory = Huckel model describing various carbon π bonds, physicists have to rely on ad-hoc empirical parameters (= artificially adjusted by experiments Not by useless quantum mechanics, this p.14-upper ) and very rough approximation where they outrageously ignores all exchange (= or resonance ) energies except between nearest neighboring electrons ( this p.13, this p.13 ) to avoid this fatal paradox forcibly.
Actually, the molecular orbital (= MO ) theory filled with so many paradoxes is Not so often used by physicists.
This defective MO theory is favored especially by chemistry textbooks as the only model to (misleadingly) visualize the nonphysical quantum mechanical atoms which originally lack physical images.
For example, according to the simple MO theory, a carbon's four valence electron orbitals ( = called sp3 ) are supposed to be in the superposition state of 2s±2px±2py±2pz to express the conveniently-beautiful tetrahedral structure of the carbon ( this p.5 ).
But in the actual MO theory, this simple tetrahedral carbon's four valence electrons cannot generate the bond energies of methane (= CH4 ), instead, physicists have to rely on empirically-obtained artificial parameters of Huckel CH4 model where each single hydrogen atom must be unrealistically divided and spread through all four C-H bonds ( this 5-7, this p.4-5 ).
(F.8) Reason why MO theory disagrees with actual molecules.
As I said in Fig.6, quantum mechanical Pauli antisymmetric wavefunctions expressed as Slater determinants consisting of spacial (= φ ) and spin parts (= ↑ or α = up-spin, ↓ or β = down-spin ) cannot generate actual molecular attractive exchange energies between up and down spins which pair should originally generate molecular bond attraction ( this p.5-6 ).
Because the molecular attractive exchange integral always includes the integral of spin-up and down which is always zero (= ∫ ↑↓ = ∫ αβ = 0, this p.19, this p.4 ).
In order to recover the vanished molecular attractive exchange energies, the ad-hoc molecular orbital (= MO ) theory was invented.
In the molecular orbital (= MO ) theory, each single electron is always expressed as a linear combination of several different atomic orbitals, hence the MO electron always contains the molecular attractive exchange energy as default ( this p.4-5, this p.8-9, which causes unreal ionized states in MO ) inside Coulomb integral, even if the original exchange integral unreasonably vanishes due to the zero spin integral of up and down opposite spins.
Th problem is while the molecular attractive exchange integrals between electrons with the opposite up-down spins always vanish, the Pauli repulsive exchange integrals between electrons with the same spin (= up-up or down-down, ∫ ↑↑ = ∫ ↓↓ = 1, Not zero ) never vanish.
So in MO, the intermolecular interactions always cause the unnecessary Pauli repulsive exchange energies (= this quantum mechanical fake antisymmetric Pauli repulsion between the same spins is not compatible with actually-observed Pauli repulsion pattern, though ).
Hence, MO can Not explain actual phenomena of the important intermolecular attraction such as hydrogen bond and van der Waals attraction without adding artificial models or pseudo-potential ( this p.2 ). ← MO theory is false.
Also in the MO theory, Pauli antisymmetric wavefunction expressed as the conventional Slater determiment form must be adopted.
So MO theory causes the serious paradoxes where two hydrogen molecule (= H2 ) must always repel each other by unnecessary Pauli repulsion ( this p.3 ), which contradicts the fact that van der Waals attraction is dominant between any molecules at some intermolecular distance, because Pauli antisymmetric wavefunction or Slater determinant always eliminates only molecular attractive exchange energies between electrons with the opposite spins, and only Pauli repulsive exchange energies remain unfairly.
Attraction between the opposite spins (= ↑ ↔ ↓ ) vanishes, and only repulsion between the same spin (= ↑ ↔ ↑, or ↓ ↔ ↓ ) remains in the paradoxical MO.
In order to eliminate this unnecessary Pauli repulsive exchange energies or integral, the MO demands that physicists should use the unrealistic antibond orbitals (= ex. φA - φB ) with unrealistically higher energies.
Because the antibond orbitals can conveniently and fairly eliminate both attractive and repulsive exchange energies in exchange integral between the normal bond (= φA + φB ) and antibond orbitals (= φA - φB ) like
∫ (= φA + φB )( φA - φB ) = ∫φAφA - ∫φBφB = 0
↑ This relation is called "orthogonal" in the integral between the bond and antibond orbitals ( this p.4-3rd-paragraph, this p.1, this 7th-paragraph ).
The problem is the fictitious antibond orbitals always tend to generate energies higher than the actual molecular stable ground state energies.
This MO contradicts the fact that intermolecular attractive energies such as hydrogen bond or van der Waals forces must be always generated between any ordinary stable molecules with the lowest ground state energies.
For example, in all ordinary hydrogen molecules (= H2 ), electrons are almost always in the lowest-energy ground state which must be expressed by the ordinary bond orbitals with lower energies in MO, instead of unreal antibond orbitals with higher energies.
Intermolecular van der Waals attractions should be always generated between the ordinary lowest-energy hydrogen molecules (= bond orbital, Not antibond ), which cannot be explained by the quantum mechanical MO theory which unreasonably eliminates only molecular attractive exchange energies (= integral ) between the opposite spins.
This is one of fatal defects in the ad-hoc molecular orbital (= MO ) theory.
And this is why the original Huckel model representing molecular orbital theory could very roughly deal with only π bonds (= like carbon double bonds, C=C, this p.2-2nd-paragraph ) consisting only of 2p orbitals (= Not considering ordinary σ bond like C-C or H-C based on s orbital ) unreasonably ignoring all interactions except between the nearest neighboring atoms ( this p.8, this p.13-15 ) to hide MO's fatal paradox.
Because unlike s orbitals, each 2p orbital consists of plus and minus phases, so interactions with 2p orbitals can be easily "orthogonal", which can eliminate unnecessary Pauli repulsive exchange energies caused by exchange (= or overlap ) integrals between the same spins ( this last, this p.16, this p.2 ).
So, the molecular orbital (= MO ) theory cannot deal with the ordinary carbo-hydrate molecules consisting mainly of σ bonds (= C-C and C-H ).
Because in these molecules consisting mainly of σ bonds like H-C-C-C-C-H .., unnecessary Pauli repulsive exchange energies cannot be eliminated due to its "non-orthogonality" of s-orbital-based-σ bonds unlike the orthogonal p-orbital-based π bonds, unless the orthogonal destructive σ antibonds with higher energies are paired with the nomal σ bonds.
↑ These higher Pauli repulsive energies or unrealistic antibonds easily make these σ bonds unstable and broken, making the MO contradict the actually-observed molecules. ← MO theory's fatal defects.
Even various later-developed molecular orbital theories such as extented Huckel theory allegedly adding s or σ bonds are all ad-hoc empirical theories based on very rough approximations where all energies of their molecular bond interactions must be artificially adjusted by empirical experimentally-obtained values, Not by useless quantum mechanical theory ( this p.2-4, this p.2-last-paragraph, this p.1-lower, this p.4 ).
The MO theory tries to express the carbon's four valence electrons' orbitals as artificial tetrahedral composite orbitals considering "orthogonal ( this p.5 )"
↑ But even if only carbon's four electron orbitals (= sp3 ) are orthogonal (= eliminating excessive Pauli repulsive exchange energies ), four hydrogen atoms bound to the carbon as a methane (= CH4 ) are Not orthogonal, hence, four hydrogen electrons of CH4 in MO could generate unrealistically higher Pauli repulsive energies than the actual methane ground state energy.
To solve this paradoxes, MO had No choice but to rely on empirical parameters adjusted by experiments (= Not by useless quantum mechanics ) as shown in empirical Huckel bond theory ( this p.2-upper ), and had to replace the original misleadingly-beautiful tetrahedral CH4 structure by ugry complicated composite orbitals ( this p.6, this p.5 ).
↑ And thie failure of the molecular orbital (= MO ) and valence bond theory led physicists to reluctantly choose the more unrealistic one-pseudo-electron DFT as the only remaining approximate method, which also causes serious paradoxes.
(Fig.9) The number of attractive bonds minus repulsive antibonds determines molecular bond formation ?
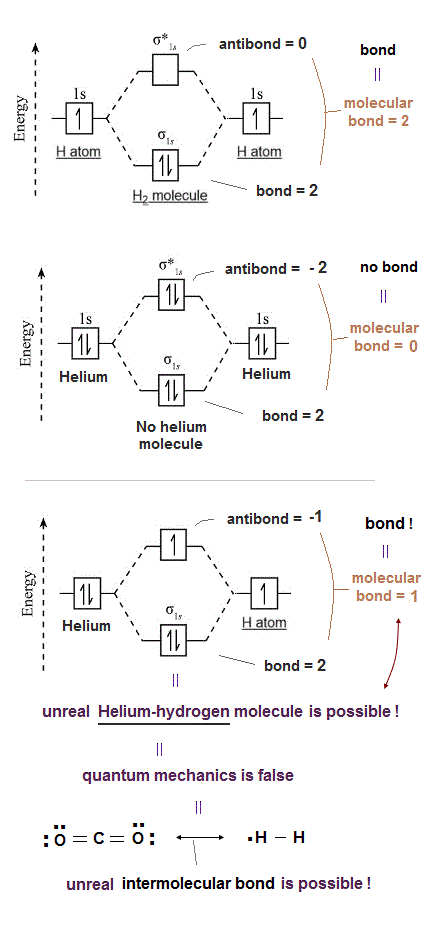
The ad-hoc quantum mechanical leading multi-electron approximate method called molecular orbital (= MO ) theory miserably failed.
According to quantum mechanical molecular orbital theory or Lewis electron structures, the difference between number of attractive bonds and repulsive antibonds is supposed to decide whether molecular attractive bonds are formed or not.
For example, in the simple hydrogen molecule (= H2 ), two electrons with the opposite up and down spins of two H atoms can allegedly enter the same attractive σ bond, and resultantly, form stable H2 molecular attractive bond.
In the case of two helium atoms with 2 × 2 electrons = total 4 electrons, the two electrons with the opposite spins can enter the molecular attractive σ bond orbital, but the other two electrons cannot enter the same σ orbital, instead, two electrons enter the unstable antibond.
As a result, two heliums cannot form molecular attractive bond, because in two heliums, the numbers of attractive bonds (= 2 ) and repulsive antibonds (= 2 ) are the same, then, bonds and antibonds cancel each other, according to the quantum mechanical theory ( this p.3-4 ).
But this molecular orbital theory based on Lewis structure could produce paradoxical non-existent molecular covalent bonds.
When helium (= He with two electrons ) and hydrogen atom (= H with one electron ) try to bond to each other, this causes two attractive bond and one repulsive bond as shown in the above figure, so the total is one attractive bond (= 2 bonds - 1 antibond ) generating unreal He-H molecular covalent bond !
Hence, quantum mechanical molecular orbital theory allowing unreal molecules combining one helium and one hydrogen atom (= He-H ) proves to be wrong.
↑ This quantum mechanical molecular orbital theory based on Lewis structure allows nonexistent molecules, when the total number of valence electrons involved in a pair of atoms is an odd number, like He-H including the hydrogen atom.
For example, a carbon dioxide (= CO2 ) and H2 molecule are independent from each other, and cannot form molecular covanent bond between CO2 and H2 molecules.
But the number of free valence electrons in the oxygen atom of CO2 is one or two, which can form a fictitious molecular attractive covalent bond with one electron of hydrogen atom of H2 molecule.
↑ Two electrons of the oxygen atom of CO2 and one electron of H atom in H2 molecule enter the stable attractive bond orbital (= two ) and antibond (= one ).
Hence, the total is one molecular attractive bond (= 2 - 1 = 1) !
Actually, the true problem of molecualr orbital theory is that two molecules or atoms cannot generate any intermolecular van der Waals attractions. In the upper figure, He-He repulsive antibond energy becomes far larger than He-He attractive bond energy, which disagrees with the fact that two helium atoms weakly attract each other.
The molecular orbital (= MO ) theory suffers fatal flaws where only the molecular attractive exchange energies are unfairly eliminated, and unnecessary Pauli repulsive energies or repulsive exchange integrals remain (= to eliminate this unnecessary Pauli repulsion, MO demands that higher-energy antibonds should be used even in the originally-attractive bond regions, which antibonds also cause contradictory repulsions, too ).
So the MO theory causes the paradoxical situation where two neutral molecules, each of which consists of a pair of spin-up and spin-down (= so two paired spins up and down should cancel each other's repulsion and attraction to be neutral ), must always generate unfairly unnecessary Pauli repulsion contradicting the fact that any two neutral molecules always cause van der Waals or hydrogen bond attractions.
As a result, MO cannot describe any actual intermolecular van der Waals attraction (= non-covalent attractive bonds ).
In fact, quantum mechanical molecular orbitals (= just unphysical mathematical tool ) is unable to explain the clear violation of the octet rule seen in many atoms such as lithium, beryllium, boron, aluminum, phosphorus, sulfur.. and transition metals, and quantum mechanics must rely on various impossible ion formations inside many neutral molecules such as carbon monoxide.
In most solids and crystals, quantum mechanical orbital theory failed, and it must switch into the unphysical band theory described by one-pseudo-electron or fictitious quasiparticles with unreal effective mass and pseudo-charge.
On the other hand, the realistic atomic model based on actually-moving electrons can perfectly explain all these actual molecular bonds without any contradictions which always haunt the quantum mechanics.
Quantum mechanical original Pauli antisymmetric wavefunctions based on spin-up-down (= valence bond or Heitler-London method ) also allow unreal H3 and H4 molecules (= by estimating the total energies by separating Pauli repulsive and molecular attractive bond exchange energies, which is not a legitimate method, because the quantum mechanics cannot describe atoms or molecules with more than two electrons in the common wavefunction with the common normalization coefficient ).
↑ Any types of multi-electron quantum mechanical atomic model ended up in total failure, which forced physicists to choose the more unrealistic and primitive one-pseudo-electron DFT approximation as the only choice for quantum mechanical atomic model, pinning their hope on the impossible dream that as-yet-unknown universal pseudo-potential functional may solve these all molecular paradoxes someday (= never happen ), in vain.
(Fig.10) The most widely-used DFT approximation with one pseudo-electron model fails to explain Pauli exchange or kinetic energies.
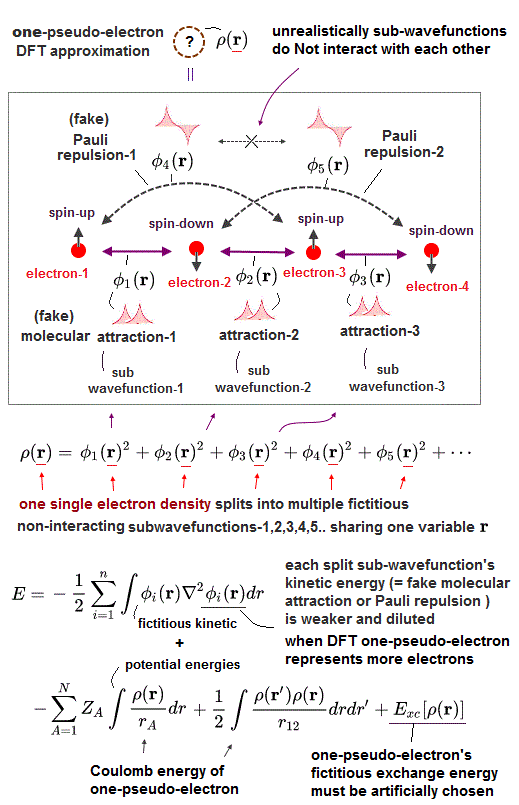
The current most-widely used quantum mechanical approximation is density functional theory (= DFT or Kohn-Sham theory ) which unrealistically contains only one pseudo-electron (= one variable, r ) in freely-chosen fictitious one-electron's effective pseudo-potential energy called exchange correlation functional (= Exc ) which exact universal form is unknown ( this p.3-5 this p.3-left ).
Because there is No such thing as a universally-exact fictitious exchange correlation functional of one-pseudo-electron DFT ( this p.13-23 ).
The current most-widely-used quantum mechanical DFT (= outrageously describing molecules as one-pseudo-electron model with fictitious unknown potential energies ) is a useless fake ab-initio method which can Not predict any physical values ( this p.5-11, this p.2-upper ).
One-pseudo-electron of DFT causes unnecessary Coulomb repulsive energies even inside one-pseudo-electron's negative charge or "self-Coulomb-interaction error problem ( this p.3, this p.7 )" which must be artificially fixed by adding or modifying the unknown exchange-correlation pseudo-potential functional by hand.
It's intrinsically impossible for DFT containing only one pseudo-electron to describe the original quantum mechanical Pauli antisymmetric wavefunctions, because the antisymmetric wavefunctions always become zero when two electrons (= or two electrons' variables r1 or r2 ) are the same one (= r1 = r2 = r ) in DFT.
Antisymmetric wavefunction = ψ(1)φ(2) - φ(1)ψ(2) → when 1 = 2 (= only one electron-1 or only one electron's variable (= r1 or 1 ) exists in DFT ) → ψ(1)φ(1) - φ(1)ψ(1) = 0 ! ← Pauli antisymmetric wavefunctions or Slater determinants (= always zero, when originally-different electrons turn into the same one 1 = 2 = 3 .. ) cannot be used in one-electron model DFT !
Though one-pseudo-electron DFT is currently most widely used as the only hope of quantum mechanical approximation in all physical and chemical academic fields.
Originally, Pauli repulsive energies must be expressed by unphysical antisymmetric wavefunctions causing unphysical exchange energy or destructive interference increasing kinetic energies.
DFT uses only one-pseudo-electron (= only one electron's coordinate or variable r instead of multiple electron's variables r1, r2, r3.. ) to describe its fictitious non-interacting electron's kinetic energy term ( this p.29-31 ), which causes the discrepancy in Pauli repulsive (or molecular fictitious attractive ) exchange kinetic energies between DFT and the original multi-electron Schrödinger equation (= or Hartree-Fock, Slater's antisymmetric determinant using multiple different variables ).
So DFT has to artificially fix this Pauli repulsive kinetic energies by artificially modifying exchange-correlation pseudo-potential energy functionals Exc ( this p.10, this p.20 ), which often fails ( this p.19-21 ).
The exact universal exchange correlation pseudo-potential functional of DFT is Not found as shown in many cases where DFT miserably failed. The choice of different aritificial functionals including different free parameters gives different calculation results ( this p.4 ), showing DFT has No power to predict any physical values ( this p.9 ).
So DFT still has the serious problem of its one-pseudo-electron unable to describe the original quantum mechanical Pauli repulsion expressed by antisymmetric wavefunction originally using multiple electrons' variables (= e1 ↔ e2, e2 ↔ e3, .. )
Like unsolvable multi-electron Schrödinger equations, all DFT equations are unsolvable, hence, physicists have to artificially choose (= guess ) the arbitrary (= unknown, this p.3 ) one-pseudo-electron density function (= or basis set ), integrate them (= instead of solving ), vary freely-adjustable parameters (= coefficients ) to find the lowest energy within artificially-chosen pseudo-wavefunctions ( this p.11 ).
↑ This DFT calculation method is similar to the time-consuming self-consistent variational methods. This process of guessing (= choosing fake wavefunctions or basis sets ) and adjusting coefficient parameters to find the lowest energy within artificially-chosen wavefunctions ( this p.4, this p.7 ) is called "(pseudo-)solving ( this p.20, this p.9 )", but this does Not mean truly-solving DFT ( or Schrödinger ) equation itself, because they just integrate the artificially-chosen pseudo-wavefunctions to get pseudo-total-energies ( this p.7 ) without truly-solving (= truly-solving does Not use the integrals of chosen pseudo-wavefunctions ) them.
And due to the unknown inaccurate exchange-correlation pseudo-potential functionals, DFT often gives the wrong energies contradicting the orginal quantum mechanical variational methods ( this p.40-lower, this p.21, this p.9 ).
One-pseudo-electron DFT causes serious paradoxes when it tries to describe Pauli exclusion principle originally expressed by the multi-electron antisymmetric wavefunctions.
For the one-pseudo-electron DFT to describe Pauli repulsion between two separate atoms, it has to use the destructive interference mechanism of artificially increasing the (pseudo-)electron kinetic energy by the steeper wavefunction.
We can prove DFT is intrinsically unable to explain Pauli repulsion especially when there are more than two electrons in the original multi-electron world.
First, we think about the case where there are three electrons A, B, C, all of which have the same up-spin, hence, Pauli repulsion must be generated between all these three electrons with the same up-spin.
↑ Quantum mechanics does not allow two electrons with the same-directional up-spin to occupy the same orbital or place by causing mysterious strong Pauli repulsion between two electrons with the same spin.
In order to cause the Pauli repulsion or fictitious kinetic energy's increase between two atoms A and C, when the wavefunction around A atom has the positive amplitude (= +φA ), the wavefunction around C atom must have the negative amplitude (= -φC ) so that these two wavefunctions interfere destructively (= φA - φC ) which causes the steeper-slope wavefunction with large curvature increasing the kinetic and total energy as antibond due to shorter de Broglie wavelength ( this p.9-10 ).
In the same way, in order to cause the increase in the fictitious Pauli kinetic energy between two atoms B and C (= all A,B,C wavefunctions are supposed to have the same spin, and of course, all A,B,C atoms must contain only one single same pseudo-electron in DFT ), the wavefunction around B atom must have the positive amplitude (= +φB ) with respect to the negative C amplitude (= -φC ).
↑ But in this case, the fatal paradox arises. The wavefunctions around A and B have the same positive symmetric amplitude (= +φA + φB ) causing constructive interference and molecular bond attraction, though the wavefunctions A and B have the same up-spin (= hence, originally, wavefunctions A and B have to be the opposite phases canceling each other like φA - φB ), which DFT result is against the fact that Pauli repulsive energy must arise between two electrons with the same spin !
As shown in Fig.4, also when the wavefunction φC has down spin, other two wavefunctions φA φB have the same up spin, the paradox arises. ← Quantum mechanics is false.
Two wavefunctions with the opposite spins (= down-spin-φC and up-spin-φA, φB ) must have the same positive symmetric amplitude to cause constructive interference and molecular attractive bond, decrease kinetic and total energy.
↑ It means two wavefunctions φA and φB with the same up-spin also have the same symmetric positive amplitude and cause constructively-interfering molecular bond attraction between them, though two wavefunctions with the same up-spin must cause Pauli repulsive antibond ! This is clearly paradox.
DFT uses only one fictitious electron (= one variable, r ) splitting into multiple fictitious non-interacting-electron sub-wavefunctions using only one common electron variable (= r, this p.22 ) to artificially express the nonphysical kinetic energy functional T ( this p.12, this p.4, this p.19, this p.2 ).
↑ Each artificially-split (= diluted ) sub-wavefunction (= each sub-wavefunction is a part of the total one-pseudo-electron wavefunction, and different subwavefunctions are unrealistically required to be Not interacting with each other, though they share the same one pseudo-electron. ← DFT is contradictory ) allegedly gives (fake) molecular attractive exchange energy or Pauli repulsive exchange energy depending on whether each sub-wavefunction is symmetric or antisymmetric.
It means the most-widely used quantum mechanical DFT methods often failed to express electron's kinetic energy T based on Pauli repulsion originally expressed by multiple different electrons' antisymmetric wavefunctions ( this p.3-1st-paragraph, this p.1-2 ).
The fact that one-electron DFT often fails to describe multiple different electrons' kinetic energies or Pauli principle is called "N or V representable problem" where DFT lacking Pauli repulsion often gives unreal energies far lower than true energies ( this p.3-2nd-last apragraph, this p.5 ).
Recently, physicists try to give up splitting the electron density into multiple fictitious orbits with only one pseudo-electron, and invent more primitive simple version of fictitious kinetic energy called the orbital-free density functional theory in vain ( this p.4-right-lower ).
↑ Clarifying the true detailed atomic bahavior is getting more and more impossible in this one-pseudo-electron DFT !
One-pseudo-electron's entire density ρ(r) in DFT must be artificially split into multiple fictitious independent (= fictitious non-interacting with No physical meaning, this p.14, this p.15 ) sub-wavefunctions like
ρ(r) = [φ1(r)]2 + [φ2(r)]2 + [φ3(r)]2 + [φ4(r)]2 + ..
↑ All these fictitious subwavefunctions contain only one common pseudo-electron's variable r using one common exchange-correlation functional potential, but only when calculating their fictitiously divided kinetic energies, each fictitious subwavefunction is treated like a completely independent non-interacting wavefunction, this is inconsistent and illegitimate.
See this p.21-23, this p.10, this p.29-30, this p.13(or p.24)
↑ The trick of DFT illegitimately avoiding paradoxical wavefunctions is even in the places of originally-
The quantum mechanical decision of whether Pauli repulsion or molecular attraction occurs between atoms based on symmetric or antisymmetric wavefunctions between atoms does Not work due to the fatal paradoxes, when there are more than two electrons, especially in the case of one-pseudo-electron DFT which can use only one position variable r.
One-pseudo-electron DFT can show only one fixed set of the wavefunctions, which always becomes paradoxical or canceled out to be zero due to the fact that the antisymmetric wavefunctions including only one electron or variable are always zero (= or even multi-electron antisymmetric wavefunctions mixing molecular attractive and Pauli repulsive exchange energies always become zero. ← quantum mechanical wavefunction with its unphysical Pauli principle itself is wrong ).
↑ Pauli antisymmetric wavefunction ψ(r1, r2 ) = - ψ(r2, r1) → when the wavefunction ( like of DFT ) contains only one variable r1 = r2 = r, → ψ(r, r ) = - ψ(r, r) → 2ψ(r, r) = 0. ← Antisymmetric wavefunction with only one variable becomes zero.
↑ So in order to avoid this paradoxical situation, DFT unscientifically tries to generate fictitiously-divided sub-wavefunctions in the original zero-amplitude places like 0 = +φ1(r) - φ2(r), and calculate the fictitious kinetic energy of each sub-wavefunction +φ1(r) and -φ2(r) independently (= on the pretext of "non-interacting" ), then, square those sub-wavefunctions (= for preventing those sub-wavefunction amplitudes from being canceled or returned to zero ), sum them up to produce the whole one-pseudo-electron density ρ(r) = [φ1(r)]2 + [φ2(r)]2 + [φ3(r)]2 + .. which trick is illegitimate and inconsistent.
The serious problem arises as shown in Fig.8.
If DFT tries to explain actual electron's kinetic energies by these fictitiously-divided independent smaller sub-wavefunctions (= φi(r) ) or orbitals, DFT has to divide the entire electron's density (= ρ(r)) into many more smaller pieces or smaller fictitious probability sub-wavefunctions (= each contains smaller electron's charge density ) to explain more interatomic Pauli repulsive or molecular attractive interactions (= depending on whether each sub-wavefunction takes symmetric or antisymmetric form )among all electrons, as the number of electrons increases.
↑ The more electrons are contained in the system, the more different Pauli repulsion or molecualr attractive interactions among all possible pairs of electrons have to be considered. → DFT has to divide the original entire electron's density (= ρ(r)) into more smaller pieces or smaller independent probability sub-wavefunctions which can generate only far smaller interacting energy based on smaller divided electron's density than the actual interatomic energies.
As shown in Fig.8, when there are only two electrons, the number of the interatomic interaction or bond is only one (= between two electrons ), so the entire two electrons' charge density can concentrate on this single interatomic interaction.
But when there are six electrons, the number of the interatomic interactions such as Pauli repulsion and molecular attraction increases to fifteen (= interactions between neighboring atoms, interactions between atoms which are two or three atoms apart ), hence, the entire six electrons' charge density must be divided into smaller pieces in each interaction (= 6 electrons must be divided into 15 interactions, each of which contains only 6/15 smaller split electron, compared to 2 electrons contained in one single bond when there are two electrons ! )
↑ So this fictitiously-divided independent sub-wavefunctions of one-pseudo-electron DFT cause new fatal paradoxes where interatomic interactions become weaker and diluted, as we consider more electrons (= needing more fictitiously-divided independent sub-wavefunctions as the increasing number of interatomic interactions of more electrons ) in the system, though in the actual world, each interatomic energy or strength remains the same irrespective of how many electrons we consider in the whole system.
And these DFT fictitious sub-wavefunctions can Not avoid unreal H3 or H4 molecules, which is another proof that quantum mechanics and its DFT are wrong theories.
(Fig.11) Hydrogen molecule ion (= H2+ ) Schrödinger equation is unsolvable
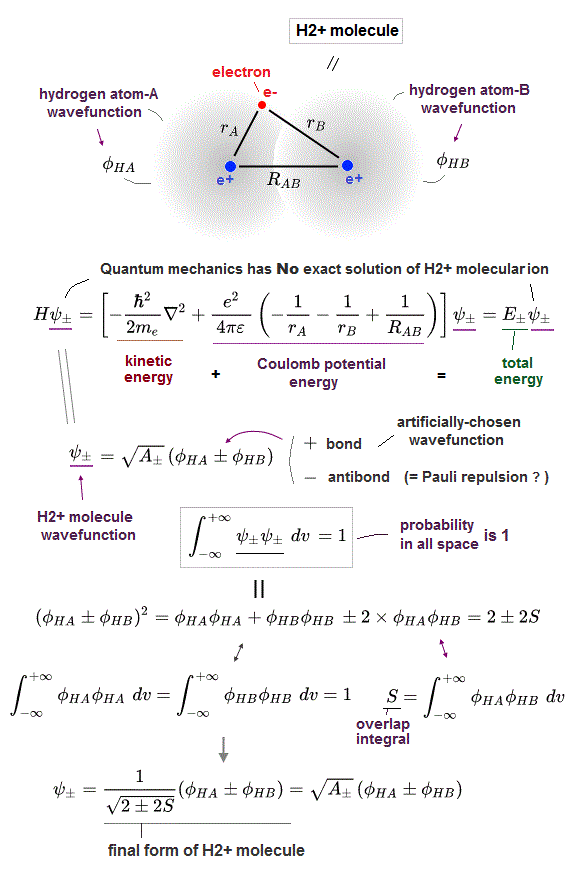
Contrary to the media-hype, quantum mechanics is unable to obtain the exact analytical solution also in hydrogen molecule ion (= H2+ ) with only one electron and two nuclei ( this p.8-9 ).
Physicists had to artificially choose approximate models or fake wavefunctions = basis sets ( this p.2, p.19-upper ), quasi-atomic wavefunction ( this p.1-left-last-paragraph, p.2-left-last-paragraph ) to seemingly guess the numerical solution of H2+
For example, in this paper ( this p.4-right ), physicists have to rely on some artificial numerical algorithm and the deliberately-chosen (fake) approximate polynomial wavefunctions consisting only of four fictitious terms instead of analytically solving Schrodinger equation for H2+ molecule ion.
We proved that quantum mechanical Schrödinger equation for H2+ molecular ion can never have the exact solvable solutions due to its unrealistically-spreading probability wavefunction.
↑ Schrödinger equation uses exactly the same mechanism of total energy equal to the sum of Coulomb electric potential energy and electron's kinetic energy expressed as de Broglie wavelength as the successful Bohr's realistic model.
So if Schrödinger equation really could obtain analytical solution of H2+ molecule ion, Bohr's model also could get the analytical solution like hydrogen atom.
↑ Because if Schrödinger equation for hydrogen molecule ion (= H2+ ) could really obtain exact solution or wavefunction, it means the Schrödinger's electron can also move smoothly along the exact continuous and smooth wavefunction obeying the constant total energy where the sum of Coulomb potential energies and the electron's kinetic energy (= expressed as the same de Broglie wavelength as Bohr's model ) must be always conserved and constant.
And if there was the exact wavefunction and solution, all points on the wavefunction need to connect with each other continuously and smoothly (= if the wavefunction suddenly discontinues, electron's kinetic energy expressed as the derivative or slope of the wavefunction becomes infinite violating total energy conservation ), which means the exact Schrödinger's wavefunctions must obey the rule of an integer multiple of de Broglie wavelength in one closed smoothly-connected continuous orbit like Bohr's model.
↑ As a result, if Schrödinger equation for H2+ molecule ion could really obtain analytical exact wavefunction (= obeying Coulomb potential + de Broglie wavelength + conserved constant total energy E ), we can pick one orbit out of the Schrödinger's H2's as-yet-unseen exact analytical wavefunction as Bohr's orbit, hence, Bohr's atoms also proved to be right for H2+ molecule ion.
Furthermore, if Schrödinger equation really could obtain analytical solution of H2+ molecule ion, only H2+ molecule ion deos Not rely on unphysical exchange energy, unlike other quantum mechanical molecular bonds, because the exchange energy can Not be obtained under the condition of total energy conservation law (= this is why unphysical exchange can be obtained only by "integral" instead of analytically solving Schrödinger equations )
Analytical solution conserving total energy E should have contained only Coulomb potential energy as molecular bond energy, Not relying on exchange pseudo-energy, hence the as-yet-unseen analytical H2+ solution disagrees with the current mainstream quantum mechanical molecules heavily relying on fictitious exchange energies instead of Coulomb energies ( this p.11 ).
Basically, in actual atoms and molecules which are always thermally fluctuating randomly, Coulomb force alone cannot always keep the closed smoothly-connected orbits (= closed orbits correspond to the analytical Schrödinger solution or wavefunction connecting all dots smoothly and continuously ). ← The stable smoothly-connected closed orbit needs to be always kept and stabilized by some realistic external force or factor such as de Broglie wave interference even in the rapidly-fluctuating atomic states.
↑ We need to know the precise electron's de Broglie wave interference power or pressure, which always keeps the wave amplitudes in phase with each other for avoiding destructive interference (= like wave crest of lower density area and the trough of higher density area naturally attract and connect with each other as shown in the observed longitudinal wave ).
But quantum mechanical unphysical exchange energy concepts lacking real forces prevent us from proceeding and designing new practical atomic experiments using realistic atomic model, instead, the quantum mechanical unphysical model forces us to use unreal quasiparticles and one-pseudo-electron DFT. → Our science stops progressing.
Here we directly calculate the total energy, electron's kinetic energy and Coulomb potential energy of quantum mechanical hydrogen molecule ion (= H+ ) in both molecular attraction (= symmetric wavefunction ) and Pauli repulsion (= antisymmetric wavefunction ), and confirm quantum mechanics cannot conserve the constant total energy E (= the sum of electron's kinetic energy and potential energies is Not conserved inside a quantum mechanical molecule ), and quantum mechanical theory is proved to be wrong.
Hydrogen molecule ion (= H2+ ) consists of two positive nuclei (= proton e+ ) and one negative electron (= e- ), which can form the weak attractive molecular bond.
↑ From the commonsense point of view, this one negative electron between two positive nuclei works as a binder of them through Coulomb attractive force.
But as I said, quantum mechanical probability wavefunction or electron cloud spreading all over the place can Not generate Coulomb attractive energy enough to form covalent bonds including H2+ molecule ion.
So quantum mechanics has to rely on nonphysical exchange energies expressed as exchange integral by forcing a single electron to exist in multiple different separate nuclei simultaneously ( this p.11 ) and violating the inviolable total energy consevation law.
The (constant) total energy E is the sum of the electron's kinetic energy expressed as the derivative of the wavefunction and the three Coulomb potential energy terms.
Three Coulomb potential energy terms of H2+ consists of two attractive electric energies based on the distance between the electron and the nucleus-A (= rA ) and the distance between the electron and the nucleus-B (= rB ) and one repulsive energy based on the distance between two nuclei (= RAB ).
Quantum mechanics often chooses the approximate (= fake ) trial wavefunction = linear combination of two hydrogen atomic wavefunctions φHA and φHB whose nuclei are serapated by the distance RAB.
φHA and φHB are the normalized hydrogen atomic 1s wavefunctions around the different separate center nuclei ( first, we think about the simplest case of the effective nuclear charge Z exponent of hydrogen wavefunction being 1 = Z ).
ψ+ = φHA + φHB is the constructively-interfering wavefunction forming attractive molecular bond by allegedly decreasing kinetic and total energies. ← This decrease in kinetic energy in H2+ molecular bond exchange energy will be calculated and confirmed later.
ψ- = φHA - φHB is the destructively-interfering wavefunction blocking H2+ molecular bond formation by causing Pauli repulsion increasing the kinetic energy by increasing the wavefunction curvature ( this p.9-10 ), which will be also actually calculated and confirmed later.
Quantum mechanical Schrödinger equations for all multi-electron atoms and molecules are unsolvable, so physicists have to integrate the chosen (fake) trial wavefunctions with the Schrödinger's Hamiltonian energy operator (= H ).
The probability of electron is expressed as the product of two wavefunction (= amplitude ) like the probability = ∫ ψψ = 1 ← The total probability obtained by integration in all space must be "1" = called "normalization".
Based on this condition of the total probability density equal to 1, we can determine the coefficients of H2+ wavefunctions like the upper figure ( this p.3 ) where S is the overlap integral of two different hydrogen atomic wavefunctions ∫ φHA φHB ( this p.6-7 ).
(Fig.12) Calculation of the expected total energy E± of H2+

By putting Schrödinger energy equation (= Hamiltonian H = the sum of kinetic and potential energy ) between two chosen H2+ wavefunctions and integrating it in all space, quantum mechanics tries to obtain the expectation (= average ) total energy E without solving (unsolvable) Schrödinger equations ( this p.6 ).
HAA = ∫ φHA(r)H φHA(r) dr is the normal Coulomb integral
HAB = ∫ φHA(r) H φHB(r) dr is the unphysical exchange integral ( this p.9-11 ).
EH1s = the ordinary hyrogen atomic ground state total energy (= -13.606 eV, this p.5, this p.17, n = 1, Z = 1 ) expressed as the sum of kinetic energy acting on one hydrogen atomic wavefunction and one Coulomb potential energy with the same nuclear center as the hydrogen atomic wavefunction like in solving the ordinary one-electron hydrogen atomic Schrödinger equation.
(Fig.13) ↓ Integral formulas in H2+ molecule ion ( Z = 1 ).
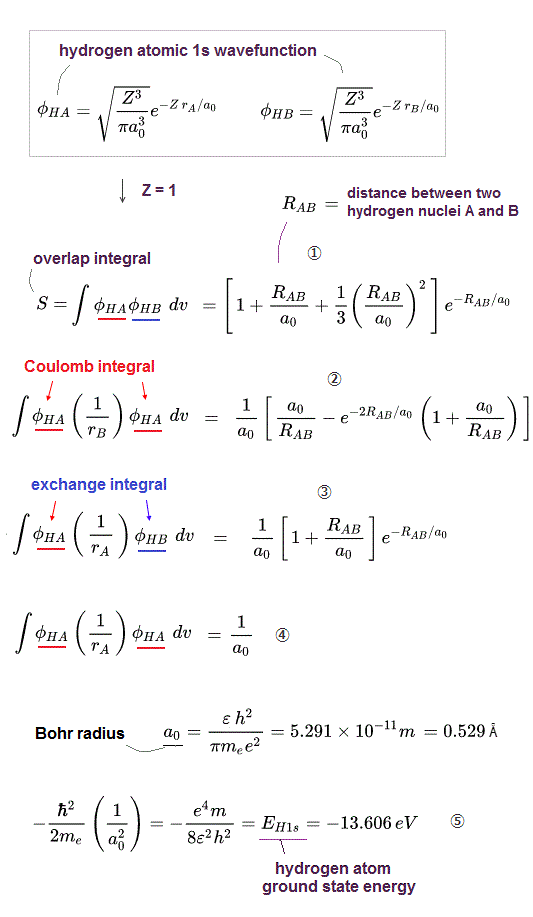
Fig.13 shows several formulas of the integral used in calculating the expectation total energy E of H2 molecule ions ( this p.4, this, this p.2-3 ).
The constant a0 is Bohr radius = 5.291 × 10-11 meter = 0.5291 Å
RAB is the distance (= meter or Å ) between two nuclei of hydrogen atoms φHA and φHB.
EH1s is the ordinary hydrogen atomic 1s ground-state ( n = 1, Z = 1 ) total energy E = -13.606 eV ( this 11.10.5, this p.5, this p.4, this p.4 ).
The upper formula of Fig.13 is in the case of the effective nuclear charge exponent Z = 1.
If we want to use trial hydrogen-like atomic wavefunctions which are contracted by the exponent parameter Z bigger than 1, we just replace the Bohr radius (= a0 ) of Fig.13 by a0/Z as seen in this.
(Fig.14) H atomic 1s wavefunction φHA and φHB with Z > 1

Fig.14 is the case of using H atomic wavefuntion with exponent parameter Z bigger than 1.
This parameter Z exponent of hydrogen-like 1s atomic wavefunction must be determined by variational method finding the lowest total energy E within the chosen trial wavefunctions, after integrating the chosen wavefunctions.
When the kinetic energy term expressed as the derivative operator (= ∇2 ) acting on the H-atomic 1s wavefunction with Z exponenet parameter, this kinetic energy becomes Z2 × the original kinetic energy of the simple H-atom of Z = 1.
↑ In order to cancel the change of this kinetic energy and get the constant total energy E, we need to divide one Coulomb potential energy term like -e2/4πϵ r = -Z e2/4πϵ r + (Z-1)e2/4πϵ r.
↑ This artificial -Z e2/4πϵ r potential energy term can cancel kinetic energy term and give the constant total energy of hydrogen atoms with Z > 1 = Z2 × the original H-atom ground state energy (= Z2 × EH1s = Z2 × -13.606 eV, this p.2,5 ).
The remaining additional artificially-generated Coulomb energy term of (Z-1)e2/4πϵ r can be calculated using the formula of Fig.13 ③ and ④.
So when we consider the case of the exponent parameter Z bigger than 1, the final form of H2+ molecular ion's total energy changes from Fig.12 to Fig.14 (= when inserting Z = 1 into Fig.14 equation, you can get Fig.12 equation ).
(Fig.15) Computing kinetic and total energyes at (x,0,0) in H2+
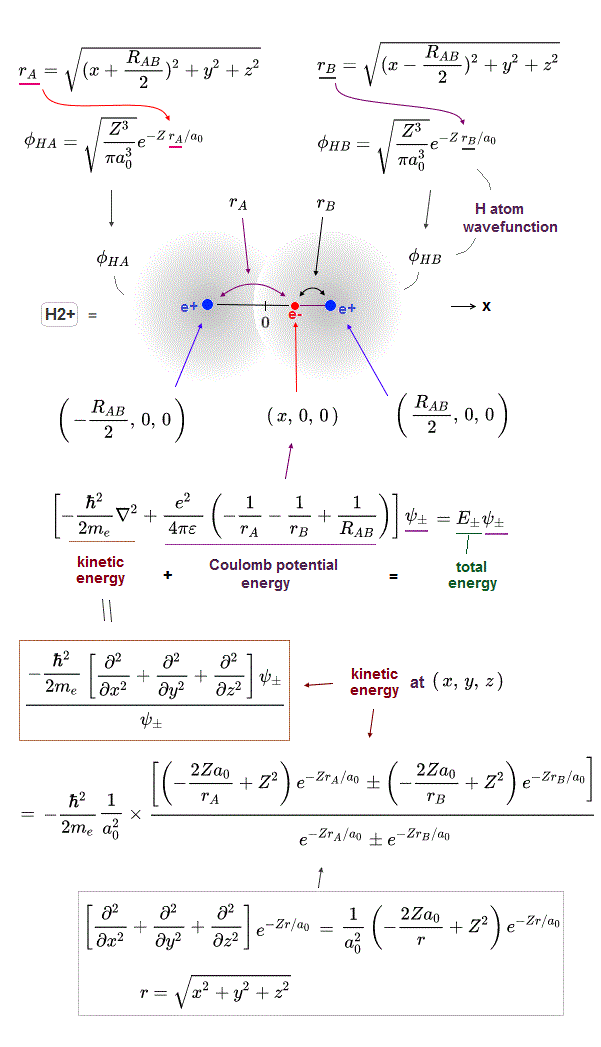
Instead of getting the average total energy values in all places, we want to know the electron's kinetic energy (= derivative acting on wavefunction ) and potential energy in each different single position = ( x, 0, 0 ) on the x-axis.
Two HA and HB atomic nuclei separated by the distance of RAB exist at ( -RAB/2, 0, 0 ) and ( +RAB/2, 0, 0 ) respectively.
The electron's kinetic energy value at each place can be obtained by dividing the derivative acting on H2+ wavefunctions (= ψ± = φHA ± φHB, this 14.2 ) by the original wavefunctions themselves like kinetic energy = [(-ℏ2/2m ∇2 ) ψ±]/ψ±. ← constant coefficient of wavefunction is canceled to be 1 by numerator divided by denominator
And we can also calculate Coulomb potential energy at each different positions of (x,0,0) summing three Coulomb energy terms ( this p.4 ) in H2+ molecule ion.
If we insert some x-coordinate value into the above kinetic and Coulomb potential energy terms, we can know kinetic, Coulomb and total energies at the electron's different position of (x,0,0) separately.
And we can prove quantum mechanical H2+ molecule ion generates fake molecular attraction and Pauli repulsion by decreasing and increasing pseudo-kinetic energies which obviously violates total energy conservation law (= total energies E = sum of kinetic and potential energies are changed and different in the electron's different positions of x inside a single H2+ molecule ion ).
It proves quantum mechanics is wrong.
(Fig.16) JAVA program to compute H2+ energies.

Here, we actually compute the electron's kinetic energies, total energies both in H2+ molecule ion bond (= attractive molecular bond ) and antibond (= Pauli repulsion ).
Sample JAVA program to compute H2+
You can copy and paste the above simple JAVA program into a text editor, you can easily complile and run this.
(This class file name is hyios, so save this text editor as "hyios.java", and compile it.)
After running this program, we are asked to input the distance between two H atoms (= angstrom ) and exponent parameter Z.
For example, we input " 1.32 " as the distance (= RAB = 1.32 angstrom, 1.32 Å or 1.32 × 10-10 meter ) between two H atom in H2+ molecule ion, and input " 1 " as the exponential parameter Z of hydrogen-like 1s atomic wavefunction
This program outputs H2+ bond (attractive) energy = -1.764139 eV and H2+ antibond (Pauli repulsive ) energy = +5.726666 eV
↑ This means the total energy of H2+ molecular attractive bond based on the symmetric wavefunction is 1.764139 eV lower at the internuclear distance RAB = 1.32 Å (= this is the lowest and most stable energy, when Z = 1 ) than the original dissociated H-atom and H+ proton separated by the infinite distance.
↑ This quantum mechanical simplest way's calcualted value of H2+bond energy = -1.76 eV at the interatomic distance RAB = 1.32 angstrom agrees with other sites ( this p.18, this last, this last, this p.5 ), which disagree with the experimental value of H2+ bond energy is -2.79 eV at the interatomic distance RAB = 1.057 angstrom.
And the total energy of H2+ Pauli repulsive antibond based on antisymmetric wavefunction is higher than the original separate H-atom and H+ proton by 5.726666 eV.
↑ H2+ Pauli antisymmetric wavefunction clearly gives total energy higher than the original energy.
Next input x-coordinate of the electron's position as "0.2 (= angstrom )".
This program outputs the original kinetic energy = 17.698283 eV at the position of x = 0.2 in the original separate single HB hydrogen atom.
↑ Here, the original isolated H atom is supposed to mean HB atom. so the distance between the electron at x = 0.2 Å and the original isolated H atomic (= HB ) nucleus is 1.32/2-0.2 = 4.6 Å. ← The electron's kinetic energy at the position of 4.6 Å apart from the nucleus in the original isolated H atom is 17.698283 eV.
This kinetic energy becomes lower to 13.045750 eV in the H2+ symmetric wavefunction, and become higher to 30.588979 eV in the H2+ Pauli antisymmetric wavefunction.
↑ This result clearly shows quantum mechanical molecular attractive exchange energy originates from the lowered kinetic energy and Pauli repulsive exchange energy originates from the higher kinetic energy (= with No real force or potential energy causing these kinetic exchange energy change ! ) instead of Coulomb electric force.
The original Coulomb energy = -31.304283 eV means Coulomb potential energy between an electron and a single hydrogen atomic (= HB ) nucleus in the original isolated H atom at x = 0.2 Å (= which means 4.6 Å apart from the original isolated H or HB atomic nucleus ).
↑ So the sum of the original kinetic (= 17.698283 eV ) and Coulomb potentiel energy (= -31.304283 ) becomes the original isolated hydrogen atomic wavefunction's total energy of -13.606 eV (= 17.698283 - 31.304283 )
And the total Coulomb potential energy (= -37.139366 eV ) is the sum of all three Coulomb potential energy terms (= Coulomb attraction between the electron and two H atomic nuclei + repulsion between two H nuclei ) at the position of x = 0.2 Å
Total energy-symme (eV) means the symmetric wavefunction gives the total energy -10.487515 eV (= total energy change from the dissociated H atom and H+ at 0.2 Å position ) and the antisymmetric Pauli wavefunction gives the total energy = +7.055614 eV.
↑ In the symmetric H2+ wavefunction, even when the electron is closer to the other (=HA) nucleus and lowers Coulomb potential energy, the electron's kinetic energy becomes lower. ← Though in order to conserve total energy, kinetic energy needs to be higher when potential energy is lower !
And H2+ antisymmetric wavefunction's total energy at 0.2 Å position is +7.055614 eV higher than when H atom and H+ are separated by infinite distance. ← This Pauli repulsive higher energy clearly originates from the increased kinetic energy by the steeper destructive interfering antisymmetric wavefunction.
(Fig.17) Kinetic, total energies at the position x = 1.12 Å of H2+ molecule ion where two H atomic nuclei are separated by 1.32 Å

Next, after running this program, we input the same RAB = "1.32 (Å)" as the interatomic distance, the exponent parameter Z = 1, and input the electron's position x = 1.12 (Å).
Also at this position of x = 1.12 Å, the electron's kinetic energy becomes lower to 15.928207 eV from the same position of the original independent H-atom (= 17.698283 eV ), in this H2+ symmetric wavefunction.
And the kinetic energy at the same position of x = 1.12 Å of H2+ antisymmetric wavefunction becomes higher to 19.786862 eV from the original 17.698383 eV of the isolated H atom.
Total energy of this H2+ symmetric wavefunction at the position of x = 1.12 Å is +1.049122 eV higher than the original isolated H atom (= due to being more distant from the other HA nucleus ), which is far higher than -10.487615 at the position of x = 0.2 (= closer to the other positive nucleus ).
↑ This means total energies at different positions (= x = 0.2 Å and 1.12 Å ) give completely different total energies, which shows total energy is Not constant or conserved in the electron's different positions inside a single H2+ quantum mechanical molecule.
Violation of the inviolable total energy conservation law means quantum mechanical molecule is false.
(Fig.18) Total energies at different positions x = 0.2 Å and x = 1.12 Å are different and Not conserved in a single quantum mechanical H2+ molecule ion !
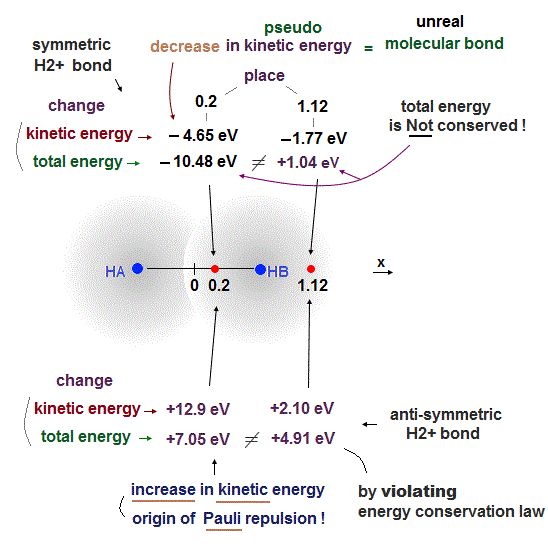
By comparing the calculation results of total energy at the position of x = 0.2 Å (= -10.48 eV ) and the total energy at x = 1.12 Å (= +1.04 eV ), these results clearly show the total energy is Not constant or conserved inside a quantum mechanical H2+ molecule ion.
Total energy E must be always conserved and constant also inside quantum mechanical atoms and molecules.
This result proves quantum mechanics is false.
In both positions of H2+ symmetric wavefunction (= constructively interfering wavefuntion with gentler slope ), the electron's kinetic energies become lower than that of the original isolated H atom, which confirms the fact that quantum mechanical molecular bond is driven by the decrease in the kinetic energy resulting from unphysical exchange energies lacking real forces.
Also in H2+ antisymmetric wavefunction causing antibond, the total energies are different, Not conserved at different positions of x = 0.2 Å (= +7.05 eV ) and x = 1.12 Å (= + 4.91 eV ).
↑ The position of x = 0.2 Å is closer to the other positive HA atomic nucleus, but due to the destructive interference causing steeper wavefunction between two H atomic wavefunctions, it drastically increases kinetic energies ( kinetic energy increase = +12.9 eV (= +30.6 - 17.7 eV ) at x = 0.2 Å compared to +2.10 eV (= +19.8 - 17.7 eV ) at x = 1.12 Å ), and resultantly increases the total energy in H2+ Pauli repulsive antisymmetric antibond.
(Fig.19) H2+ molecule ion, internuclear distance RAB = 1.06 Å and exponent parameter Z = 1.24 (= contracted H atoms ).

After running this program,we input RAB "1.06 (Å)" as the internuclear distance, the exponent Z parameter = 1.24 (= using contracted H atoms ), and the position x = 0.2 Å
In this case ( Z = 1.24, RAB = 1.06 Å ), H2+ molecular bond attractive energy becomes -2.354069 eV (= this is the lowest and most stable H2+ bond energy, when using one freely-changeable Z exponent variational parameter ), agreeing with other sites ( this p.21, this p.8 this p.14 ).
The experimental energy of H2+ molecule ion is 2.79 eV at the internuclear distance RAB = 1.057 Å
Also in this case ( Z > 1 ), the electron's kinetic energy decreases to 24.843892 eV from the original isolated H atom (= 30.030273 eV ).
↑ Coulomb potential energy becomes lower at this position of x = 0.2 Å due to being closer to the other positive nucleus, but the electron's kinetic energy becomes lower, too (= total energy is Not conserved. If total energy is conserved, electron's kinetic energy becomes higher to cancel the lowered Coulomb potential energy ).
This result shows also in H2+ molecule ion using the contracted H atoms with exponent parameter Z > 1, the kinetic energy decrease is the source of quantum mechanical unphysical exchange molecular bonds ( this p.6 ).
(Fig.20) H2 molecule. RAB = distance between two nuclei of hydrogen atoms φHA and φHB.
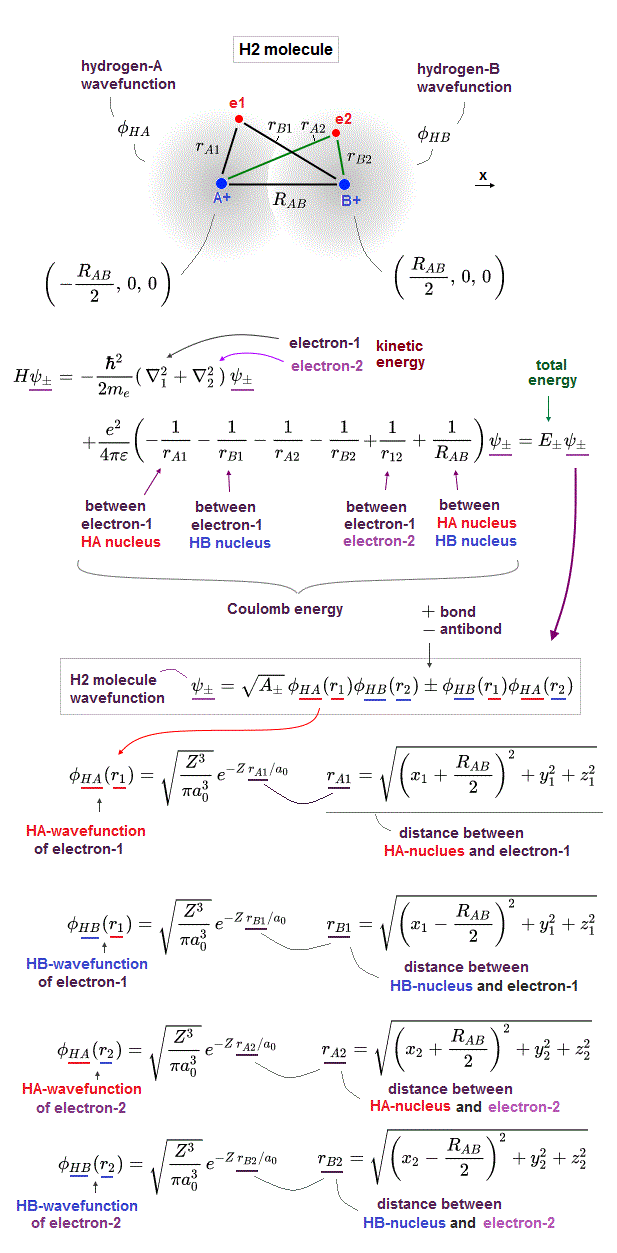
Here we calculate energies of hydrogen molecule (= H2 ) consisting of two hydrogen atomic 1s wavefunctions (= φHA and φHB ) with two electrons (= e1 and e2 ).
Hydrogen molecular total energy or Hamiltonian (= H ) consists of kinetic (= ∇1 = electron-1, ∇2 = electron-2 ) energies expressed as derivatives and six Coulomb energy terms; attractions between two electrons and two nuclei, repulsions (= interelectronic and internuclear ).
In order to generate quantum mechanical unphysical exchange energies ( + = molecular attractive bond, - = Pauli repulsive antibond ), two electrons need to unscientifically exist in two hydrogen atomic wavefunctions simultaneously using parallel worlds.
↑ It needs two different wavefunctions in each electron where φHA(r1) is the hydrogen atom-A wavefunction containing electron-1 and φHB(r1) is the hydrogen atom-B containing electron-1
Quantum mechanical unphysical Pauli principle rule requires all wavefunctions to take the form of antisymmetric wavefunctions where exchanging any two electrons should flip the sign of the entire wavefunction.
↑ Precisely, Pauli antisymmetric wavefunctions have fatal flaws = cannot generate molecular attractive bond energies between two electrons with the opposite spins, so this molecular bond exchange energy is irrelevant to Pauli repulsive antisymmetric wavefunction.
When two electrons have the opposite spins (= antiparallel, antisymmetric spins or singlet ), the spacial H2 molecular wavefunction becomes symmetric (= so the entire wavefunction consisting of spacial and spin parts becomes antisymmetric, after all ).
This (spatial) symmetric H2 wavefunction with the opposite spins is supposed to form attractive molecular bond by unphysical exchange energies or the constructive interference decreasing (pseudo-)kinetic energies (= No physical reality, this p.8-last-paragraph ).
When two electrons have the same spins (= parallel, symmetric spins or triplet ), the spacial H2 molecular wavefunction must take the antisymmetric form.
This (spacial) antisymmetric H2 wavefunction with the same spin is supposed to generate Pauli repulsive exchange energies (= antibond ) and block H2 molecular covalent bonds by increasing total enegies based on increasing (pseudo-)kinetic energies (= with No real force, either, this p.9-10 ).
(Fig.21) Probability = ∫ψψ = 1 determines coefficient.
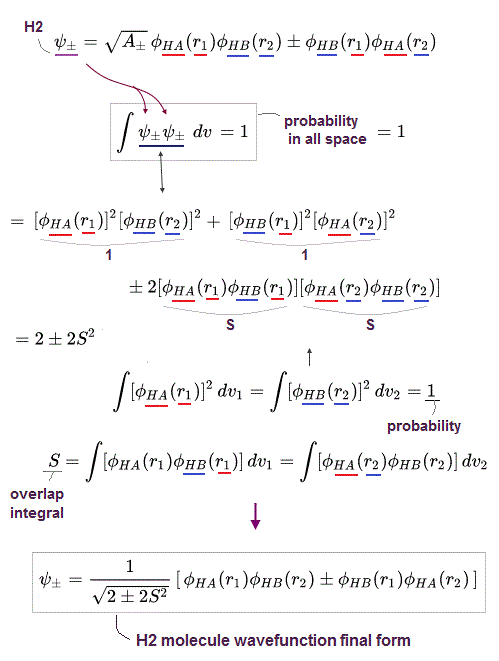
The probability expressed as the integral of the product of two same wavefunction ( probability = ∫ψψ ) must be always "1" or you can use this form.
This condition of all probability = 1 called normalization can determine the coefficient of H2 molecular wavefunction where S = ∫ φHA(r1)φHB(r1) = ∫ φHB(r1)φHA(r1) is called the overlap integral ( this p.20 ).
(Fig.22) Total energy E = ∫ ψ H ψ H = Hamiltonian
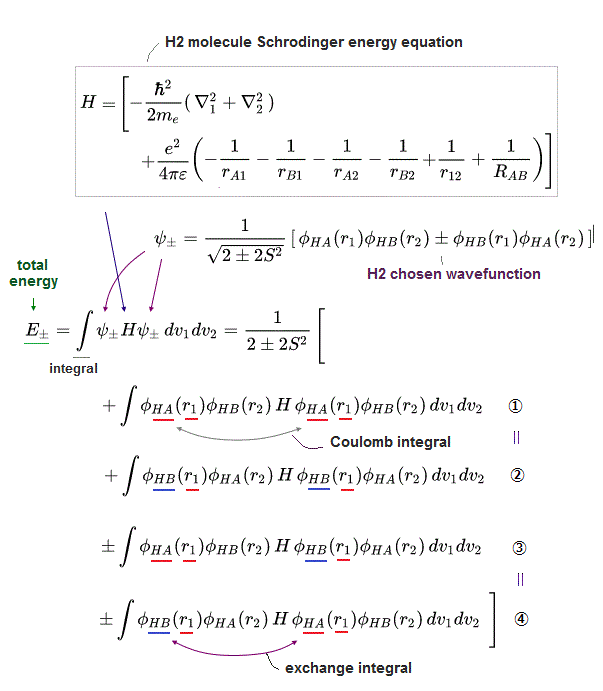
H2 molecular average (fake) total energy can be obtained by integrating the chosen H2 wavefunction (= ψ+ = symmetric, ψ- = antisymmetric ) with H2 Schrödinger energy equation or Hamiltonian instead of solving the unsolvable H2 molecule Schrödinger equation.
This resultant energy equation contains Coulomb energy integral and unphysical exchange energy integral ( this p.14 ).
↑ The sign of this unphysical exchange energy integral originating from the symmetric or antisymmetric H2 wavefunctions determines whether molecular attractive bond or Pauli repulsive antibond is generated ( this p.3-4 ).
(Fig.23) Z2 EH1s = Z2 × H atom ground state energy
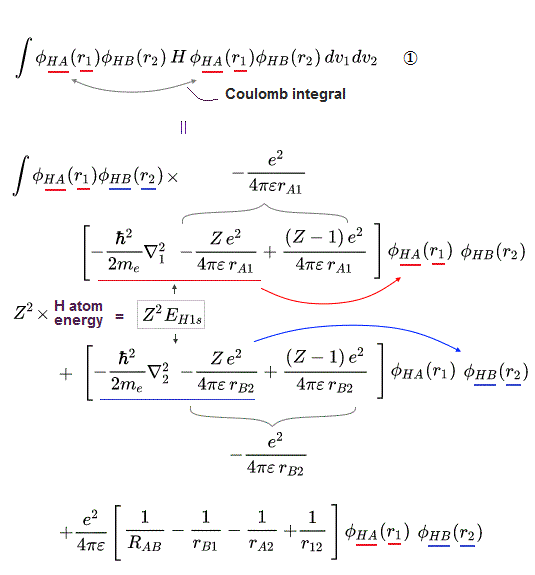
When computing Coulomb energy integral term of H2 molecule, we use the generalized hyrogen atomic 1s wavefunction with arbitrary exponent parameter (= Z = 1 or Z > 1 ) like H2 molecule ion.
In order to incorporate this Z exponent other than 1, We need to divide one hydrogen Coulomb energy term like -e2/4πε rA1 → -Ze2/4πε rA1 +(Z-1)e2/4πε rA1.
The sum of kinetic energy term expressed as the derivative and one of divided Coulomb energy term (= -Ze2/4πε rA1 ) acting on one HA-atomic 1s wavefunction can give the simple constant total energy E (= regardless of electron's position ) of Z2 EH1s = Z2 × H atom ground state ( n = 1 ) energy (= Z2 × 13.606 eV, this p.4, this p.5 ).
The other remaining artificially-generated Coulomb energy term (= +(Z-1)e2/4πε rA1 ) must be calculated using the formula of Fig.13 (= Fig.13 integral formula is obtained in the case of Z = 1, so you need to replace Bohr radius = a0 of Fig.13 formula by a0 divided by Z or a0/Z when we use the contracted H 1s atomic wavefunction with Z exponent ).
The same artificial division of the original Coulomb energy term must be done also in φHB wavefunction.
(Fig.24) Kinetic energy derivative ∇1 acts only on electron-1 wavefunction.

Kinetic energy term is expressed as derivative, and the derivative-1 (= ∇1 ) acts only on H atomic wavefunctions containing electron-1, and derivative-2 (= ∇2 ) acts only on H atomic wavefunctions containing electron-2.
And r12 means the distance between electron-1 at (x1,y1,z1) and electron-2 at (x2,y2,z2). this p.5
(Fig.25) Coulomb energy integral in H2 molecule.
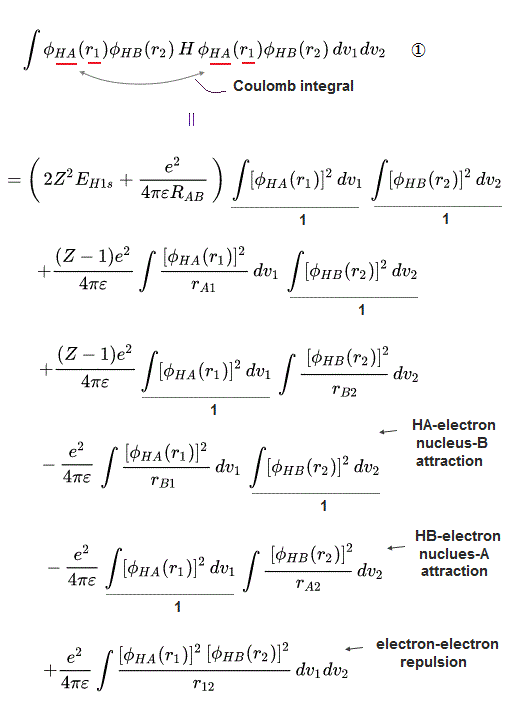
From Fig.23 and the fact that the total probability of the product of the same two H-atom wavafunction becomes 1 ( ∫ φHA(r1) φHA(r1) = ∫ φHB(r1) φHB(r1) = ∫ φHA(r2) φHA(r2) = ∫ φHB(r2) φHB(r2) = 1 ), we can get the final form of Coulomb integral of H2+ molecule.
(Fig.26) Z2 × EH1s = H atom ground state constant energy.
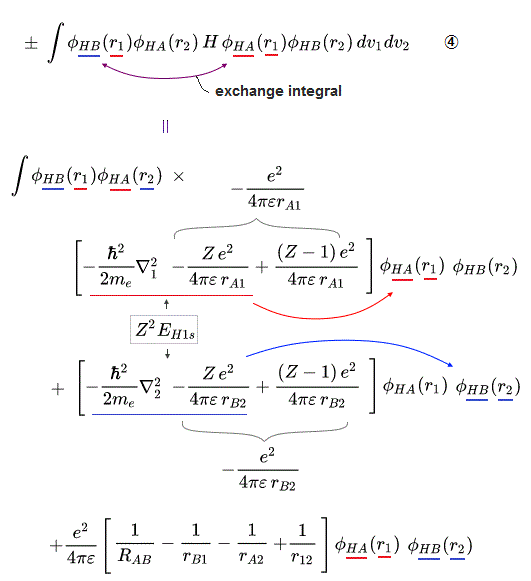
We can compute exchange integral of H2 molecule consisting of hydrogen atomic 1s wavefunctions with Z exponent (= effective nuclear charge Z ), in the same way as Coulomb integral.
Z2 × EH1s = Z2 × 13.606 eV (= H atom ground state energy, n = 1 ).
(Fig.27) Exchange integral in H2 molecule with Z exponent parameter

From Fig.26, we can obtain the final form of exchange integral of H2 molecule.
S = ∫ φHA(r1) φHB(r1) dv1 = ∫ φHB(r1) φHA(r1) dv1 =∫ φHA(r2) φHB(r2) dv2 = ∫ φHB(r2) φHA(r2) dv2 =exchange (= overlap) integral
(Fig.28) RAB = internuclear distance of H2, a0 = Bohr radius.

The upper figure shows various formulas for calculating Coulomb integral (= ① ) and exchange integral (= ②, ③ ) between two electrons used in quantum mechanical H2 molecular calculation ( this p.5, this p.13, this p.16, this p.19, this p.3 ).
RAB is the distance between two nuclei of hydrogen atom HA and hydrogen atom HB in H2 molecule.
r12 is the distance between electron-1 and electron-2.
a0 is Bohr radius = 0.529 Å
S = the overlap integral.
The most difficult integral is the exchange integral between two electrons (= ②, ③ integrals of Fig.28 ), which can Not be calculated analytically (= No simple integral formula ).
↑ Tha fact that even simplest H2 molecular calculation or integral is extremely difficult and time-consuming means quantum mechanical approximate methods are all useless and impractical in larger molecules.
We use two methods of calculating this most difficult exchange integral between two electrons; one is the simpler approximatite formula (= ② this Mulliken approximation = average of two Coulomb energy integral of electrons around the same nucleus and between electrons belonging to two different separate nuclei × S2 ), and another is more precise formula using unsolvable Euler exponential integral.
γ is called Euler constant ( γ = 0.57721566490153286 ).
Integral formulas of Fig.28 is the case of exponent parameter Z = 1.
So if you want to use Z > 1, you should replace Bohr radius a0 by a0/Z in the same way as Fig.13 formulas, as shown in comparison between the hydrogen 1s wavefunction of Z=1 and Z > 1.
(Fig.29) Simple JAVA program to compute H2 molecular energies. H2bond=H2 molecular bond attraction, H2anti=Pauli repulsive energy.

Next we actually compute H2 molecular attractive bond and Pauli repulsive antibond energies in various internuclear distance (= RAB ) and Z exponent parameters.
JAVA program to compute H2 molecular energies
When you copy and paste the above JAVA sample program to a text editor, you can easily compile and run it.
The class file name of this JAVA program is "hymol", so complie it as "hymol.java"
After running this program, you are asked to input the distance (= RAB Å or angstrom ) between two nuclei of hydrogen atoms HA and HB in H2 molecule. ← Here we input " 0.87 " (Å).
Next you are asked to input the exponent Z parameter of hydrogen-like 1s wavefunction. ← Here we input the simplest" 1 " (= Z ).
Then, you are asked to input Euler exponential integral E(-2r) = E(-2RAB/a0) and E(-4r) = E(-4RAB/a0) of Fig.28 ③ exchange integral.
If you want to know only the result of the approximate exchange integral (= ② of Fig.28 ), you just input "0" and "0" as Euler exponential integral E(-2r) and E(-4r).
When you want know the value of E(-2r), first, input -2r = -2RAB/a0 = -2 × 0.87 (= RAB )/0.529177 (= Å = a0 = Bohr radius ) = -3.288124767 into this Euler exponential integral calculator (= x ), put the execute button, which gives the result of "-0.00907280116" ← Input this value as E(-2r) in the above program.
And input -4r = -4RAB/a0 = -4 × 0.87 (= Å RAB)/0.529177 (= Å a0 Bohr radius ) = -6.5762495 into this Euler exponential integral calculator (= x ), put the execute button, which gives the result of "-1.8654667322e-4" ← Input this value as E(-4r) in the above program.
In the calculation result of the above program,
H2bond-appro-1 = -3.224095 eV is H2 molecular attractive bond energy (= energy change from the original two separate H atoms ) using the approximate exchange formula ② of Fig.28, and
H2bond-Euler = -3.155709 eV, which is also H2 molecular attractive bond energy using the Euler precise exchange formula ③ of Fig.28.
Experimental H2 molecular attractive bond energy is -4.7467 eV at 0.741 Å internuclear distance.
This calculation result of H2 molecular attractive bond energy = -3.15 eV at the internuclear distrance RAB = 0.87 (= when Z = 1, this is the lowest and most stable bond length when using two H atomic wavefunctions with Z = 1 as chosen H2 molecule trial wavefunction ) is compatible with other sites' results ( this, this p.22, this p.4 ).
H2anti-appro-1 = +7.198067 eV and H2anti-Euler = +7.008849 eV are H2 Pauli repulstive antibond energy (= change from the original two separate H atoms ) using the exchange integral of approximate ② and Euler's rigorous ③ formulas of Fig.28.
Other output results are
Overlap integral (= S ) = 0.684880.
Coulomb potential between two nuclei (= separated by 0.87 Å ) = +16.5513 eV.
Coulomb (attractive energy) between electron and the other nucleus = -14.9179 eV (= using ② formula of Fig.13).
Coulomb integral (= repulsion ) between two electrons = +12.8272 eV (= using ① formula of Fig.28 )
Exchange integral between electron and nucleus = -13.9000 eV (= using ③ formula of Fig.13).
Exchange integral between two electrons-approxi-1 = 6.9970 eV (= using ② formula of Fig.28)
Exchange integral between two electrons (euler) = 7.0975 eV (= using ③ formula of Fig.28)
From these computed values, we can know Coulomb potential energy change without exchange energy in this H2 molecule.
Coulomb potential energy change in H2 molecule (= when internuclear distance = 0.87 Å Z = 1 ) becomes +16.5513 eV (= internuclear potential ) - 2 × 14.9179 eV (= 2 × Coulomb attraction between two electrons and the other nuclei ) +12.8272 eV (= Coulomb repulsion between two electrons ) = - 0.4573 eV which is far less influential than the exchange-energy-dependent molecualr bond energy = - 3.1557 eV in the upper figure.
Coulomb energy-based bond of H2 molecule using quantum mechanical spreading H atomic wavefunction or electron cloud is too weak (= only -0.4573 eV ) compared to actual H2 molecular bond energy (= -4.7467 eV at 0.741 Å internuclear distance, or the above calculation result of two simple H atomic wavefunctions = -3.155 eV at 0.87 Å internuclear distance ).
↑ This means quantum mechanical H2 molecular attractive bond energy heavily relies on unphysical exchange energy manipulating pseudo-kinetic energy.
The last output of "H atom energy increase by Z contraction (eV) = 0.000" is not used in the case of Z = 1
(Fig.30) When internuclear distance RAB = 2 × 0.87 Å = 1.74 Å

Next, after running this program, we input " 1.74 (= Å) " as internuclear distance RAB, which is twice as long as Fig.29 to know whether Pauli repulsive antibond energy at this distance is strong enough to prevent unreal H3 molecular bond by overcoming molecular attractive bond energy = -3.16 eV at 0.87 Å distance between two adjacent H atoms.
We input the exponential parameter Z = 1, Euler exponentical integral E(-2r) = -1.8654667322e-4 and E(-4r) = -1.37733687e-7.
↑ Euler exponential integral E(-2r) = -1.8654667322e-4 can be obtained by inputting -2RAB/a0 = -2×1.74(= Å )/0.529177(= Å = Bohr radius ) = -6.5762495 into this site's x and click execute button.
Euler exponential integral E(-4r) = -1.37733687e-7 can be obtained by inputting -4RAB/a0 = -4×1.74(= Å )/0.529177(= Å = Bohr radius ) = -13.15249907 into this site's x and click execute button.
At this internuclear distance RAB = 1.74 Å (= 2 × 0.87 Å of Fig.30 ), H2 Pauli repulsive antibond energy becomes very weak = +0.694278 eV (= obtained using approximate formula ② of Fig,28 ) or 0.675311 eV (= obtained using Euler formula ③ of Fig,28 ).
If you compare H2 molecular strong attractive energy = -3.1557 eV at the internuclear distance of 0.87 Å (= between two adjacent H atoms with the opposite spins ) of Fig.29 and weak Pauli repulsion of only +0.6753 eV at the internuclear distance of 1.74 Å (= between two H atoms with the same spin which are two atoms away from each other) of Fig.30, we find that quantum mechanical Pauli repulsion based on antisymmetric wavefunction cannot stop unreal H3 molecular covalent bonds.
Hence, quantum mechanics is false.
(Fig.31) Spin-up-spin-down = strong attraction (= -3.16 eV at 0.87 Å distance ), spin-up-spin-up weak Pauli repulsion (= 0.68 eV at 2 × 0.87 Å = 1.74 Å ) ↓

According to quantum mechanical Pauli principle, when two electrons have the opposite spins up and down (= parallel, antisymmetric, singlet spin ), the spacial H2 wavefunction becomes symmetric causing strong molecular bond attraction (= lowering total energy ) through the unphysical kinetic exchange energy decrease or constructively-interfering wavefunction.
As shown in Fig.29, this molecular bond attractive energy based on the constructive symmetric wavefunction with up-down spins becomes -3.15 eV at the H2 bond length RAB = 0.87 Å (= between two adjacent H atoms with the opposite spins )
To stop unreal H3 molecular bond formation, the left-side H atom with up-spin electron has to stop the 3rd H atom with the same up-spin electron at the right side, which is two atoms away, from bonding to the middle 2nd H atom with spin-down electron ( this p.9 ).
The distance (= 1.74 Å = 2 × 0.87 Å ) between the left-side and right-side H atoms with the same spin is twice longer than the distance (= 0.87 Å ) between middle and right-side H atoms with the opposite spins.
↑ This Pauli repulsion by antisymmetric wavefunction between the left and right-side H atoms with the same-directional spin is very weak = only 0.67 eV as shown in the last of Fig.30.
As a result, the right-side 3rd electron can safely form attractive covalent bond with the middle H atoms with the attraction = -3.15 eV (= symmetric bond energy ) + 0.67 eV (= Pauli repulsive antibond energy ) = -2.48 eV.
In the same way, the 4th H atom with spin-down can bond to the 3rd H atom with spin-up with the attractive energy = -2.48 eV.
The sum of the 3rd and 4th H atomic attractive bond energy becomes 2 × -2.48 eV = -4.96 eV, which is stronger than the experimental H2 covalent bond energy (= -4.75 eV, this p.22-last ), which means unreal H4 molecule formation is allowed in quantum mechanical Pauli antisymmetric wavefunctions.
This results show quantum mechancs is false, because its Pauli principle cannot stop unreal H3,H4,H5.. molecular bond formation.
(Fig.32) JAVA program to compute H2 molecular energy ( Z = 1.166 ) at two H atomic internuclear distance RAB = 0.743 Å

After running this program, we input " 0.743 (= Å = internuclear distance RAB )" and " 1.166 (= exponent parameter Z )"
And we input Euler exponentical integral E(-2r) = -0.009231331 and E(-4r) = -1.9250486088e-4
E(-2r) = -0.009231331 can be obtained by inputting -2×0.743 (= Å ) × 1.166 (= Z ← due to Bohr radius a0 replaced by a0/Z ) /0.529177 (= Å Bohr radius ) = -3.274284408 into this site's x and clicking execute button.
E(-4r) = -1.9250486088e-4 can be obtained by inputting -4×0.743 (= Å ) × 1.166 (= Z ) /0.529177 (= Å Bohr radius ) = -6.548568815 into this site's x and clicking execute button.
H2 molecular attractive bond energy = -3.78 eV at molecular bond length RAB = 0.743 Å ( Z = 1.166 ) agrees with other sites ( this p.3, this 1.10.8, this p.2-table1, this table3 where energy (-1.139+1) × 27.2 eV = -3.78 eV ), and slightly disagree with experimental value of -4.74 eV at 0.741 Å
↑ But as I said, these so-called "average" or "expectation" energy values obtained by integration instead of solving Schrödinger equation are Not true energies based on true wavefunctions, because the total energy conservation law is violated inside a H2 molecule.
(Fig.33) H2 molecular bond length = 1.488 Å, exponent Z = 1.166

As shown in Fig.31, the quantum mechanical Pauli repulsion expressed by antisymmetric wavefunction is too weak to stop H3, H4, H5.. molecular bond formation in the case of the exponent parameter Z = 1.
Here we prove quantum mechanical Pauli repulsion is Not strong enough to stop unreal H3 molecule in the variational exponent parameter Z = 1.166, either.
After running this program, we input " 1.486 (= Å internuclear distance = 2 × 0.743 Å )" and the variational exponent parameter Z = " 1.166 ".
Then, input Euler exponential integral E(-2r) = -1.9250486088e-4 and E(-4r) = -1.461504e-7
E(-2r) = -1.9250486088e-4 can be obtained by inputting -2×1.486 (= Å ) × 1.166 (= Z ) /0.529177 (= Å Bohr radius ) = -6.548568815 into this site's x and clicking execute button.
E(-4r) = -1.461504e-7 can be obtained by inputting -4×1.486 (= Å ) × 1.166 (= Z ) /0.529177 (= Å Bohr radius ) = -13.0971376 into this site's x and clicking execute button.
At this internuclear distance RAB = 1.486 Å (= 2 × 0.743 Å ), Pauli repulsive antibond energy becomes 2.01 eV which is weaker than molecular bond attractive energy = -3.78 eV in Fig.32. ← Quantum mechanical Pauli repulsion is too weak !
When using the exponent parameter Z = 1.166 in hydrogen-like atomic 1s wavefunction which hydrogen wavefunction is contracted and increasing kinetic and total energies than the original non-contracted hydrogen wavefunction (= Z = 1 ) by +0.3749 eV.
↑ You can get this value by running this program, inputting large internuclear distance (ex. 8.0 Å ) and Z = 1.166, and see H2 bond energy = 2 × +0.3749 eV = 0.749 eV (= each contracted H atomic energy with Z = 1.166 originally increases by +0.3749 eV by default even when two H atoms are very far away from each other and Not interacting ).
When putting the 3rd H atom from the right side toward the two already-contracting H2 molecule, you count this increased energy by contracted H atom more times than necessary,
When the 3rd H atom with up-spin bonds to the middle H-atom with down-spin of the already-existing H2 molecule (= already-shrinking by Z = 1.166 ), the bond attractive energy = -3.784 eV ( ← in this case, we counted the increased energy (= + 0.3749 eV ) by contracted H atom twice in the middle H atom, so we need to subtract the increased energy 0.3749 eV of the middle H atom which is already contracted and counted ).
And when calculating Pauli repulsive antibond energy (= +2.017 eV) between the left and right H atoms with the same spin, we have already counted all three H atomic increased contraction energy = +0.3749 eV in calculation of molecular attactive bonds, so we need to subtract 2 × +0.3749 eV contraction energy of lef-side and right-side H atoms from this Pauli repulsive energy calculation.
As a result, the 3rd H atom with up-spin can safely bind to the middle H atom with down-spin forming unreal H3 molecule by strong attractive energy = -3.784 + 2.017 - 3 × 0.3749 eV = -2.891 eV.
In the same way, the 4th H atom with down-spin can bind to the 3rd H-atom to form unreal H4 molecule by attractive energy stronger than -2.891 eV.
↑ The sum of these molecular attractive energies is 2 × 2.891 eV = -5.782 eV which is stronger than experimental H2 molecular bond energy = -4.75 eV ( this p.22-last ).
↑ This means if quantum mechanical Pauli antisymmetric rule is right, unreal H3,H4,H5.. molecules binding many H atoms are possible, which proves quantum mechanics is wrong.
(Fig.34) if the exponent parameter is Z = 1.166, the contracted H atom energy increases by +0.3749 eV from the original H atom with Z = 1
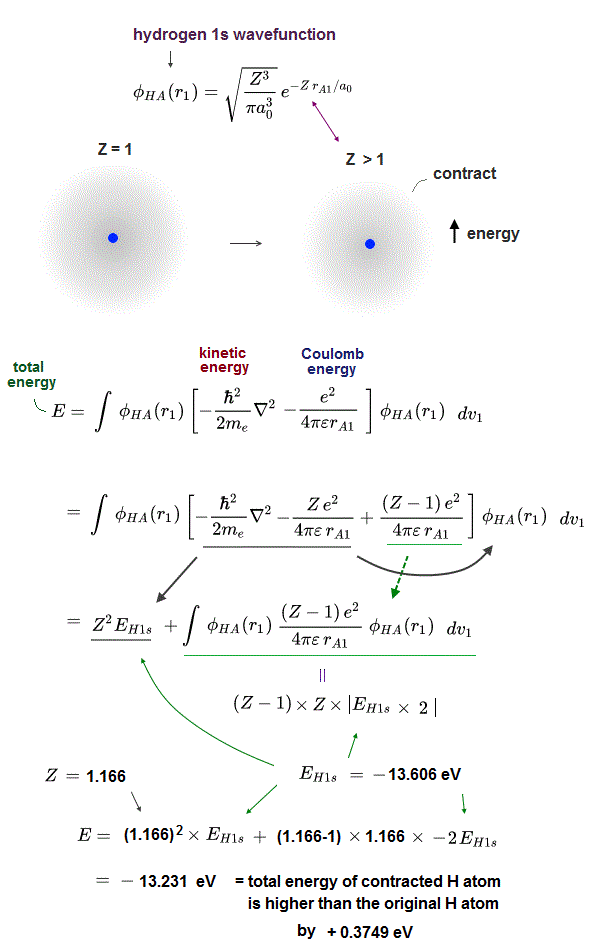
As shown in Fig.23, when we want to use the contracted H atomic 1s wavefunction with the exponent parameter Z > 1 around the same Z = +1 positive H atom nucleus, the total energy of this contracted H wavefunction increases by increased kinetic energy through contraction (= contracted H atom = larger curvature → shorter de Brolgie wavelength → increasing kinetic energy ).
For example, when we use the contracted H atomic 1s wavefunction with Z = 1.166, this contracted wavefunction's total energy is 0.3749 eV higher than the non-contracted original H atomic wavefunction with Z = 1.

2022/5/10 updated. Feel free to link to this site.