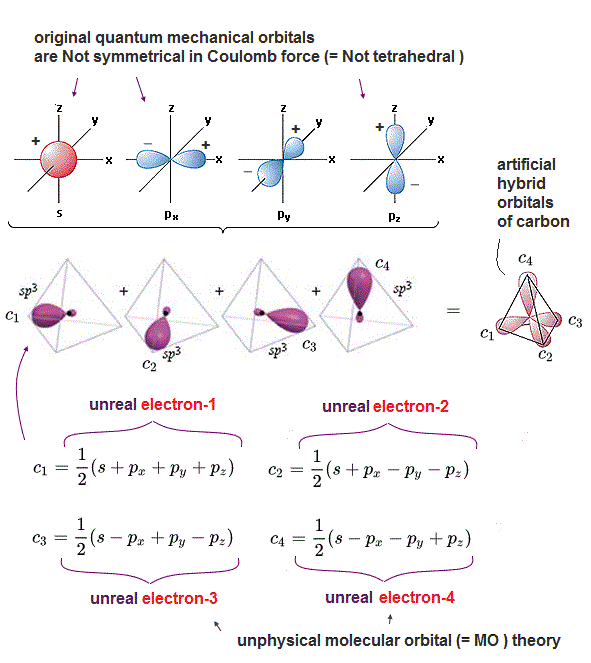
(Fig.1) Quantum mechanical artificially-created hybrid orbitals do Not consider real Coulomb force, even if their ad-hoc sp3 "tetrahedral" orbitals look symmetrical.

Four valence electrons of a carbon atom are distributed in symmetrical tetrahedral arrangement satisfying the balanced symmetrical Coulomb electric repulsions among four valence electrons of a carbon.
But the original quantum mechanical orbitals of a carbon obtained by solving Schrödinger equation of a hydrogen atom are Not tetrahedrally symmetrical as seen in 2s, 2px, 2py, 2pz orbitals ( this p.2-upper ).
So the unscientific quantum mechanics and its pseudo-atomic model called molecular orbital (= MO ) theory try to artificially create the so-called (ad-hoc) "hybrid" pseudo-orbitals by combining the original non-symmetrical s and p orbitals.
↑ This artificial manipulation shows that quantum mechanics itself is unable to naturally give the real atomic orbital shape based on Coulomb electric force (= the only calculation tool of quantum mechanics, Schrödinger equation gives unsymmetrical non-tetrahedral orbitals ).
These four artificially-created hybrid tetrahedral orbitals of a carbon are called "sp3 orbitals ( this p.10 )" which ad-hoc pseudo-orbitals are Not obtained from solving Schrödinger equation, because No multi-electron Schrödinger equations can be solved.
Each sp3 hybrid orbital consists of four original (hydrogen) atomic orbitals of s,px,py,pz with plus (= +px, +py, +pz ) or minus (= -px, -py, -pz ) wave phases.
The opposite plus and minus wavefunction's phases are supposed to cancel each other by destructive interference, while the same wave phases (= plus+plus or mimus+minus ) increase each other's probability amplitude by constructive interference.
Quantum mechanical molecular orbital theory unreasonably claims that each single electron must always spread over all the four different atomic orbitals as the artificial (sp3) hybrid orbitals whose states lack physical reality ( this p.1-right-argument ).
For example, in one of sp3 orbitals = c1 hybrid orbital, an electron-1 must be split into four smaller pieces and spread over all four orbitals s, px, py, pz orbitals, unrealistically.
(Fig.2) Quantum mechanical artificial rule = normalization & orthogonal.

Each ad-hoc hybrid molecular or atomic orbital must contain the same amount of electronic charge probability = one electron.
So the integral of the square of each hybrid wavefunction (= electron probability equals the square of its wavefunction amplitude ) must be always "1", which condition is called "normalization".
Furthermore, quantum mechanical Pauli exclusion principle expressed as the unphysical antisymmetric wavefunction or Slater determinants ( this p.4-5 ) have fatal flaws ( this p.5-6 ).
These unphysical antisymmetric wavefunctions imposed by quantum mechanics for no legitimate reason generate the unphysical exchange energies which are the (illusory) driving force of strong Pauli repulsive energy or molecular attractive energy in quantum mechanical molecules, depending on the sign ± of the exchange energies.
↑ But the spin integration of the opposite up and down spin wavefunctions always becomes zero ( this p.20 ), hence, quantum mechanics cannot generate any molecular attractive bond energy (= which is supposed to occur between electrons with the opposite spins ) expressed by the exchange energy or integral due to the zero spin integral between the opposite spins ( this p.5 ).
And only the unneeded Pauli repulsion expressed as the unphysical exchange energy or integral of the same spin (= up-up or down-down spins ) wavefunctions remains ( this p.29-30, this-(18.2.5) ), because the spin integral of two same spins does Not become zero unlike the zero spin integral of the opposite spins in exchange integral.
To avoid this paradox, quantum mechanics demands that all ( Pauli ) exchange energies or exchange integrals of two different molecular or atomic orbitals must be zero, which ad-hoc paradoxical condition is called "orthogonal ( this p.14-15, this p.1, this last, this p.12 )" or "orthonormal ( this p.2 2-3 paragraphs, this p.44-lower, this p.15 )".
The original four atomic orbitals such as 2s, 2px, 2py, 2pz are orthogonal to each other ( this p.13, this p.2 ), which means the exchange (or overlap, resonance ) integrals of these two different orbitals become zero like ∫ px py = 0 ( this p.7, this p.3 ).
As shown in the above figure, all the exchange integrals of four hybrid sp3 orbitals are zero or orthogonal like ∫c1c2 = 0. ← Just artificial rule imposed by defective quantum mechanics irrelevant to our real world phenomena.
(Fig.3) Exchange integral between two different sp3 orbitals (= ∫c2c3 ) becomes zero. = orthogonal. = artificial rule
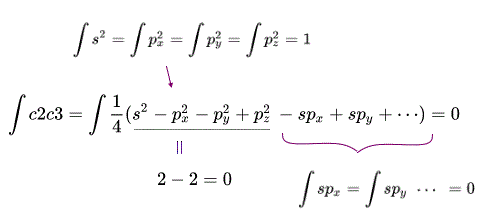
Using this this condition, we can prove exchange (= or overlap ) integrals between any two different sp3 orbitals of a carbon become zero.
The upper figure shows the exchange integral of two c2 and c3 sp3 orbital becomes zero, which artificial condition of molecular orbital theory is called "orthogonal" required for avoiding unneeded Pauli repulsive exchange energy.
(Fig.4) One H atomic 1s orbital bonding to 2pz orbital of carbon cannot be orthogonal to another 2s orbital, ← Unneeded Pauli repulsion occurs in MO C-H bond.
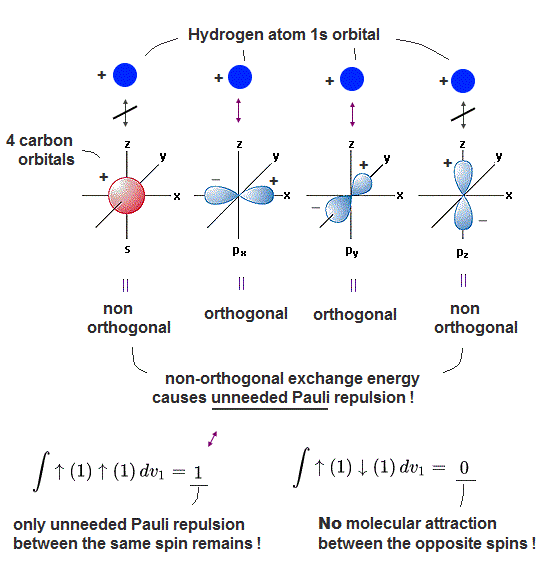
In fact, quantum mechanical carbon atom cannot bond to hydrogen atom to form the normal molecular attractive C-H bond due to unneeded Pauli repulsion between different molecular orbitals.
So quantum mechanical molecular orbital theory cannot explain molecular bonds such as methane (= CH4 ) with four single C-H bonds.
In the upper figure, one external hydrogen atomic 1s orbital (= H1s ) forms a single C-H bond with 2pz (or 2s ) orbital of a carbon atom.
In this case, this hydrogen atomic orbital cannot be orthogonal to another 2s (or 2pz ) orbital, hence, unneeded Pauli repulsion between these non-orthogonal orbitals breaks the original C-H molecular bond. → unstable molecule
H 1s orbital (= plus+ phase ) can form the hybrid molecular bond orbital with plus phase (+) of 2pz carbon's orbital (= one electron molecular orbital wavefunction is supposed to consist of the sum of the superimposed H1s + 2pz orbitals in MO theory ).
This H1s orbital (= + ) are orthogonal to other 2px and 2py orbitals, because plus and minus (= ± ) phases of px and py cancel each other and become zero in their exchange integral.
But the exchange integral between the remaining 2s orbital (= s orbital with plus+ phase ) and H1s plus+ phase does Not become zero (= non-orhogonal ), hence, the excessive Pauli repulsion occurs between this C-H bond (= between H1s + 2pz ) and the 2s orbital.
As a result, this molecular orbital theory cannot form the stable attractive C-H bond in methane.
This is one of fatal flaws in quantum mechanical molecular orbital (= MO ) theory.
And after all, the unneeded Pauli repulsion is impossible to eliminate especially in s orbitals, even if they try to artificially construct the nonphysical "orthogonal" hybrid orbitals.
(Fig.5) H1s-c1 hybrid orbital cannot be orthogonal to other c2-c4 sp3 orbitals. → Unneeded Pauli repulsion occurs.

Also in the artificial hybrid sp3 orbitals, the hyrogen H1s orbital bonding to c1 orbital cannot be orthogonal to other c2-c4 sp3 orbitals (= exchange integral between H1s and c2-c4 sp3 orbital is Not zero. ← unneeded Pauli repulsion is generated between these non-orthogonal wavefunctions ).
In the upper figure, one external hydrogen atomic H1s orbital bonds to one of sp3 orbitals = c1 orbital to form a new hybrid H1s-c1 molecular orbital (= one C-H molecular bond ).
The whole methane (= CH4 ) molecule contains the total eight valence electrons (= four H electrons + 4 C electrons ), so the methane needs at least four different molecular orbitals = each orbital can contain the maximum two electrons (= one electrons has up-spin, and another electron has down-spin ) due to Pauli principle rule.
These four ad-hoc molecular orbitals of the mathane are H1s-c1, H1s-c2, H1s-c3 and H1s-c4 tetrahedral hybrid orbitals, according to the familiar simple explanation which is wrong.
One of these new ad-hoc C-H bonds = H1s-c1 hybrid molecular orbital cannot be orthogonal to the remaining c2-c4 sp3 orbitals (= exchange energy or integral between this H1s and c2-c4 sp3 orbitals cannot be zero ), hence, unneeded Pauli repulsive exchange energies between this H1s and c2-c4 orbitals with the same spins (= each hybrid molecular orbital contains two electrons with up and down spins ) occurs and it makes this C-H bond unstable.
As shown in the upper figure, the sum of three c2,c3,c4 sp3 orbitals equals 3 × 2s orbital + the square root of 3 × 2p orbital.
The exchange (= or overlap ) integral between H1s orbital and this sum of c2-c4 sp3 orbitals are Not zero, which means non-orthogonal.
So basically, the familiar tetrahedral sp3 orbitals of a carbon cannot form stable C-H bonds of methane, which important flaw is often ignored in textbooks.
Of course, four H1s atomic orbitals are Not orthogonal to each other, which also cause unneeded Pauli repulsion.
(Fig.6). Each single electron must split into five different atoms (= C atom and 4 × H atoms ) in unreal molecualr orbital methane.
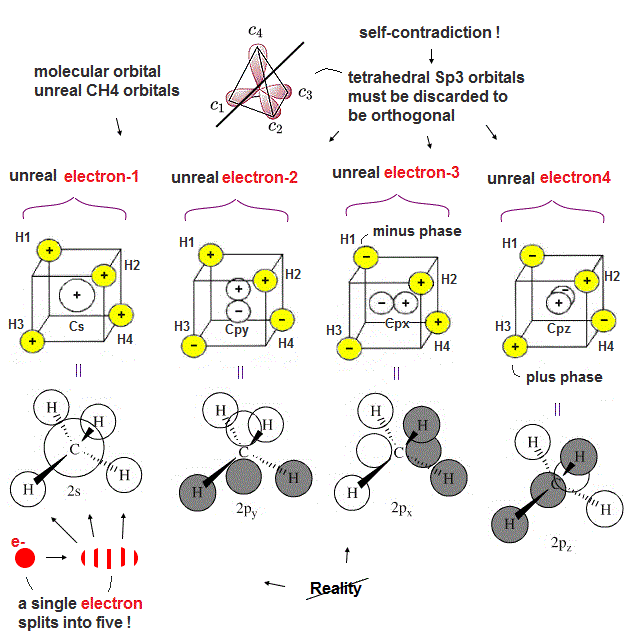
Familiar hybrid sp3 orbitals of quantum mechanics cannot form stable molecular bonds of methane (= CH4 ) due to non-orthogonality between the hydrogen atomic 1s wavefunction and four sp3 orbitals of a carbon atom.
To form orthogonal C-H bonds of methane, the quantum mechanical molecular orbital theory must unrealistically split each single hydrogen atomic electron into five smaller charges assigned to all four hydrogen atoms and one central carbon atom like the upper figure ( this middle, this p.1-lower-p.2, this-red square, this p.16 ).
The molecular orbital CH4 methane is unrealistic and completely different from the textbook's tetrahedral carbon's sp3 orbitals.
This unreasonable carbon's four molecular orbitals (= 2s, 2px, 2py, 2pz ) of the methane are Not tetrahedrally arranged = ignoring Coulomb repulsive force symmetry, so the quantum mechanical molecular orbital theory is a wrong molecular model.
(Fig.7) Exchange integral of (unreal) electron-1 and electron-3 of unphysical molecular orbital methane is zero.
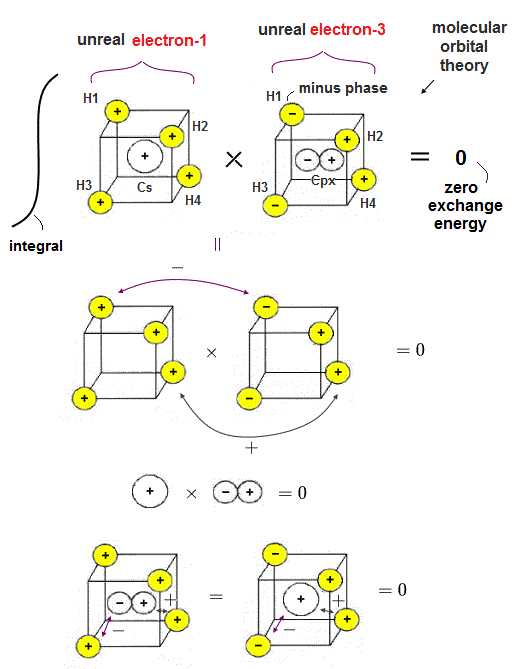
Exchange (or overlap ) integral of the unrealistic molecular orbital methane (= CH4 ) becomes zero whose artificial orthogonal molecular hybrid orbitals are obtained sacrificing "reality" by splitting a single electron into five smaller pieces.
For example, we consider the exchange integral of molecular orbitals between (unreal) electron-1 and electron-3 of methane.
In the upper figure, the total product (= exchange integral ) of four H atomic orbitals × four H atomic orbitals of (unreal) electron-1 and electron-3 becomes zero = 2 × (+-) + 2 × (++) = -2+2 = 0.
And the product (= exchange integral ) of the central 2s orbital of the electron-1 and 2px orbital of the electron-3 becomes zero.
The last part is the product (= exchange integral ) of four H atomic orbitals of the electron-1 (or electron-3 ) and the central carbon orbital 2px (or 2s ) of the electron-3 (or electron-1 ), which is also zero.
As a result, we can prove the (artificially-created) othogonality of the unreal molecular orbital methane.
But in fact, even if physicists try to artificially create unphysical "orthogonal" hybrid molecular orbitals seemingly eliminating exchange energies between hybrid orbitals, each hybrid orbital turns out to contain the same amount of Pauli exchange energies inside it, when they consider the nomalization (= each orbital contains the equal amount of electronic probability = 1 ), and the unneeded Pauli repulsion remains like in the original CH4.
Because whether the ad-hoc hybrid orbitals are othogonal or not, the same amount of equal electron's probability is distributed to four hydrogen atoms and four carbon atoms repelling each other by the same amount of unneeded Pauli repulsion.
Pauli repulsion (= antisymmetic or destructive interference ) means eliminating the overlapping region (= exchange overlap integral region ) by sharpening the wavefunctions or increasing kinetic energies.
↑ The orthogonal hybrid wavefunctions with zero overlap or exchange energy are just equal to wavefunctions after eliminating the overlap region by internal Pauli destructive interference. = unneeded Pauli repulsion remains, whether wavefunctions are orthogonal or not, hence, quantum mechanics is intrinsically false.
(Fig.8). Exchange integral of two (unreal) electrons spreading all over ethane is non-orthogonal = Not zero.
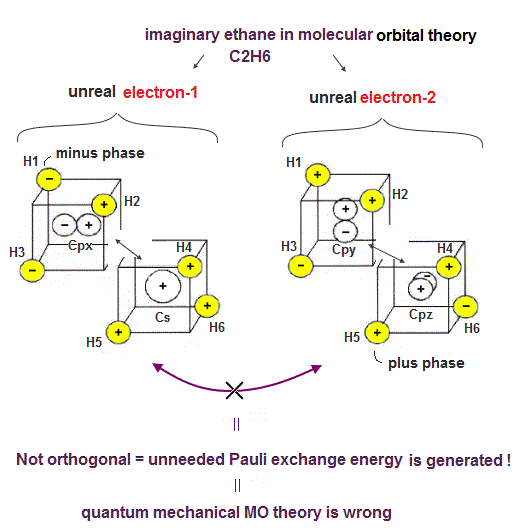
The problem is that this unrealistic molecular orbital theory cannot explain other molecules such as ethane (= C2H6 ).
Because unlike symmetrical methane (= CH4 ) consisting of four C-H bonds, the ethane consists of the odd-number seven bonds (= six C-H bond + one C-C ) bond which cannot cancel each other's unneeded Pauli repulsive exchange energy.
The number of ethane's valence electrons is 14 (= six H atoms + two C atoms with four valence electrons ), so at least seven different orbitals (= each orbital can contain the maximum two electrons with the opposite up-down spins ) are needed.
In the exchange integral of two ethane ad-hoc hybrid orbitals ( out of seven orbitals ) in the upper figure, the product (= exchange integral ) of six H atomic orbitals between the upper two unrealistic electrons's hybrid orbitals of the ethane is Not zero (= 2 instead of 0 ).
The product (= exchange integral ) of 6 H atomic electrons and two central carbon atoms between these two electrons's hybrid orbitals are Not zero, either.
This means the molecular orbital ethane causes the paradoxical unneeded Pauli repulsion, so wrong.
As shown in this middle, physicists gave up expressing the ethane as a combination of the original atomic orbitals such as 2s, 2p, H1s, instead, they try to escape into the vague σ or π bonds without showing the detailed atomic orbital pictures inside them.
Because of this fatal flaw of quantum mechanical molecular orbital theory, its only application = Huckel theory is a ad-hoc semi-empirical theory which must adjust free-parameters based on experimental results instead of predicting physical values.
Furthermore, this original molecular orbital Huckel theory could Not treat σ bonds such C-H and H-H bonds, instead, they are limited only to π bonds ( this p.1-3rd-paragraph ) relying on various artificially-adjusted parameters and rules with No power to predict any physical values.
The molecular orbital latest version, extended Huckel theory is also a useless semi-empirical theory which just artificially chooses free parameters from experimental values ( this p.1-lower ), and cannot predict any physical values from the theory itself ( this p.8-9 ), and the extended Huckel theory cannot treat the electron spin ( this p.2-2nd-last-paragraph, this p.4-5, p.18-19 ), which contradicts the original quantum mechanical theory.
In conclusion, quantum mechanics and its molecular orbital theory based on unphysical Pauli exchange energy failed due to their fatal flaws and inconsistent rules.
(Fig.8') Unreal ethane molecular orbitals have fatal flaws.
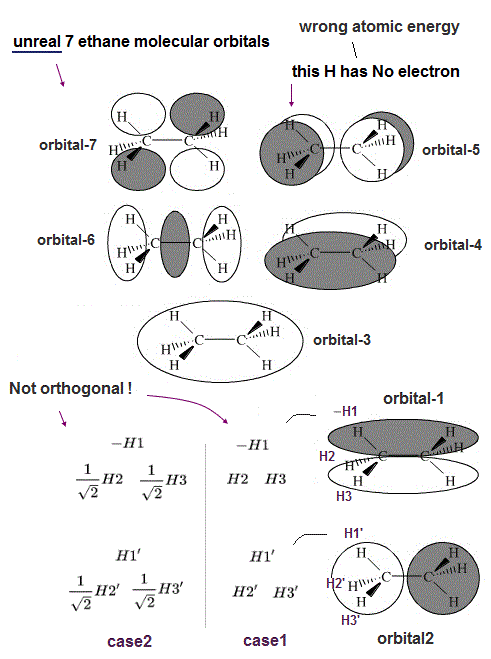
As shown in Fig.8, it's basically impossible to find the molecular orbitals of quantum mechanical ethane to satisfy the orthogonal condition, which means the unneeded Pauli repulsive exchange energy is always generated in most molecules such as ethane, invalidating the molecular orbital theory.
So the unscientific quantum mechanical molecular orbital theory gave up using the original atomic orbitals for constructing molecular orbitals such as ethane.
Ethane (= C2H6 ) has 14 valence electrons (= 2× 4 carbon valence electrons + 6 hydrogen atomic electrons ), so the ethane must have at least seven different hybrid molecular orbitals (= as shown in upper Fig.8' ) where each molecular orbital contains the maximum two electrons with up and down spins.
↑ Attractive exchange integral of two electrons with the opposite spins becomes zero, so only the unneeded Pauli repulsion occurs when "orthogonal" condition of zero repulsive exchange energy is not satisfied.
As shown in this this middle figure, quantum mechanics tries to apply ± phases similar to px,py,pz orbitals to the whole ethane hybrid orbitals including hydrogen 1s orbitals (= 1s orbital doesn't consist of ± phases unlike p orbital, so orhogonal condition is impossible to satisfy ), which idea causes a paradoxical and wrong result.
In the upper figure, the (imaginary) ethane's hybrid molecular orbital-1 includes three hydrogen atomic 1s orbitals (= -H1 with negative phase and H2,H3 with positive phase ) at the left side.
And another hybrid molecular orbital-2 of ethane includes three hydrogen atomic 1s orbitals (= H1',H2',H3' with positive phase ) at the left side.
In this case, the product (= exchange integral ) of these three H atoms of the orbital-1 and three H' atoms of the orbital-2 are Not zero (= in left and right sides ), hence non-orthogonal (= -H1×H1 + H2 ×H2 + H3 × H3 = + 1, Not zero ), which generates unneeded Pauli repulsion and the stable ethane molecular bond cannot be formed.
Even if we change the coefficient of H2 and H3 atomic orbitals into the square root of 2 like the upper figure-left-lower (= so that the total product of H1H1' + H2H2' + H3H3' = 0 ), the mixed product (= exchange integral ) of the orbital-1 and orbital-2 are Not orthogonal or not zero (= -H1H3' and -H1H2' cancel H1'H3 and H1'H2, but the exchange terms of H2H3' and H3H2' remains ).
Furthermore, in order to forcibly create unrealistic symmetrical dictribution in the odd-number three hydrogen atoms, these three hydrogen atoms must have different probabilities (= as shown in the upper figure, only H1 probaility amplitude is 1, and other H2 and H3 have the lower probability amplitude of 1/square-root of 2 ).
↑ The orbitals-4,5 in the upper figure cannot have H1 atoms, because a single H1 atomic 1s wavefunction (= positive phase ) cannot split into two ± opposite phases unlike p orbitals.
All six hydrogen atoms must have the same probability electron (= probability = 1 ) like each hybrid orbital also must have the same probability = 1 (= noramlization ), because each hydrogen atomic or hybrid molecular orbital is supposed to contain the same amount of electronic charge = one electron.
If each hydrogen atomic orbital contains different electron's probability or probability different from "1", those unrealistic hydrogen atoms become the impossible positive ions or negative ions, which drastically increase or decrease the total atomic energy, which disagrees with experimental results.
As a result, quantum mechanical ad-hoc molecular orbital theory collapses in almost all molecules such as ethane.
(Fig.9) Molecular orbital (= MO ) theory cannot explain any intermolecular attraction such as hydrogen bond and van der Waals attraction due to unneeded Pauli repulsion.

In unphysical quantum mechanical molecular orbital (= MO ) theory, physicists allegedly have to artificially construct the nonphysical hybrid orbitals which must be normalized and "orthogonal" to each other to avoid unneeded Pauli repulsive exchange energy.
But in fact, even in these ad-hoc "orthogonal" hybrid wavefunctions, they cannot eliminate unneeded Pauli repulsive exchange energy, which proves quantum mechanical molecular orbital theory is intrinsically false.
The upper figure is the case when the distance between two neutral hydrogen molecules (= H1 and H2 ) is about 1.7 Å, which is almost equal to the intermolecular distance causing weak hydrogen bond attraction, so any unneeded strong Pauli repulsion must be eliminated.
Due to the fatal flaw of quantum mechanical Pauli antisymmetric theory, they have to artificially construct the hybrid molecular orbitals orthogonal to each other, which means the exchange integral of two different hybrid orbitals must be zero, otherwise, only annoying Pauli repulsion remains with No molecular attraction based on the zero spin integral between the opposite spins.
Two hydrogen molecules contain four electrons with two up spins and two down spins, and two electrons with the same up-up or down-down spins cannot occupy the same orbitals, so the system of two hydrogen molecules needs at least two different hybrid molecular orbitals (= ψ1 and ψ2 ) which must be orthogonal to each other.
In the ad-hoc molecular orbital (= MO ) theory, each single electron must spread all over two hydrogen molecules H1 (= sum of two hydrogen atoms = φA + φB ) and H2 (= sum of two hydrogen atoms = φC + φD ).
↑ It means each electron's molecular orbital (= MO ) must be expressed as the linear combination of multiple atomic orbitals (= AO, this middle methane's four molecular orbitals, each orbital consists of four atomic orbitals of ± phases ).
Molecular orbital-1 ψ1 = N1 [ H1 + H2 ] = N1 [ ( φA + φB ) + ( φC + φD ) ] with smaller normalization coefficient N1, which can be obtained by normalization condition (= each molecular orbital contains one electron ) of ∫ψ1ψ1 = ∫N12[ H1 + H2 ]2 = 1
Molecular orbital-2 ψ2 = N2[ H1 - H2 ] = N2 [ ( φA + φB ) - ( φC + φD ) ] with larger normalization coefficient N2 > N1, which can be obtained by normalization condition of ∫ψ2ψ2 = ∫N22[ H1 - H2 ]2 = 1
↑ Each molecular orbital ψ1 or ψ2 contains two electrons up and down spins, and the electron with up-spin of ψ1 orbital and the electron with up-spin of ψ2 orbital cause the unneeded Pauli repulsive exchange energy (= and the unneeded Pauli repulsive exchange energy between the down-spin electron of ψ1 and the down-spin electron of ψ2 also occurs ), which must be zero by imposing the orthogonal wavefunctions = ∫H1H2 = 0
↑ But this orthogonal = zero exchange energy cannot eliminate the unneeded Pauli repulsion between H2 molecules-1 and 2 after all, because the unneeded Pauli repulsive exchange energy remains inside the ordinary Coulomb integral ∫ψ2ψ2 of the antibond orbital = ψ2 which is enhanced by its larger nomalization coefficient.
As shown in the upper figure, these two aritificial hybrid molecular orbitals satisfy the condition of normalization (= each hybrid molecular orbital must contain the equal amount of electron density or probability 1 like ∫ψ1ψ1 = ∫ψ2ψ2 = 1 ) and "orthogonal (= unneeded Pauli exchange integral must be zero like ∫ψ1ψ2 = 0 = overlap or exchange integral between two molecular orbitals ψ1 and ψ2 should be zero )."
Because of the negative exchange term (= Pauli repulsion ), the normalization coefficient of the molecular orbital (= ψ2 or antibond ) containing "negative term" becomes bigger than ψ1 containing only positive terms (= 1/(2-2S) > 1/(2+2S) where the overlap exchange integral S is an arbitrary value, in this intermolecular distance, S = 0.308, this p.5-6, this p.3, this p.11-12 ).
Hence, after all, the sum of total energies of ψ1 and ψ2 (= ordinary Coulomb integral = ∫|ψ1|2 + |ψ2|2 ) gives the strong unneeded Pauli exchange energy (= -2S^2/(1-S^2) =-0.681 S ), which unnecessary repulsion is big enough to prevent any weak intermolecular attraction such as hydrogen bond and van der Waals force. ← Quantum mechanics disagrees with experimental results.
The same contradiction is seen also in Helium (= He ) that allegedly cannot form He-He molecular bond due to the equal numbers of bond (= He+He ) and antibond (= He-He ) being generated ( this p.7,12 ).
But Helium is known to generate the weak van der Waals attraction between two Helium atoms. = the unneeded Pauli repulsion must be removed, but quantum mechanical molecular orbital theory cannot.
As shown above, this weak attraction between two Helium atoms is impossible in quantum mechanical molecular orbital theory where unneeded Pauli repulsion always occurs between two Heliums like two H2 molecules. = The antibond-Pauli repulsive energy is bigger than the attractive bond energy between two Heliums like two hydrogen molecules ( this p.3 ) after the normalization.
Pauli repulsion (= antisymmetic or destructive interference ) means eliminating the overlapping region (= exchange overlap integral region ) by sharpening the wavefunctions or increasing kinetic energies.
↑ The orthogonal hybrid wavefunctions with zero overlap or exchange energy are just equal to wavefunctions after eliminating the overlap region by internal Pauli destructive interference (= the negative overlap integral value -∫H1H2 of the square of the above antibond wavefunction ψ2 = N[ H1-H2 ] with the larger normalization coefficient N tacitly maintains the unneeded Pauli repulsive energy ).
↑ The unneeded Pauli repulsion remains, whether wavefunctions are orthogonal or not.
As a result, quantum mechanical molecular orbital theory, which cannot eliminate the unneeded Pauli repulsion after all, is a wrong theory.
Physicists have to rely on artificially-chosen fake potential energies irrelevant to the original quantum mechanics for molecular and intermolecular interactions. ← Quantum mechanics is contradictory.

2022/9/11 updated. Feel free to link to this site.