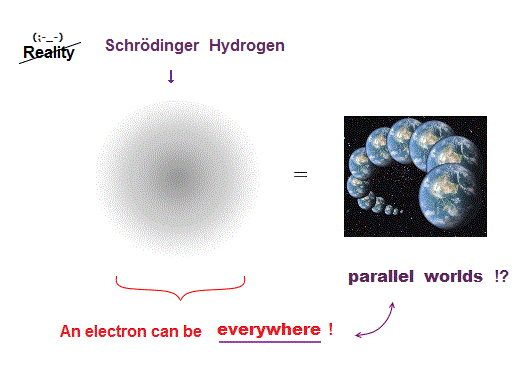
(Fig.1) Schrödinger's hydrogen = an electron everywhere !?

Quantum mechanics uses Schrödinger equation, where a single electron can be everywhere at the same time in parallel worlds.
Quantum mechanics tries to apply these unreal parallel worlds to all atoms !
But this "parallel-world" nature of Schrödinger equation does Not work in multi-electron atoms.
Here we prove quantum mechanics is wrong.
(Fig.2) Just vague electron cloud in quantum atom ↓

Quantum mehanics can not descibe real electrons.
It gives only vague electron cloud spreading over all space to infinity.
Strangely, though Schrödinger equation has kinetic energy, its electron is Not moving "realistically" !
This unphysical nature of quantum mechanics = "No clear electron, No electron's motion" causes serious problem in multi- electron atoms.
Because it's unreal.
(Fig.3) ↓ Only one-electron hydrogen has solution in quantum mechanics.
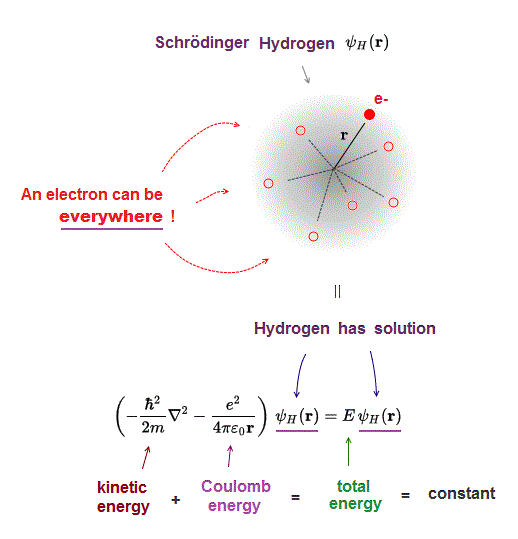
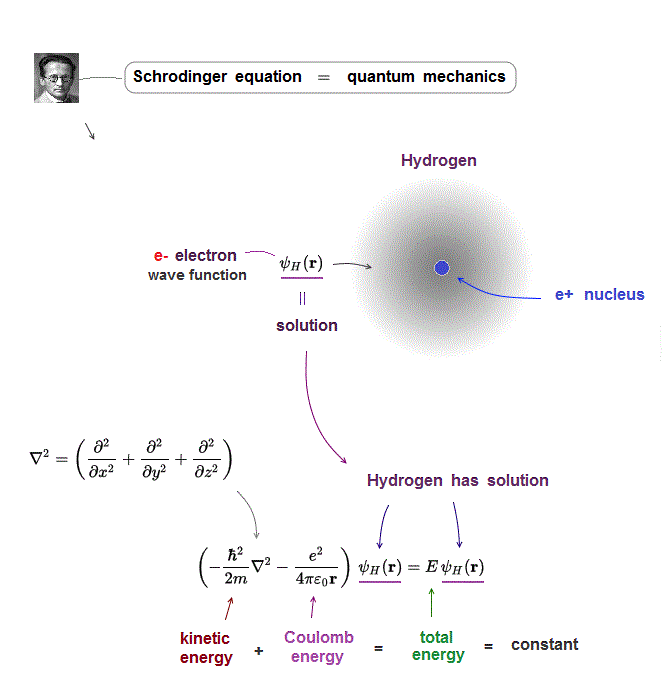
Only one-electron hydrogen atom has solution in Schrödinger equation.
Hydrogen wavefunction spreads all space, so in all space, the electron's total energy must be conserved at constant E.
Coulomb energy term must be cancelled out by kinetic energy to give constant total energy in all space.
This is impossible in multi-electron Schrödinger atoms.
(Fig.4) Two hydrogen wavefunctions → Helium ?
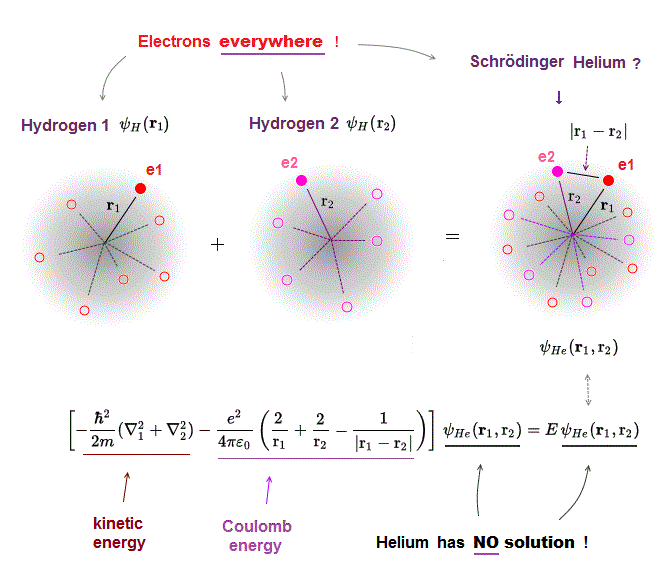
All Schrödinger equations for multi-electron atoms such as two-electron helium are known to be unsolvable.
Basically, quantum mechanics tries to waste time in choosing fake approximate solution or trial wavefunction as a fictitious helium wavefunction (= the simplest one is a fititious helium wavefunction consists of two hydrogen 1s atomic wavefunctions ) and integrating it to obtain fake average total energy E instead of solving the unsolvable Schrödinger equation for helium.
We can prove Schrödinger equations for multi-electron atoms such as helium can never find true solutions, no matter what fake trial wavefunctions are chosen.
This is due to the always-spreading probability wavefunction of quantum mechanics where a single electron must unrealistically exist everywhere regardless of the other electrons' positions.
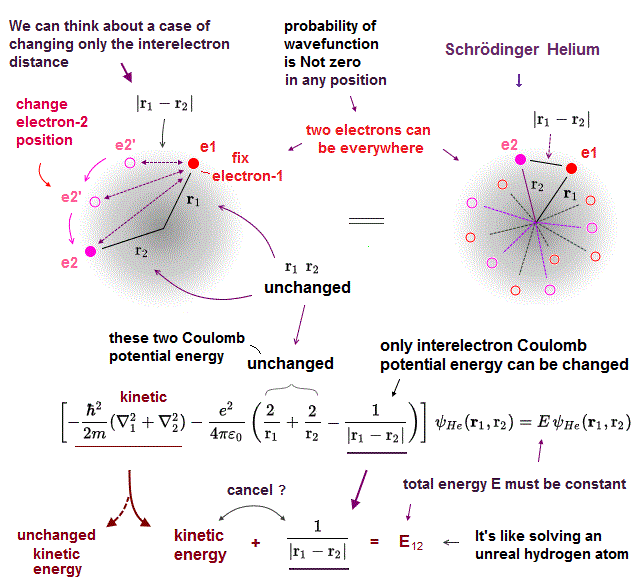
(Fig.5) ↓ Three Coulomb terms can be changed independently !?
Each single electron's probability wavefunction of quantum mechanics must always spread all over the place like a vague electron cloud with No boundaries.
Actually, the hydrogen atomic exact wavefunction obtained by solving its Schrödinger equation contains the exponential function which spreads out throughout the entire space to infinite points ( r → ∞ ).
Helium's approximate wavefunctions must also contain the exponential wavefunctions ( this p.2 ) whose electron's probability spreads all over the places (= electron's probabiliy can decrease or increase, but in No places the electron's probability becomes completely zero except for several node points ).
Because if the probability wavefunction suddenly discontinues and disappears at some point, the electron's kinetic energy term, which is equal to the derivative of wavefunction, unrealistically diverges to infinity (= kinetic energy differential gives infinite kinetic energies at the discontinuous wavefunction point where the slope is infinitely steep ).
To avoid such an unrealistic infinite kinetic energies, Schrödinger's probability wavefunction must always spread all over the place smoothly and continuously, as shown in the exponential wavefunction.
This unrealistic quantum mechanical probability wavefunction or spreading electron's cloud disproves quantum mechanics itself.
Schrödinger's equation for helium's two electrons (= e1 and e2 ) consists of two kinetic energy term expressed as the differential operators and three Coulomb potential energy terms ( this p.2 ).
These three Coulomb potential energy terms are Coulomb attractive energy between the electron-1 and the helium nucleus (= distance r1 ), Coulomb attractive energy between the electron-2 and the nucleus (= distance r2 ), and Coulomb repulsive energy between two electrons-1 and -2 (= distance |r1-r2| or r12 ).
In the upper figure, we can freely change the position of the electron-2 (= e2 in a circular way around the nucleus ) so that only the distance (= |r1-r2| or r12 ) between two electrons e1 and e2 is changed while other distance (= r1 ) between electron-1 (=e1 )-nucleus and the distance (= r2 ) between electron-2-nucleus are unchanged.
This means we can freely change only one Coulomb repulsive energy term between two electrons (= only e2/4πε |r1-r2| Coulomb energy can be changed ) while keeping other two Coulomb attractive energy terms unchanged (= = -e2/4πε r1 and -e2/4πε r2 are unchanged and fixed )
(Fig.5') ↓ Only one variable or distance r1 (or r2 ) can be freely changed in quantum mechanical helium atoms.
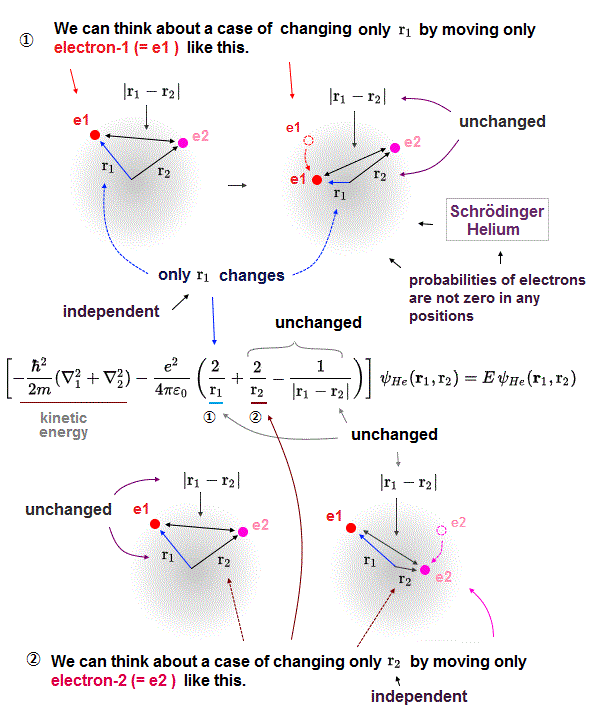
As shown in Fig.5', we can freely change only one variable or distance (= r1 ) between the electron-1 and the helium nucleus, while other distance variables (= r2 and |r1-r2 | ) are kept unchanged.
So in quantum mechanical helium, three distance variables and their three Coulomb energy terms are all free parameters changeable independently of the other two variables or Coulomb potential energy terms, which unscientific quantum mechanical atomic property causes serious problems, and disproves quantum mechanics.
(Fig.6) ↓ Helium = three unreal hydrogens ? ← Schrödinger is wrong !
For Schrödinger equations to have true solutions (= solvable ), the total energy E must be always constant and conserved in any electrons' positions by kinetic and Coulomb potential energy variables canceling each other, which is impossible in any multi-electron atoms such as Helium.
Quantum mechanical wavefunctions have to always spread out over all space as vague electron probability cloud.
Because if the wavefunction has discontinuous points, it causes electron kinetic energy expressed as derivative of wavefunction to be infinitely large.
So also in multi-electron atoms such as helium, the helium's two electrons' probability wavefunctions must always spread out over all space.
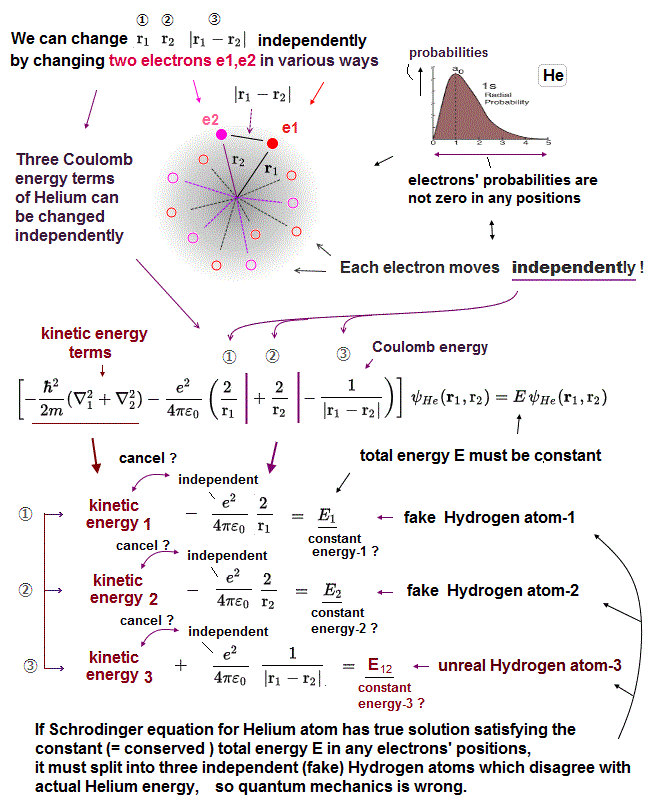
↑ The fact that the helium's two electrons's probabilities are not zero in any positions means three variables r1 (= distance between electron-1 and helium nucleus ), r2 (= distance between electron-2 and nucleus ), and |r1-r2| (= distance between the helium's two electrons ) can be changed independently ( this p.2 ).
So the helium's three Coulomb potential energy terms ( each term contains r1 or r2 or |r1-r2|) can also be changed independently depending on two electron's positions.
To cancel these three helium Coulomb potential energy terms' independent variables, the kinetic energy terms must also give three independent variable terms.
As a result, if Schrödinger equation for helium has true solution, it must consist of three (fictional) independent hydrogen-like atoms (= in each fictional hydrogen-like atom, its kinetic energy term must cancel its potential energy term to get the constant, conserved total energy E ).
The problem is these fictional hydrogen-like atoms must include the unrealistic hydrogen atom whose potential energy is the Coulomb repulsive energy (= 1/|r1-r2| ) between two electrons ( this-lower ③ ), which cannot have true solutions.
As a result, Schrödinger equations for any multi-electrons atom such a helium are unsolvable, and quantum mechanics proved to be wrong.
(Fig.H) Only Schrodinger equation for H atom has true wavefunction solution giving the constant total energy E in any electron's positions.
Only Schrödinger equation for one electron hydrogen atom is known to be solvable, which energy values "accidentally" agreed with Bohr's realistic hydrogen atom.
Total atomic energy E, which is the sum of electron's kinetic energy (= expressed as the second-order derivative ) and Coulomb potential energy, must be always constant and conserved.
In this solvable hydrogen atoms, we can find true wavefunction that gives the constant conserved total energy E in any electron's positions where variables of kinetic energy (= obtained by differentiating the wavefunction ) and Coulomb energy terms are canceled to give only constant E energy value ( this p.1-last, this p.2 ).
(Fig.6') Quantum mechanics is wrong, unable to find true solutions for multi-electron Schrödinger equations.
Unfortunately, No Schrödinger equations for multi-electron atoms such as helium are solvable.
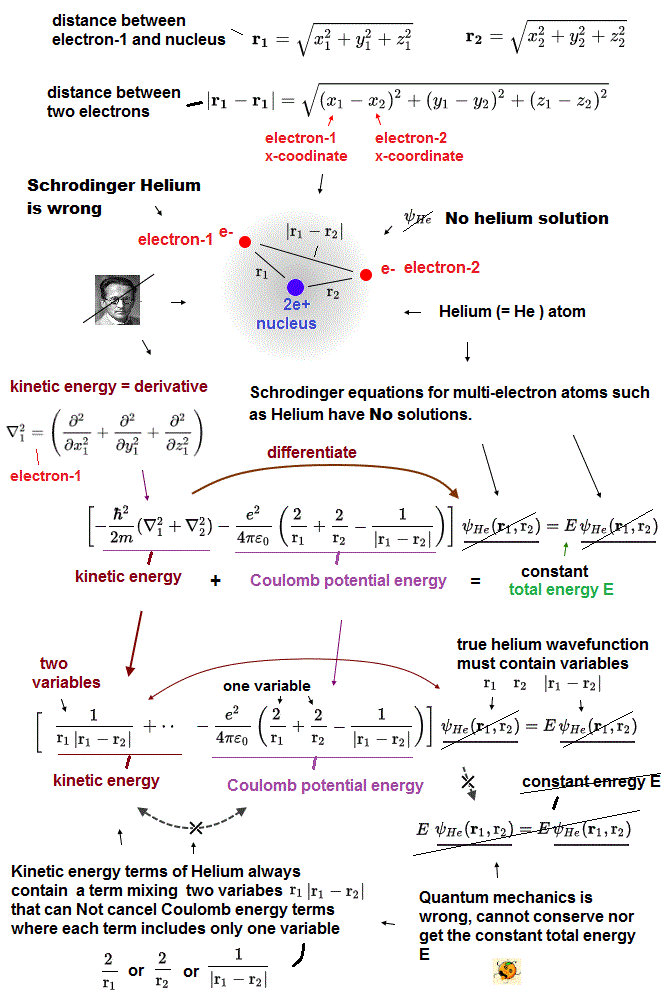
Helium wavefunction must contain three variables r1 (= distance between electron-1 and helium nucleus ), r2 (= distance between electron-2 and nucleus ) and |r1 - r2| (= distance between two electrons-1 and 2 ) for the kinetic energy terms (= obtained by differentiating the wavefunction ) to cancel the three variables of the helium Coulomb potential energy terms consisting of 1/r1, 1/r2, and 1/|r1 - r2| for getting the constant total energy E regardless of two electrons' positions of r1 and r2.
↑ This helium true solution can never be found, as shown in this and this, the helium kinetic energy terms (= obtained by differentiating the wavefunction ) always include a term mixing more than two variables of r1, |r1-r2| that can Not cancel variables of Coulomb energy (= each Coulomb energy term always consists of only one variable 1/r1 or 1/r2 or 1/|r1-r2| ).
As a result, Quantum mechanics or Schrodinger equations that can never find true solutions (= giving the constant conserved total energy E ) for any multi-electron atoms are proven wrong.
↑ Quantum mechanical (unrealistic) electrons' probability wavefunctions must always spread over all space (= if an electron is localized in only one point, whose acute de Broglie wavefunction drastically increases kinetic energy to infinity, giving wrong total energy ), so all Coulomb potential's variables must be completely canceled out to be zero by kinetic energy to get the constant conserved total energy E in all two electrons' positions, which is proven impossible, so quantum mechanics is wrong.
Only the realistic Bohr's helium atoms with two perpendicular orbits can give true helium's solution with the constant conserved exact total energy E in helium's two electrons' all positions (= Coulomb forces in any electrons' positions can be calculated by computers to conserve the constant total energy E in any electrons' positions along the orbits. )
If quantum mechanical Schrodinger equations have true solutions for multi-electron atoms (= which is impossible though ), the conserved total energy E must be constant in all multiple electrons' positions in all space, in which case, the realistic Bohr's helium atom conserving total energy in any two electrons' positions is also possible (= so Bohr's helium atom is definitely proven right, able to conserve the constant total energy in all electrons' positions along the orbits ).
(Fig.6'') Helium kinetic energy terms containing two variables cannot cancel Coulomb potential terms (= each term contains only one variable ), so Schrödinger equation for helium can never have true solution giving the constant conserved total energy E.
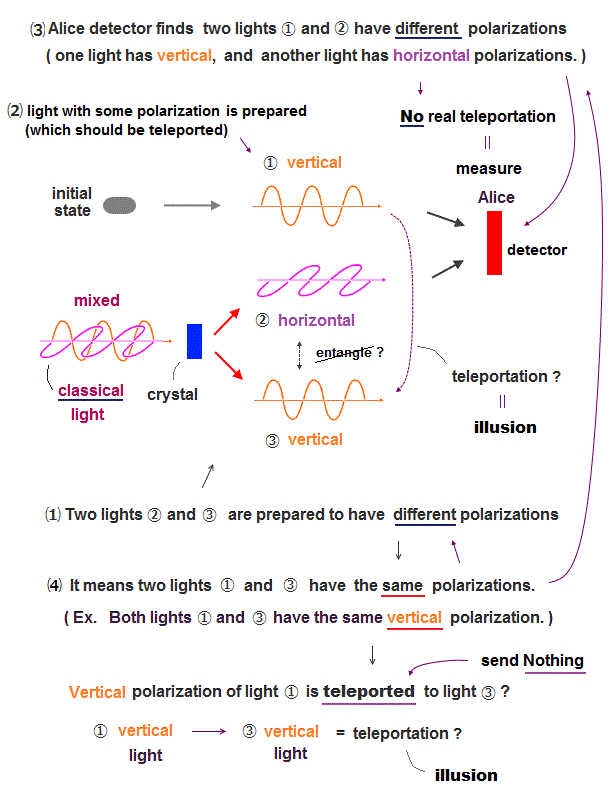
As shown in the upper figure, the helium kinetic energy terms (= second-order derivative ) always include terms consisting of two different variables of r1 and |r1-r2| (or r2, |r1-r2| ) which can Not be canceled by helium Coulomb potential energy terms where each Coulomb energy term consists of only one variable r1 or r2 or |r1-r2|.
In the upper figure, Schrödinger equation's kinetic energy (= derivative ) acts on exponential functions of some (chosen) Helium wavefunction's term of the highest order, which gives two-variable terms that cannot be canceled by Coulomb potential energy terms or by any other kinetic energy terms ( due to the highest-order term ). ← cannot get the constant conserved total energy E.
↑ These two-variable terms of kinetic energy cannot be canceled between x, y, z derivative terms due to two different variables (= x1, x1-x2 ) mixed
As a result, Schrödinger equations for helium or multi-electron atoms can never be solved nor have true analytical solutions, showing quantum mechanics is false.
(Fig.7) Each electron independent → Coulomb term independent → unreal atom
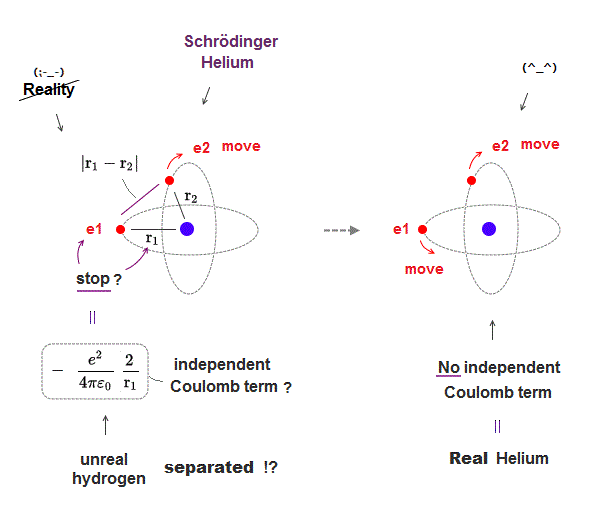
For Helium to be real, two electrons must move with time, dependently on another electron, which prevents each Coulomb energy term from changing independently.
If two electrons can move independently, each Coulomb energy term must be independent, which splits Helium into unreal three hydrogens, which doesn't exist.
This is the reason Schrödinger equation is wrong in multi-electron atoms such as Helium, and only classical orbits can give real Helium model.
But in old 1920s, there were No computers, so they couldn't handle three-body Helium electrons' motion classically, which is the reason only wrong Schrödinger equation survived.
(Fig.8) Simple model describing real atomic force is necessary.
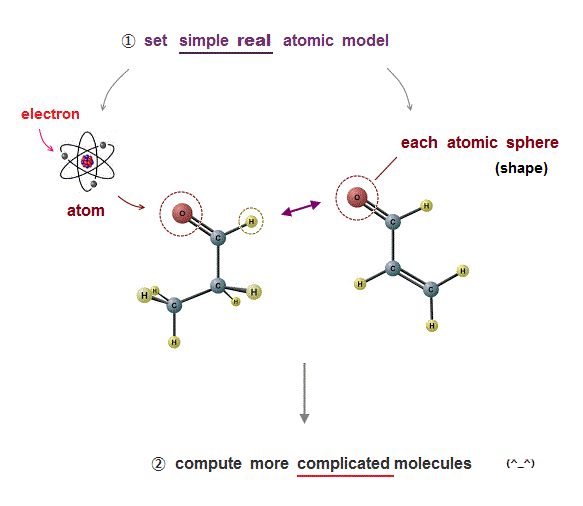
We need only two conditions to describe all realistic molecular behavior.
If there is only Coulomb relation condition, atomic (elecron orbital) radius is not determined.
de Broglie wavelength determines atomic size, and it can explain the different sizes between carbon and silicon.
These two conditions can explain the maximum electrons' number (= Pauli principle ) correctly, without unreal spin.
This simple atomic model (= only Coulomb + de Broglie ) can be easily applied to much bigger, complicated molecules with the help of computer to cure fatal disease.
(Fig.9) Simple useful model is impossible without real electrons.
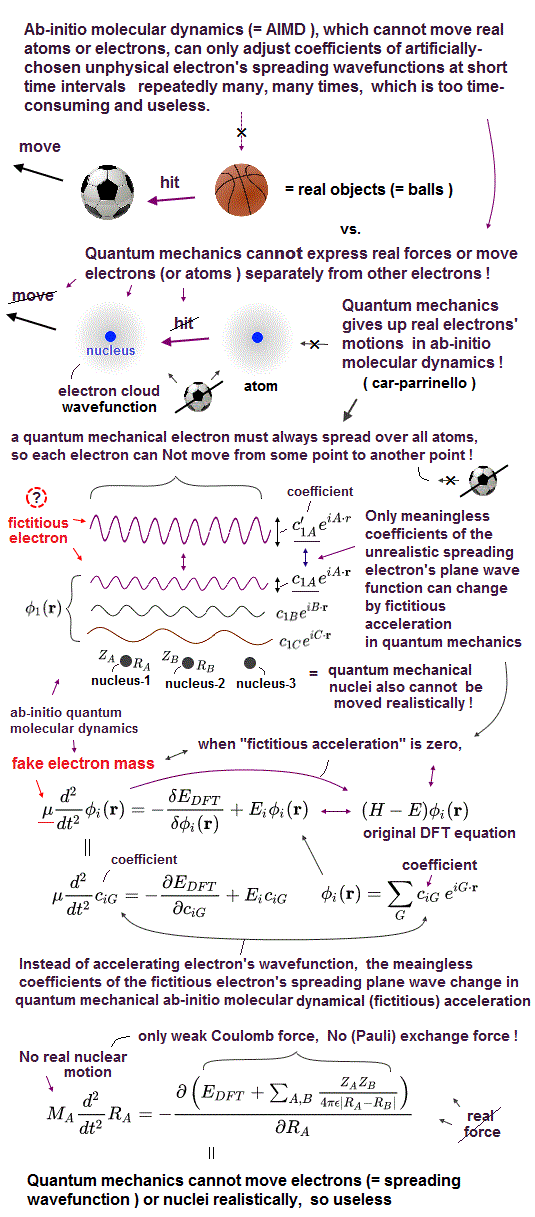
As I proved above, it is impossible to find exact solution in multi-electron atoms in Schrödinger equation.
Quantum mechanics just chooses artificial fake solution in each atom, which method is completely useless.
In applied physics, they use density functional theory (= DFT ), which also chooses artificial fake Coulomb energy term V.
Each time we deal with different atoms, we have to choose different artificial fake solution in vain.
This is the reason why quantum mechanics is useless forever in applied science such as medicine, and it lacks reality.
(Fig.10) Kinetic + potential energies = total energy E

Under the present science, Schrödinger equation in quantum mechanics is the only tool to calculate atomic energy.
Unfortunately, Schrödinger equation can solve only one-electron hydrogen atom, cannot deal with other multi-electron atoms.
Total energy E is the sum of an electron's kinetic energy and Coulomb potential energy in Schrödinger equation.
Of course, this total energy E must be conserved (= constant ) in every electron's position.
(Fig.11) ↓ Helium has No solution ( = No wave-function ψHe )

Schrödinger equation of Helium with two electrons cannot be solved (= Schrödinger Helium has No exact solution ).
Helium potential energy consists of three terms.
Two of them are Coulomb attractive energies between each electron and Helium nucleus (= -2/r1, -2/r2 in Fig.11 ).
The third term is Coulomb repulsive energy between two electrons.
It includes the variable r12, which represents the distance between two electrons.
(Fig.12) ↓ Helium approximate solution (= wavefunction )
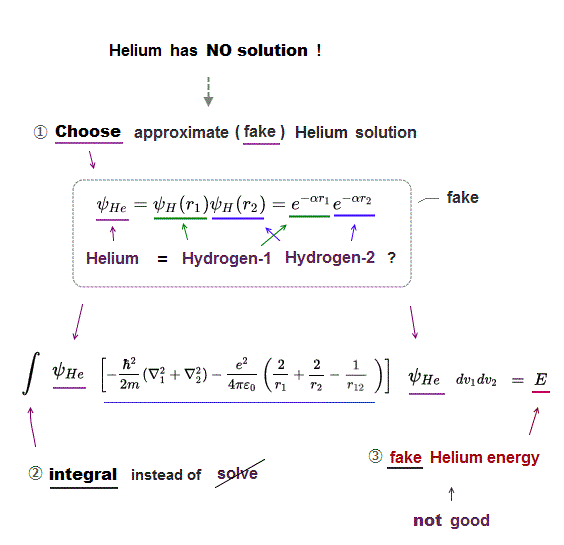
Schrödinger equation of Helium cannot be solved.
So we need to choose some approximate (= fake ) Helium solution (= trial wavefunction ).
Ths simplest Helium solution consists of two hydrogen atoms 1 and 2.
After choosing the fake Helium solution and inserting it into Schrödinger equation, we integrate it instead of solving it ( this p.2 ).
By adjusting parameter α, the total (fake) energy E can be lowered.
But this simplest Helium solution cannot get exact Helium energy ( this calculated energy E becomes -77.4 eV which is higher than actual Helium energy -79.0 eV, see this p.4 ).
(Fig.13) ↓ Hylleraas (fake) Helium wavefunction includes r12
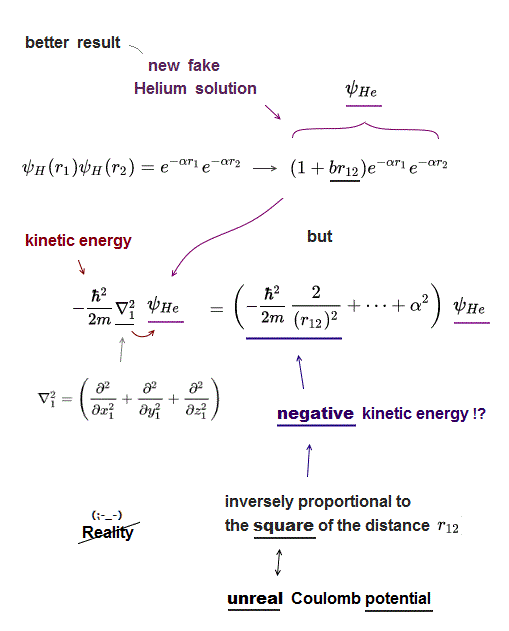
To lower the Helium total energy, quantum mechanics has to rely on wrong math trick, which proves quantum mechanics is wrong.
Instead of the simplest approximate Helium solution (= just two hydrogens ), they use Hylleraas Helium solution which is a little more complicated including r12 (= distance between two electrons ).
This new fake Helium solution including r12 gives better (= lower ) total energy than the simplest solution ( this new Hylleraas solution gives -78.7 eV of Helium total energy, this p.8, which is still slightly higher than the actual Helium energy ).
But in fact, quantum mechanics depends on wrong math trick when this new Hylleraas Helium solution is used.
Kinetic energy of Schrödinger equation is expressed as the second derivative.
This kinetic energy term always gives "unreal negative kinetic energy" which is inversely proportional to the square of distance between two electrons ( ~ 1/r122). ← this unusual term doesn't exist in the nature.
For the total energy to be conserved, the kinetic energy must cancel out the Coulomb potential energy which is inversely proportional to r12 (= 1/r12 ), Not to the square of r12 ( ~ 1/r122).
This is a wrong and unfair math trick, because the negative kinetic energy inversely propotronal to the square of r12 can unnaturally lower the Helium (fake) total energy in a wrong way.
Because it violates total energy conservation ( negative 1/r122 kinetic energy term cannot cancel Coulomb potential term 1/r12 ).
This is the trick by which quantum mechanics can seemingly get Helium energy value close to the experimental value.
But this deceptive quantum method sacrifices Helium total energy conservation (= kinetic energy + Coulomb potential energy cannot be constant E in this method )
Getting better energy value by deliberately violating total energy conservation (= lowering kinetic energy by dishonest method ) is physically false and inconsistent.
(Fig.14) ↓ Hydrogen 2p wavefunction.
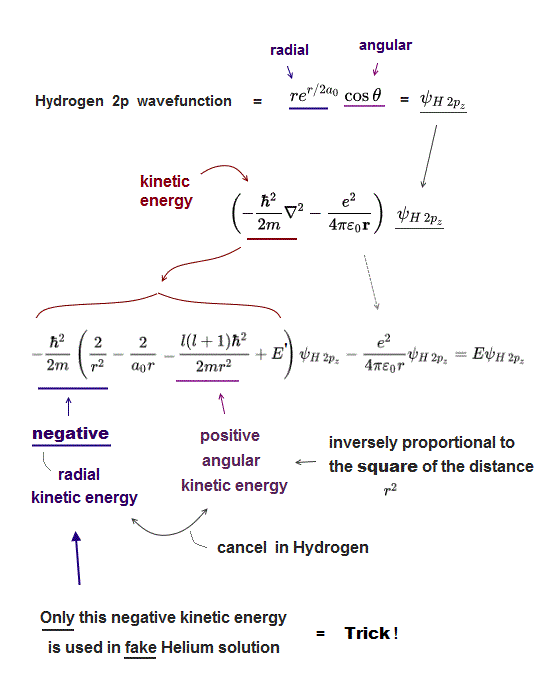
Unsolvable Schrödinger equation of Helium relies on "dirty trick" to lower its total energy using "negative kinetic energy" inversely proportional to the square of distance r12.
Because negative kinetic energy term inversely proportional to the square of distance (= -1/r2) can be lower than the term inversely proportional to the distance (= -1/r = Coulomb potential term ).
What's the origin of this nonphysical negative kinetic energy ?
This strange negative kinetic energy is necessary to cancel positive angular kinetic energy which increases inversely proportional to the square of distance (= 1/r2 ) in hydrogen 2p wavefunction.
Hydrogen 2p wavefunction consists of radial (= re-r ) and angular parts (= cosθ ). See this p.5 angular momentum l=1.
Kinetic energy (= second derivative ∇2 ) of the angular part (= cosθ ) in Hydrogen 2p wavefunction becomes inversely proportional to the square of distance (= l(l+1)/r2, see this p.5, this p.9 ).
For hydrogen total energy to be conserved (= E is constant ), this angular kinetic energy must be canceled out by corresponding negative kinetic energy inversely proportional to the square of r ( 0 = 1/r2-1/r2 ) in radial part.
Quantum mechanics uses only this radial part of negative kinetic energy in Hydrogen 2p wavefunction, omitting angular part (= spherical harmonics ) to lower Helium total energy in a dishonest way.
Of course, this Schrödinger Helium cannot conserve total energy E (= Not constant ), so physically wrong. This is the dirty trick of quantum mechanics, which is Not "successful" at all.

2018/8/20 updated. Feel free to link to this site.