Top (quantum mechanics and Einstein relativity are false )
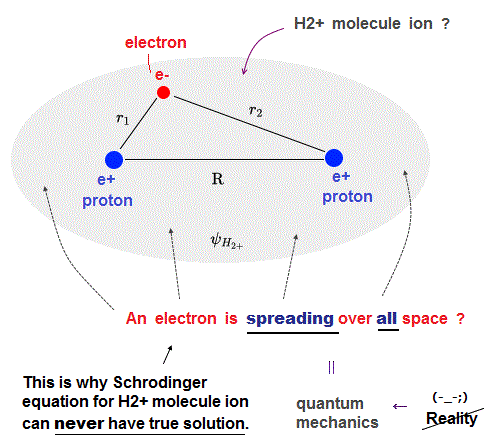
(Fig.1) ↓ Unrealistic Schrödinger equation for hydrogen molecule ion (= H2+ )

Contrary to the media-hype, quantum mechanical Schrödinger equation for hydrogen molecule ion (= H2+ ) cannot be solved analytically ( this p.2-3rd-paragraph ).
As shown in the hydrogen atomic wavefunction including exponential function (= e-r where the radial r is from zero to infinity ), all quantum mechanical (unphysical) atomic or molecular wavefunctions must always spread all over the place.
So for the (unphysical) quantum mechanical H+ molecular ion to have true solution, its wavefunction must give the constant conserved total energy E in all space, which means Bohr's realistic model conserving the constant total energy E along some orbit is also possible (= Bohr's H+ molecular ion is also possible, if Schrodinger equation for H+ molecular ion has true solution ).
As I proved Schrödinger equation for helium atoms can never have true solution (= only Bohr's realistic helium atom can have true solution or orbits conserving the constant total energy E ), this quantum mechanical H2+ molecule ion also can Not have true solvable solution conserving the constant total energy E (= in any arbitrary electron's position ) due to this unrealistically-spreading quantum probability wavefunction.
(Fig.2) Kinetic energy = second derivative (= ∇2 ) in Schrödinger equation
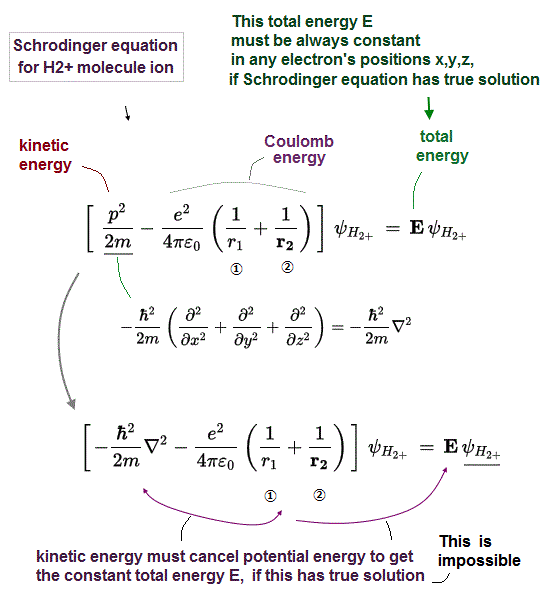
In Schrödinger equation, the constant total energy E is the sum of kinetic energy and Coulomb potential energy.
Schrödinger equation for H2+ molecule ion includes two Coulomb electric potential energy terms, r1 is the distance between an electron and nucleus 1, and r2 is the distance between an electron and nucleus 2 (+ Coulomb repulsive energy between two fixed H2+ nuclei should be also included in Coulomb energy term, but we omit it for simplicity here, because this internuclear Coulomb energy is always the fixed value irrelevant to the electron's position ).
Kinetic energy term is expressed by the second derivative (= ∇2 ), according to de Broglie wave theory.
In order to give the constant conserved total energy E, these two changeable Coulomb potential energy terms must be canceled by other changeable kinetic energy terms (= derivative ) in any electron's position.
↑ But we prove this constant conserved total energy E is impossible in Schrödinger equation for H2+ molecule ion, which means quantum mechanical Schrödinger equation for H2+ molecule ion can never have exact solution (= under the constant total energy E ), hence, quantum mechanics is wrong.
(Fig.3) Kinetic energy operator differentiating wavefunction must cancel Coulomb potential energy term and give the constant conserved total energy E, which is impossible in quantum wavefunction.
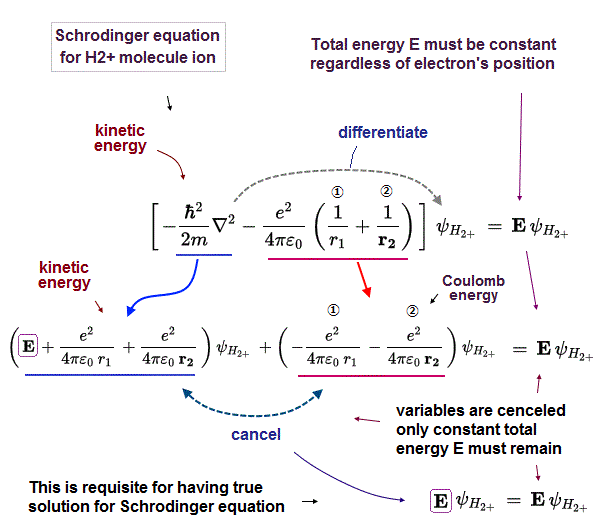
Of course, the total energy E in the ground state of H2+ molecule ion must be conserved and constant in arbitrary electron's position to solve Schrödinger equation for H2+ molecule ion.
So the variable Coulomb potential energy terms (= changeable in different electron's position ) must be cancelled out by their corresponding kinetic energy terms (= kinetic energies are also variable and changing in different electron's positions ) to give the constant total energy E, which is impossible in quantum mechanical wavefunction (= quantum mechanics cannot solve Schrödinger equation for H2+ molecule ion ).
Kinetic energy operator expressed as derivative acts on the wavefunction to give different kinetic energy values in different electron's places.
(Fig.4) Total energy E must be constant and conserved in any places. → Unrealistically two separate independent hydrogen atoms are needed in quantum mechanical wavefunction.
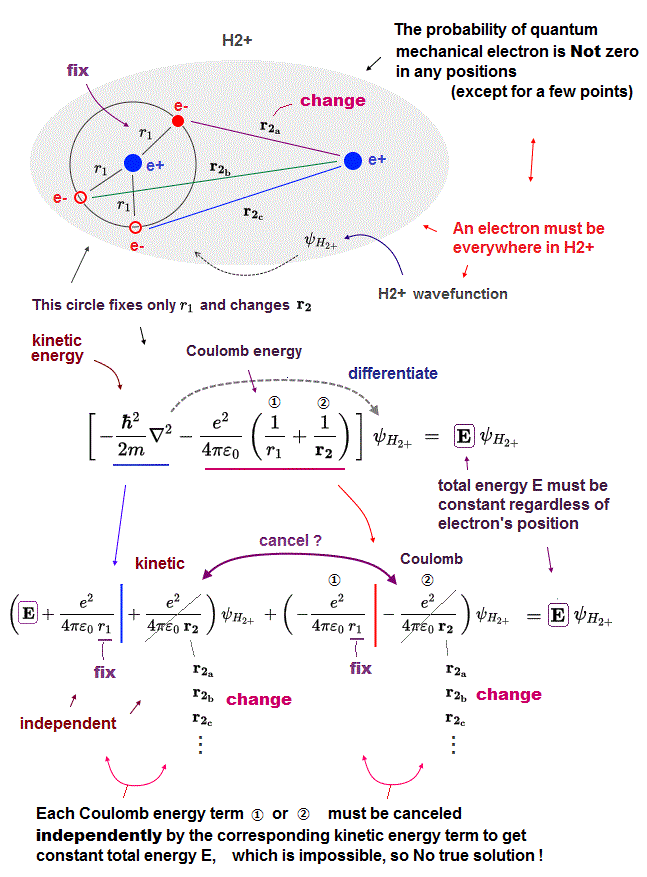
Electron's wavefunction in Schrödinger equation must be always continuous and spreading in all space (= if quantum probability wavefuntion is discontinuous or localized only in one place, the electron's kinetic energy expressed as derivative of wavefunction becomes unrealistically infinite, and cannot give the finite constant conserved total energy E ), which means a quantum mechanical electron must always spread all over the place in H2+ molecule ion.
So we can think about the case or an electron's positions where we fix the valiable r1 (= distance between an electron and nucleus 1 ), changing only r2 (= distance between an electron and nucleus 2 ).
In this case or electron's positions (= when an electron exists on the circular line separated from the left H atomic nucleus by the fixed distance r1, separated from the right H atomic nucleus by the changing distance r2 as shown in the upper figure ), only the second Coulomb energy term (= ② ) including the variable r2 changes, so the corresponding kinetic energy term must cancel only this the second changing Coulomb potential energy term, and the sum of them must give the constant total energy E.
In the same way, we can think about the case or positions where an electron exists on the circular line separated from the right H atomic nucleus by the fixed distance of r2, separated from the left H atomic nucleus by the changing distance r1, which means one variable r2 is fixed, and only the other variable r1 is changed.
↑ In both electron's positions, the total energy E must be always constant and conserved by the corresponding kinetic energy term canceling one variable Coloumb potential energy term independently.
It means each Coulomb potential term (= ①, ② ) must be canceled by the kinetic energy term, independently from each other, which means quantum mechanical H2+ molecular (illusory exact) solution must consist of two independent hydrogen atomic wavefunctions existing around two nuclei
↑ If the exact H2+ molecular ion's exact solution must consist of two independent H atomic wavefunctions, it disagrees with the experimental H2+ molecular ion's energy.
The expermental value of H2+ molecule ion bond energy is -2.79 eV at the bond length (= distance between two H atoms in H2+ ) of 1.06 Å ( this p.5-lower )
When the H2+ molecular ion's exact solution consists of two H atomic wavefunctions, its bond energy becomes 2 × -13.6 eV (= H atomic energy × two independent H atomic energies ) + 13.6×2×0.53/1.06 (= Coulomb repulsive energy between two H atomic nuclei ) + the original hydrogen atomic energy 13.6 eV = 0.0 eV, which cannot give the actual H2+ bond energy of -2.79 eV !
↑ Here we use the hydrogen atomic ground state (= lowest ) energy of -13.6 eV at the average (= Bohr ) radius of 0.53 Å
So this Schrödinger equation can never give the right H2+ moleule ion model due to its unrealistically-spreading continuous probability wavefunction.
(Fig.5) When the distance (= R ) between two nuclei is ∞, the Schrödinger's H2+ molecular (illusory exact) wavefunction gives the lowest energy = No H2 molecular ion's bond is formed, if quantum mechanical H2+ molecular ion has the exact solution !
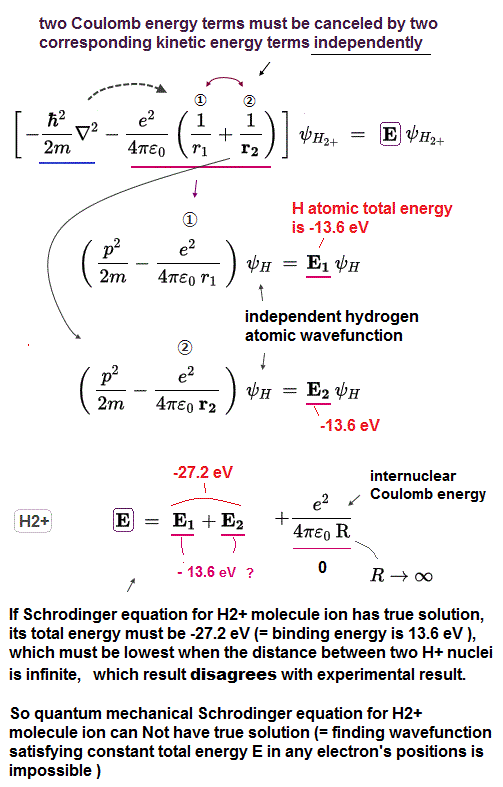
If two Coulomb terms in Schrödinger's H2+ are independent from each other, we can separate the total energy E into two independent H atomic energies (= E1, E2 ).
Each Coulomb energy term is the same as one-electron hydrogen atom, which gives -13.6 eV as the ground state energy.
And we have to add the repulsive Coulomb energy term between two nuclei, which becomes the lowest zero, when the distance is infinite ( R → 0 ). ← The lowest total energy must become the ground state energy, which means the internuclear distance of (unrealistically-solvable) H2+ molecular ion in quantum mechanics must be infinite.
↑ It means No molecular bond, because when internuclear distance is infinite, this quantum mechanical H2+ molecule ion (= if H2+ ion Schrodinger equation has solvable solution ) gives the lowest total energy of -13.6 × 2 eV with biggest binding energy of 13.6 eV.
So, if there is an exact Schrödinger's solution for H2+, the distance between two nuclei must be infinite (= which wrongly gives the lowest ground state energy of the illusory quantum mechanical H2+ ion with bond energy 13.6 eV = far bigger than the actual 2.79 eV ), which is inconsistent with the true H2+ molecule ion !
This is the reason why Schrödinger equation is wrong except the only solvable one-electron H atom.
(Fig.6) No forms of H2+ wavefunctions can be true solution to get constant total energy E.
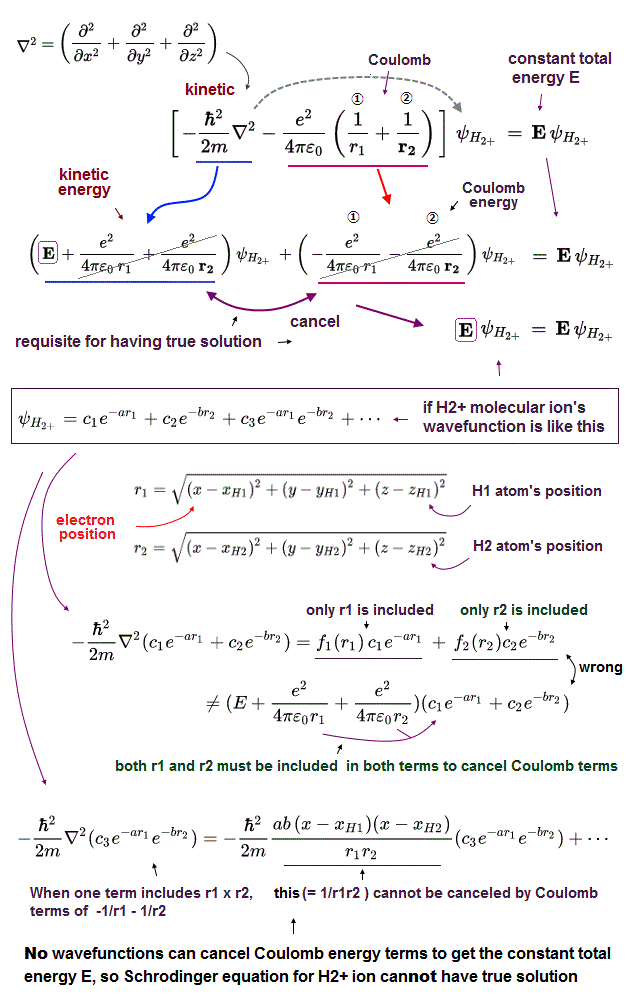
If Schrödinger equation for H2+ molecule ion is solvable or has true solution (= true wavefunction ), kinetic energy term (= derivative ) must cancel two Coulomb energy terms to get the constant (= consreved ) total energy E, which is impossible ( this p.2,p.5-left-last~p.5-right used approximate numerical cut-off or empirical parameters without solving it ).
As shown in the upper figure, No matter what forms of H2+ wavefunctions are prepared, they can Not cancel two Coulomb energy potential terms (= -1/r1 - 1/r2 ).
When the H2+ wavefunction is expressed as the sum of e-r1 + e-r2, the derivative (= kinetic energy ) of this wavefunction is divided into the term containing only r1 variable and the term containing only r2 variable, which cannot cancel two Coulomb energy terms.
When H2+ wavefunction includes the term containing both r1 and r2 like e-r1 × e-r2, the derivative (= kinetic energy ) of this term always gives the term mixing r1 and r2 variables (= r1r2 ), which cannot be canceled by Coulomb energy term (= -1/r1 - 1/r2 ), either.
As a result, it is impossible to solve Schrödinger equation for H2+ molecule ion or have true solution that can give the constant (= conserved ) total energy E in any electron's position.
So quantum mechanics is false.
(Fig.7) So the distance r1 and r2 are NOT independent.
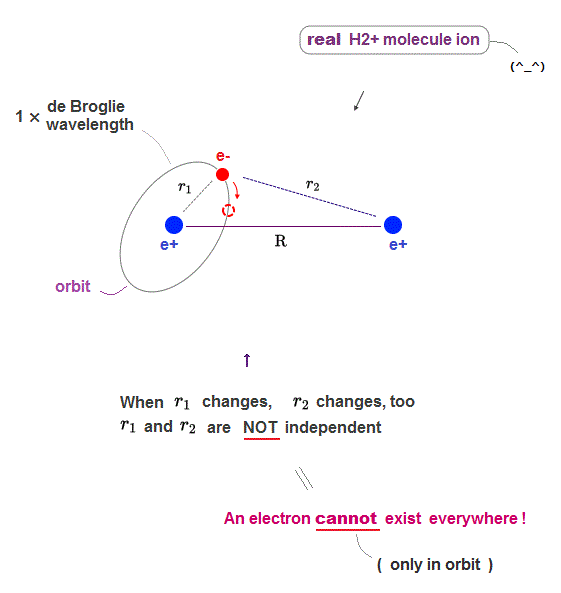
To give the correct H2+ molecule ion model and energy, an electron must be "confined" to some "orbit" instead of quantum mechanical unrealistically-spreading waverunction.
While an electron is moving in the "limited" orbit, the distances r1 and r2 are NOT independent from each other (= r2 is a function of r1 ).
All atomic and molecular orbits are governed by two important factors of Coulomb electric force and de Broglie wave.
Exept for a few special case such as a hydrogen atom and helium atom (= one nucleus ), considering only Coulomb force cannot give the closed orbit, so we must consider the pressure from de Broglie wave (constructive and destructive) interference (= this de Broglie wave influence must be determined in actual experiments as well as the realistic Pauli repulsion ) to obtain the true realistic H2+ molecule ion's closed orbit.

2022/10/22 updated. Feel free to link to this site.