Top page ( correct Bohr model ).
New Bohr model, Neon, Argon.
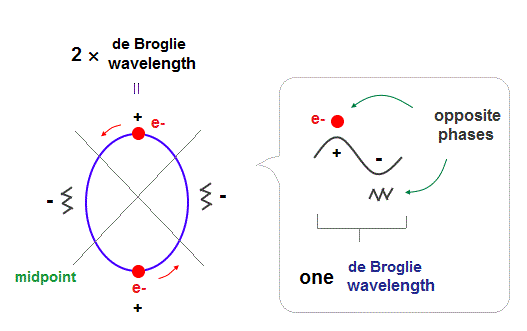
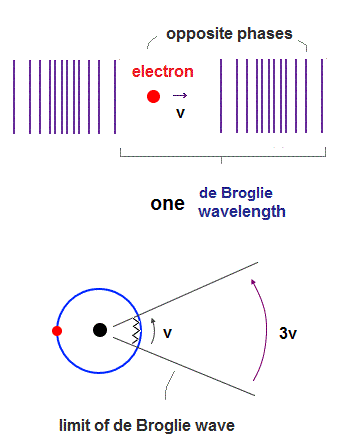
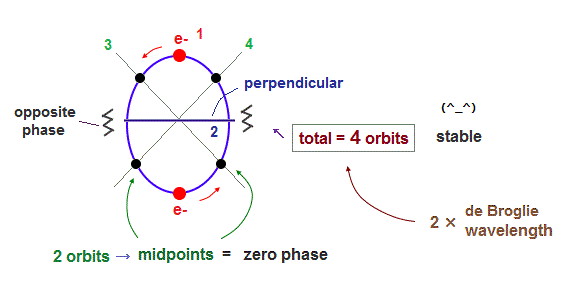
(Fig.1) 2 × de Broglie wavelength orbits. Each is a pair of opposite phases.

One wavelength consists of a pair of "crest" (= + ) and "trough" (= - ) irrespective of transverse and longitudinal waves.
Here we suppose "+" phase contains an electron itself, and "-" phase is compressed by the electron's movement, --- which is " de Broglie wave ".
2 × de Broglie wavelength orbit contains two pairs of ±opposite phases and two midpoint lines.
(Fig.2) de Broglie "longitudinal" wave.
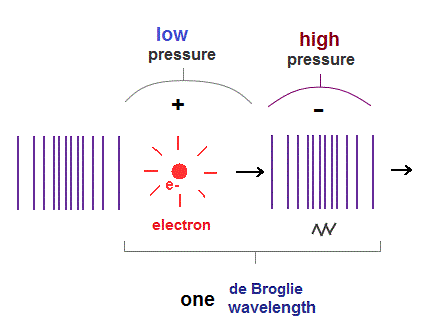
If we consider de Broglie wave as one of "longitudinal" waves, one de Broglie wavelength consists of a pair of "low" (= "+" phase ) and "high" (= "-" phase ) pressure regions.
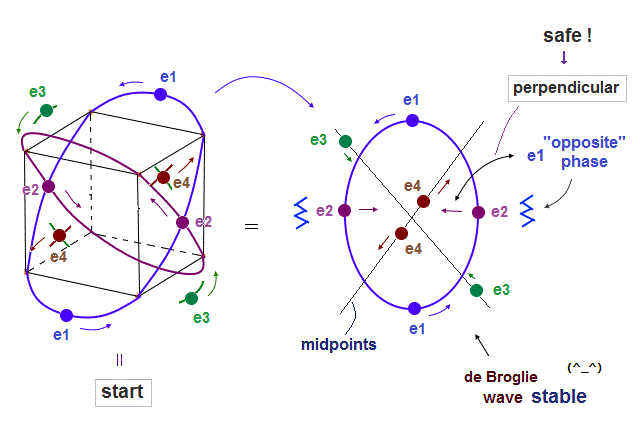
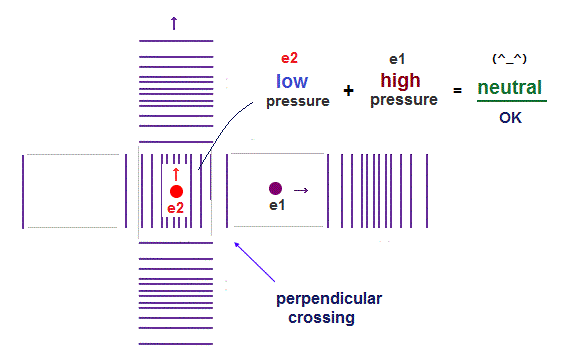
(Fig.3) "Opposite" wave phases interfere with each other, destructively. → "perpendicular".
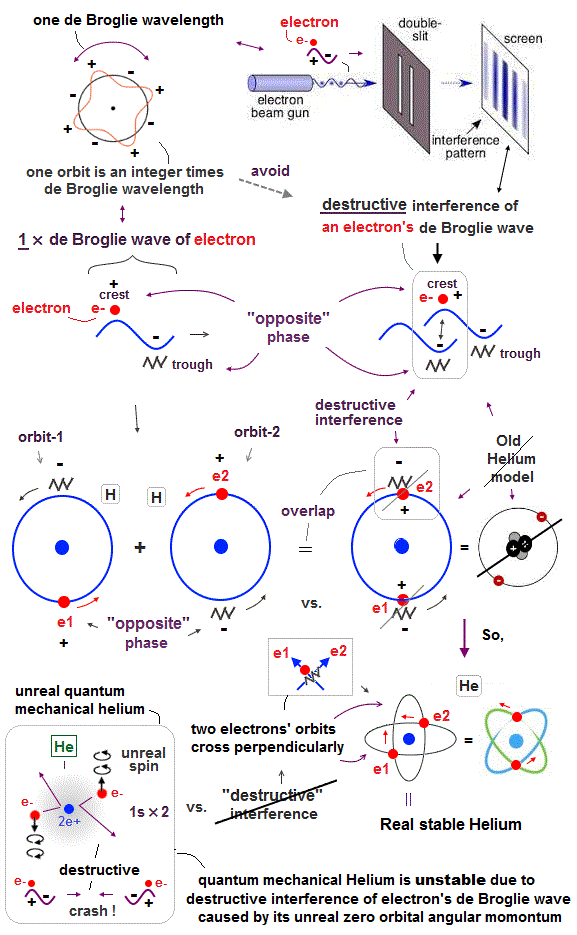
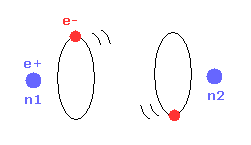
Helium atoms contains two 1 × de Broglie wavelength orbits ( n = 1 ).
So, two opposite wave phases cause "destructive" interference and instability.
To avoid this destructive interference, two orbits of helium have to cross each other "perpendicularly", because "perpendicular" means each wave phase can be independent from another.
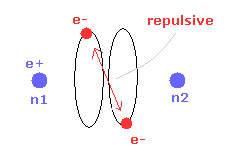
(Fig.4) Two electrons have to pass each other on "midpoint" lines.
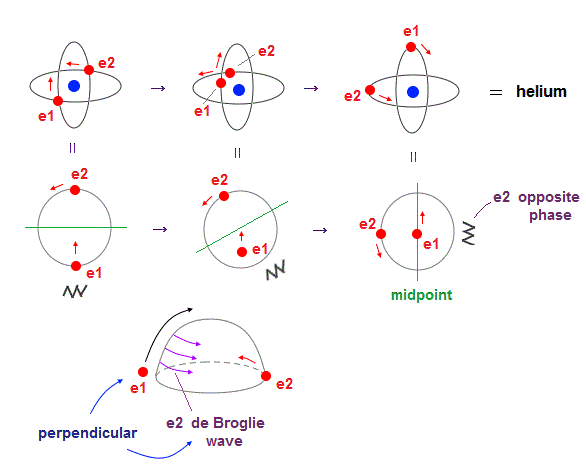
In one de Broglie wavelength orbit, a half of it is "opposite" wave phase.
So, "e1" electron of Fig.4 must go in the direction perpendicular to "e2" orbit to midpoint.
Two electrons in "perpendicular" orbits have to pass each other in the "parallel" direction at "midpoint", because "midpoint" line is zero phase, which has NO influence on another wave.
(Fig.5) Midpoint between ±opposite phases has NO influence on another wave.
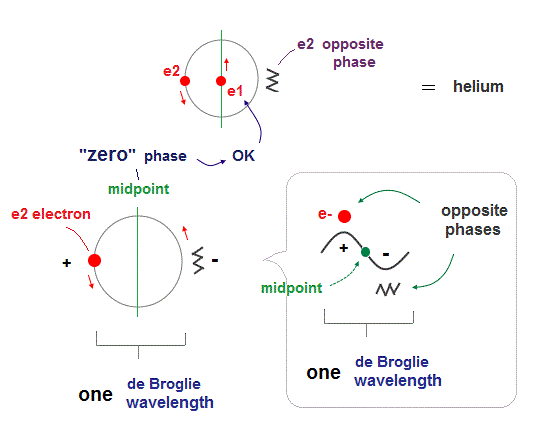
"Midpoint" line between ±opposite phases contains "medium (= neutralized )" zero phase.
So this midpoint has NO influence on another wave phase (= NOT disturb other de Broglie waves ).
So, de Broglie wave can pass each other in the parallel direction, NOT disturbed on the midpoint lines.
(Fig.6) 2 × de Broglie wavelength orbit can naturally contain "two" electrons.
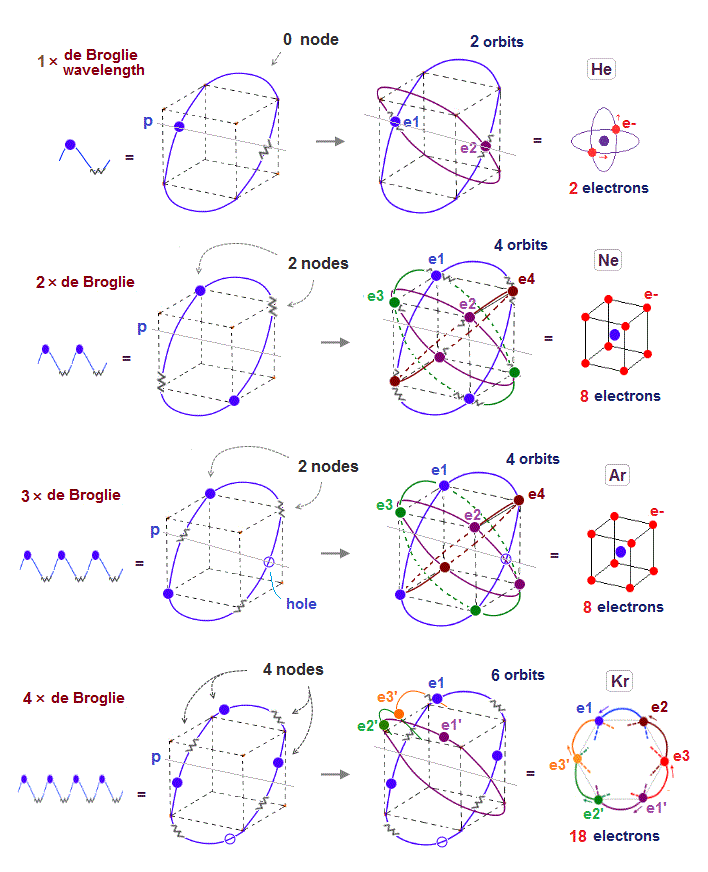
Different from one de Broglie wavelength orbits of helium, two de Broglie wavelength orbit can contain two electrons just on the opposite sides of the nucleus.
Because the wave phases at the opposite positions are the same (= both "+" phase ).
So two electrons can naturally enter the same orbit, NOT expelled by destructive interference.
(Fig.7) 2 perpendicular orbits + 2 midpoint lines = 4 orbits in Neon.
We can explain new Neon model using 4 orbits, each contains two electrons ( 2 × 4 = 8 valence electrons ). Each two orbits form a pair, when they cross perpendicularly.
When "two orbits" cross perpendicularly in each pair, each de Broglie wave pair must NOT be disturbed and obstructed by another pair of waves.
"NOT disturbed" means each pair ( consisting of two orbits ) must be on the midpoint lines of orbits in another pair. As a result, Neon can contain the maximum 4 orbits stably.
(Fig.8) Orbits of Neon cross each other "perpendicularly".
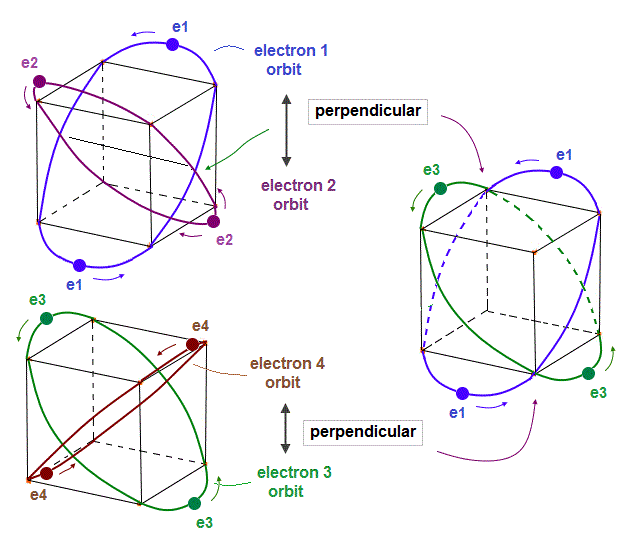
(Fig.8') Orbits of Neon cross each other "perpendicularly".
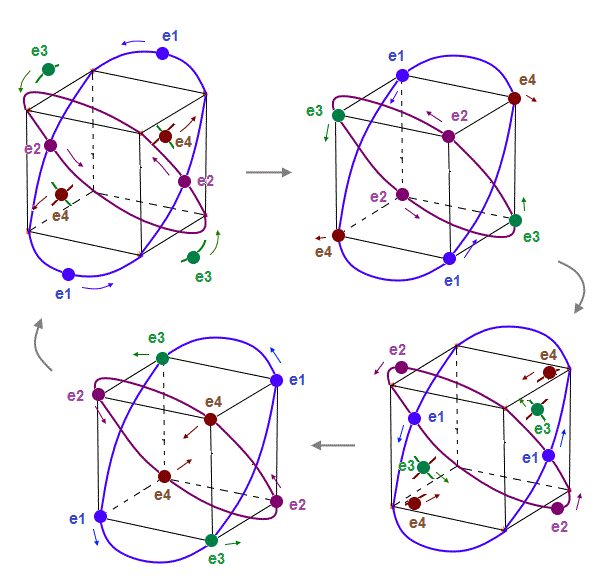
As shown on this page, we can show the appropriate new Neon model, in which orbits can cross each other "perpendicularly". "Perpendicular" crossing means they can avoid "destructive" interference.
(Fig.9) Orbits (= opposite wave phases ) always cross each other "perpendicularly".
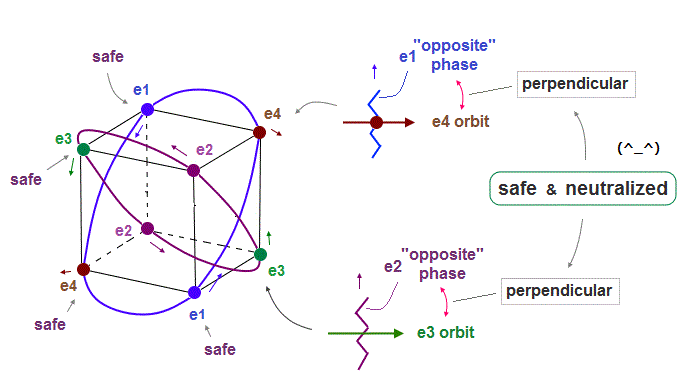
Each electron can cross other electrons' orbits perpendicularly, when they are opposite wave phases to each other, because "perpendicular" crossing avoids destructive interference.
Furthermore. crossing of "opposite" wave phases can neutralize total wave phases at all points ( ±phases = zero ).
"Neutralization" of wave phases means any other electrons can be free from other wave ( bad ) influences, and move stably and independently, NOT to be disturbed.
(Fig.10) de Broglie "longitudinal" wave.
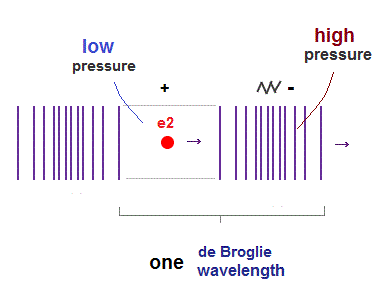
If we consider de Broglie wave as some longitudinal wave, each de Broglie wavelength consists of a pair of "low" and "high" pressure.
(Fig.11) "Low" + "low" pressures form "very low" pressure. - unbalanced.
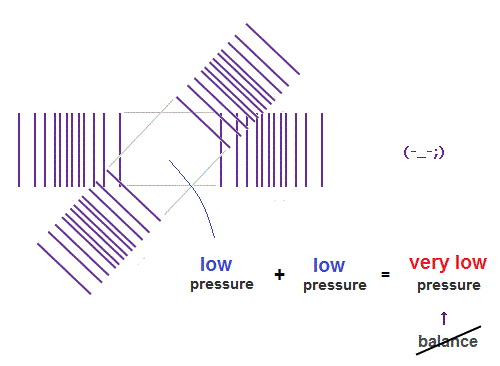
When "low" and "low" pressure parts cross each other, it generates "very low" pressure.
"Very low" pressure in de Broglie wave field is bad for the pressure balance.
(Fig.12) "High" + "high" pressures form "very high" pressure.
When "high" and "high" pressure parts cross each other, it generates "very high" pressure.
"Very high" pressure in de Broglie wave field is bad for the pressure balance, too.
Of course, when both phases and their directons (= parallel ) agree with each other, it causes "constructive" interference, so enhances their displacement "synergistically".
But two de Broglie waves cross each other "perpendicularly", they are independent from each other. In this case, "field pressure" is very important factor to determine each orbit.
(Fig.13) "Low" and "high" pressure waves cross "perpendicularly" ← stable !
When "low" (= "+" phase ) and "high" (= "-" phase ) of de Broglie waves cross "perpendicularly", it generates "neutral" pressure in field. "Neutral" pressure is the most stable in balance.
Furthermore, "perpendicular crossing" can keep each electron's de Broglie wave phase independently.
(Fig.14) Opposite "e2" and "e1" phases form midpoint phase at e4,e3 crossing point.
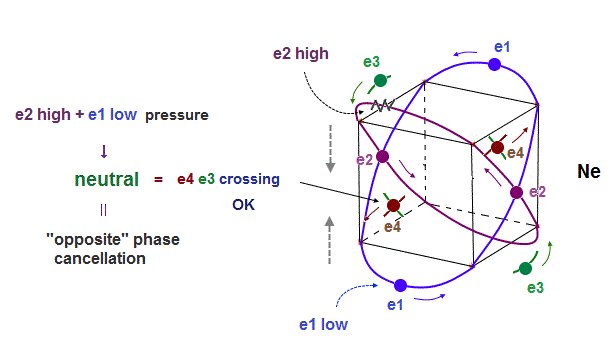
In new Neon model, when two orbits cross perpendicularly, they are NOT disturbed by other orbits.
In Fig.14, "e4" electron cross "e3" opposite phase wave perpendicularly.
At this crossing point ( of "e3" and "e4" ), the influences from other electrons (= e1, e2 ) must be cancelled out and zero (= midpoint ) to keep the crossing waves stable.
As you see Fig.14, from the viewpoint of e3,e4 intersection, "e2" (= upper ) and "e1" (= lower ) orbits are just symmetrical and "opposite" wave phases !
This is the reason why the 4 even-number orbits of Neon can be stable.
When 2 orbits cross perpendicularly, other 2 symmetrical orbits cancel each other at another intersection.
(Fig.15) H2 molecule. two "perpendicular" orbits.
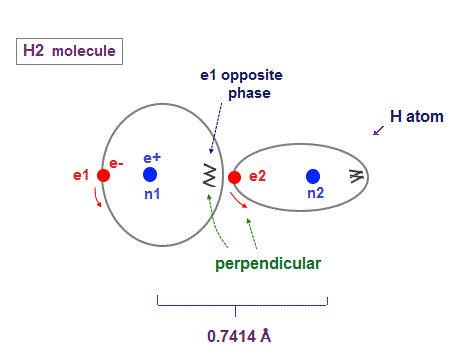
Hydrogen molecule (= H2 ) contains two hydrogen atomic orbits with 1 × de Broglie wavelength.
Condidering Coulomb interaction, when one electron (= e2 ) approaches another nucleus (= n1 ), these two orbits must cross "perpendicularly" to avoid destructive interference.
Two orbital de Broglie waves in the opposite direction cancel each other at a distance, so magnetic field loop is disrupted and its magnetic moment created in H2 is almost zero.
(Fig.16) Two orbits are too close → repulsion between electrons become stronger.
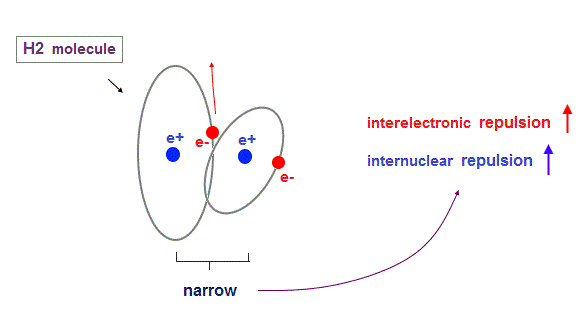
When internuclear distance of H2 molecule is shorter than the experimental value (= 0.7414 Å ), each electron is more attracted to another nucleus.
So electrons tend to stay longer between two nuclei.
Furthermore, the repulsive Coulomb force between two closer nuclei becomes stronger.
These increasing repulsive Coulomb forces between electrons and nuclei prevent two H2 nuclei from approaching each other.
(Fig.17) Most stable H2 configuration.
On this page, we can explain the experimental internuclear distance of H2 by Virial theorem.
"Average" positions of each hydrogen orbit is as shown in Fig.17.
As the two nuclei come closer to each other, each electron can interact with two positive nuclei.
So, the bond energy becomes bigger, which means stable H2 molecule is formed.
(Fig.18) Repulsive force of two electrons.
But when the two nuclei come closer to each other than the experimental value of 0.7414 Å, the repulsive force between two electrons are stronger.
Each hydrogen orbit must keep 1 × de Broglie wavelength, which prevents the orbit from being smaller. Stronger repulsion between two electrons reduces "effective" central positive charge of each hydrogen.
So under the common de Broglie wave's condition (= 1 × de Broglie wavelength ), each hydrogen radius "r" is larger, and bond energy is smaller than the experimental value in Fig.18.
(Fig.19) Carbon = 4 valence electrons + 4 holes = "tetrahedral".
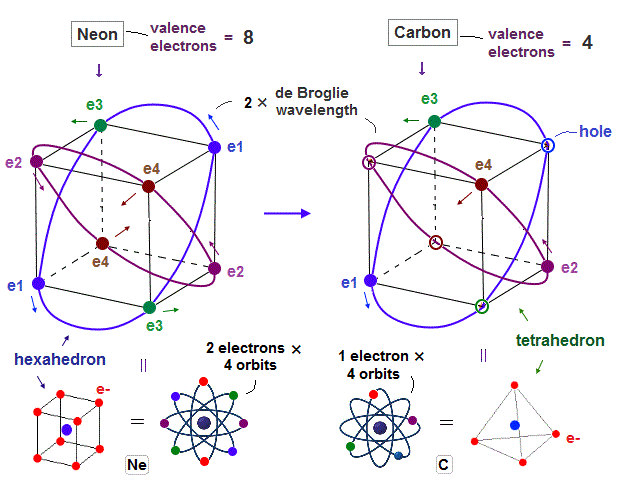
Carbon has four valence electrons ( n = 2 ), so easily forms "tetrahedral" shape due to Coulomb balance. Regular "tetrahedron" is a part of regular "hexahedron".
So Carbon atom can be thought to consist of 4 tetrahedral electrons + 4 holes like Neon.
(Fig.20) Hydrogen ±electron's wave phases synchronize with carbon. →"hexahedron".
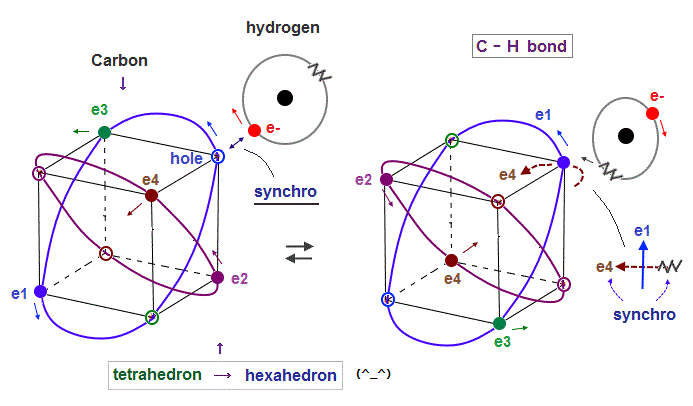
As I said in Fig.6, 2 × de Broglie wavelength orbit can contain two electrons.
Carbon tetrahedral-shape orbit includes four electrons and four holes.
When electrons of hydrogen atom approach and synchronize with the same phase hole, they can fuse and form stable hexahedral structure with 8 electrons like Neon.
When opposite (= "-" ) wave phase approaches carbon, hydrogen orbit synchronize with the opposite ( = "-" ) wave phase ( in this case, "e4" wave ), which is perpendicular to e1 orbit.
Because the same phase waves interfere "constructively" and enhance each other, and "opposite" phases repel each other due to their different phase motions.
If we consider field oscillations in three directions (= x, y, z ), hydrogen orbit can oscillate periodically in concert with another same wave phase.
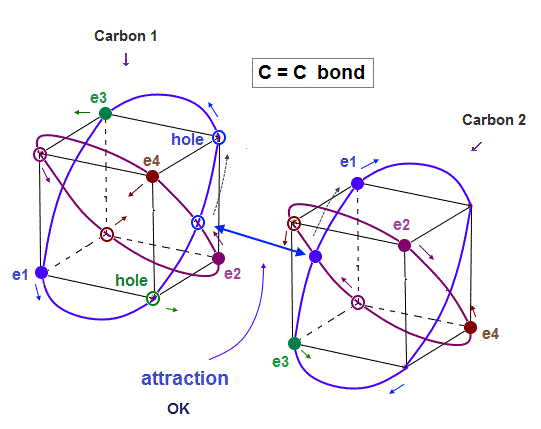
(Fig.21) In C-C bond, an electron synchronize with another hole.
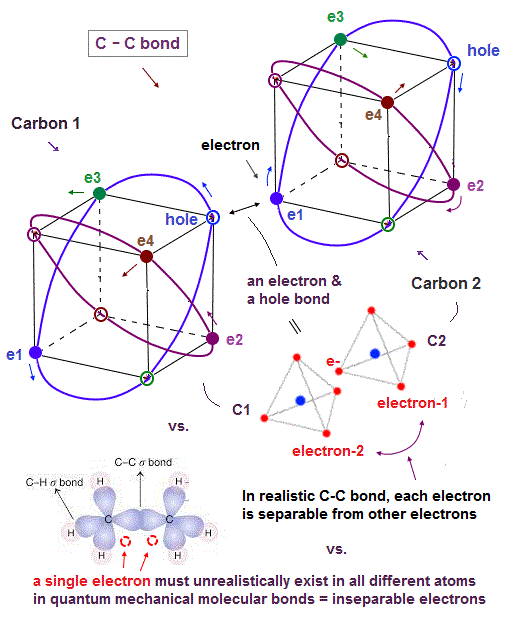
Also in carbon-carbon ( C-C ) bond, electons are thought to aim at stable hexahedral structure like Neon by electron-hole pairs.
As shown in Fig.21, an electron of one carbon can always approach a hole of another carbon, which is stable in Coulomb energy.
Unlike the unrealistic quantum mechanical molecular bonds where every single electron must always exist in all different atoms simultaneously for generating the unphysical exchange energy lacking exchange force, this realistic C-C molecular bond has the actually-separable and movable electrons that can be put to practical use.
As shown on this page, the average carbon radius is about 0.64 Å, considering its ionization energies and 2 × de Broglie wavelength.
This bond length is almost kept in different carbon-atomic bonds ( C-H, C-C .. )
(Fig.22) In C=C, C=O bonds, two electron-hole pairs are formed.
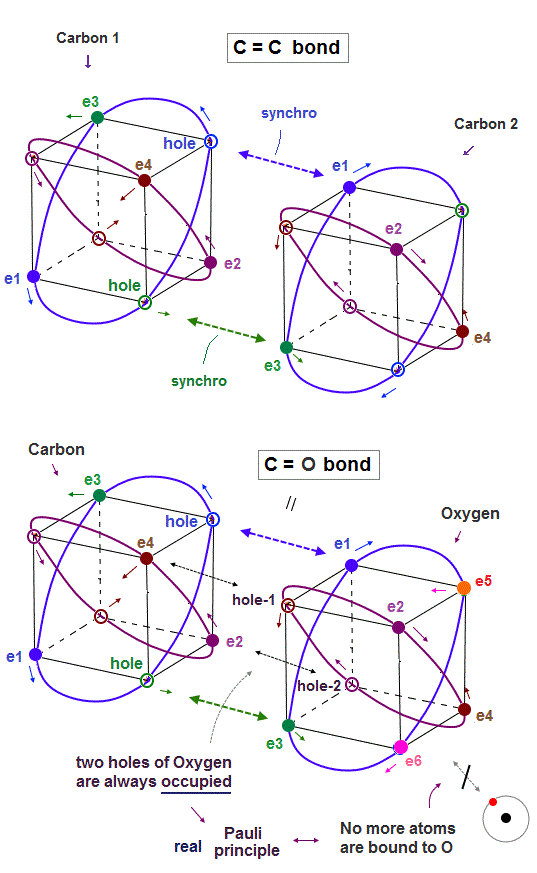
In C=C double bond, two electron-hole pairs are formed between two carbons.
In Fig.22, "e1" and "e3" electrons of carbon 2 approach correspondent holes of carbon 1, and make Neon-like hexahedral structure.
Comparing Fig.21 and Fig.22, you will easily find C=C bond is shorter than C-C bond.
In the same way, C=O double bonds can be explained by this realistic atomic models.
The point is two empty holes of oxygen atom with six valence electrons are always occupied by two electrons from the other carbon atom, as seen in Fig.22 lower.
So No more electrons of other atoms can approach or form new molecular bonds with this oxygen atom of C=O bond, which is the realistic mechanism of Pauli explucion principle.
And this realistic tetrahedral carbon's valence electrons considering Coulomb interaction correctly can perfectly explain why ethylene (= H2C=CH2 ) double bonds become "plane-like" shape.
(Fig.22') Opposite wave phase of the external hydrogen (= H ) atom interferes destructively with more than two electrons of oxygen atom whose holes are already occupied by forming O=O double bond in O2 molecule. = real Pauli repulsion
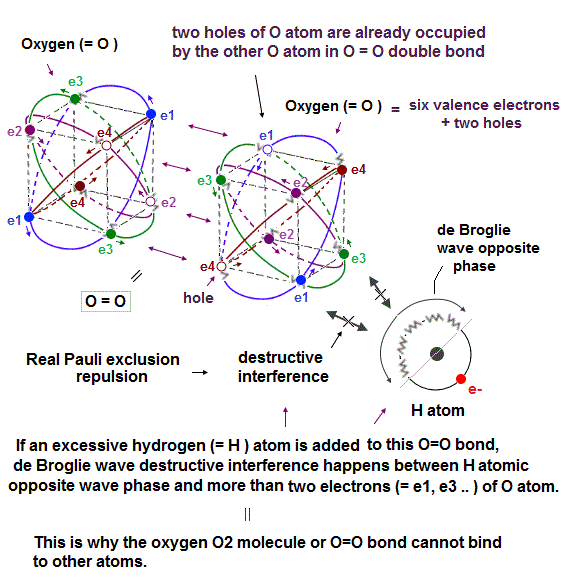
In Oxygen (= O2 ) molecule, two oxygen atoms bind to each other by covalent O=O double bond.
We can explain why this O2 molecule cannot bind to more atoms using real Pauli principle repulsion based on destructive interference of electrons' de Broglie wave that was experimentally verified.
As shown above, two holes of each oxygen atom (= O ), which has six valence electrons and two holes, are already occupied by electrons of the other oxygen atom in this O2 or O=O double bond.
So there are No more vacant holes in this O2 or O=O double bond into which other external electrons get.
Even if another external atom (= ex hydrogen or H atom ) tries to bind to this already-saturated O2 molecule, it causes the destructive interference between this O atomic electrons and the de Broglie wave's opposite phase of this H atom (= jagged part covering the half of H atomic orbit which is 1 × de Broglie wavelength ).
As shown in upper figure, the excessive H atomic electron's orbit cannot merge or synchronize with one of O atomic (vacant) electron orbit, due to the lack of holes (= two holes of O atom are already occupied by the other O atom ) and Coulomb repulsion between these electrons of H and O atoms.
So this external H atomic electron orbit must approach some inappropriate positions (= which positions tend to cause destructive interference between other electrons' orbits ), for example, just between the e1 and e3 electrons of O atom.
If this opposite wave phase of the excessive H atomic electron's de Broglie wave tries to be perpendicular to one electron (= ex. e3 ) of the oxygen atom ( in the middle position between e1 and e3 electrons ), this opposite wave phase cannot be perpendicular to other oxygen's electrons such as e1, e2.. simultaneously, which causes destructive interference of electrons' de Broglie waves.
As a result, electrons are expelled from the orbit, and this molecular bond is unstable and broken, which is why O2 molecule or O=O double bond cannot bind to another external atom. = real Pauli repulsion
This is real Pauli principle repulsion instead of unrealistic quantum mechanical Pauli exchange energy with inseparable electrons.
(Fig.22'') The opposite phase (
= jagged line ) of Hydrogen H atomic electron orbit's de Broglie wave interferes destructively with Neon's e3 electron's orbit. → H-Ne bond is impossible
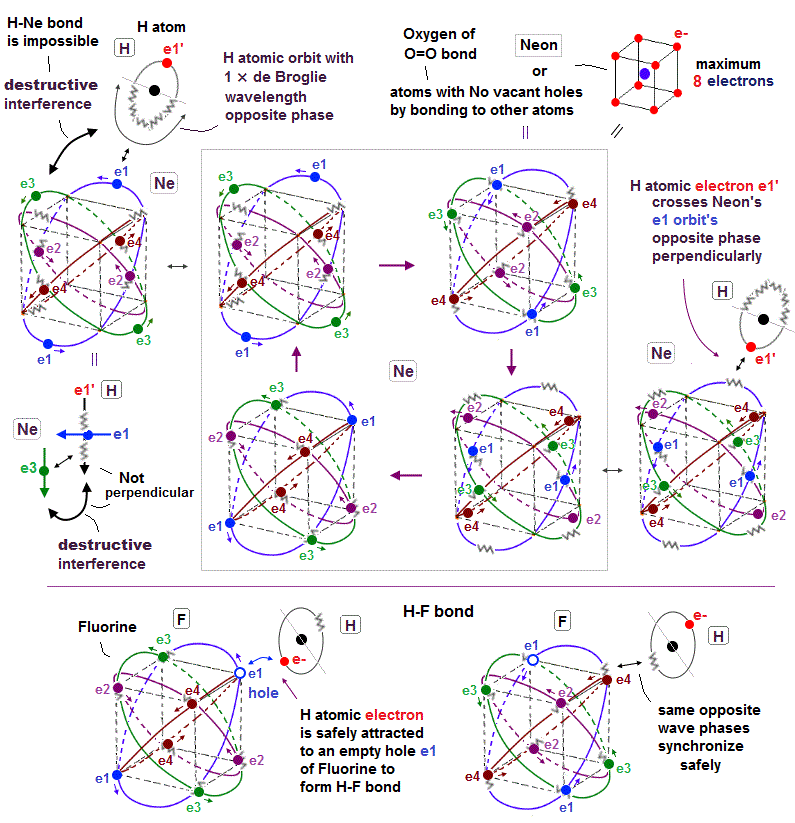
Neon or atoms with No holes by already covalently bonding to other atoms (= such as Oxygen atom of O=O double bond ) cannot form any more covalent bonds with other atoms.
We can explain this Pauli pexclusion principle forbidding no more covalent bonds with saturated atoms using de Broglie wave destructive interference.
In the upper figure, an external hydrogen (= H ) atomic electron crosses the Neon's e1 orbit's opposite phase (= jagged line ) perpendicularly to avoid destructive interference.
↑ Neon already has eight valence electrons and No empty holes, so this external H atomic electron cannot approach the vertices of the hexahedral Neon atom, instead it has to approach the inappopriate position such as the middle of two Neon's vertices.
The point is this H atomic orbit perpendicular to e1 orbit cannot be perpendicular to other orbits such as e3 orbit.
As a result, the H atomic de Broglie wave's opposite phase destructively interferes with Neon's e3 orbit, and makes H-Ne covalent bond impossible.
On the other hand, a fluorine (= F ) atom with seven valence electron and one hole can safely bind to an external H atomic electron, and form H-F covalent bond.
Because the H atomic electron can safely approach and synchronize with the empty hole (= same wave phase ) of F atom without being repelled by other electrons and de Broglie waves.
And the H atomic opposite phase (= jagged line ) also can synchronize with the opposite phase of F atom safely (= two jagged de Broglie waves in the same direction and the same phase of H and F atoms synchronize with each other, and let each other's phase safely return to their original positions or atoms ), which doesn't disturb other electrons or cause the destructive interference.
This is the realistic mechanism of covalent bonds and Pauli repulsion based on real de Broglie wave interference and electron's hole.
In order to avoid crashing into other repulsive electrons between different atoms in molecular bonds, some electrons can jump into holes and create new holes in their original positions that can bind to other atomic electrons safely.
As shown in this figure, the carbon with four valence electrons and four holes (= each 2 × de Broglie wave orbit has one electron and one hole ) can more easily and smoothly provide two empry holes to ther neighboring atoms (= C or O ) in double bonds ( C=C, C=O ) than the oxygen atom (= O ) with six valence electrons and two holes.
It is more difficult for the oxygen atom with six valence electrons and only two holes to prepare two empty holes for the neighboring atoms, because the oxygen's six valence electrons (= instead of holes ) are more likely to approach the neighboring atom blocking holes from approaching the neighboring atom than carbon's four valence electrons.
This is why O=O double bond (= bond energy = 494 kj/mol ) is weaker than C=O double bond (= bond energy = 799 kj/mol ) or C=C double bond (= bond energy = 602 kj/mol ).
↑ In O=O double bond in the oxygen molecule, the six valence elenctrons of each O atom are more likely to clash against the other O atom's six valence electrons than C=O (or C=C ) double bond with more empty holes, hence, O=O exerts stronger Coulomb repulsion among their more abundant valence electrons and weakens O=O bond strength compared to C=O bond.
This is the same reason as why F-F (= fluorine-fluorine ) bond is weaker than Cl-Cl (= chlorine-chlorine ) bond, though F atom has more compact and denser electrons clouds than larger Cl atom with lower-density electron cloud, which means quantum mechanical wavefunction or electron cloud model (= whose molecular bond mechanism is based on electron cloud penetration without moving or avoiding other electrons ) gives the wrong results where the F-F (or O=O ) bond with denser electron cloud becomes stronger than Cl-Cl (or C=O ) bond.
On the other hand, the oxygen atom with more valence electrons can form stronger molecular bond with atoms with a small number of valence electrons such as H atom (= O-H bond is stronger than C-H bond ), because the abundant O atomic valence electrons are more likely to be attracted to H atomic positive nucleus without being repelled by H atomic fewer valence electron.
(Fig.23) "e1" ( and "e2" ) electrons pass "midpoint" between two nuclei.
As two carbon nuclei are closer to each other, their repulsive Coulomb force becomes stronger.
To cancel this nuclear repulsion, each electron must enter between C = C nuclei.
Considering actual orbit of each electron, you find "e1" and "e2" electrons pass the midpoint between two nuclei periodically, which can cancel stronger internuclear repulsion.
(Fig.24) Alternating between "recipient" and "donor" carbons makes "plane".
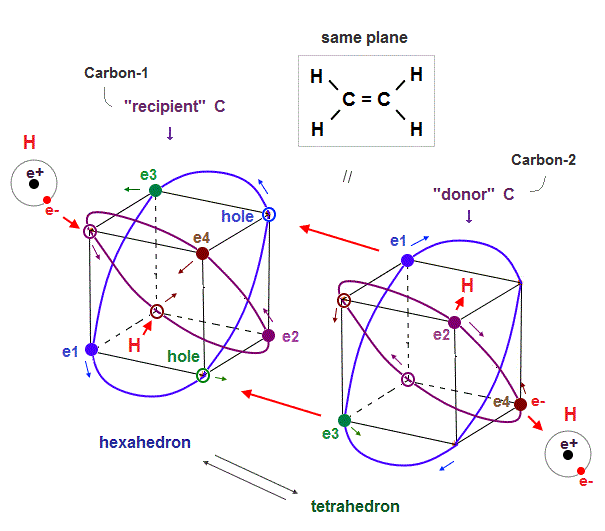
Why does ethene or ethylene (= H2C=CH2, double bonds ) have a "plane-like" structure ?
The point is the positions and motions of electrons of hydrogen (= H ) atoms on the left and right sides decide this plane-like structure.
In the upper Fig.24, the left-side two H atomic electrons approach the carbon-1's two holes or nucleus (= recipient C ), and the right-side two H atomic electrons move away from the carbon-2 (= donor ) by being repelled by the carbon-2's electrons.
So when two left-side ( or right-side ) electrons approach the central carbon-1 ( or carbon-2 ) nucleus, the other two right-side ( or left-side ) electrons need to move away from the central carbon-2 ( or carbon-1 ) atoms.
Because if all four electrons of H atoms approach two central carbon atoms simultaneously, the central two carbons tend to become negatively charged at the same time, and strongly repel each other.
So to keep the balanced electrically-neutral state of two central carbon atoms, when two H atomic electrons approach one carbon atom, the other H atomic electrons should move away from the other carbon atom (= the sum of central two carbon atomic charge becomes balanced and electrically-neutral ).
↑ In this case, four H atoms have to be distributed in the same plane, as shown in the upper Fig.24, considering the tetrahedral distribution of each carbon's four valence electrons at the same time ( a negative electron tends to be attracted to a positive hole ).
In each carbon atom, the carbon's four original valence electrons and external four electrons have to be arranged in the hexahedral way (= the symmetrical eight electrons need to fill the valence shell as shown in octet rule ) to keep Coulomb electrically symmetry (= if this hexahedral symmetrical arrangement is broken, the carbon's asymmetrical 2 × de Broglie wavelength orbits tend to cause destructive interference ).
And at the same time, the internal Coulomb repulsion inside the entire ethylene has to be as small as possible.
↑ These two requirements make the ethylene plane-like shaped as observed.
This is a realistic reason why ethene has the plane-like distribution.
(Fig.25) ↓ Ethane (= C-C bond) and ethyne (= triple bonds )
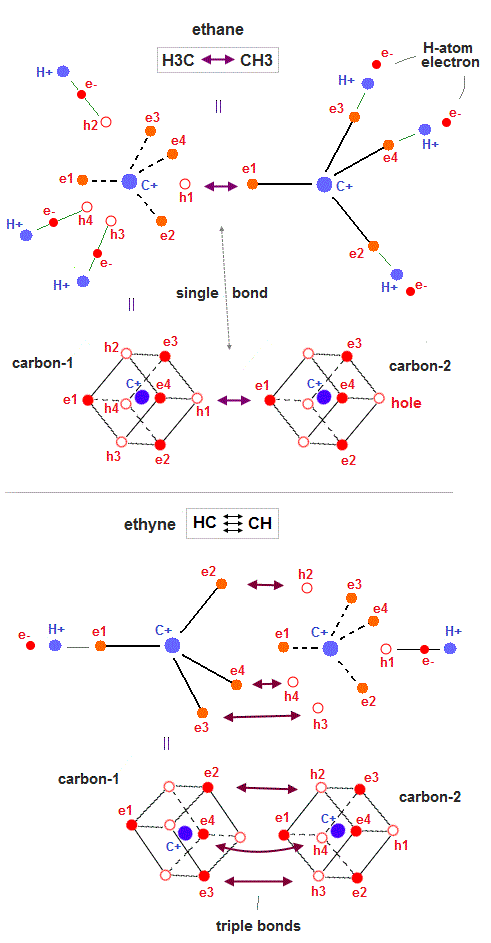
All molecular bonds such as ethane (= H3C-CH3 = C-C single bond ) and ethyne (= or acetylene, HCCH, triple bonds ) can be also explained by realistic moving electron models.
In Fig.25 upper, three hydrogen H atomic electrons approach three holes of the carbon atom-1 (= each carbon has four 2 × de Broglie wavelength orbits with one electron and one hole ), and one valence electron of the carbon atom-2 approaches the remaining hole of the carbon-1 to produce the balanced regular hexahedral distribution of 8 electrons around the carbon-1.
This is a realistic model of ethane H3C-CH3 molecular bond.
Electrons are moving between holes of the carbon-1 and carbon-2 (= or H atom and carbon atoms ) back and forth, alternately, because electrons with kinetic energies are actually moving.
As shown in Fig.25-upper, when two electrons of two left-lower hydrogen atoms approach two holes (= h3, h4 ) of the left carbon atom, the entire carbons' electron are pushed in the opposite (= right-upper ) direction (= with respect to the C-C center ), repelled by these left-side hydrogen atomic electrons.
↑ So three hydrogen atoms on the right side need to be arranged just on the opposite sides (= with respect to the center point of C-C ) from the left-side hydrogen atoms, and attract the electrons pushed by the left-side hydrogens' approaching electrons by exposing their positive nuclei (= when the left-side hydrogens' electrons approach the left carbon, the right-side hydrogens' electrons move away from the right carbon exposing their nuclei just on the opposite sides of the C-C center to reduce internal Coulomb repulsion ).
In Fig.25 lower, three electrons (= e2,e3,e4 ) approach three holes of the carbon-2 and form triple CC bonds of ethyne or acetylene (= HCCH ).
These are realistic single, double, triple molecular bonds based on actually moving electrons instead of unscientific quantum mechanical electron clouds or wavefunctions.
(Fig.26) ↓ Carbon (= C ) can pull oxygen (= O ) electrons in CO ?
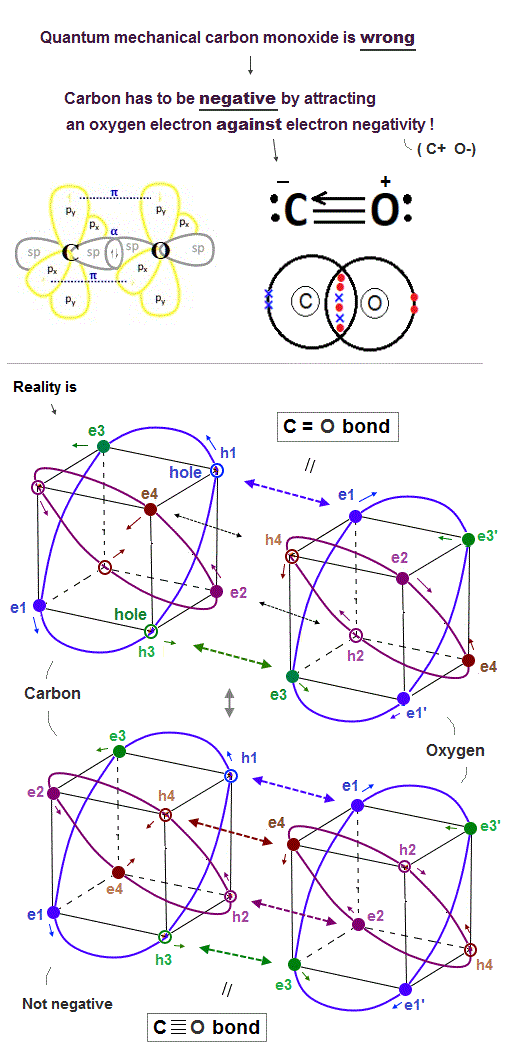
In fact, quantum mechanical molecular orbital theory cannot explain the carbon monoxide (= CO ), hence wrong.
A carbon atom (= C ) has four valence electrons, so C atom has to pull four additional electrons from the other oxygen atom to fill its n = 2 orbitals with the maximum 8 valence electrons (= octet rule ) and become the balanced regular hexahedral neon-like distribution.
On the other hand, an oxygen atoms (= O ) have six valence electrons, hence, the O atom needs to pull two additional electrons from the other C atom to fill its outer orbitals with the maximum 8 valence electrons to meet the octet rule.
To satisfy this stable CO molecular bond condition, quantum mechanics has to make an unrealistic demand that a carbon atom should pull and steal the oxygen's two electrons and become negative ion (= C- O+, this last ), and form triple covalent bonds (= one σ bond + two π bonds ).
↑ This quantum mechanical explanation is contradictory and impossible, so quantum mechanics is false.
Because the electronegativity (= power to pull electrons ) of the oxygen atom is stronger than the carbon atom, hence, a carbon atom cannot be an unreal negative ion by pulling and attracting the oxygen's electron, instead, the carbon tends to lose its electron and become positive ! ← Quantum mechanical carbon monoxide against electronegativity (= C- O+ this p.20 ) is contradictory and false.
As shown in Fig.26-lower, we can explain the carbon monoxide (= CO ) in more realistic way using realistic moving electrons without relying on the unrealistic carbon negative ion of quantum mechanics.
Unlike the unscientific static quantum mechanical wavefunctions or electron cloud, realistic electrons are constantly moving.
So the realistic CO molecular bond is constantly changing between two states of two electrons of the carbon approaching two holes of the oxygen (= filling oxygen's outer orbital with the maximum 8 electrons = balanced state-1 ) and four electrons of the oxygen approaching the carbon's four holes (= filling the carbon's outer orbital with the maximum 8 valence electrons = balanced state-2 ) without unrealistic ionization.
A carbon atom of CO molecule doesn't bind to any other atoms than a single oxygen atom, so four valence electrons of the carbon can move to the opposite side (= left-side in Fig.26-lower ) of the oxygen atom at the same time transiently so that four oxygen electrons can approach the carbon nucleus transiently.
↑ Realistic carbon atom does Not need to be the unrealistic negative ion claimed by quantum mechanics, instead, electrons of oxygen and carbon are constantly moving and approaching each other's nucleus alternately.
This is the realistic model of carbon monoxide with No contradictions.
(Fig.27) Quantum mechanics requires only two electrons of the central O atom to unfairly move around the other lateral O atoms as a constant unreal ion. ← impossible
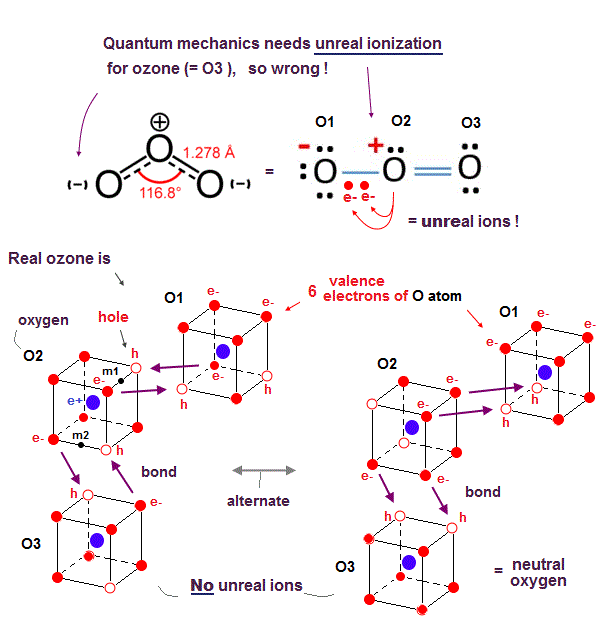
Also in ozone (= O3 ) molecule consisting of three oxygen atoms (= O ), quantum mechanics needs the unreally constant ionization inside the ozone, so quantum mechanics is wrong.
As shown in the upper figure of Fig.27, the right-side oxygen atom (= O3 ) and the central oxygen atom (= O2 ) can satisfy the quantum mechanical octet rule by sharing two additional electrons with each other (= O2=O3 ) filling both their valence shells with eight electrons like stable noble gas, forming the ordinary oxygen molecular double bond ( O=O ).
So the central O2 atom needs No more additional electrons after sharing two additional electrons with the right-side O3 atom.
But the remaining left-side O1 atom still needs two additional electrons to satisfy the octet rule (= filling the outer shell with eight electrons ).
It means only two electrons of the central electrons need to be unfairly delocalized and spread over both the left-side O1 and O2 atoms simultaneously and constantly, which requires the unreal constant ionized state (= the left-side O1 atom must become a constantly-negative ion or O-, and the center O2 atom must become a constantly-positive ion or O+ ) inside O3 molecule to satisfy the octet rule.
↑ Thinking commonsensically, this unreal ionization required by the unscientific quantum mechanical molecules is physically impossible.
Because the ionization energy of the oxygen atom (= 13.61 eV ) is much bigger than the O=O molecular bond (= only 4.98 eV ). ← There is No energy enough to cause such an unrealistic ionization (= O- O+ ) required by the outrageous quantum mechanical molecular bonds ! ← Quantum mechanics is false.
In the quantum mechanical static wavefunction or electron cloud always spreading all over the space, two electrons of the central O2 atom must spread all over both O1 and O2 atoms simultaneously (= which means the unreal ionization of O- O+ ) to cause this unreal molecular bond based on exchange energies.
Quantum mechanical molecular orbital (= MO ) theory requiring each single electron to exist in two different atomic wavefunctions simultaneously ( this p.7 ) always suffers the unreal ionized or delocalized states even in the ordinary neutral molecular bonds ( this p.5-upper ).
In the realistic atomic or ozone model based on actually-moving electrons as shown in Fig.27-lower, each oxygen atom has six electrons and two holes (= in four 2 × de Broglie wavelength orbits ) where two electrons of each oxygen can fill two holes of each other's oxygen constantly and alternately just by moving and approaching other oxygens' nuclei without the quantum mechanical unreal ionization.
Because the realistic actually-moving electrons can exert strong Coulomb attraction when electrons are just passing between different atoms without causing the unreal ionization.
Each bond length (= 1.28 Å ) of the ozone is slightly longer (= weaker ) than the O=O bond length (= 1.21 Å ) of the ordinarly oxygen molecule, because the central oxygen atom of the ozone needs to direct its two holes toward both left and right-side oxygen atomic electrons, which generates more Coulomb repulsion between three oxygens' electrons than the ordinary oxygen molecule consisting of two oxygen atoms.
↑ The central oxygen of O3 has to sometimes split its two holes into two other oxygens' electrons (= one hole is assigned to each of the lateral oxygen's electrons = increased repulsion between two oxygens' electrons with less holes in ozone ), while the oxygen of O2 can always give all its two holes to the other ( one ) oxygen (= decreased repulsion between two oxygens' electrons with more holes in O2 molecule )
The bond angle of O=O=O is 116.8o, which is close to 120o of the equilateral triangle (= vertex-center-vertex of equilateral triangle = 120o ).
In the lower-left realistic ozone model of Fig.27, the angle of m1 (= midpoint of two vertices or two electrons or holes ) - the central O2 atomic nucleus - m2 (= midpoint of another side ) is just 120o, indicating two molecular double bonds of ozone form in these directions and validating this ozone model (= due to asymmetrical distribution of ozone's three oxygen atoms, this 120o is slightly modified into 116.8o ).
In conclusion, only the quantum mechanical molecular orbital theory needs the impossible ionization in the ordinary neutral molecules, which clearly contradicts the fact of the magnitude of ionization energy values, hence, wrong.
(Fig.28) ↓ Nitrogen N2 triple bond and almost tetrahedral NH3
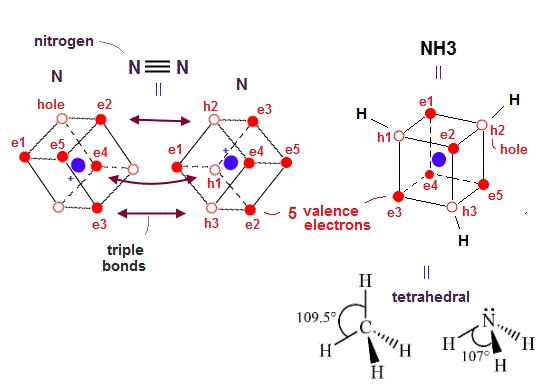
This realistic atomic model based on actually-moving electrons can also perfectly explain the actual nitrogen N2 triple molecular bonds and ammonia (= NH3 ) almost-tetrahedral structure in a natural way (= due to Coulomb electric interaction ).
Each nitrogen atom has five valence electrons which are three electrons short of full outer shells with eight electrons.
So the nitogen molecule (= N2 ) forms triple bonds between three electrons and the other N atomic three holes (= sharing three electrons between two nitrogen atoms ) like the acetylene's CC triple bond.
In the ammonia or NH3, three electrons of three hydrogen atoms can approach three holes of the nitrogen atoms and form three N-H single bonds to satisfy the octet rule or the stable hexahedral neon (= 2 × de Broglie wavelength orbit ) or helium (= 1 × de Broglie wavelength ) structures.
As shown above, three holes of the nitrogen atom are arranged tetrahedrally (= H-N-H angle is 107.8o ) like CH4 methane (= H-C-H angle = 109.5o ) due to the symmetrical Coulomb repulsion among valence electrons.
Nitrogen's five valence electrons are originally asymmetrically distributed around the nucleus, so its H-N-H angle (= 107.8o ) is slightly modified from the completely symmetrical tetrahedron of 109.5o.
↑ Quantum mechanical unphysical molecular orbital (= MO ) theory cannot use flexible orbitals whose shapes can be modified by Coulomb repulsion among electrons, because the modified-shaped orbitals (= such as H-N-H of 107.8o slightly modified from the symmetrical 109.5o ) cannot satisfy the "orthogonal or othonormal relation" strictly required by MO to avoid unnecessary Pauli repulsion.
The point is quantum mechnaical atomic orbitals such as s, px. py and pz orbitals originally have nothing to do with Coulomb symmetry or tetrahedral distribution.
Quantum mechanics tries to artificially fabricate the unnatural tetrahedral sp3 "hybrid" orbitals by forcibly combining irrelevant s and p orbitals (= which artificial manipulation of quantum mechanics causes other serious problems, as I explain later ), while the realistic moving electron model can naturally explain the tetrahedral distribution of valence electrons due to real symmetric Coulomb repulsion.
(Fig.29) NO violates octet rule or electronegativity. → Quantum mechanics is wrong.
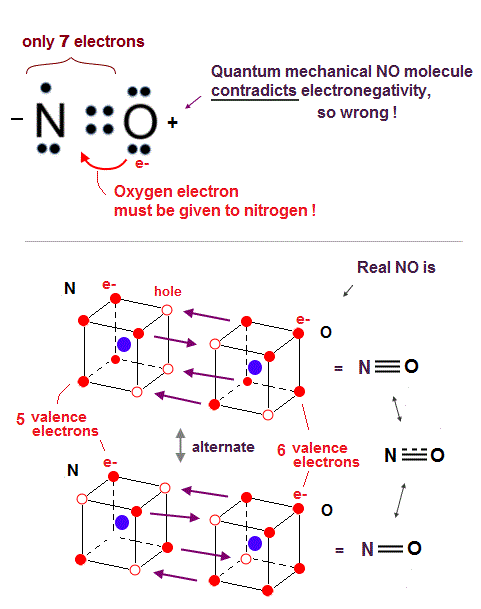
In fact, the quantum mechanical molecular orbital theory cannot explain the odd number valence electrons such as a nitrogen atom (= N with five valence electrons ).
Nitric oxide (= NO ) consisting of one nitrogen (= N ) and one oxygen atom (= O ) is a highly reactive and unstable molecule.
But NO is often observed in the air as gas at room temperature (= Not too unstable ), so we have to explain NO molecular structure by satisfying the ordinary octet rule like other stable NH3, and at the same time, we have to explain where its high reactivity comes from.
The problem is an oxygen atom needs additional two electrons, and a nitrogen atom needs additional three electrons (= there is difference ! ) to obey the octet rule.
So even if the nitrogen and oxygen share four electrons (= two electrons from oxygen, and two electrons from nitrogen ) forming double bonds, the nitrogen needs to absorb one more electron from the oxygen, which violates the electronegativity where the oxygen has more power to absorb electrons from the nitrogen.
So the quantum mechanics starts to make a contradictory claim that the nitric oxide (= NO ) disobeys the ordinary octet rule, and becomes a free radical ( this No molecule, this step 4 ), though the NO is Not too unstable to observe in the normal air.
The problem is if the nitric oxide (= NO ) conveniently violates the octet rule, and forms the normal N=O double bond where the nitrogen has only seven electrons in its valence shell, one short of eight stable electrons, it cannot explain why the actual NO bond length (= 1.15 Å ) is shorter than the normal N=O double bond length (= 1.20 Å ).
↑ This shorter NO bond length indicates NO actually forms the triple bond transiently like N2 (= which means the NO bond order is not an integer = 2.5 bond between double and triple bonds, this p.3 ), which strange bond cannot be explained by any quantum mechanical molecular orbital theory without violating electronegativity or octet rule.
On the other hand, the realistic atomic model using actually moving electrons can naturally describe this strange 2.5 bond of NO without violating electronegativity or octet rule.
As shown in the Fig.29 lower, three or two electrons are shared between nitrogen and oxygen atoms alternately in the realistic moving electron atomic model to satisfy the octet rule or Coulomb symmetrical hexahedral eight electrons' distribution without relying on unreal ionization required by quantum mechanics.
When three electrons of the oxygen approach three holes of the nitrogen, these three holes of nitrogen have to be arranged asymmetrically only on one side of the nitrogen nucleus, which Coulomb asymmetrical distribution explains why NO is an unstable molecule.
(Fig.30) The (unreal) positive ions of nitrogen atom of NO2 bond to each other in quantum mechanics !? ← Impossible ! ↓
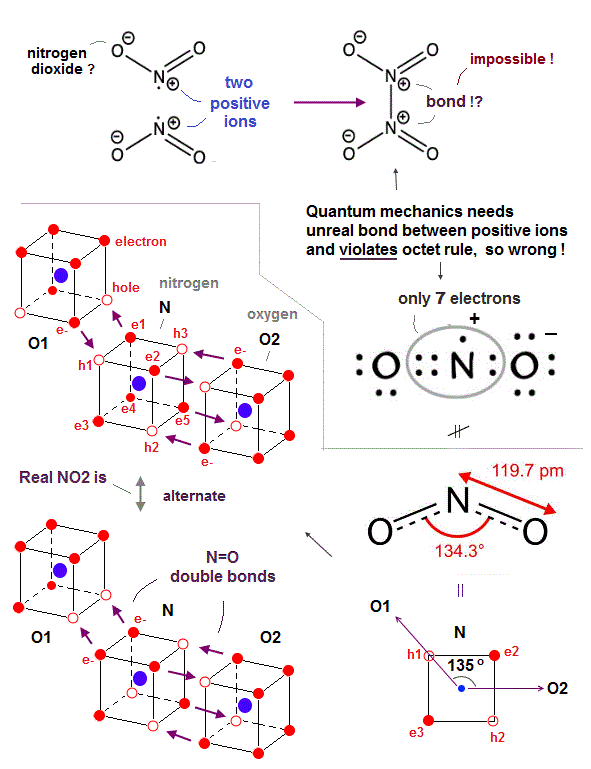
Quantum mechanical nitrogen dioxide (= NO2 ) is full of unreality and contradiction, which can disprove quantum mechanics.
First, quantum mechanical NO2 disobeys the normal octet rule, making excuses for it as "exceptions."
Though quantum mechanics makes an excuse that NO2 is an unstable free radical, NO2 can exist stably as a dark brown gas in equilibrium with N2O4 ( NO2 ↔ N2O4 ), unlike the highly unstable NO.
↑ So such a stable nitrogen dioxide (= NO2 ) must obey the octet rule contrary to the quantum mechanical baseless excuse or "exceptions".
Furthermore, quantum mechanics makes an unrealistic claim that the nitrogen atom inside NO2 becomes a (unrealistic) positive ion (= N+ ) giving its electron to a oxygen (= NO2 bond can Not generate so big ionization energy, though ), and those two positive nitrogen ions have to bond to each other to form N2O4 ( O2N+ + +NO2 = N2O4, this middle ) !
↑ This quantum mechanical ad-hoc claim is clearly impossible, because it's impossible for two positive ions to attract and bond to each other (= positive ion + positive ion = molecular bond is impossible ), hence quantum mechanical absurd claim is false.
One oxygen atom with six valence electrons and the central nitrogen atom with five valence electrons share four electrons (= two electrons from an oxygen and the other two from a nitrogen ) to satisfy this oxygen's octet rule.
The nitrogen atom needs one more electron and the other remaining oxygen atom needs two more electrons, so quantum mechanics says the nitrogen atom have to give one electron to this oxygen atom and becomes the constantly-positive ion, which contradicts the fact that N=O bond energy (= 607 kj/mol ) cannot generate such a large ionization energy of a nitrogen atom (= 1402 kj/mol ).
↑ Still the nitrogen atom has only seven electrons in its valence shell violating octet rule which requires eight electrons to be stable.
As shown in Fig.30 lower, the realistic atomic model with actually moving electrons can perfectly explain the nitrogen dioxide structure without any contradictions.
Unlike the static quantum mechanical wavefunction or electron cloud orbits, in the realistic NO2, electrons are constantly moving and alternately shared between holes of the nitrogen and two oxygens forming double (or single ) bonds, satisfying the octet rule (= filling the valence shell with eight electrons to be stable hexahedral electrons' distribution ) in both nitrogen and oxygen atoms alternately without baseless "exceptions".
The bond angle of O-N-O in NO2 is known to be 134.3o = almost equal to 135o (= 90o + 45o ) which can be perfectly explained by the realistic NO2 molecular structure, as shown in the above figure.
Two oxygen atoms (= O1 and O2 ) have exactly the same power to attract and give electrons, as shown in the same bond length of two N=O in NO2.
So the electrons' orbitals of the central nitrogen are thought to be alternately switching between the upper figure's O1=N and N=O2 relations, or when the central nitrogen provides two empty holes to the left O1 atom and one hole to the right O2 atom, the O2 atomic orbits are in mid-state (= reducing the number of electrons facing the neighboring atoms ) where O2 electrons are approaching the midpoint neutral phases of the N atom.
We explain about the N2O4 structure in nitric acid section.
(Fig.31) N atomic three holes are occupied only by two O atomic double bond. → Only the remaining 3rd single N-O bond is much weaker.
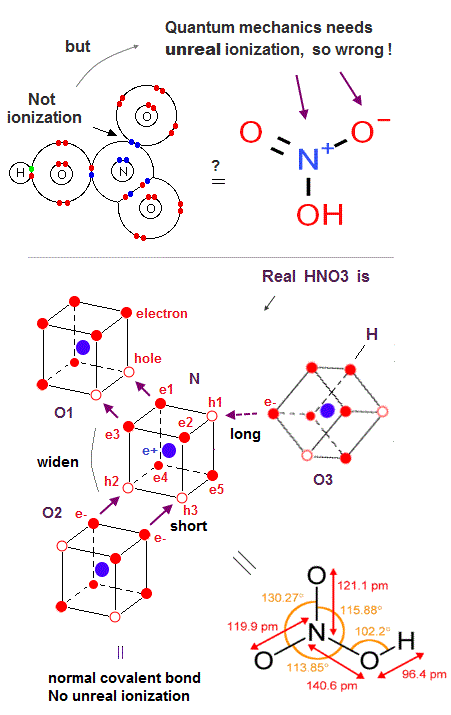
Quantum mechanical nitric acid (= HNO3 ) also needs the unreal ionization (= N+ positive ion, O- negative ion ) inside the neutral molecule, though the N=O molecular bond energy (= 607 kj/mol ) is Not big enough to cause the ionization of the nitrogen atom (= 1402 kj/mol ). ← Quantum mechanical molecule is contradictory and wrong.
The nitrogen atom (= N ) bonding to three oxygen atom (= O ) in HNO3 is compatible with the fact that the nitrogen has three holes, compared to the phosphorus atom (= P ) with the same number of five valence electrons and seven holes consisting of the 3 × de Broglie wavelength orbits that can bond to more than three atoms like phosphoric acid.
But the nitrogen's three holes can be easily occupied by two N=O double (or single ) bonds, hence, the remaining N-O single bond struggling to get a hole from the nitrogen by competing with other two strong N=O double bonds tends to be far weaker than the other two N=O double bonds.
This is the reason why N-O single bond energy (= less than 201 kj/mol ) is always far smaller than N=O double bond (= 607 kj/mol ), compared to the ratio of C-O single bond (= 358 kj/mol ) to C=O double bond (= 799 kj/mol ).
The bond angle between two N=O double bonds of HNO3 is about 130o, which is between NO2's 135o and the equilateral triangular vertex-center-vertex angle of 120o.
In Fig.31, three points of midpoint of electrons e1 and e3 - - midpoint of holes h2 and h3 - midpoint of h1 and e5 form the equilateral triangle, hence, the angle of midpoint of e1 and e3 (= direction of O1=N bond ) - N nucleus - midpoint of h2 and h3 (= direction of O2=N bond ) is 120o, and the remaining weaker O3-N single bond is in the direction of the midpoint of h1 and e5.
↑ But two stronger N=O double bonds and one weaker N-O single bond are unbalanced, hence, the shape of equilateral triangle is broken, and the angle between two strong N=O double bonds (= 130o ) become bigger than 120o of equilateral triangle.
The nitrogen's two electrons of e1 and e3 form the N=O1 double bond with the oxygen O1's two holes (= two electrons + two holes = double bond ), and the nitrogen's two holes of h2 and h3 form another N=O2 double bond with another oxygen O2's two electrons (= one N=O bond tends to occupy two holes and another N=O bond tends to occupy one hole of N atom, alternately ).
Only these two oxygens O1 and O2 approach and form the strong N=O double bonds with the nitrogen atom, so these two oxygens's abundant valence electrons tend to repel each other and their O1= N = O2 angle becomes bigger (= 130o ) than 120o.
The remaining O3 atomic abundant valence electrons, which is more distant from N atom than two O1 and O2 atoms, also has a small power to attract the nitrogen's single hole sometimes, and can form the far weaker single N-O bond.
O3 electron approaches one hole (= ex. h1 ) of the N atom either in normal hexagonal or transition (= this Fig.11-upper-left ) state less frequently than other O1 and O2 electrons, which is why the only N-O3 bond length is longer than other N-O bond length.
Anyway, N atom has three holes that provide the room for forming three bonds with three external O atoms.
↑ These bond angles are measured by looking at the nuclei of atoms of oxygens and nitrogen instead of directly looking at electrons' orbits. ← Electrons's distribution of nitrogen has to keep symmetrical hexahedral distribution, while the positions and orientations of external atomic nuclei, which repel each other, can be flexibly adjusted to obey Coulomb repulsion.
Also in the far weaker and longer N-N single bond of O2N-NO2, one N atom's electron approaches the other N's hole less frequently than other O atoms, so N-N of N2O4 is far weaker, but Not in the way of the unreal quantum mechanical bound positive ions (= N+ bound to N+ ? ← impossible ! )
This is a realistic structure of HNO3 molecule based on actually moving electrons ( or moving holes ) without relying on the quantum mechanical unreal ionization (= N+, O- ) inside HNO3 neutral molecule.
In the dinitrogen pentoxide (= O2N-O-NO2 ), the N-O single bond length (= 1.50 Å ) is longer than HNO3's single N-O bond length (= 1.40 Å ), because it is more difficult for the 3rd O3 atom of the dinitrogen pentoxide to provide its holes ( pulled by another N atomic abundant electrons in dinitrogen pentoxide, compared to hydrogen atomic single electron in HNO3 less likely pulling the 3rd oxygen's holes ) for the neighboring N atom. ← Coulomb repulsion between N-O with less holes in dinitrogen pentoxide is bigger and its N-O bond length is longer than that of HNO3.
So the influence of the 3rd more distant oxygen atom of the dinitrogen pentoxide becomes weaker than that of HNO3, and the bond angle between two N=O double bonds become wider and closer to the bond angle (= almost 135o ) of NO2.
N-N single bond length (= 1.75 Å ) of the dinitrogen tetraoxide (= N2O4 or O2N-NO2 ) is longer than the ordinary N-N single bond of 1.45 Å of hydrazine (= H2N-NH2 ).
Because in hydrazine, two hydrogen atoms (= H ) and the nitrogen atom form three single bond (= two N-Hs + one N-N ) in the tetrahedral structure like NH3.
↑ Two hydrogen atoms (= each H atom has only one electron ) of hydrazine cannot form double bond or occupy three holes of the nitrogen atoms unlike NO2 or N2O4, hence, hydrogen atomic electron's influence on the nitrogen atom (= forming N-H single bond ) is smaller than the oxygen ( = forming N=O double bond ) of N2O4.
As a result, two nitrogen atoms of hydrazine can be closer to each other due to the weaker hydrogen atom (= H pulling less holes of N, hence, Coulomb repulsion between N-N is smaller, and N-N bond is stronger and shorter ) than two nitrogen atoms of N2O4 (= oxygen atoms pulling more holes, hence, repulsion of N-N in N2O4 is stronger and N-N bond is weaker and longer ), which can explain the difference in N-N bond lengths between H2N-NH2 (= shorter N-N ) and O2N-NO2 (= longer N-N ).
(Fig.32) H-O-H angle of 104.5o is close to tetrahedral, while H-S-H angle of 92.1o is close to octahedral electrons' distribution. Why ?
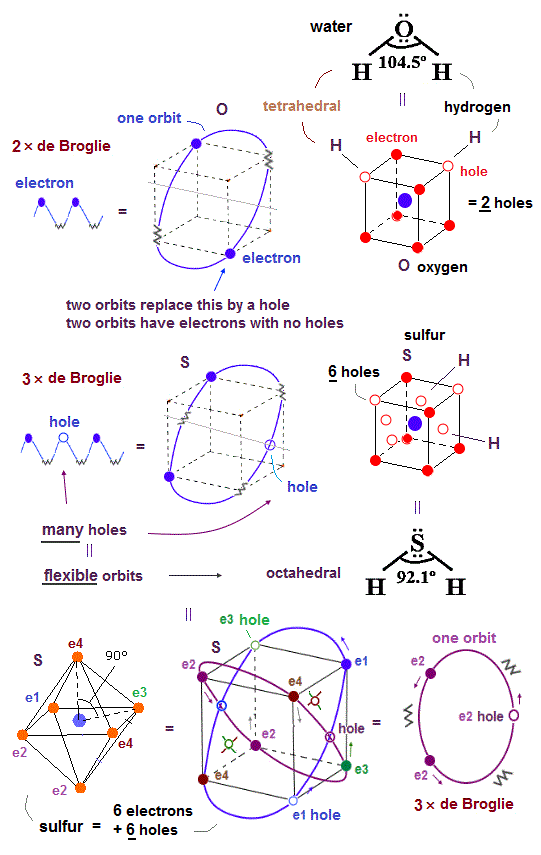
Realistic atomic model with actually-moving electrons can also perfectly explain the difference between bond angles of water (= H-O-H = 104.5o ) and hydrogen sulfide (= H-S-H = 92.5o ) based on Coulomb force symmetry.
On the other hand, the quantum mechanical unphysical atomic orbitals such as s, px, py, pz.. orbitals originally have nothing to do with Coulomb force symmetry (= one spherical s and three p orbitals in x,y,z directions is Not a symmetrical tetrahedral shape at all ).
Quantum mechanics just artificially combines those orbitals (= originally with No relation to Coulomb force symmetry ) and fabricates the ad-hoc "hybrid" sp3 orbitals to pretend the tetrahedral distribution without using real Coulomb forces or repulsions among the electron charged particles.
The bond angle of H-O-H in water is 104.5o, which is close to the symmetrical tetrahedral electrons' distribution whose atom- central atom - atom is 109.5o like other molecules such as CH4 and NH3.
Oxygen (= O ) and sulfur (= S ) have the same number of six valence electrons, so both O and S atoms should bond to two atoms for meeting the octet rule.
But only the sulfur can bond to more than two atoms as seen in the sulfuric acid (= H2SO4 ) and sulfur hexafluoride (= SF6 ).
Quantum mechanics conveniently says the sulfur violating the octet rule is one of exceptions ( this p.3 ) or "ad-hoc expansion of octet rule". ← convenient rule.
Quantum mechanics argues the sulfur could utilize "3d orbitals" to accommodate more electrons than eight electrons stipulated by the octet rule.
↑ But the contradictory quantum mechanics can never give the consistent reason why argon (= Ar ) with eight valence electrons in the same 3rd row ( n= 3 ) as sulfur in the periodic table cannot bond to more atoms, though argon also has empty 3d orbitals (= potentially accommodating an unrealistically large number of 18 valence electrons ! ) like sulfur in atoms with quantum number n = 3.
On the other hand, our realistic atomic model can perfectly fix these quantum mechanical contradictions.
Like argon in the same 3rd row of periodic table as sulfur consisting of 3 × de Broglie wavelength orbits with more holes than Neon with 2 × de Broglie wavelength, the sulfur has the total six holes which number is enough to form more than two bonds as seen H2SO4 and SF6 (= six bonds ), unlike the oxygen with 2 × de Broglie wavelength orbits containing only two holes.
The reason why argon cannot accommodate more than eight electrons is Coulomb repulsion among the symmetrical eight electrons' (= hexahedral ) distribution of argon does Not allow more electrons or bonds to attach to the inactive noble gas argon.
So we have to consider not only the octet rule, but also the actual Coulomb force repulsion or Coulomb symmetrical electrons' distribution to explain the maximum bond numbers.
Quantum mechanical unphysical atomic orbital or electron clouds do Not consider Coulomb force symmetry at all (= original s, px, py, pz orbitals are Not distributed symmetrically or tetrahedrally without artificial "hybrid" orbitals ).
This is why quantum mechanics cannot explain the difference between the sulfur violating the octet rule and the argon obeying the octet rule, though both these atoms have the same additional 3d orbitals.
So the symmetrical Coulomb force interaction and six holes of sulfur allow the sulfur to form as many as six bonds as seen in the Coulomb symmetrical octahedral shape of SF6 with 90o angle (= the sulfur's longer and flexible orbits with more empty holes can be modified to satisfy the Coulomb force symmetrical octahedral electrons' distribution ), resultantly, the bond angle H-S-H of 92.1o becomes close to 90o.
Six holes of the sulfur atom can be distributed among its six electrons symmetrically, enabling the octahedral shape of the sulfur, while the small number of two holes (= due to 2 × de Broglie wavelength orbits ) of the oxygen atom (= O ) is Not enough to be distributed among six electrons of the oxygen evenly, hence, the oxygen cannot form the stable octahedral shape (= oxygen is allowed to be only the neon-like hexahedral shape, and H-O-H angle is close to 109.5o ).
In the shorter 2 × de Broglie wavelength orbits like in Neon, for example, the electron-1 (= e1 )'s orbital direction is more strictly restricted by two e2 and e4 orbits, as shown in the e1 movement of this lower two Neon configurations, which makes the oxygen's shorter 2 × de Broglie wavelength orbits less flexible and more restricted to the hexahedral arrangement.
On the other hand, in Argon with longer flexible 3 × de Broglie wavelength with more holes, each longer orbit can be more flexibly bent and arranged, hence, sulfur's 6 valence electrons in longer orbits with 6 holes can be flexibly arranged octahedrally obeying Coulomb force symmetry among six valence electrons and six holes of sulfur, which makes H-S-H angle closer to 90o.
In the asymmetrical SF2, F-S-H bond angle (= 98o ) is bigger than 90o due to strong Coulomb repulsion between abundant valence electrons of two F atoms.
Reason why only SF6 exists and SH6 becomes unstable is explained later in Fig.34 using realistic atomic model where a hydrogen atom (= H ) with only one electron tends to be more electrically-polarized (= a positive nucleus and a negative electron of H atom is easily separated, and one side becomes positive and the other side becomes negative in each H ) than the fluorine (= F ) with more abundant 7 valence electrons uniformly distributed around F nucleus without being polarized, hence, in the SH6, when 6 electrons of 6 hydrogens approach the central S nucleus simultaneously, the central region of SH6 becomes more negative and the peripheral region of SH6 becomes more positive (= electrically polarized and unbalanced ), which is more unstable with respect to Coulomb electric force than unpolarized SF6.
The Coulomb electric force can explain why H-O-H bond angle of water is only 104.5o, and the linear 180o H-O-H bond angle (= case where two H atoms exist on just the opposite sides of O atom ) is Not allowed.
In the fictitious H2O with 180o H-O-H angle , two electrons just on the opposite sides of the central O nucleus are pushed and pulled at the same time (= two electrons of two H atoms of H2O must approach or get away from the central O atom at the same time to satisfy the octet rule where these two electrons in the same line approach and collide with each other from the opposite sides in in 180o H-O-H angle ), which becomes electrically unstable.
This can explain why is the F-S-F bond angle of SF2 also the non-linear 98o instead of the linear 180o.
In the linear F-S-F angle, when two F atoms attract two electrons of S atom at the same time (= two electrons of two F atoms approach and move away from the S nucleus at the same time to satisfy Coulomb symmetry ), these two electrons of the S atom are pulled in the opposite directions (= then, two F atoms must compete with each other to attract electrons ), which tends to make the central S atom sligtly positive (= which needs more pulling energy ), compared to the case of nonlinear F-S-F angle.
A fluorine (= F ) with abundant 7 valence electrons can stably form SF6 satisfying the octahedrally symmetrical distribution of six F atoms using 6 holes and the more flexible 3 × de Broglie wavelength sulfur (= S ) orbits, while an oxygen with the shorter less-flexible 2 × de Broglie wavelenght orbits with only two holes can bind only to two F atoms and form OF2 (= OF6 does not exist ) where F-O-F angle is closer to tetrahedral 109o.
(Fig.33) ↓ Li, Be, B, Al, metals disobey the quantum mechanical ad-hoc octet rule !
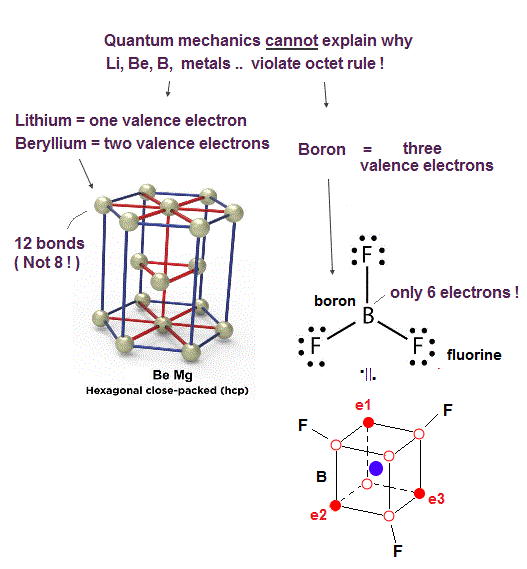
In fact, it is known that there are many atoms violating the quantum mechanical octet rules.
For example, the boron atom (= B ) of boron trifluoride (= BF3 ) is known to disobey the octet rule. but stable.
Even when a boron forms three B-F single bonds, its valence shell still has only six electrons, which is two electrons short of the octet rule.
Some physicists try to forcibly apply the octet rule to the stable BF3 by making a contradictory claim that the some 2p electrons of fluorine (= F ) could move to the boron (= B+ ), and produce an unrealistic positive F+ ion and a negative B- ion forming the impossible F-B double pi bond containing only F's electrons.
↑ But the electronegativity (= power to attract electrons ) of F is much stronger than B, hence it's impossible that the F atom with bigger power to attract electrons gives its electrons to the boron (= B ) with weaker electronegativity, and becomes an unreal positive F+ ion !
Quantum mechanics is unable to explain why its octet rule is violated in many atoms such as lithium (= Li ), beryllium (= Be ), boron (= B ), aluminum, and transition metals.
On the other hand, the realistic atomic model with moving electrons can easily explain the reason why these atoms disobey the conventional octet rule.
As shown in Fig.33, the boron (= B ) has only three valence electrons with five holes (= three 2 × de Broglie wavelength orbits + one completely empty orbit ), hence, can easily and flexibly distribute three electrons in the shape of the Coulomb force symmetrical equilateral triangle.
While it is harder for other atoms with more electrons such as carbon, nitogen, and oxygen to disobey the tetrahedral shape restricted by four orbits of 2 × de Broglie wavelength.
In the same way, the lithium (= Li ) with only one valence electron and the beryllium (= Be ) with only two valence electrons (= which means Li and Be have more empty holes and freely-usable space ) can more flexibly and change their electrons' distribution without being restricted by de Broglie wave's destructive interference from other electrons or orbits.
The quantum mechanical unphysical wavefunction or s, px, py, pz orbitals, which are orginally unrelated to Coulomb force symmetry, are static, fixed and unable to flexibly change their shapes without artificially fabricating ad-hoc hybrid orbitals which are also unable to explain the violation of octet rule.
Atoms with many holes such as Li, Be, Na, Ca .. and metals tend to become crystal-like solid structure where their electrons are constantly moving back and forth around many holes of neighboring atoms forming many bonds (= ex. beryllium useally becomes the hexagonal close packed crystal forming 12 bonds with neighboring atoms obviously violating the octet rule ).
(Fig.34) Increased Coulomb repulsion can explain unstable borane.
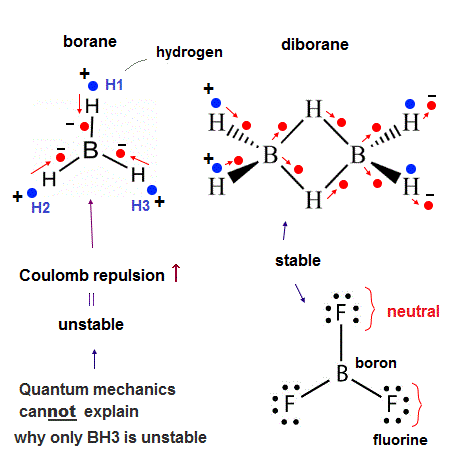
Unlike the stable BF3, the borane (= BH3 ) is unstable, cannot exist except as a diborane (= B2H6, this p.2 ). Why ?
Quantum mechanics insists that the fluorine (= F ) of BF3 unscientifically transfers its two electrons to 2p orbital of the boron (= B ), and producing a (unreal) positive F+ ion and negative B- ion. ← Impossible !
↑ This quantum mechanical preposterous explanation producing the unreal F+ ion is clearly against the fact that F atom has far stronger electronegativity (= F tends to attract other atomic electrons instead of giving its electrons ! ) than B atom, hence, quantum mechanics is intrinsically unable to explain why BF3 is more stable than BH3.
And BH3 can exist as a diborane (= B2H6 ) where each hydrogen atom (= H ) strangely forms two bonds with two B atoms (= according to quantum mechanical contradictory description ) violating the maximum valence electron number of H atom.
↑ Also in this diborane, each boron still has only seven valence electrons (= boron's 3 electrons + four H atomic electrons = 7 ) violating the octet rule, so quantum mechanics unreasonably says that each boron can share electrons with the other non-neighboring boron which is Not bonding to each other, though the distance between B-H-B in the diborane seems too long to share their electrons !
↑ So basically quantum mechanics (with unphysical mathematical tool of hybrid orbitals ) is unable to explain all the boron's molecules such as BF3 violating octet rule and borane.
In order to explain all these boron's molecules, we have to use the actually-moving realistic electrons.
As shown in Fig.34, in the unstable borane (= BH3 ), three electrons of three hydrogen atoms must approach the boron nucleus simultaneously obeying the symmetrical triangular distribution where three valence electrons of the boron move to the regions just between H atoms symmetrically (= which is also equilateral triangular distribution ).
Each hydrogen atom (= H ) has only one negative electron and one positive nucleus (= proton ), so when three electrons move toward the boron nucleus, the entire BH3 becomes strongly electrically unbalanced or polarized (= the center of BH3 is negative and the edge of BH3 is positive ) against the Coulomb force balance (= repulsion among electrons around the central boron becomes stronger ).
Unlike a H atom with only one electron (= easily polarized as seen in hydrogen bond ), the fluorine (= F ) atom of BF3 has as many as seven valence electrons, so even when one electron of F atom moves toward the central boron atoms, other six electrons of F atom move toward the opposite side of the F's nucleus, and the F atoms remains electrically-neutral which does not cause the unbalanced Coulomb repulsion or the clash among electrons around the central B atom like unstable BH3.
↑ And F atoms have the strong electronegativity, hence, F atomic electrons strongly bound to F's 7e+ positive nucleus are less likely to approach the distant S atomic nucleus, instead, each F atom tends to grab a S atomic electron (= transiently, though ).
↑ This is a realistic reason why only BF3 exists and BH3 cannot exist.
The same explanation can apply to the reason why only SF6 exists and SH6 does not exist (= quantum mechanics tries to explain this using the illegitimate expansion or exception to octet rule ).
In diborane (= B2H6 ), four H atoms binding to each B atom are almost tetrahedrally arranged (= reducing Coulomb repulsion ) instead of existing in the same plane, unlike triangular BH3 in the same plane (= increasing Coulomb repulsion ).
As shown in Fig.34, in the B2H6, when two electrons of two left-side H atoms approach the left B atom, two electrons of this B atom are pushed toward two central H atoms (= these two pushed electrons of B atom can approach the two left-side H atomic nuclei when those H-atomic electrons move to the opposite side of the H nuclei, alternately ), which can avoid the increase in Coulomb repulsion or the clash among electrons.
In the equilateral triangular BH3, if two electrons of two H1 and H2 atoms approach the central B atom, and only the remaining electron of H3 atom moves away from the central B atom (= to avoid Coulomb repulsion ), one electron of B atom is attracted toward the exposed H3 nucleus, and other two electrons of B atom are pushed toward H1 and H2 atoms (= three electrons of B atom must be always distributed in the triangular way due to Coulomb force symmetry ) clashing with two electrons approaching from H2 and H1 atoms, which makes only BH3 unstable.
(Fig.34') electron-hole pair forms covalent bonds between two atoms.
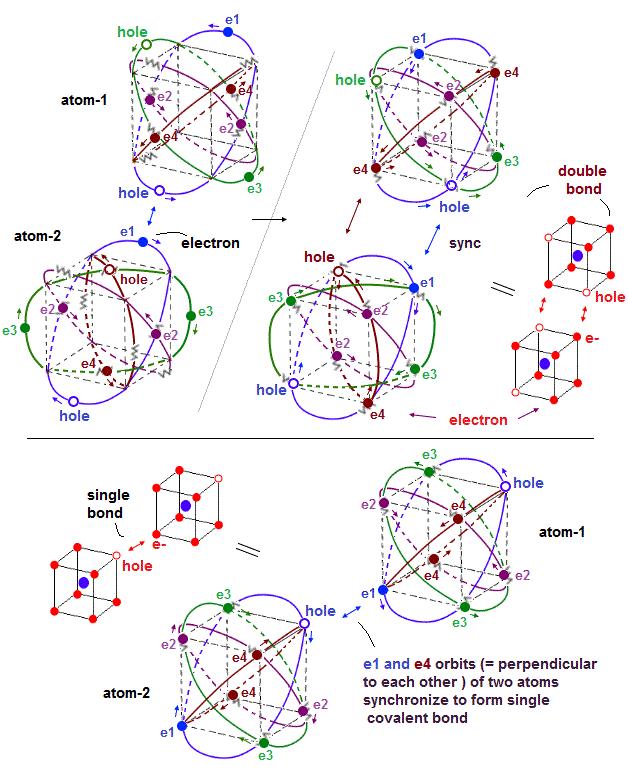
When two atoms (= atom-1 and atom-2 ) form covalent bonds, holes of one atom have to approach and synchronize with corresponding electrons of the other atom by Coulomb attraction.
The upper figure of Fig.34' is the double bond between two atoms-1 and 2 where electron-1 (= e1 ) of atom-2 synchronizes with a corresponding hole of atom-1 causing strong Coulomb attractive covalent bond.
Not only the electron-e1-hole pair, the opposite de Broglie wave phases of e4 and e3 orbits of two atoms synchronize with each other by flowing in the same direction.
In the lower figure of Fig.34', a pair of electron-1 (= e1 ) of atom-1 and a hole of atom-2 forms a single covalent bond by Coulomb attraction.
Some electrons sometimes need to jump into holes to create new holes for avoiding other electrons by Coulomb repulsions especially in atoms with many valence electrons such as fluorine (= F ) and oxygen atoms, which stronger repulsive force among more electrons makes F-F bond energy smaller and weaker than other bonds such as C-C bond.
While (four) electron orbits of each atomic valence electrons keep almost symmetric to avoid destructive interference de Broglie wave, external atoms forming covalent bonds can more flexibly change their positions, keeping covalnet bonds between electrons and holes (= to satisfy Coulomb repulsive symmetry among external atoms ), as long as their orbits keep parallel to the corresponding orbits between two atoms ( e1-e1, e3-e3, e4-e4 orbits of atom-1 and atom-2 in the upper figure ) forming covalent bonds.
(Fig.35) ↓ Linear and circular motions.

As shown in the Broglie wave interference of an electron in a linear motion, the influence of each de Broglie wave reaches very distant area = 5~6 atomic distance.
But when an electron moves around a nucleus in a circular motion, the area the de Broglie wave reaches is smaller.
Because when an electron moves with a velocity of v around an nucleus in a circular orbit with the radius r, in the point which is 3r distant from the nucleus, de Broglie wave phase must move three times faster (= 3v ) to keep up with the inner electron moving at a speed of v, which is difficult.
So in the points which are some distance away from the inner electron's circular orbit, the electron's de Broglie wave opposite phases (= crest and trough ) are mixing and canceling each other due to being unable to keep up with the much-more-quickly-changing inner electron's circular orbital de Broglie wave phases.
As a result, in the area outside the inner electron's circular orbits, Pauli repulsion is fadeing away, as the distance from the inner electron's orbit is longer.
This area where the inner electron's orbital Pauli repulsion reaches must be determined by experiments.
Considering Pauli repulsion (= caused by destructive interference between de Brogle wave phases ) between two hydrogen atoms bound to different atoms ( the non-convalent distance between two hydrogen atoms H-H is about 1.3 Å ), we can estimate the influence of each electron's de Broglie wave reaches as far as the point which is less than 3r distant from the nucleus.
(Fig.36) 2 × de Broglie wavelength orbits "aim" at four orbits like Neon.
As I said, the orbit of two de Broglie wavelength contains two symmetrical midpoint lines with zero phase. So the total four orbits ( 2 × 2 perpendicular orbits ) become the most stable.
Because as shown in Neon, when four orbits are included, they are completely symmetrical with respect to both Coulomb and de Broglie waves.
(Fig.37) Oxygen bonds, H2O.
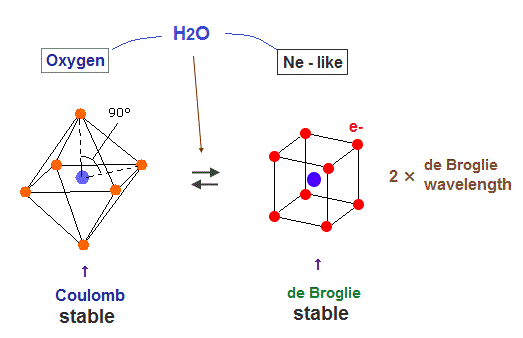
Oxygen atom contains six valence electrons, so regular octahedral shape is most stable with respect to Coulomb repulsion. But as shown in Fig.25, four orbits with eight electrons are symmetrical and stable as "de Broglie waves".
So oxygen also aims at Neon-like hexahedral structure to be stable in both Coulomb and de Broglie waves .
As a result, the bond angle of H2O (= 104.5o ) is between octahedron (= 90o ) and tetrahedron (= 109.5o )

2022/6/13 updated. Feel free to link to this site.