Quantum mechanical Pauli exchange energy is unreal.

  Home page

Quantum mechanical spreading probability wavefunction without really moving electrons cannot use real Coulomb electric force for molecular bonds.

(Fig.1)  ↓ No Coulomb force between two quantum wavefunctions.

Unreal quantum mechanical molecules.

Quantum mechanical unphysical spreading electron cloud without actually-moving electrons cannot exert Coulomb attraction for forming molecular bonds.

In fact, quantum mechanical unphysical probability wavefunction always spreading in all space as electron clouds in useless Schrödinger equation is unable to use ordinary Coulomb electric force for forming covalent molecular bonds.

As shown in the upper figure-right, in the realistic atomic orbit such as successful Bohr's atom, an electron is actually moving around, approaching the other positive nucleus and avoiding the other negative electron to form stable molecular bond by ordinary real Coulomb electric force.

On the other hand, quantum mechanical unphysical probability wavefunction or electron cloud must always spread out symmetrically around the nucleus to infinity by fantasy superposition or parallel universes, which cannot express real moving electrons.

No real Coulomb force in quantum mechanics.

Unphysical quantum mechanical spreading electron cloud in parallel universes cannot exert real Coulomb force to form molecular bonds.

The symmetrically-spreading quantum mechanical probability wavefunction or electron cloud is like the symmetrical spherical charge which average electron's position is at the same position as the central nucleus, which generates the zero net charge by the negative electron and positive nucleus canceling each other.

If the quantum mechanical spreading wavefunction tries to shrink only to one position, the localized shrunk wavefunction or de Broglie wave becomes sharper (= de Broglie wavelength is shorter ), and the electron's kinetic energy drastically increases, which disagrees with experimental atomic energies.

As a result, the unphysical quantum mechanical spreading probability wavefunction, which cannot use the real Coulomb force for forming molecular bonds, has to rely on another unphysical energy called exchange energy allegedly caused by lower kinetic energy (= higher kinetic energy is unreal quantum Pauli principle ).

Each electron must exist in all different atoms unrealistically in quantum mechanical molecules due to unphysical antisymmetric wavefunctions.

(Fig.2)  ↓ An electron-1 must exist in two different H atoms-A and B simultaneously.

An unreal electron exists in different atoms

Quantum mechanical unphysical molecular bond needs a single electron to exist in different atoms simultaneously by parallel worlds.

For unsolvable Schrödinger equations that cannot predict anything, quantum mechanics has to artificially choose unphysical antisymmetric wavefunctions where each electron must exist in all different atoms-A,B,.. simultaneously by parallel worlds, which forbids each atom from having its shape or boundary, so hampers technology.

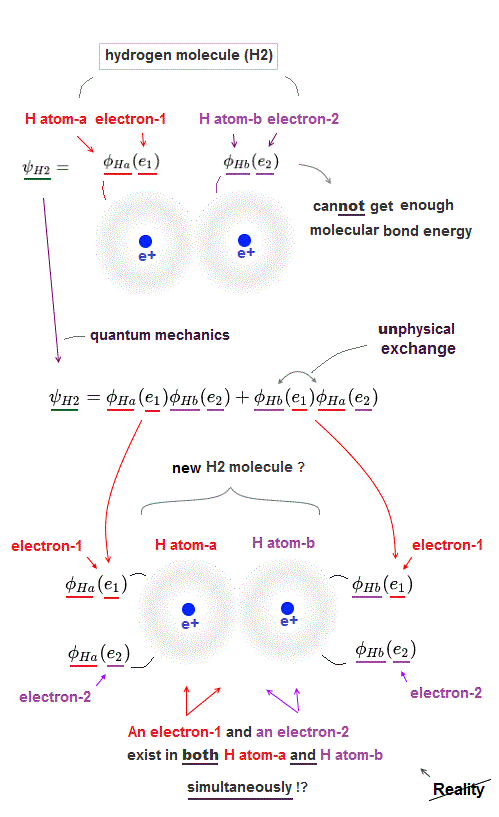
Also for unphysical quantum mechanical molecules to generate covalent molecular bond energy (or strong Pauli repulsive energy ), they require each quantum mechanical electron to exist in all different atoms in a molecule simultaneously to generate the fictitious exchange kinetic energy-molecular bonds.

For example, in the upper hydrogen H2 molecule consisting of two H atoms-A and B, both the electron-1 and electron-2 must exist in two different H atoms-A and B simultaneously ( this p.3,  this p.11,  this p.4 ).

φ_A ( r1 ) means the electron-1 existing in H-atomic wavefunction φ_A.
φ_B ( r1 ) means the electron-1 existing in H-atomic wavefunction φ_B ( this p.18 ).

H2 molecular Hamiltonian H or total energy consists of two electrons' kinetic energy expressed as space derivative (= de Broglie wave ) and Coulomb electric energy terms among two H atomic nuclei-A, B and two electrons-1, 2, as shown above.

Quantum mechanical molecular bonds caused by unphysical (anti)symmetric wavefunctions where each electron exists in all different atoms generating fictitious exchange energy decreasing kinetic energy without real force.

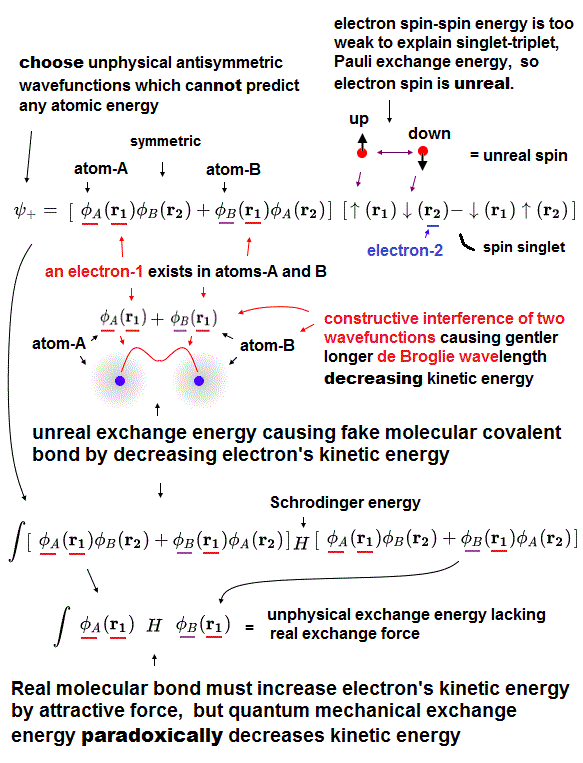
(Fig.3)  Real molecular bond attraction should increase electrons' kinetic energy, which contradicts the unreal quantum mechanical molecular bond exchange energy based on decreased kinetic energy

Quantum mechanical unphysical antisymmetric wavefunctions for unreal Pauli principle.

Quantum mechanics has to choose fake antisymmetric wavefunctions for unsolvable Schrödinger equations that cannot predict Pauli principle energy.

Quantum mechanical Schrodinger equations are useless, unsolvable, unable to predict energies for atoms or molecules.

Physicists have to artificially choose the unphysical antisymmetric wavefunctions as these fake trial wavefunctions to express the unphysical Pauli exchange energies in quantum approximate variational methods such as Hartree-fock (= artificial chosen quantum mechanical wavefunctions cannot predict Pauli exchange energy ).

A single electron exists in different atoms

Each electron must exist in all different atoms unrealistically in quantum mechanical molecules or unphysical (anti)symmetric wavefunction.

Quantum mechanics unrealistically demands each electron-1 and 2 must exist in two different H atoms-A and B to form fictitious H2 molecular covalent bonds in the artificially-chosen fake antisymmetric wavefunction for unsolvable Schrodinger equations.

To form fake quantum molecular attractive covalent bonds, symmetric wavefunctions (= spin part is up-down singlet antisymmetric or bonding = so the total is antisymmetric wavefunction ) are necessary ( this p.3-4 ).

Electron spin is unreal

Unreal electron spin-spin magnetic energy is too weak, disagrees with experiments, so they created fictitious exchange energy for unreal quantum Pauli principle and molecular bonds.

Electron spin is unreal, and electron spin-spin magnetic dipole energy is too weak (= just 0.0001 eV, this-p.10-left-2nd-paragraph ) to cause singlet-triplet exchange energy splitting (> 1eV, this p.3-middle,  this 3s3p singlet ¹p and triplet ³p energy difference is 13140cm-1 = 1.629 eV ) or Pauli exchange energy (> 10eV ), so electron spin is unreal, unnecessary.

By putting H2 molecular ( Schrodinger equation's ) total energy Hamiltonian (= H ) between these (artificially-chosen) two symmetric wavefunctions (= ψ₊ ) where each electron-1 and 2 exists in two different H atoms-A and B and integrate them, we can get two different integrals called Coulomb energy integral and (unphysical) exchange energy integral ( this p.3-4,  this p.14,  this-p.3-p.6 ).

Unreal quantum molecules with No Coulomb

Quantum mechanical molecular bonds are Not caused by real Coulomb electric force but by unphysical exchange energy.

Coulomb energy integral is the normal integral where each electron-1 (or electron-2 ) consists of two same H atomic wavefunctions like ∫φ_A(r1)φ_A(r1) and ∫φ_B(r1)φ_B(r1).

Unphysical exchange (= resonance ) energy integral consists of two different H atomic wavefunctions like ∫φ_A(r1)φ_B(r1) and ∫φ_B(r1)φ_A(r1).

This unphysical exchange (= resonance ) energy integral is necessary to cause fictitious quantum mechanical molecular bonds (or Pauli repulsive antibonding ), and the ordinary Coulomb energy (integral) has No power to form molecular attractive bonds ( this p.3,  this-lower-Fig.2,  this p.4-5,  this p.4-5-Fig.1 ) or Pauli repulsive antibonding.

This (or this )-p.3-last~p.4 say  -- Exchange, No Coulomb force
"and J and K are Coulomb and exchange integrals"
"but the contribution of J (= Coulomb energy ) is far smaller (in absolute value) than that of K (= unphysical exchange energy integral,  this-p.15 )"

Quantum molecular bond by kinetic energy

Quantum mechanical molecular bonds are caused by unphysical exchange energy decreasing kinetic energy due to constructive interference of symmetric wavefunctions (= gentler de Broglie wave ).

In this symmetric wavefunction (= constructive interference of two wavefunctions ), the total wavefunction becomes gentler, which means the total de Broglie wavelength becomes longer, and electron's kinetic energy decreases ( this-p.12-conclusion ).

This decrease in electron's kinetic energy is the driving force of forming molecular attractive covalent bonds caused by unphysical exchange energy.

This-p.1-1st-paragraph says  -- Decreased kinetic energy
"chemical bond formation is driven by a decrease in electron kinetic energy."

Textbooks hide inconvenient truth.

Quantum mechanical molecular bonds are due to fake kinetic energy decrease instead of Coulomb force.

We often see the wrong explanation that higher electron's density between two H atoms may cause decrease in Coulomb electric energy and molecular attractive bonds.

But even if Coulomb potential energy decreases, kinetic energy increases to conserve the total energy, the molecular attractive bonds cannot be formed, so the electron's lower kinetic energy even in the lower Coulomb potential energy region is the reason of quantum mechanical unphysical exchange molecular bonds.

Kinetic energy decrease is the origin of unphysical quantum mechanical molecular bond.

This or this-p.4-left-last-paragraph~right says
"Many textbooks are saying that chemical bonding is a result of the accumulation of density in the binding region. This is a deceptive statement, because the origin for the charge accumulation is Not given"

"This author showed that the kinetic energy plays a paradoxical role in the chemical bond formation"

"Ruedenberg has shown that it is actually a decrease of T (= kinetic energy ) which accompanies the charge accumulation in the bonding region"

Quantum molecular bonds are false.

Real attraction should increase electron's kinetic energy, which contradicts quantum mechanical molecular bonds caused by the decreased kinetic energy in unphysical exchange energy.

This quantum mechanical molecular bond exchange energy based on lower kinetic energy is unphysical and wrong ( this p.11 ).

Because if the real attractive force is working between two atoms, electrons are attracted and accelerated toward the other atoms, so electrons' kinetic energies should increase instead of decrease (= when two atoms repelling each other, electrons decelerate, and kinetic energy should decrease ).

↑ Quantum mechanical exchange energy based on kinetic energy violates basic physical principle, so wrong.

This contradictory quantum mechanical exchange energy due to kinetic energy change lacks real exchange force or physical reality ( this p.9-upper,  this p.8-last,  this p.5,  this p.8-right-Discussion ).

Quantum mechanical molecular bonds are unreal, Not conserving total energy = lower kinetic energy even in lower Coulomb potential energy region.

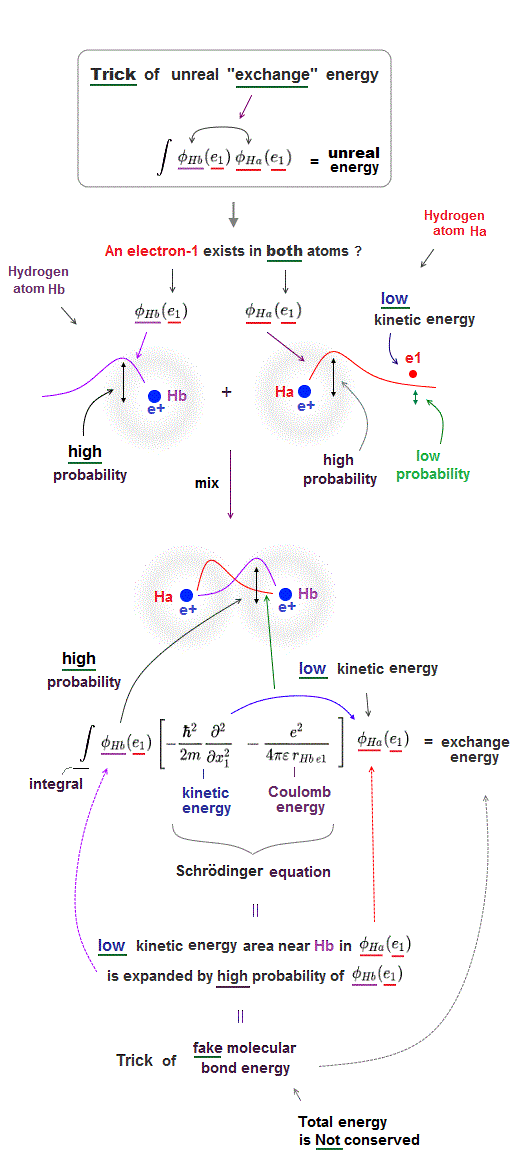
(Fig.4)  In unreal quantum H2 molecule, even when an electron-1 approaches the other H-atom-B's positive nucleus decreasing Coulomb potential energy, its kinetic energy keeps decreasing, violating energy conservation = trick of unphysical exchange energy.

Hydrogen (= H ) atom conserves total energy.

Schrödinger equation is solvable only for one-electron hydrogen (= H ) atom which is the only atom conserving the total energy in any electron's positions.

No quantum mechanical Schrödinger equations are solvable except for one-electron hydrogen (= H ) atom ( this or this p.21-upper ).

In only this solvable H atom, the total energy E, which is the sum of electron's kinetic energy expressed as derivative and Coulomb potential energy, is always constant and conserved in any electron's positions ( this-p.2-upper,  this p.2-1st-paragraph ).

So in H atom, as the electron-1 is farther away from the H atom-A's positive nucleus, it increases Coulomb potential energy and decreases electron's kinetic energy to keep the constant and conserved total energy E.

Quantum H2 molecule Not conserving energy

Quantum mechanical unreal molecular bond relies on lowering kinetic energy even in lower Coulomb potential energy regions, Not conserving total energy, so false.

In molecules such as hydrogen molecule (= H2 ) and hydrogen molecular H+ ion whose Schrödinger equations are unsolvable ( this p.4-lower ), quantum mechanics must artificially choose fake trial wavefunctions or basis sets.

In H2 molecule (or H+ molecule ), two hydrogen atomic 1s wavefunctions (= H-atom-A and B ) are used in the chosen trial wavefunctions ( this p.4,  this p.6-7,  this p.3 ).

As shown in the upper figure, in H2 molecule, even when the electron-1 approaches the other H atom-B's positive nucleus decreasing Coulomb potential energy, the electron-1's kinetic energy keeps decreasing due to the use of the H-atom-A's 1s wavefunction.

This is clearly violation of total energy conservation law (= both kinetic and Coulomb potential energies decrease ! ), so quantum mechanical molecules are false and unphysical.

Quantum exchange integral lowers kinetic energy.

Quantum mechanical molecular bonds rely on unphysical exchange energy integral which further lowers kinetic energy by illegitimately violating energy conservation.

So decrease in the kinetic energy is enhanced in exchange energy where the lower kinetic energy region of H atom-A (or H atom-B ) is expanded by larger probability amplitude of the other H atom-B (or H atom-A ) wavefunction near the other H atomic nucleus.

This is the trick of how the unphysical quantum mechanical exchange energy decreases the total energy (= by decreasing kinetic energy and violating energy conservation law, so false ) to form molecular attractive bonds.

Quantum mechanics uses unphysical antisymmetric wavefunctions causing Pauli principle exchange energy increasing kinetic energy by each electron existing in different atoms causing destructive interference of de Broglie wave.

(Fig.5)  The single electron-1 (or electron-2 ) must unrealistically exist in both H atom-A and H atom-B simultaneously to generate Pauli repulsive exchange energy.

Unreal quantum Pauli antisymmetric wavefunction

Quantum mechanical Pauli repulsive energy is due to unphysical antisymmetric wavefunction cansuing exchange energy increasing kinetic energy.

For unsolvable Schrodinger equation that cannot predict anything, physicists artificially choose antisymmetric wavefunction where the signs of two terms of exchanging two H atom A and B wavefunctions are different (= spin is symmetric or triplet like up-up or down-down ), which can obtain Pauli repulsive exchange energy or antibonding.

↑ But (unreal) electron spin-spin magnetic energy is too weak to cause strong Pauli repulsive exchange energy, so electron spin is unreal, irrelevant ( this-p.6-2.4 ).

The sign of this antisymmetric wavefunction's exchange energy integral is negative = opposite to the molecular bond attractive exchange energy integral.

So in this (negative) Pauli repulsive exchange energy integral with the opposite sign of molecular attractive bond exchange energy caused by decreased kinetic energy, electron kinetic energy increases (= without decreasing Coulomb potential energy, so total energy is Not conserved in this, either,  this-p.1-2. ).

Quantum mechanical Pauli principle repulsion is Not a real force.

Quantum mechanical Pauli principle is caused by unreal exchange energy increasing kinetic energy lacking real exchange repulsive force.

This-p.9-Fig.1.2 and p.10-1.5 say  -- Pauli increases kinetic energy
"The effective repulsion due to Pauli exclusion stems from the change in the curvature of the wavefunction due to the requirement for antisymmetrization in fermion systems. Higher wavefunction curvature (= shorter de Broglie wavelength ) leads to a higher kinetic energy"

"Pauli exclusion does Not produce a force in the traditional sense"
"We call it an exchange force but it is Not really a force at all - No physical agency is pushing on the particles"  ← unreal

↑ Quantum mechanical Pauli exclusion repulsion caused by (pseudo-)kinetic energy increase (= unreal exchange energy ) is Not a real force, which fact disproves quantum mechanics.

Textbooks hide Pauli increasing kinetic energy.

Unreal quantum mechanical Pauli principle is caused by electrons increasing kinetic energy compared to Coulomb energy.

Textbooks often use the wrong explanation "antisymmetric (= antibond ) wavefunctions (= destructively-interfering wavefunctions ) decrease the electrons' probability between atoms, which may increase Coulomb electric potential energy and cause Pauli repulsion", which ignores kinetic energy change ( this-p.2-upper ).

↑ This textbooks' explanation is wrong, because the total energy is the sum of Coulomb electric potential energy + electrons' kinetic energy.

So even when the electric potential energy increases, the total energy is unchanged if the kinetic energy also decreases to conserve the total energy.  ← This does Not happen in the contradictory quantum mechanical Pauli principle exchange energy violating energy conservation law.

↑ Actually, the positions of the lowest Coulomb electric potential energy is near each atomic nucleus, rather than the area between two atoms, contrary to the textbooks' explanation.

As a result, the quantum mechanical unphysical Pauli repulsive energy is caused by the drastically-increased kinetic energy compared to the Coulomb electric potential energy change by violating total energy conservation.

Kinetic energy increase in antibonding causes unreal Pauli principle.

Unreal quantum mechanical Pauli principle repulsive energy is due to kinetic energy increased by antisymmetric wavefunctions shortening de Broglie wavelength.

This increase in electron's kinetic energy is the driving force of unphysical quantum mechanical Pauli repulsion ( this p.9-10,  this p.6-4th-paragraph,  this or this-introduction-3rd-paragraph ).

This p.3-left-middle says  -- Pauli principle increasing kinetic
"Pauli repulsion originates in the kinetic energy increase"

↑ Pauli antisymmetric wavefunctions have steeper slope that increases kinetic energy by shorter de Broglie wavelength ( this or this p.13-2nd-paragraph ).

This-p.7-4th-paragraph says  -- Pauli increases kinetic energy
"The opposite holds for the antibonding state,... because of its large 0.316 Eh kinetic energy, despite an attractive −0.106 Eh potential energy contribution (both relative to H + H+). The large kinetic energy is a consequence of the node in the wave function,.. a region of large gradients"

Quantum Pauli principle is wrong.

Real repulsion should decrease kinetic energy, which contradicts quantum mechanical Pauli repulsion based on increased kinetic energy.

There is No real repulsive force or force carrier in this quantum mechanical Pauli repulsive exchange energy ( this or this-p.9-upper,  this-p.5-upper ) caused by increased kinetic energy.

This-(4) says -- No exchange force
"The exchange interaction is sometimes called the exchange energy or exchange force. However, it is Not a true energy or force."

This-p.2-(c) says -- Unreal exchange force
"Anti-symmetrizing a wavefunction actually pushes the particles apart, while symmetrization pulls them closer together. This effect actually behaves like an effective force / pseudo-force, and is sometimes called the exchange force (= unreal pseudo-force )"

If the real repulsion is exerted between two atoms, electrons must be decelerated or slow down (= decrease kinetic energy ) by repulsion from the other atom, instead of increasing kinetic energy.

So quantum mechanical Pauli repulsive exchange energy allegedly caused by the increased kinetic energy disagrees with physical principle, so unreal.

Quantum mechanical Pauli antisymmetric wavefunctions are wrong, cannot conserve total energy nor satisfy Schrodinger equations

Quantum mechanical unphysical exchange energy contradicts the normal Coulomb electric energy, so unreal.

(Fig.6)  In normal Coulomb energy integral, only Coulomb repulsion between H atom-A's electron and H atom-B's electron exists, but in abnormal exchange energy, unphysical repulsion between electrons existing in the same H atom-A (or H atom-B ) appears, which is self-contradictory.

Exchange electric energy is Not a real thing.

Quantum mechanical Coulomb energy says electrons-1 and 2 exist in different atoms-A and B, but its exchange energy paradoxically says electron-1 (and 2 ) exists in both atoms-A and B unrealistically.

When integrating the (anti-)symmetric wavefunctions with H2 molecular Hamitonian energy, we can obtain the normal Coulomb electric repulsive energy between the electron-1 existing in H atom-A (or H atom-B ) and the electron-2 existing in H atom-B (or H atom-A,  this-p.3-(18),  this-J ).

Coulomb energy:  ∫φ_A(r1)φ_A(r1) * φ_B(r2)φ_B(r2)  or  ∫φ_A(r2)φ_A(r2) * φ_B(r1)φ_B(r1)

↑ In the normal Coulomb energy integral (= obeying the original quantum mechanical electrons wavefunctions' probability expressed as a square of the same wavefunction amplitude ), when the electron-1 exists in H-atom-A's wavefunction, the other electron-2 must exist in H-atom-B's wavefunction (= electrons-1 and 2 must exist in different atoms in normal Coulomb energy integral ).

But in the abnormal exchange energy integral,

Exchange energy:  ∫φ_A(r1)φ_B(r1) * φ_A(r2)φ_B(r2)

↑ As seen here, in the abnormal exchange energy integral, even when the electron-1 exists in H atom-A's wavefuntion, the electron-2 can exist in the same H atom-A's wavefunction, which contradicts the normal Coulomb electric energy ( this-p.15,  this-p.3 ), because each electron must always exist in both different atoms-A an B in the unreal exchange energy.

This is clearly self-contradiction, and shows quantum mechanical exchange energy is Not a real thing.

Quantum mechanical Pauli principle based on unreal kinetic energy change cannot conserve total energy nor predict energy.

(Fig.7)  Electrons in H2 molecules cannot conserve the same total energy E in different positions in unreal quantum mechanical Pauli principle.

Quantum mechanics cannot conserve energy.

Total and kinetic energies are different (= Not conserved ) in different positions in quantum mechanical molecules.

In the upper Fig.7, Two hydrogen atoms of H-atom-A and H-atom-B form a H2 molecule by covalent bond, and H-atom-B and other H-atom-C repel each other by Pauli repulsion.

The total and kinetic energy of the same electron in this H2 molecule must become lower between H-atoms-A and B (= causing fictitious attractive bond energy ), and become higher between H-atoms-B and C (= causing unreal Pauli repulsion ).

Each electron feels the same Coulomb energy in positions between H-atoms-A and B and positions between H-atoms-B and C.

So the total energy = Coulomb energy (= same ) + kinetic energy (= lower or higher in different positions ) is Not conserved nor constant.

It means Schrodinger equations of quantum mechanical molecules are unsolvable (= cannot conserve the constant total energy E in different positions ), cannot predict any molecular energy.

Quantum mechanical Pauli antisymmetric wavefunction cannot become true solutions of Schrödinger equations.

(Fig.8)  ↓ Pauli antisymmetric wavefunction is wrong, cannot satisfy Schrödinger equation.

Pauli principle contradicts Schrödinger equation.

Quantum mechanical Pauli antisymmetric wavefunctions cannot satisfy Schrödinger equations.

We can prove quantum mechanical Pauli (anti)symmetric wavefunctions cannot become true solutions of Schrödinger equations, so wrong.

As shown in the upper Fig.8, quantum mechanical Pauli (anti-)symmetric wavefunctions cannot satisfy Schrödinger equation (= left-side equation contains an electron-1 in atom-A wavefunction, and right-side equation contains an electron-1 in atom-B wavefunction, which are different equations ).

It means quantum mechanics cannot solve Schrödinger equation nor predict molecular energy.

Feel free to link to this site.