---

トピックス

• 人の目の高さから見える水平線迄の距離は約4km
• Raspberry PI Pico
• JR奈良線第2期複線化竣工
• Spiceによる感染症数理モデルのシミュレーション

---

SIRモデル^*1

下式が感染症の数理モデルの基本であるSIRモデルの連立微分方程式で、時間(t)の関数はそれぞれ

• 感受性(susceptible)
• 感染性(infectious)
• 隔離や回復(removed/recoverd)

の各グループを表します。

$\frac{\mathrm{d}S\left(\mathrm{t}\right)}{\mathrm{d}t}=-\beta S\left(\mathrm{t}\right)I\left(\mathrm{t}\right)$
$\frac{\mathrm{d}I\left(\mathrm{t}\right)}{\mathrm{d}t}=\beta S\left(\mathrm{t}\right)I\left(\mathrm{t}\right)-\gamma I\left(\mathrm{t}\right)$
$\frac{\mathrm{d}R\left(\mathrm{t}\right)}{\mathrm{d}t}=\gamma I\left(\mathrm{t}\right)$

二番目の式を変形して

$\frac{\mathrm{d}I\left(\mathrm{t}\right)}{\mathrm{d}t}=\left(\beta S\left(\mathrm{t}\right)-\gamma \right)I\left(\mathrm{t}\right)$

感染が流行、つまり $\frac{\mathrm{d}I\left(\mathrm{t}\right)}{\mathrm{d}t}>0$ になるのは
$\frac{\beta S\left(\mathrm{t}\right)}{\gamma }>1$
のときで、また初期条件 $S\left(\mathrm{0}\right)=1$ から
$\frac{\beta }{\gamma }=1$
が流行の閾値で $\raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.$ は基本再生産数(R₀)と定義されます。

SIRモデルの連立微分方程式にはS(t)とI(t)の積の項が含まれます。この積の項がなければ、現代制御理論の状態方程式のように線形な連立微分方程式として解法できそうですが、S(t)I(t)の項があるSIRモデルでは、β とγ のパラメータを適当に設定した上でシミュレーションという手段をとらせざるを得ないようです。

アナログコンピュータ

コンピュータといえばデジタルそのもので、その対極としての古臭さく非効率なアナログというような認識からは、 アナログコンピュータという名称それ自体が論理矛盾のように受け止められるかもしれませんが、今から半世紀前、 パソコンどころかマイコン(マイクロプロセッサや組み込み用のマイクロコントローラ)すら存在していない時代に、アナログコンピュータという装置が確かに存在していました。

実際のアナログコンピュータはどのようなものであったかというと、演算増幅器(オペアンプ)、抵抗(ポテンションメータ)、コンデンサで構成された積分器や加算器等を組み合わせた回路によって微分方程式や制御系の伝達関数をシミュレーションする装置で、工業系の学校で教育用にも使用されていたようですが、本来の目的はリアルタイムな大砲の弾道計算であったという説もあります。

アナログ半導体の代表格オペアンプ(OP-Amp)の名称はOperational Amplifier(演算増幅器)の略称なのですが、元々の由来はアナログコンピュータにあるのではないでしょうか。オペアンプのアプリケーションにステート・バリアブル・フィルタとかバイクワッド・フィルタと呼ばれる回路があります。これらの回路では積分器や加算器を組み合わせて希望する系の伝達関数を実現しており、ある意味極小のアナログコンピュータといえるかもしれません。

SPICEアナログ回路シミュレータ

SPICEとはWindows以前から存在するアナログ回路シミュレータのアプリレーション・ソフトウェアで、MS-DOSではPSpice、UNIXにはHSPICEがありました。Windowsの時代になってもデファクト・スタンダードはPSpiceでしたが、アナログ半導体メーカ旧リニア・テクノロジーからLTspiceが無償提供されるとアマチュアの間でのデファクトになりました。LTspiceは現在でも旧リニア・テクノロジーを買収したアナログ・デバイセズのサイトから無償ダウンロード可能です。

SPICEはデジタル演算でアナログ回路シミュレーションを行いますが、SPICE上で積分器や加算器を組み合わせてアナログコンピュータのように微分方程式をシミュレーションをすることも可能です。 ちょっと倒錯しているかとも思えますが、かなり有効な手法です。 この場合、実際のオペアンプのSPICEモデルは用いず、ゲインを10⁶(120dB)程度に設定した電圧制御電圧源(Voltage Controled Voltage Sorurce)を演算増幅器の代わりに使用します。SPICEモデルとしてのVCVSはゲインを無限大に設定できないことを除いては、入力インピーダンス無限大、出力インピーダンスがゼロ、周波数帯域が無限大の理想オペアンプの条件を満たしています。

このあとアナログ回路シミュレータのLTspice上で感染症SIRモデル微分方程式のシミュレーションに挑戦します。

乗算器をLTspice上で構成

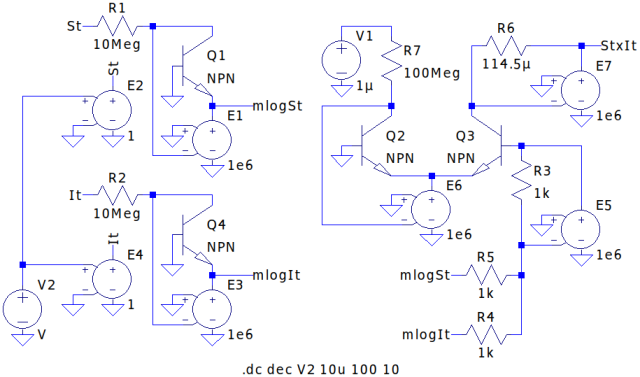
S(t)I(t)の演算のためにLOGアンプ→加算器→アンチLOGアンプの構成で乗算器を作成しました。抵抗値は実際の電気電子回路としてどうなのか?という値になっていますが、広いダイナミックレンジを確保するためのあくまでシミュレータ上の値ということで割り切ります。

• 回路図左側のそれぞれR1,Q1,E1とR2,Q4,E3で構成される回路がLOGアンプで、Q1およびQ4のNPNバイポーラ・トランジスタの $V_{BE}$ と $I_E\left(\fallingdotseq I_C\right)$ が指数関数 $I_{\text{E}}=I_{\text{S}}\left[exp\left(V_{BE}\frac{q}{kT}\right)-1\right]$ であることを利用した回路です。 $I_C\left(\fallingdotseq I_E\right)$ が入力 $V_{BE}$ が出力なので、指数関数の逆関数である対数関数(LOG)の特性になります。
• 回路図右下のR3,R4,R5,E5が次のステージの加算器です。
• 回路図右上のV1,R6,R7,Q2,Q3,E6,E7が乗算器最終ステージのアンチLOGアンプです。LOGアンプ同様NPNバイポーラ・トランジスタQ3の $V_{BE}$ と $I_E\left(\fallingdotseq I_C\right)$ が指数関数であることを利用した回路です。ただしこちらは入力が $V_{BE}$ で、出力が $I_C\left(\fallingdotseq I_E\right)$ なので、指数関数(アンチLOG)特性になります。なおQ2の役割はQ3のリファレンスです。

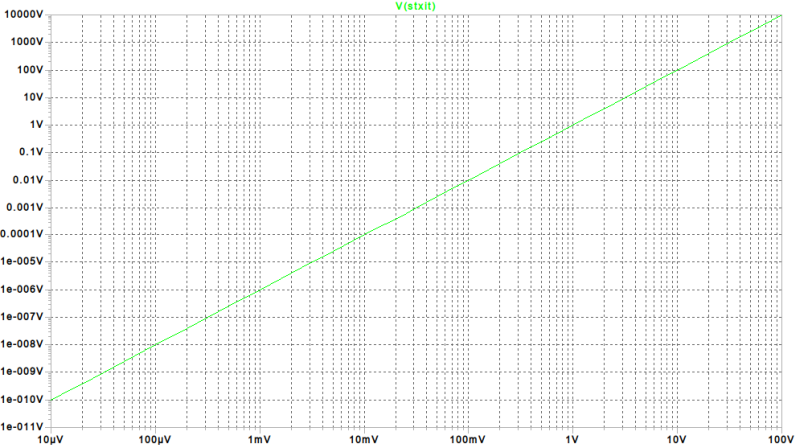
下のグラフは上のシミュレーション回路のDCスイープ出力です。広ダイナミックレンジな二乗特性が得られました。
回路図右上のR6の値はこのグラフをにらみながら入力1V→出力1Vになるようカット＆トライで決定しました。

LTspiceによるSIRモデルシミュレーション

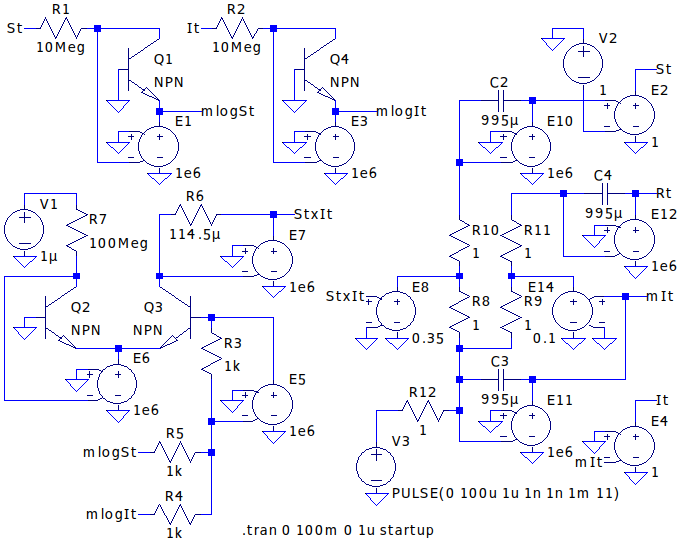
下の回路図はLTspiceによるSIRモデルシミュレーションの全回路です。

• 回路図の左側は前述の乗算器です。
• 回路図の右側はSIRモデルの微分方程式を時間(t)で積分した構成です。タイムスケールをLTspiceで扱い易いよう1day→1msに変換しようと試みましたが、なぜか結果が計算と一致いたしません。原因の究明は半ば諦めて、次善の策として乗算器のR6の定数決めの手法同様、シミュレーションによるカット＆トライで積分器のコンデンサC2,C3,C4の容量を決定しタイムスケール設定しています。(詳細については後述します。)
  初期値 I(t)=0 では常に S(t)I(t)=0 なので感染が始まりません。V3のpulseオプションは感染爆発させるためのトリガ設定です。V2はS(t)のオフセット(=1)を付加するための電源です。
  電圧制御電圧源(VCVS)のE8のゲインがβ、E14のゲインがγに相当します。これらパラメータの値は参考文献^*1を基に設定しています。

下のグラフは上回路でのシミュレーション結果です。V(st),V(it),V(rt) の他に乗算器の動作確認するため、乗算器出力 V(stxst) と StとItそれぞれの出力同士の積 V(st)*V(it) をプロットしていますが、両者のプロットが一致していることで乗算器が正しく動作していることが確認できました。

下のグラフは上のグラフと同じシミュレーション結果を対数軸で表示したものです。
対数軸でも V(stxst) と V(st)*V(it) のプロットは一致しており、乗算器の動作の正しさが追認されました。
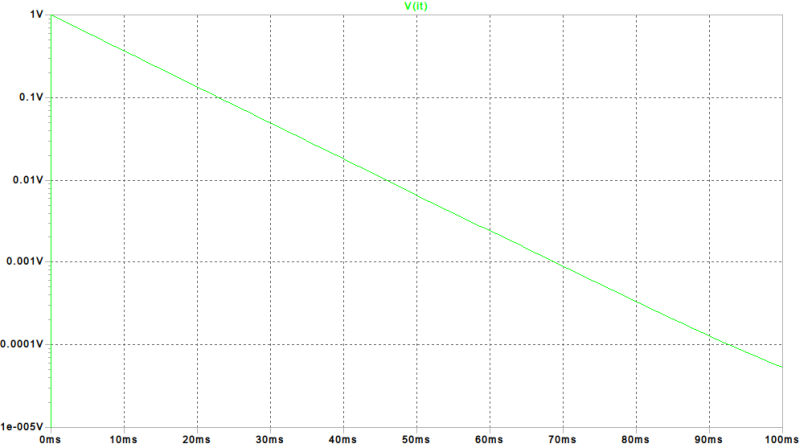
V(it) がピークアウトした後、ほぼ直線的(指数関数的)に減少しています。

ここで V(st) が V(st) << 1 に収束するとき $\gamma -\beta S\left(\mathrm{t}\right)=k$ (=const) , $I\left(\mathrm{t}\right)=y$ とおくと

$\frac{\mathrm{d}y}{\mathrm{d}t}=-ky$

変数分離形の微分方程式として

$\int \frac{\mathrm{d}y}{y}=-k\int \mathrm{d}t$

$\log \left|y\right|=-kt+C_1$

これは$I\left(\mathrm{t}\right)$が片対数グラフにおいて切片$C_1$(積分定数)、傾き$-k$の右肩下がりな直線で表される指数関数

$y=C_2{e}^{-kt}$

に漸近することを示しています。

東京都コロナ第5波PCR陽性者数推移

下のグラフでは東京都のコロナ第5波のPCR陽性者数推移を曜日変動をキャンセルするためにPCR陽性者を7日間の移動平均で対数軸上に表示しています。

9月初めから10月末にかけて、50日間で1/100程度の割合で指数関数的に減少していることが判ります。

ここで $t_1<t_2$ とすると

$\log \left[\frac{I\left(t_1\right)}{I\left(t_2\right)}\right]=-k\left(t_1-t_2\right)$

$\log 100=50k$

$k=\frac{2\log 10}{50}=0.092103$

参考文献^*1の γ = 0.1 という設定値の妥当性が、シミュレーションとこの計算結果からも確認できたのではないでしょうか。

以下、話は遡りますが、シミュレーション回路の積分器のコンデンサC2,C3,C4の容量の設定について説明します。
V(st) が V(st)=0 に収束した場合を考えると $k=\gamma =0.1$ また $\frac{I\left(t_1\right)}{I\left(t_2\right)}=100$ とすると

$k=\frac{2\log 10}{t_2-t_1}=0.1$

$t_2-t_1=\frac{2\log 10}{k}=20\log 10=46.052$

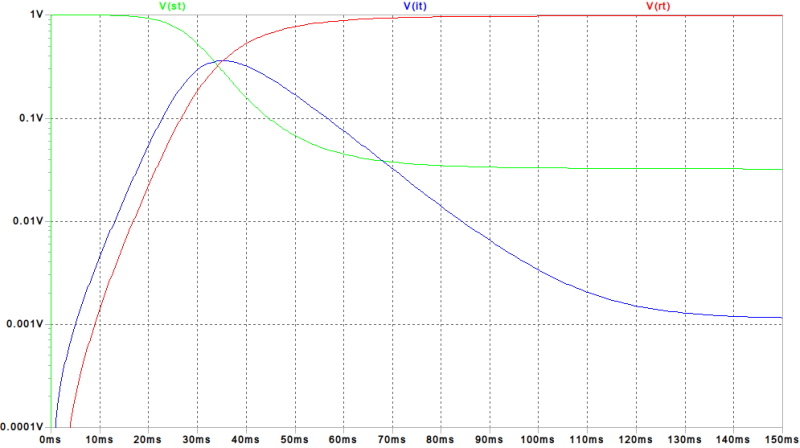
タイムスケール1day→1msとするために、下のシミュレーション回路(γ =0.1)でのフィードバックによるI(t)のステップ応答が、46msで1/100になるようC3の値のカット＆トライを試みました。

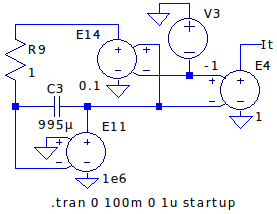
下のシミュレーションのようにカット＆トライの結果、積分器のコンデンサC2,C3,C4の容量を995µFに決めました。

PCR新規陽性者の下げ止まり

東京都のPCR新規陽性者数は10月末までは指数関数的に減少していましたが、11月に入り20数人程度の日が続き下げ止まりとの声が聞かれるようになりました。
下のグラフはLTspiceによるSIRモデルシミュレーション回路のV3の感染爆発トリガのpulseオプションを外し、定常的に100µを入力するように変更したときのシミュレーション結果です。下げ止まりのような結果が現れています。

ここで下げ止まり後も $\beta S\left(\mathrm{t}\right)-\gamma$ が大きく変化していないという仮定のもと、東京都の外(国内外)から一日あたり何人程度の感染者が流入しているかを等比数列という観点から推定してみます。

項比r (0 < r < 1)の等比数列第n項までの和をS_n とすると

$S_n=a_0\frac{1-r^n}{1-r}$
$\underset{n\to \mathrm{\infty }}{\lim }{S}_n=\frac{a_0}{1-r}$

項比は、50日間で1/100に減少することから

$r^{50}=\frac{1}{100}$
$r={\left(\frac{1}{100}\right)}^{\frac{1}{50}}=0.91201$
$\underset{n\to \mathrm{\infty }}{\lim }{S}_n=\frac{a_0}{1-r}=\frac{a_0}{1-0.91201}=11.365a_0$

もしかすると東京都内へ今も感染者が平均2人/日程度流入し続けているのかもしれません。

• JR奈良線第2期複線化竣工
• (PREV)

• Spiceによる感染症数理モデルのシミュレーション