ニュートン力学を見直す　

（2015年10月22日）
　はじめに

　ニュートン力学とはニュートンの運動方程式を中心に関連する法則を展開した一連の理論体系です。振り子の運動やバネと錘の振動など、物体に力を加えた時の運動を解析することなどが力学の応用範囲です。惑星の運動を解析する天体力学、コマの運動など回転体を解析する剛体力学、構造物の強度を解析するために必要な材料力学、などもニュートン力学と深い関係があります。

　ニュートン力学は広い応用範囲を持ち、成功実績も多く、完全に確立した学問であると考えられてきました。ところがアインシュタインにより、特殊および一般相対性理論が提出され、その正しさが認められた現在では、ニュートン力学は相対性理論の特殊な場合に格下げとなり、古典力学と呼ばれるようになってしまいました。

　殆どの工学分野では、古典力学と呼ばれようとニュートン力学で間に合っているから全く変える必要はないと考えている人も多いことでしょう。しかし、アインシュタインはニュートン力学に欠陥を見たのです。ニュートン力学で何も不便を感じない人も、ニュートン力学で間違っているところを知っておくことは何時の日か役に立つことでしょう。あるいはニュートン力学に必要な見直しを加えておいた方が良いのかもしれません。

　１．力

　力と言えば何を思いつくでしょうか。私は力士を思いつきます。二人の力士が土俵上でがっぷり四つに組む状態を思い浮かべてください。二人の力が均衡していると、どちらも力を出しているのに動きません。どちらかが力を抜くとその力士は相手に一方的に押し出されてしまいます。相手に力を加えるということは手や胸で相手を押すということです。

　物体に力を加えるということの基本的な動作は押すこと、つまり圧縮です。相手のまわしを取って引くこともあるし、綱引きなら引っ張るだけではないかとお思いでしょう。しかし、綱を持つ手に油を付けたら手が滑って綱を引くことはできません。綱を引くためには綱と手の間で摩擦が必要なことが判ります。摩擦の働いている部分を拡大して見ることが出来たら、きっと分子間で押し合っているに違いありません。話を簡単にすすめるため、摩擦の力の掛かり方は後回しにしましょう。

　綱を引っ張って力を入れている典型的なスポーツであるハンマー投げを見てみましょう。室伏選手は約85 ｍの記録を出しています。これだけの記録を出すとき、手を離す直前でハンマーに掛る遠心力を計算してみると4000 N （400 kg・重）もの力になります。室伏選手はこのように大きな力でハンマーを引っ張っていることになります。

　ハンマーのワイヤを見てみると、両手で握る握りの部分を介して手の平から圧縮力としてワイヤに力が伝わり、その力がワイヤの内部で引き張り力に変わっていることが判ります。

　
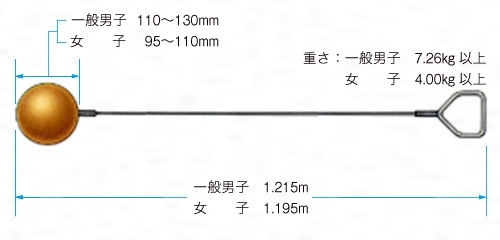
注）右の図で”重さ”とあるのは”質量”が正しい

　力が物体に作用するとき、面を通して伝わることができます。室伏選手がワイヤに力を伝えるときは手の平でした。力は点や線で伝えることは出来ないのです。

　力を点で釣り合わせることが出来ないことは、2本の千枚通しの尖った先を突き合わせてみれば判ります。2本の千枚通しに力を入れることはできません。同じく力を線で釣り合わせることも出来ないことは、2本の包丁の刃を突き合わせてみれば判ります。両手の包丁を持つ手に力は入りません。

　

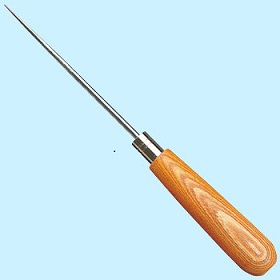
　弓矢を考えてみましょう。矢は弓の弦に押されて飛び出すのです。力は矢印で描かれることが多いのですがその矢は矢筈の部分を弦により押されています。矢筈に弦が当たる面積は小さいのですが、その部分を拡大して見れば面で押されていることが判ります。決して点や線で押されているのではないのです。面で押す力は圧力と言います。力は圧力としてのみ、物体に伝えることができるのです。

　今まで見てきたように、力は一点に集中させることは出来ません。しかし、これに反する簡素化をするのが質点系力学です。質点系力学では物体の質量は1点に集中しているとみなします。そして、力も1点に作用すると考えるのです。このように単純化する一番のメリットは力をベクトルで表すことが出来ることです。

　ベクトルは大きさと方向を持った量です。力がベクトルで表されると、多くの力がいろいろな方向からかかった時の運動などをベクトル計算で簡単に解析できるのです。ロケットの飛行解析から惑星の運動まで多くの事柄が質点系力学で間に合います。

　多くの力学の教科書が最初にベクトルの算法から始めていることもあって、力はベクトルであると信じている人も多いことでしょう。しかし、力をベクトルで表示することは近似であることを忘れてはいけません。それではベクトルで表すことで何が拙いのでしょうか。

　物体が静止しているとき、二つ以上の力が働いてそれらが釣り合っているから静止しているのか、力が全く作用していないから静止しているのかの区別がつかないということがあります。

　それでは力はどういう時に発生しているのでしょうか。力は目に見えるものではありませんから力が加わった物体の状況を見るほかはありません。二人の力士が土俵上で組み合って動かないときは、お互いの表情や筋肉の盛り上がり方で相互に力を出し合って均衡しているのだと判ります。物体に外から加える力という意味で外力と言う言葉があります。この二人の力士は外力と外力の釣り合い状況なのです。

　「暖簾に腕押し糠に釘」という諺があります。これは相手がしっかりしていないと力が入らないという譬えです。言い換えると力が作用しているときは、常に力が釣り合った状態にあるということです。

　ここで、ちょっと待った異論があると思われる方も多いでしょう。ロケットは推力を出していて釣り合っていないから飛んでいくのではないかと。まさにその通りです。物体に力が加わると加速度を生じて物体の運動が変化します。

　ニュートンは有名なプリンピキアで物体に力が加わったとき物体の運動量の時間変化が力であるという記述をしています。後世の人がこの関係から力は物体の質量に加速度を乗じたものに等しいと書き変えています。質量をｍ、力をＦ、加速度をαとして記号で表すと、Ｆ＝ｍαという式で表されます。この式がニュートンの運動方程式と呼ばれるものです。ニュートン力学で最も重要な式と言っていいでしょう。
　
　ロケットに戻って考えます。ロケットの推力がＦでロケットの質量がｍであると、ロケットは加速度αの運動をしている訳です。ロケットは一方的に力Ｆを受けているから加速度を伴う運動をしているのですが、ロケットのエンジンは後部についていますので、ロケット自体は圧縮力を受けた状態です。加速度に質量を乗じた量、ｍα、を慣性力と名付けるとロケットの推力Ｆは慣性力と釣り合っているとみなすことができるのです。これはダランベールの原理と呼ばれます。

　この慣性力を”見かけの力”と呼ぶ人もいます。この場合の”みかけの”という意味は外力でないという意味でしょう。しかし、”みかけの”という言葉は本当は違うがという意味ですから適切ではありません。推力（又は外力）Ｆに釣り合っている慣性力は実際の力だからロケット内部に圧縮力を生じているのです。

　二つの外力が釣り合っている場合は一つの外力が慣性力と釣り合っている状態に、反対向きの外力が慣性力と釣り合っている状態が同時に重なっているものと見なすことが出来ます。このように考えれば、外力と外力が釣り合って静止している物体内部には圧縮応力が生じていることも説明できます。力が掛っていないので静止している物体には圧縮応力の発生はありません。

　つまり物体に作用する力は慣性力と釣り合うこと、Ｆ＝ｍα が基本的なことなのです。面で作用した力は質量に由来する慣性力と釣り合うのですから、慣性力は体積力であると言うことが出来ます。

　そろそろ力とは何かの定義をしましょう。意外なことに多くの教科書で力の定義を敢えて載せることはしていないようなのです。私の手元にある次の2冊の力学の教科書には載っていません。
　岩波基礎工学「力学Ⅰ」小野周著、
　「力学」戸田盛和著、岩波書店

　それならば辞書で見てみましょう。ブログ「力とは何か」に大辞林を引用してあります。これに見るように物理用語としての力には二つの要素があると書かれています。

　一つ目は、物体に力が作用すると加速度運動を生じるということです。二つ目は力が作用した物体には応力・歪を生じているということです。辞書にはこの二つの要件を満たしたものが力なのか、どちらか一つでも力というのかが明確ではありません。質点系力学では応力・歪を考えなくて良いのですから、物体に作用すると加速度運動を生じるだけになります。
　
　ニュートン力学での最初の欠陥は力の定義が明確でないことです。ここで力の定義を次のように明確にしておきましょう。
　　*　力とは物体に作用したときその物体に加速度運動を生じ、かつ、その物体内部に応力・ひずみを生じる。　*

　ここで、少し困ったことがおきます。物理学では自然界に四つの力が存在すると言います。このときの四つの力とは、重力、電磁気力、強い力、弱い力ですが、上述の力の定義には当てはまりません。物理学者も人によっては四つの力と言わずに四つの相互作用と言うのも力の定義に不足を感じるからでしょう。内容さえ正しく掴んでしまえば用語の適切さは気にならなくなることは確かですが、他人に説明するときには常に適切な用語が望まれます。

　力の元をたどると、分子と分子の反発力ですから大部分が電磁気力相互作用であると考えられます。もう一つは慣性力ですから、慣性力の元をたどると質量の性質である慣性ということになります。重力は次の章で詳しく検討しますが、重力は力でないのです。強い力と弱い力は原子核内部の相互作用ですから応力・ひずみの概念は全くありません。

　力の定義は上述の2要素で良いと思われますが、力の性質というものも見ておく必要があります。力は直接には目に見えません。においもありません。味もしません。音もありません。従って、人間の５感で直接関係するのは触覚だけです。

　力は物体を通じて伝わりますから、力の伝わる速さはその物体内部を伝わる音速に等しいのです。これは意外と思う方も大いでしょう。万有引力や重力は光速で伝わるのでないかと思われる方もおいででしょう。万有引力はニュートンが示したものですが、実際にはこのような力は存在しないのです。詳細は次の章で説明します。また重力波は光速で伝わると考えられていますが、重力と言う力が光速で伝わるのではないのです。

　ニュートンは万有引力の作用は遠隔力であることを嫌ってはいましたが、実際の力と考えたため瞬時に伝わる遠隔力と考えざるを得なかったのです。しかし、力は遠隔力で伝わるのではありません。常に分子間に働く電磁気相互作用の結果として伝わるものです。

　２．重力

　地球上の物体は殆どのものが地上に向かって落ちていきます。空を飛ぶ鳥も羽ばたくことを止めれば地上に落ちます。煙やヘリウムガスを詰めた風船のように上に向かっていくものもあります。アルキメデスの時代では地上に落ちていくもの、上に向かっていくもの、それぞれの物体の性質で行先が決まっていると考えられていました。

　結局それらも空気との比重の差の問題であって、全ての物体は地上に向かって落ちていく性質があることが判りました。物体が地上に落ちていくのは重力（Gravity）の作用であると考えられるようになりました。ガリレオは斜面を利用して地上に落ちていく物体の加速度が一定であることを発見しました。

　ガリレオがピサの斜塔から比重の異なる同じ大きさのボールを落として、同時に地上に着くことを確かめたという有名な実験があります。さすがにこの話は後世の人の作り話のようですが、全ての物体に働く重力加速度がどの物体に対しても一定であることを発見したのは大きな業績です。

　重力が力であると考えられるようになったのはニュートン以後のことです。現代でも最先端の物理学者を除いて、一般的にはそのように考えられていて、国土地理院のHPでも地球の重力は万有引力と地球の自転による遠心力との和であると定義されています。星の運動など自転を考えなくて良い場合は重力は万有引力と同じとして構いません。

　チコ・ブラーエが収集した正確な惑星の運行データをもとに、ケプラーは惑星の運動はケプラーの３法則と呼ばれる法則を打ち立てました。すべての惑星は太陽を中心とする円運動ではなく、太陽を焦点とする楕円運動をしていることを明らかにしたものです。ケプラーの３法則で日食や月食の予報が正確に出来ることからも、直ちにその法則の正しさは認められました。

　ハレー彗星に名を残すエドモンド・ハレーはケプラーの法則が成立する理由をニュートンに聞いたのです。どうして星の運動はケプラーの３法則で規定されているのだろうかと。この質問を受けて、ニュートンは重力が働いているからだと答え、有名な万有引力の式を示したのです。確かに、万有引力の式からケプラーの３法則は導くことが出来たのです。

　これがニュートンを最も有名にした万有引力の法則です。しかし、ニュートンはどのように万有引力の式を思いついたのでしょうか。ニュートンが意識していたかどうかは判りませんが、万有引力の式から三つの法則が導ける、という提示の仕方が非常に効果的だったに違いありません。三つの法則を規定する一つの法則なら、その一つの方がより基礎的な上位の法則であるとの印象があります。

　ニュートンもケプラーの３法則から万有引力の式を導いたに違いありません。ニュートンがケプラーの３法則から万有引力の式が導けるという示し方をしたのなら、ニュートンよりケプラーの名声が残ったかも知れません。ケプラーが３番目の法則を見つけたときに非常に喜んだのは判ります。しかし、それで満足せずにもう一歩考えを進めていればニュートンの万有引力の法則もケプラーのものになった筈です。もし、そうしていれば自然界には万有重力加速度が存在するということになったかも知れません。

　ケプラーの法則からニュートンの万有引力の法則を導く方法は湯川秀樹の「理論物理学講話」に紹介されています。ケプラーの法則から逆二乗則である重力加速度の式が導けるのです。湯川秀樹もこの本では気がついていないようですが、加速度があれば力が働いている筈だとしています。逆は必ずしも真でないのですが、何の疑いもなくニュートンの運動方程式を利用して加速度を力と質量の比に置き換えています。これによりニュートンの万有引力の法則は次元が力の式になっています。殆どの力学の教科書で天下りに万有引力の式が示されています。万有引力の導出は載っていません。ニュートンがひらめきで提示したかのようです。

　力の定義で物体に力が働けばその物体は加速度運動を始めるということでしたが、加速度運動があっても必ずしも力が働いているとは言えなかったのです。ケプラーの法則から演繹的に導き出されることは二つの物体間には加速度運動があるということだけなのです。ニュートンは万有引力という仮説を提示したつもりでないならば、ニュートンの早合点ということになります。

　万有引力は星の運動を説明するし完全に証明されているではないかと思われる方も多いでしょう。しかし、いくら運動を説明できても力であることの証明にはなりません。そうです、物体に働く力はその物体に加速度運動を起こすだけでなく、その物体に応力・歪を発生させるものでなければなりません。ニュートンの万有引力は物体に運動を起こすだけでその物体内部に応力・ひずみを発生させていないのです。次元が力であることには変わりありませんので、「みかけの力」であるといわざるを得ないでしょう。

　まだ、納得がいかない人もいます。ニュートンが間違うはずがないし、300年前から確立していることだから無理もありません。力の定義を少し変えてみることにしましょう。力とは物体に作用すると加速度運動を生じるだけにするのです。そして、力の性質として物体に外部から面を通して外力として作用すると物体内部に応力・歪を生じるとするのです。

　このように力の定義を簡単にするとフックの法則を基礎とする材料力学も力の性質を利用した学問という位置づけになるだけで何も問題は無いように見えます。加速度に質量を乗じたらそれは力であるとするならば、万有引力も重力も力ということになります。

　実際に現状はそうなのです。しかし、力に2種類あることになります。物体に作用してその物体内部に応力・ひずみの発生を伴う力と伴わない力です。前者は外力と呼ばれます。後者は数式上は力の次元ですが実在を検知できない力です。外部から運動を観測すれば判ると思われても運動は観測する座標に依存します。これは見かけの力と言わざるを得ません。

　重力は力であるとするにしても、無重力状態の説明を考えると見かけの力でしかないことが結論できます。

　高いところから飛び降りた時、ふわっとする感じがあります。もし空気抵抗がなければ地上に向かって真っすぐに落ちていきますが、この間は何も力を受けていないような感じになります。しかし、重力という力を受けているのですから、それは慣性力と釣り合っているからそうなるのだという説明です。

　地球を回る宇宙ステーションも常に地球に向かって落下しています。ただ、その水平速度が速いことと、地球が丸いこと、により何時までも地表に達しないのです。宇宙ステーションの中でも無重力状態になっているのは重力と遠心力（慣性力）が釣り合っているからだという説明にせざるを得ません。

　今でも無重力状態の説明は重力と慣性力が釣り合っているからだという説明の本が多いのです。しかし、この説明では次の矛盾が解決できません。

　もし、宇宙ステーションがどの星からも遠く離れた宇宙空間にあったとしたら、重力も何も働いていませんからやはり無重力状態です。この状態と、地球周辺を周回しているときの宇宙ステーションとの区別がつかないのです。重力と慣性力の釣り合い状態にあるのか、力が全く作用していない状態なのかの区別がつかないのです。

　二つのものの違いが判る方法が全く無い時は同じとするのが等価原理です。宇宙ステーションが飛行する高度は約400ｋｍですから、重力の大きさは地表面の89％もあります。地球を周回しているときは重力と慣性力が釣り合っている状態と全く重力が無い空間にいる状態と区別がつかないのです。重力を力であるとすると矛盾が生じる（等価原理に反する）ということです。

　このことに最初に気がついたのがアインシュタインで1907年のことであったそうです。自由落下をしている物体に重力が消えているということに気がついたという表現でした。重力が力でないことに気がついたと話していれば無重力状態の間違った説明が残ることはなかったかもしれません。多くの人は重力と慣性力が釣り合っていることを重力が消えていると表現しただけと捕えたのではないでしょうか。彼は、この発見に力を得て自分の考えを表現するために難解な数学にも取組み、その結果1916年に一般相対性理論を確立したのです。

　重力が力でない証拠はあります。殆どの加速度計はバネと錘でモデル化できるものです。このような加速度計で重力加速度は計れないのです。その理由は、これらの加速度計は力を検知して加速度に換算するものだからです。ロケットに加速度計を搭載して実際の飛行データが基準軌道に合っているか比較しながらエンジンの推力と方向を制御していますが、重力だけは実測できないので計算値を使います。

　重力に従って自由落下していてもその重力により無重力状態になるのは局所的だから、星から十分離れて全く力が加わっていない状態と自由落下による無重力状態とは少なくとも理論的には区別できると反論される方もいます。重力は1点に向いた作用ですから、大きな物体はその物体を構成する全ての分子が拘束なく自由落下することは出来ないのです。落ちる方向には引き張り力、水平方向には圧縮力が発生します。これを潮汐力と呼んでいます。

　確かに、大きな物体では重力による潮汐効果は無視できません。しかし、この潮汐力は重力加速度に質量を乗じた値に比べれば通常の大きさの物体では無視できるほど小さいものです。地球を周回する国際宇宙ステーション（ISS）の大きさで、潮汐力を実測できるものではありません。

　どの星からも十分離れた宇宙空間でない限り何処にいても重力の影響下にあります。具体的には太陽系のどこにいても大洋の重力の影響下にあります。地球近辺では地球の重力が太陽や月の重力よりも大きいだけです。重力の影響下にある空間は重力場と言います。

　ニュートンの運動の法則は重力場ではどう書き換えられるのでしょうか。慣性の法則は次章で説明しますが全く表現が異なってきます。ニュートンの運動方程式も重力場の運動方程式に置き換える必要があります。作用反作用の法則はそのままでも良いでしょう。慣性の法則も、作用反作用の法則も重力場の運動方程式に含まれている法則です。

　
　３．　慣性

　全ての物体が例外なく有する特性として質量があります。素粒子のレベルですと質量のない光子があります。ニュートリノは質量がないと考えられてきましたが最近になって質量のあることが実証されました。

　質量を特徴づける性質は慣性です。慣性とは運動変化に抵抗する性質です。ニュートンの運動の第一法則は慣性の法則とも呼ばれています。物体に何も力が働かないときに静止している物体は静止のままで、運動している物体は等速直線運動を続けるというものです。

　この慣性の法則は修正する必要があります。地球の周辺に限らず、宇宙空間ではすべて重力の影響にあります。重力は力でありませんから、物体に何も力が働かないときその物体は重力に従った運動、還元すると自由落下運動、をしています。自由落下運動は等速でもないし、重力に垂直方向の速度成分を持っていれば直線運動でもありません。

　自然界に存在する四つの力の内、重力は力でないとすると三つの力になってしまうのでしょうか。そうではありません。力の章でも出てきましたように、重力の代わりに慣性力が置き換わります。慣性力は外力に抗する力ですから受動的な力です。そして慣性力は質量に比例しますから体積力でもあります。
　
　
　

　４．まとめ

　ニュートン力学で直すべきところはどこでしょうか。簡単にまとめてみます。

①　力の定義を明確に定める。力とは物体に作用したとき、その物体に加速度運動を生じさせるとともに応力・ひずみを生じさせる。

②　質点系力学での力は近似であることを明記する。

③　力は面で作用し、常に慣性力と釣り合う。慣性力は質量の性質である慣性に基づく体積力である。

④　力が伝わる速さは音速である。

⑤　重さは力で単位は［N］。質量の単位［kg］と混同しないこと。
　　（理科の教科書では既に徹底されています。）

⑥　ニュートンの万有引力は見かけの力であって、力として実在するものではない。

⑦　ニュートンの運動方程式は重力場の運動方程式で置き換える。

⑧　ニュートンの運動の第一法則（慣性の法則）は重力場の慣性の法則に置き換える。

⑨　重力は力でないことを認識する。
　　（重力場が質量に与える作用は力としてではなく加速度運動としてである。）

（了）

戻る