|
(作成:2011年11月25日
修文:2015年2月25日)
ニュートンが万有引力の式をケプラーの法則から導き出した骨子を示す。
ニュートンの運動の第2法則は運動方程式とも呼ばれる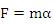 もニュートンがプリンシピアに記した表現は もニュートンがプリンシピアに記した表現は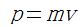 を運動量として を運動量として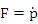 であり、しかも数式でなく文章である。ニュートン自身は であり、しかも数式でなく文章である。ニュートン自身は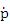 が が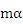 のことだと言ったのかどうかは判らないが、万有引力の導出において のことだと言ったのかどうかは判らないが、万有引力の導出において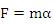 が使われている。 が使われている。
ケプラーはチコ・ブラーエが集積した惑星の観測データを使って次の3つの法則を打ち立てた。
(1)
惑星の運動は太陽を一つの焦点とする楕円軌道である
(2) この楕円軌道を掃引するときの面積速度は一定である
(3) 惑星の周期Tの2乗は軌道の長径aの3乗に比例する
式を簡単にするため、火星は楕円軌道でなく半径 r
の円軌道で太陽の周囲を回っているものとする。火星の位置を極座標表示の 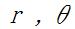 で表すと、火星の速度は で表すと、火星の速度は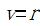 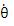 である。火星が円運動をしているということは、火星が円周の接線方向にvの速度で運動していると同時に太陽方向に加速度 である。火星が円運動をしているということは、火星が円周の接線方向にvの速度で運動していると同時に太陽方向に加速度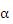 = =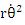 で運動しているということである。 で運動しているということである。
ケプラーの第(3)法則から、Kを定数、Tを周期として、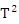 =K・ =K・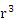 である。 である。
一方、T=2πr/v=2π/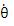
故に、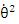 = =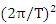 = =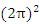 /(K・ /(K・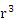 ) )
これらから、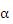 ={r ={r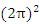 /K}/ /K}/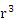 =定数/ =定数/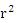 となる。 となる。
以上が重力加速度が距離の逆2乗則になる証明の骨子である。
ニュートンのプリンピキアでは幾何学的に導かれており、少し難解であるが結論は同じである。
ケプラーの法則から、演繹的に導かれたのは、重力加速度が距離の二乗に逆比例するという事実である。逆に言えば、重力加速度が距離の二乗に逆比例するという結論は星の運動を観察することにより実証されているということである。
定数の次元は[m^3/s^2]である。
ニュートンはこの定数は太陽の質量Mに比例するに違いないと考えた。この点はニュートンの明察うりを示している。そこで定数=GMとした。Gの次元は[m^3/(s^2・Kg)]となってしまうが、太陽のMの場合も地球のMの場合もGは一定であることを発見したのである。Gはニュートンの万有引力定数と名付けられている。万有の名に値する普遍的な定数だったのである。
さらにニュートンは運動の第2法則から、加速度は力を質量で除したものであるから、F/m=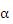 =定数/ =定数/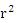 であるとした。
F/m=GM/ であるとした。
F/m=GM/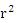 となり、rをRと書き直すと有名な万有引力の式が得られる。 となり、rをRと書き直すと有名な万有引力の式が得られる。
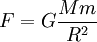
ニュートンの早合点は、加速度があれば力が作用しているとして考えたところにある。万有引力の式は力の次元の式になっているが、あくまでも仮説に過ぎない。
チコ・ブラーエの観測データは位置と時間情報であるから、追加の仮定なしに導かれる次元の物理量は加速度までである。つまり天体観測によるデータをいくら集積しても、運動の観察でしかないから万有引力が力として作用していることの実証にはならないのである。
キャベンディッシュの実験では万有引力を力として検知したように見えるが、実際は加速度運動を止めるに必要な力を検出したものである。地球の重力を重さとして検知しても、加速度運動を停止させる力を検出しているのであって、重力が力であることを検知したのではないのと同じである。
さらに、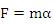 の式で表される質量mを慣性質量というのであるから、少なくとも式の導出からみても万有引力の式のmは慣性質量である。それではMはどうかという疑問は残る。しかし、2連星を想定すればmとMは立場が同じであることが判る。従って、Mを重力質量と区別する理由はない。この点でも、何故アインシュタインの時代まで、そして今でも多数の教科書において慣性質量と重力質量と二つの概念を記しているのか解せないことである。 の式で表される質量mを慣性質量というのであるから、少なくとも式の導出からみても万有引力の式のmは慣性質量である。それではMはどうかという疑問は残る。しかし、2連星を想定すればmとMは立場が同じであることが判る。従って、Mを重力質量と区別する理由はない。この点でも、何故アインシュタインの時代まで、そして今でも多数の教科書において慣性質量と重力質量と二つの概念を記しているのか解せないことである。
GMの値は10桁以上の精度で求められているが、GとM単独の値に対しては精度が4,5桁程度でしか求まっていないのは上述の導出経緯からも納得できることである。
参考:別冊「数理科学」サイエンス社、『力とは何か』、力の本質を秘める逆2乗則、荒木不二洋、1995年4月
(了)
戻る
|