重力場の運動方程式　 

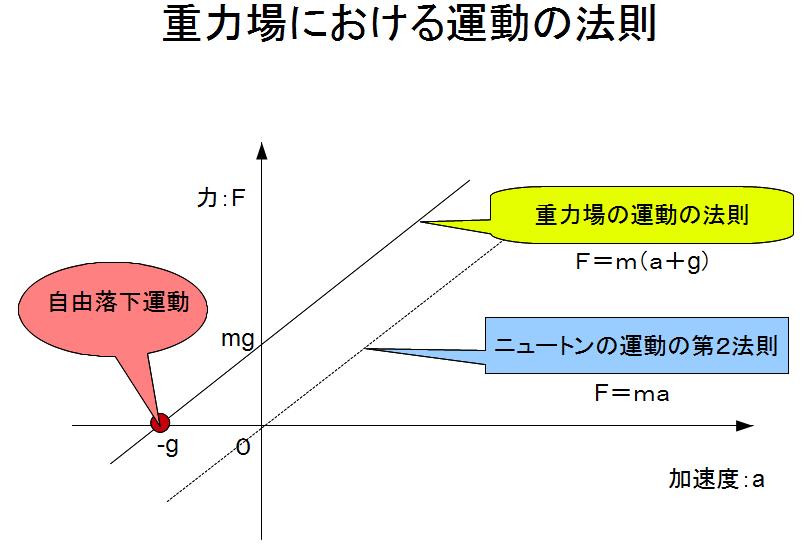
（2011年2月8日） (6月2日改訂）  　ニュートンの運動の第２法則は運動方程式とも呼ばれる。力は質量と加速度の積であるという式である。しかし、この式が成立するのは重力が働いていない空間に限られる。地球の周辺には至る所で重力が働いている。ニュートンの運動方程式が成立するのは、実は重力に直交する方向のみだったのである。 　地球を周回している宇宙ステーションは地球の重力に対して自由落下している。従って、宇宙ステーション内では重力が働いていない、無重力状態にある。つまり、宇宙ステーションに固定した座標系では重力が消されているので、宇宙ステーション内ではニュートンの運動の法則が成立する。 　これまでは重力を外力の一種とみてニュートンの運動方程式を使ってきた。重力加速度に質量を乗じて、万有引力という力が働いていると考えられていたからである。このように考えても実質的な不都合がなかっただけのことである。 　下の図は横軸に加速度、縦軸に力を取った運動方程式のグラフである。ニュートンの運動方程式は原点を通っているが、重力場でのニュートンの運動方程式は−ｇだけ左に移動させたものとなる。つまり、重力を考えたときのニュートンの運動法則から、勾配の質量ｍは慣性質量であり、重力質量の概念が不要である。 　この図からも、物体を地上に静止させるということは加速度がゼロの状態にするということなので、力Ｆ＝ｍｇが必要なことがわかる。また、力を加えないときはＦ＝０なので、加速度が−ｇで運動することがわかる。この運動が自由落下運動なのである。   　　 　重力場では加速度ａで物体を動かすために力Fが必要である。この力Fの大きさは慣性力ｍ（ａ＋ｇ）に等しい。これまでは、重力場においては慣性力ｍｇに等しい大きさの重力と称する力が加わるので、F-mg＝ｍａと説明されてきた。数式上は同じに見えるが、運動の第２法則はａ＝(F/m）とするほうが物理に忠実であり、重力場ではa＝（F/m) - gである。 　地上に静止している物体は加速度ａ＝０であり、このとき地上から慣性力ｍｇに等しい力Ｆの反力を受けている。この場合、実際の力Fに釣り合う慣性力mgも実際の力である。自由落下運動中はF=０であり、ａ＝ーｇとなるが、このとき質量mを乗じたmgという量は見かけの力である。 戻る