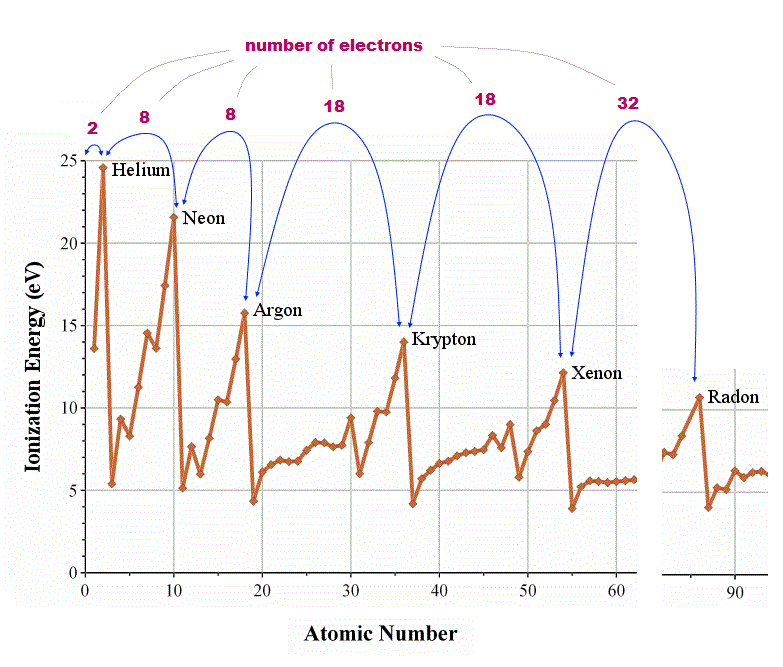
(Fig.1) ↓ Periodicity of ionization energies shows true valence electron number

How can we know how many valence (= outer ) electrons each atom has ? We should look at the periodicity of the first ionization energies of atoms.
In atoms just after noble (= inert ) gases, ionization energies suddenly drop, which indicates their electrons enter outer new different orbitals.
From this change, we can know true numbers of valence electrons in each atom ( He = 2, Ne, Ar = 8, Kr, Xe = 18, Rn = 32 electrons ).
(Fig.2) 4d and 3s, 6s and 4f orbitals are reversed in quantum mechanics !?
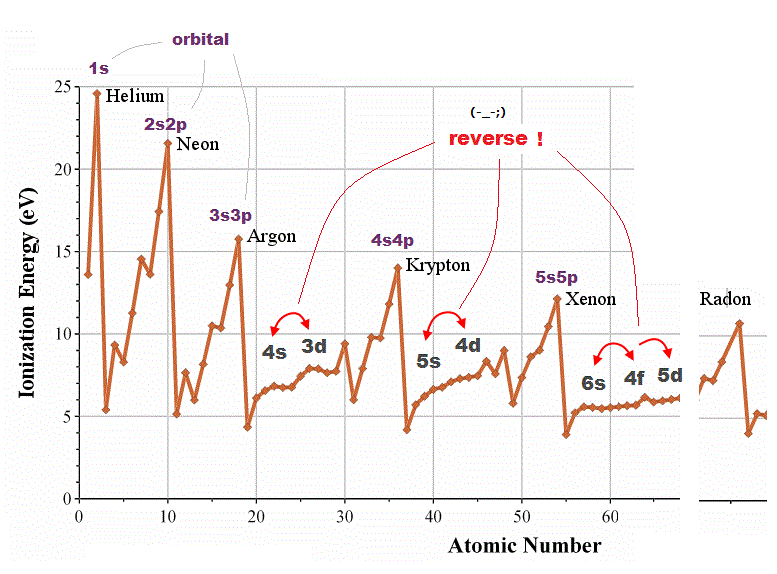
Quantum mechanical orbital are self-contradictory in periodic table. In one-electron hydrogen atom, energy levels are higher in larger quantum number ( 3s < 4d < 4f < 5d < 6s ).
But in other multi-electron atoms, their orders are reversed ( 4s < 3d, 6s < 4f < 5d ) ! Schrodinger equation has NO ablity to predict energy levels in multi-electron atoms.
They just choose fake trial functions giving their desired artificial values. So meaningless and useless.
For example, though magnesium and singly-ionized alminum have exactly the same valence electrons, their orbital orders are chaotic.
(Fig.3) Maximum numbers of orbits in noble gases
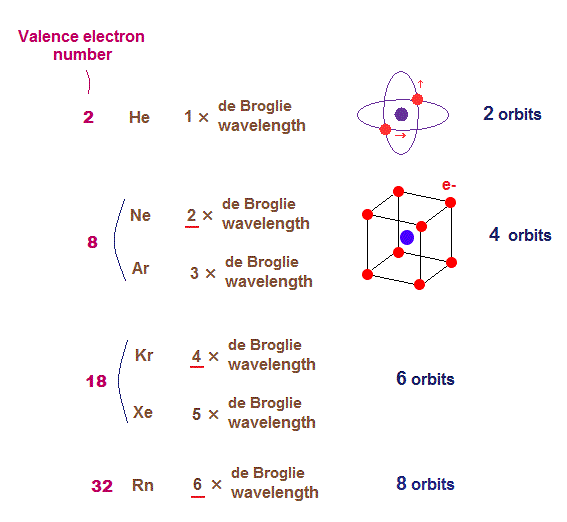
As shown on this page, de Broglie wavelength influences the number of maximum orbital number in the periodic table.
The maxium number of orbits in Ne with 2 × de Broglie wavelength becomes "4" (= each 2 electrons × 4 orbits = 8 valence electrons ).
Krypton (= Kr ) with 4 × de Broglie wavelength has the maximum "6" orbits. Radon (= Rn ) with 6 × de Broglie wavelength has the maximum "8" orbits.
The odd numbers of "3", "5", "7" orbits are asymmetrical and unstable.
So the orbital numbers of "Ar" (= 3 × waveslength ), "Xe" (= 5 × waveslength ) remain the same as "Ne" and "Kr".
(Fig.4) Quantum orbit satisfies an integer times de Broglie wavelength.
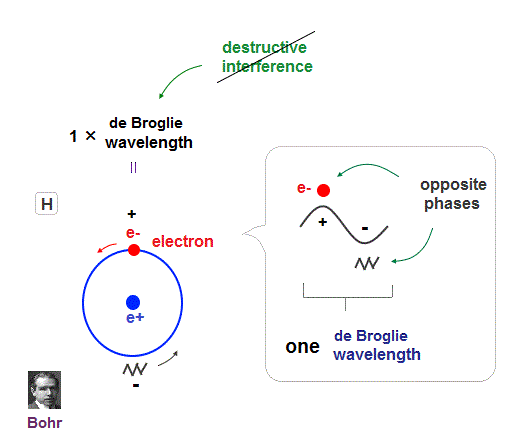
Only Coulomb force is insufficient to explain why atomic energy levels are quantized, and why an electron doesn't fall into nucleus.
Bohr model succeeded in getting actual atomic energies, proposing each orbit is an integer times de Broglie wavelength, as well as Schrodinger's hydrogen .
An integer multiple of de Broglie wavelength means an electron can avoid destructive interference and be stable.
Without this de Broglie wave, each electron can be attracted to positive nuclei, until they stick to each other and its energy is unlimitedly lower !
So the repulsive force by electron's de Broglie wave is strong enough to keep the electron away from the nucleus and cause Pauli exclusion force.
(Fig.5) Opposite phases of two de Broglie waves cancel each other

In old Bohr's helium, two electrons are moving on the opposite sides of the nucleus in the same circular orbit (= one de Broglie wavelength ).
Considering Davisson-Germer interference experiment, two electrons of old Bohr's helium are clearly unstable.
1-de Broglie wavelength orbit consists of a pair of the opposite wave phases (= ±ψ ), which cancel each other by destructive interference.
Due to Coulomb repulsion between two electrons, one is always on the opposite side of another where the opposite de Broglie wave phases cancel each other.
Actually, old Bohr's helium of Fig.5 gives wrong ground state energy of helium, when you calculate it.
Old helium gives the total energy of -83.33 eV, which is a little lower than the actual value of -79.005 eV (= 1st + 2nd ionization energy of this ).
(Fig.6) Actual Helium must avoid "destructive interference".
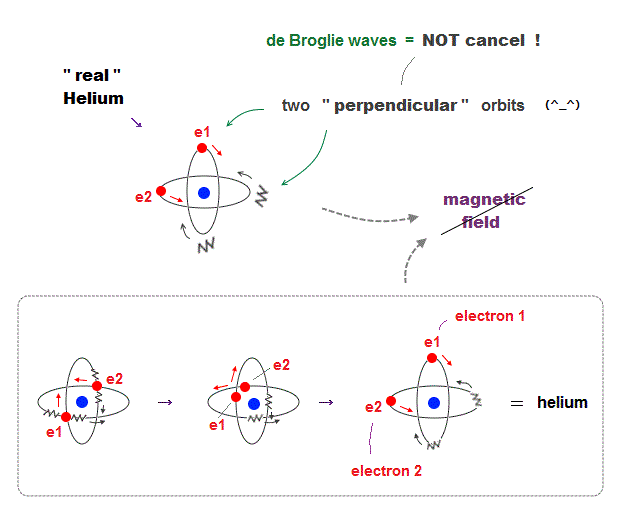
If two 1 × de Broglie wavelength orbits are in the same plane in old Bohr's helium model, their opposite wave phases cause destructive interference and vanish.
To avoid vanishing de Broglie's wave, two electron orbits in actual helium must be perpendicular to each other. Each orbit is one-de Broglie wavelength.
If the two orbits are perpendicular to each other, their wave phases are independent from each other and can be stable, not canceling each other.
This helium model considering actual de Broglie wave interference just agrees with experimental results of all atoms !
(Fig.7) 2 × de Broglie wavelength orbits. Each is a pair of opposite phases.
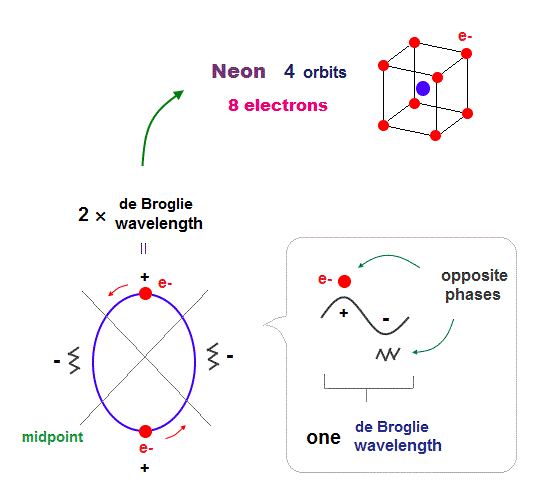
One wavelength consists of a pair of "crest" (= + ) and "trough" (= - ) irrespective of transverse and longitudinal waves.
Here we suppose "+" phase contains an electron itself, and "-" phase is compressed by the electron's movement, --- which is " de Broglie wave ".
2 × ( 1 × ) de Broglie wavelength orbit contains two ( one ) pairs of ±opposite phases and two ( one ) midpoint lines.
These "opposite" wave phases cancel each other by destructive interference.
To avoid it, two orbits must cross perpendicularly in all atoms.
(Fig.8) All opposite wave phases just cross each other in Neon
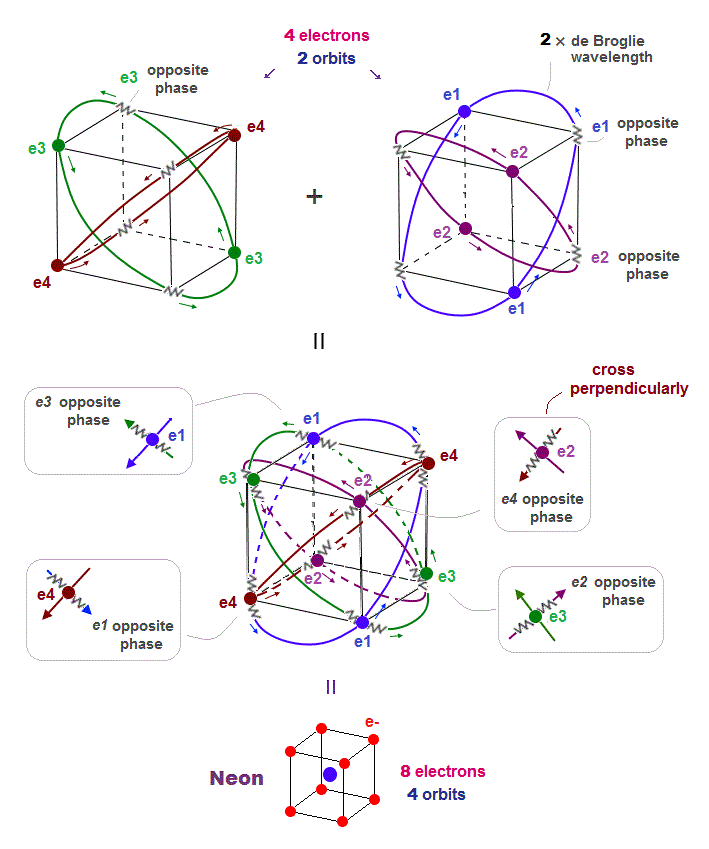
Neon contains eight valence electrons. Neon belongs to the 2nd line in periodic table, meaning its orbit is 2 × de Broglie wavelength.
When just two 2 × de Broglie wavelenght orbits cross each other (= Fig.8 upper ), some electrons are free from their opposite wave phases.
With four orbits, all electrons and their opposite wave phases cross each other, forming stable noble gas Neon with no more room.
(Fig.9) Each orbit contains 2 electrons and "1 hole" in Argon
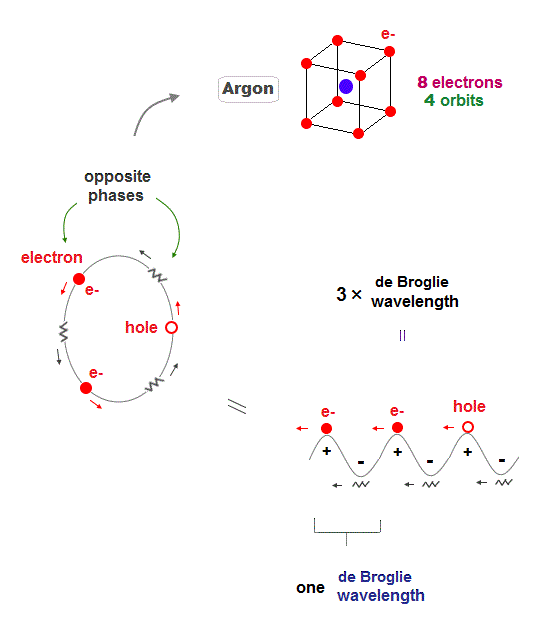
Argon (= Ar ) has 3 × de Broglie wavelength orbits which can contain up to 3 electrons. But Argon has 8 valence (= outer ) electrons.
It means each orbit of Argon contains 2 electrons and 1 hole ( 2 × 4 orbits = total 8 electrons ).
When the number of Argon valence electron is 8, it makes symmetrical hexahedral structure.
(Fig.10) Each Ar orbit contains two electrons and one hole.
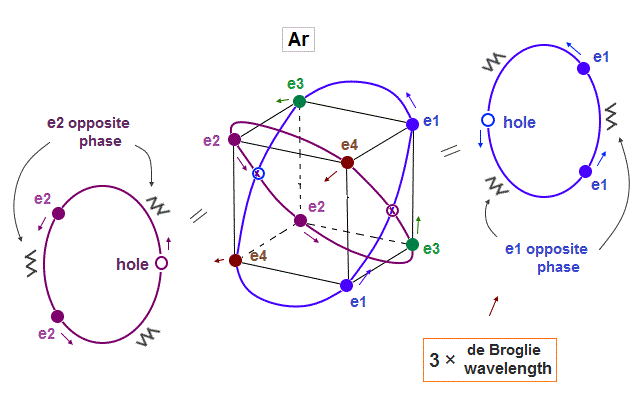
If Argon orbit is 3 × de Broglie wavelength, and each orbit contains two electrons, it must include one "hole". "Hole" is the same phase as the position of each electron, but it doesn't have an electron.
Also in this case of Argon, each two orbits ( ex. "e1" and "e2" ) can cross "perpendicularly", keeping symmetrical distribution.
(Fig.11) Four 3 × de Broglie wavelength orbits in Argon
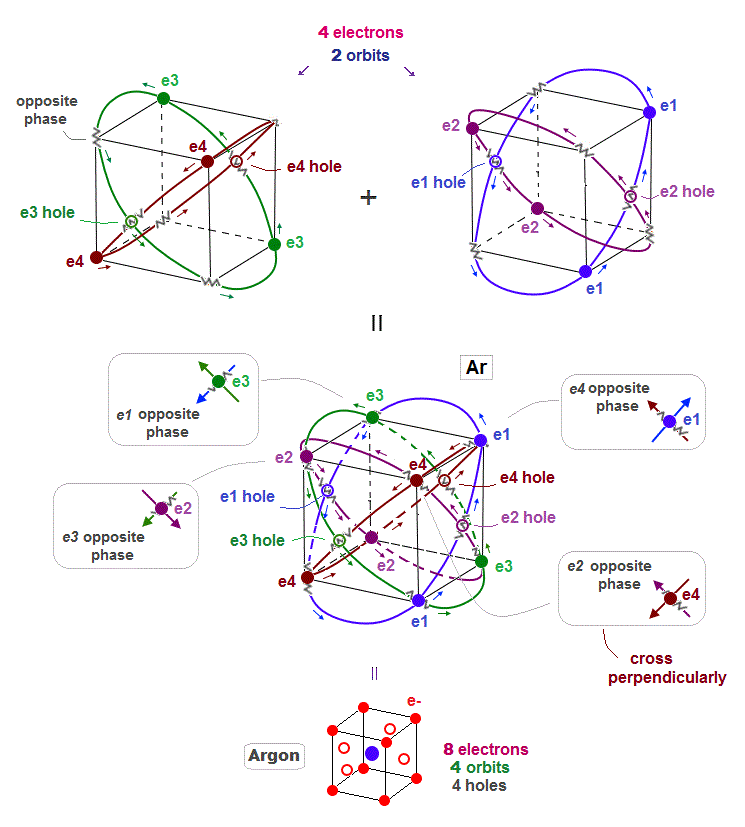
When each Argon orbit is 3 × de Broglie wavelength, how many orbits can Argon have ? Argon can have maximum 4 orbits.
When there are 4 orbits of 3 × de Broglie wavelength, all opposite wave phases just cross each other perpendicularly and become stable like helium.
Different from Neon with 2 × de Broglie wavelength orbit, Argon includes 4 holes.
(Fig.12) Periodic motion of Argon 8 valence elecrons
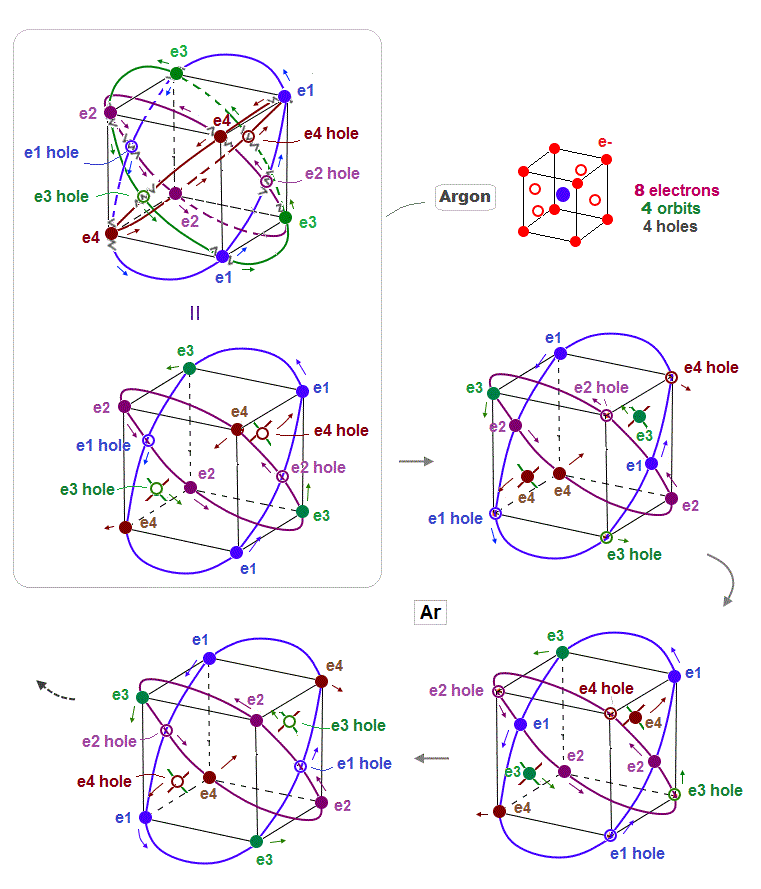
This is periodic motion of Argon 8 valence electrons. Each electron ( or hole ) always crosses its opposite wave phase perpendicularly.
(Fig.13) Total number of Ar valence electrons becomes 12 ( not 8 )
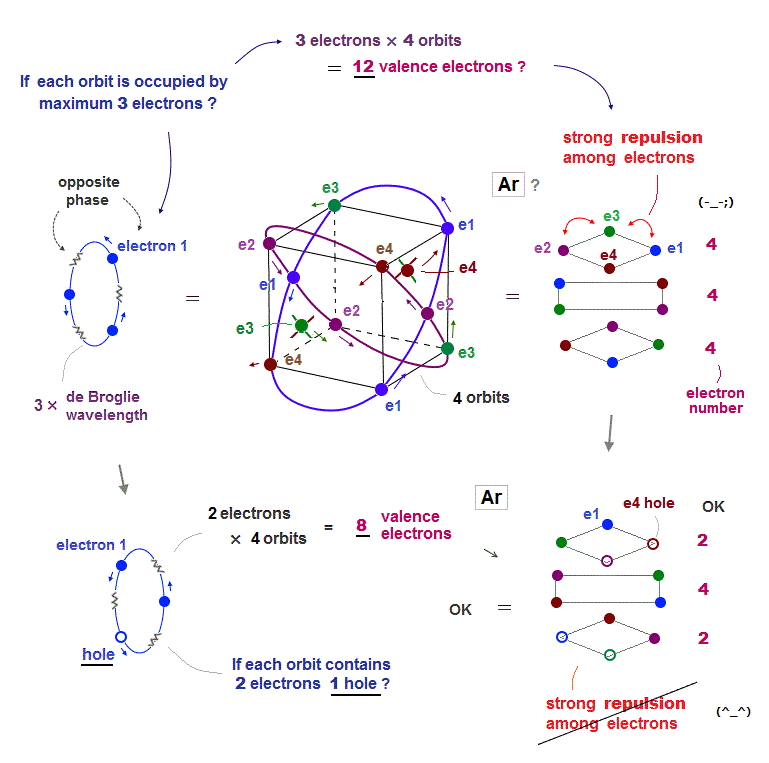
Argon has 3 × de Broglie wavelength orbits, so each Ar orbit can contain up to 3 electrons. So total maximum electron number is 3 × 4 orbits is 12 ?
If Ar each orbit is fully loaded with 3 electrons, Coulomb repulsions among electrons are asymmetrically too strong ( all three layers include 4 electrons in Fig.13 upper ).
To weaken Coulomb repulsion, electrons ( each 2 ) have to be removed from upper and lower layers (= Fig.13 lower ). So when total electron umber of Ar is 8, it is stable.
(Fig.14) Two holes in oxygen form H2O molecular bond
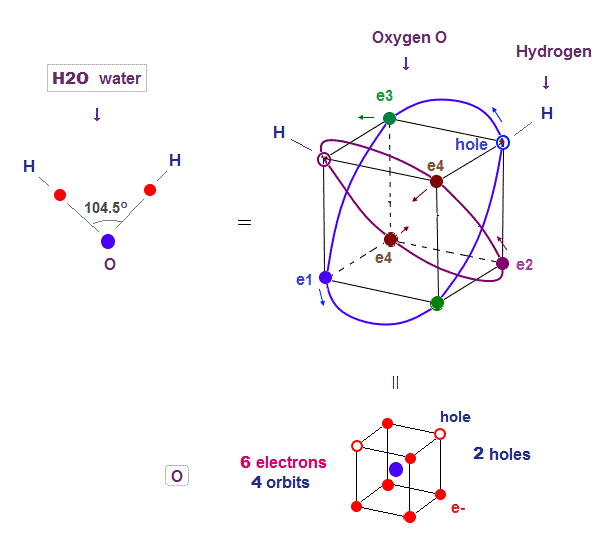
Oxygen (= O ) with 2 × de Broglie wavlength orbits has 4 orbits ( 2 electrons × 2 orbits + 1 electrons × 2 orbits = 6 valence electrons ). So oxygen has 2 holes.
Four 2 × de Broglie wavelength means even this oxygen structure must be close to tetrahedron like carbon.
Due to the asymetrical number "six", tetrahedral structure is a little distorted by Coulomb repulsion also in oxygen.
So its H2O bond angle 104.5o is slightly smaller than pure tetrahedral 109o
(Fig.15) Sulfur (= S ) has 6 electrons and 6 holes. → H2SO4 is formed
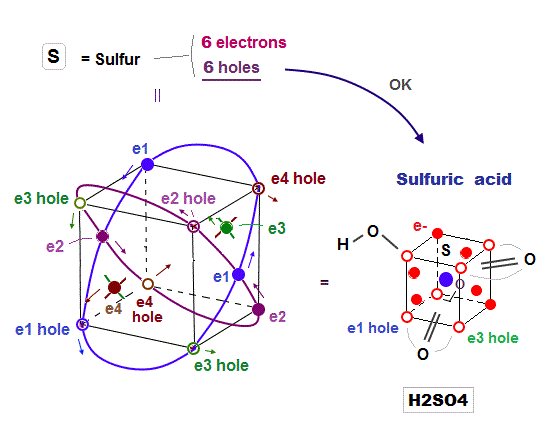
Sulfur (= S ) has 6 valence electrons, which means sulfur can bind to up to 2 electrons to form Argon-like structure ?
But as shown in sulfuric acid (= H2SO4 ), sulfur can bind to up to 4 oxygens to form tetrahedral structure.
Because the sulfur with 3 × de Broglie wavelength orbit has 6 holes enough to accept other atomic electrons and form molecular bond with 4 oxygens.
(Fig.16) Because Oxygen has only "2 holes", and sulfur has "6 holes"
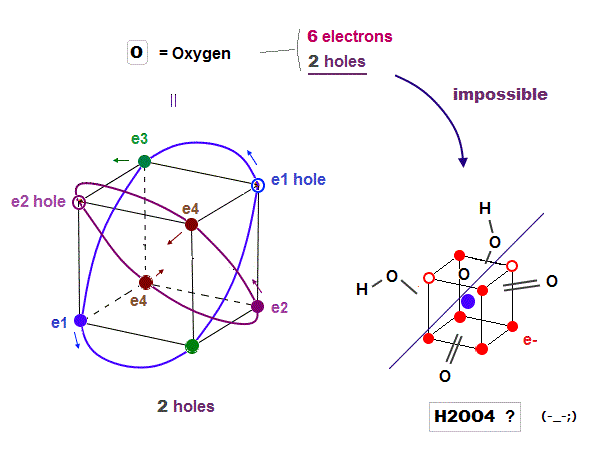
Oxygen (= 6 ) also has 6 valence electrons like sulfur. But oxygen cannot bind to 4 oxygens to form molecules like tetrahedral H2SO4. Why ?
Because oxygen with 2 × de Broglie wavelength orbits has only 2 holes, so there is NO room to accept valence electrons of 4 oxygens in order to form molecular bonds like sulfur.
Ozone hydrogen peroxide (= H2O5 ) has nothing to do with H2SO4
(Fig.17) 6 orbits of Kr outer electrons.
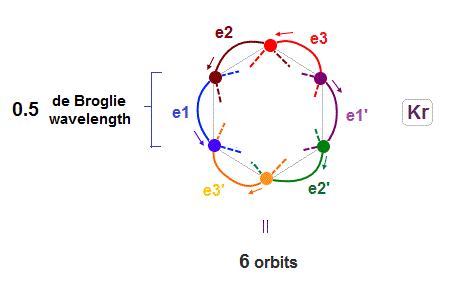
In atoms larger than Neon (= 4 orbits ), Krypton with 4 × de Broglie wavelength has 6 orbits.
Fig.17 is Krypton orbits seen from the upper side.
0.5 × de Broglie wavelength orbit is included between two closest intersections, like Neon and Argon.
(Fig.18) Each orbit of Krypton's outer electrons.
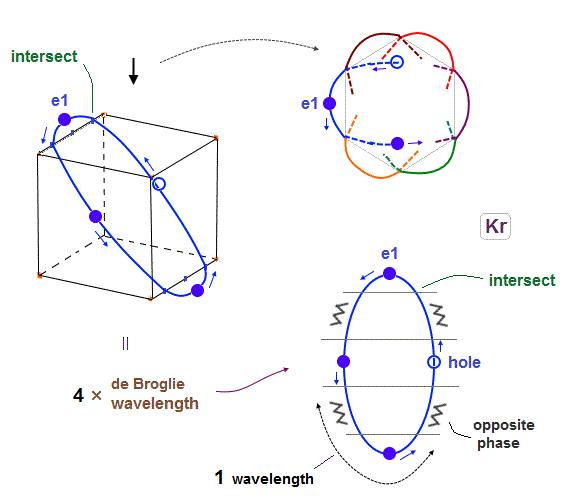
Krypton with six 4 × de Broglie wavelength orbits has 18 valence electrons
Considering the number of Kryoton valence electrons is "18", each 4 × de Broglie wavelength orbit contains three electrons and one hole (= 3 × 6 = 18 ).
When each orbit comes closer to another orbit, these two orbits tend to be perpendicular to each other.
(Fig.19) All opposite wave phases just cross each other
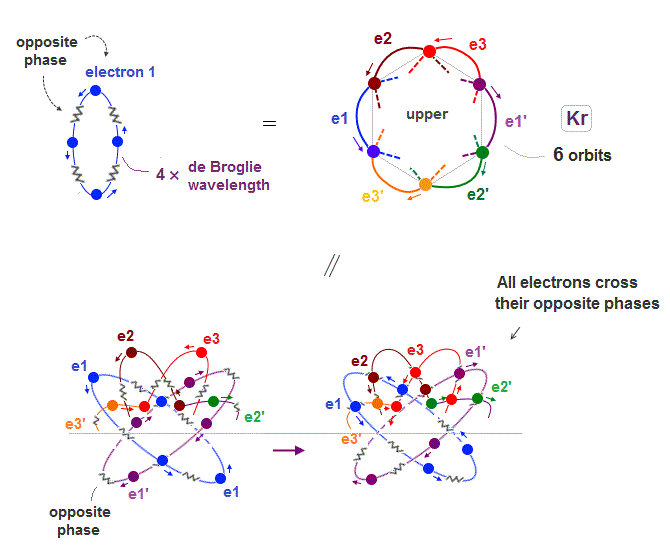
Krypton is in the fourth row of periodic table, which means it has 4 × de Broglie wavelength orbit.
If there are 6 orbits with 4 × de Broglie wavelength, all their electron's opposite wave phases always cross each other, and cancel their magnetic property
(Fig.20) When Krypton contains 24 electrons, their repulsion is too strong
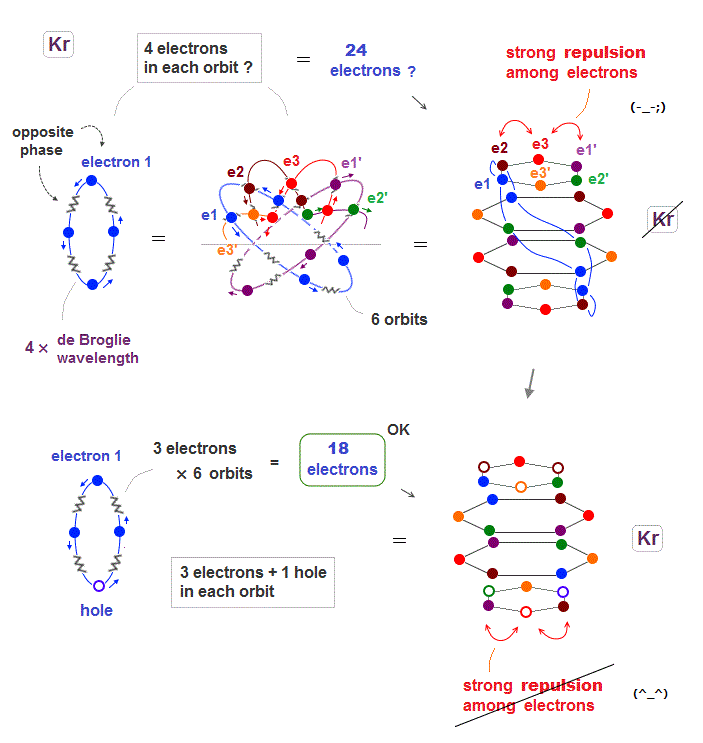
Seeing the fourth row in periodic table including 18 elements, we can think noble gas Krypton has the maximum 18 valence electrons.
When Krypton with 4 × de Broglie wavelength orbits has 6 orbits, it can have the maximum 24 electrons (= 4 × 6 ) ? Unfortunately not.
Kryton orbitals consists of four layers in vertical direction, with each having six electrons, as seen in Fig.20 upper.
But in this case, each six electrons included in the top and bottom layers show stronger Coulomb repulsion than other two middle layers.
So to be symmetric in Coulomb repulsion, the top and bottom orbital layers must decrease electrons in their most stable state ( Fig.20 below ).
Like swing of a pendulum, electrons moving back and forth between unstable and stable states with maximum 18 electrons.
(Fig.21) Each Rn orbit contains 4 electrons and 2 holes.
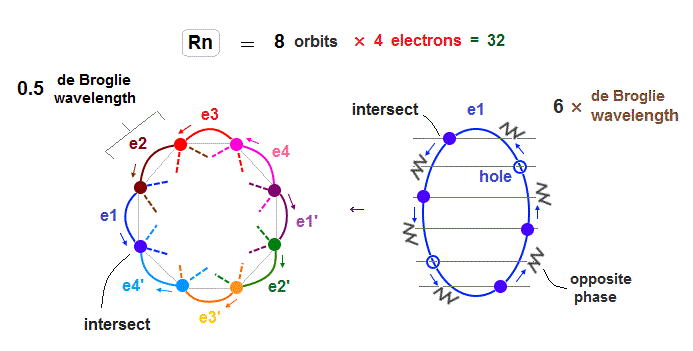
Radon (= Rn ) with eight 6 × de Broglie wavelength orbits has 32 valence electrons.
So in Radon case, we can think each orbit contains only 4 electrons ( + 2 holes ) to avoid stronger Coulomb repulsions and imbalance in its distribution.
(Fig.22) Radon outer electron's motion (= 6 × de Broglie wavelength ).
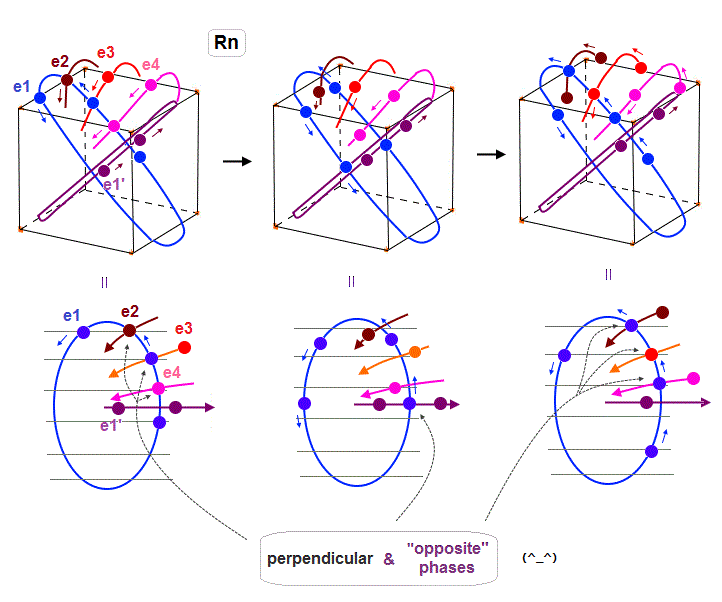
Radon is 6 × de Broglie wavelength, so each orbit includes enough wave "crest" and "trough" to make all 8 orbits "harmonize" and cross each other in just the opposite phases.
In Fig.22 left, e1 ( e2, e4 ) crosses e3 ( e1, e1 ) orbit perpendicularly in the "opposite" phases.
In Fig.22 middle, e1 crosses e1' orbit perpendicularly in the "opposite" phases.
In Fig.22 right, e1 ( e3 ) crosses e2 ( e1 ) orbit perpendicularly in the "opposite" phases.
As a result, we can prove de Broglie wavelength determines the maximum orbital number (= Pauli exclusion principle ), NOT depending on unrealistic spin, which magnetic moment is too weak to influence them.
(Fig.23) If Rn contains 6 electrons × 8 orbits = 48 electrons ..
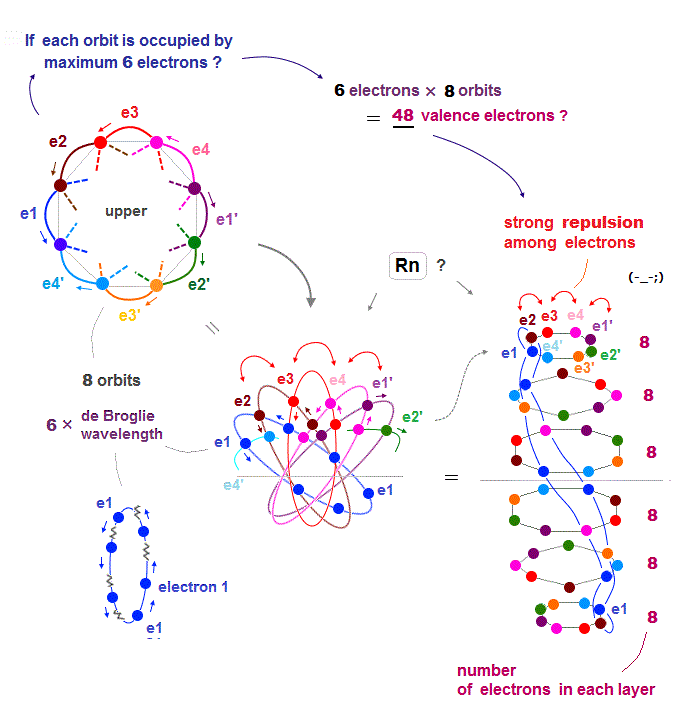
Each orbit of Radon (= Rn ) is 6 × de Broglie wavelength, so each Rn orbit can contain up to 6 electrons. Radon has 8 orbits, then total is 6 × 8 orbits = 48 electrons ?
But the number of Radon valence electron is only 32. Why ? Radon consists of 6 layers like Fig.23 right ( Sorry, this picture of Rn is a little thinner than actual one ).
If each orbit contains maximum 6 electrons, especially in upper and lower layers, Coulomb repulsions among electrons become too strong.
So 48 valence electrons is impossible in Radon.
(Fig.24) Each orbit of Radon contains 4 electrons + 2 holes
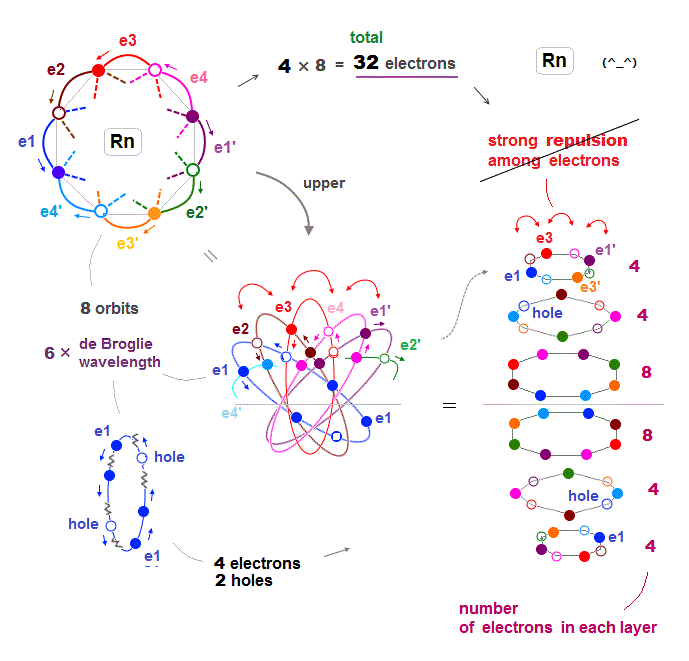
When each orbit of Radon contains up to 4 electrons and 2 holes, Coulomb repulsion among electrons can be weakened, then stable.
As shown in Fig.24 right, interelectronic repulsion especially upper and lower 2 layers is asymmetrically too strong, compared to middle layers.
If we decrease 6 fully loaded electrons to 4 in upper and lower 2 layers, the whole Rn electron distribution becomes symmetric and normal in their Coulomb repulsion.
This is the reason why Radon has 32 (= 4 × 8 orbits ) valence electrons instead of 48 electrons.

2016/9/23 updated. Feel free to link to this site.