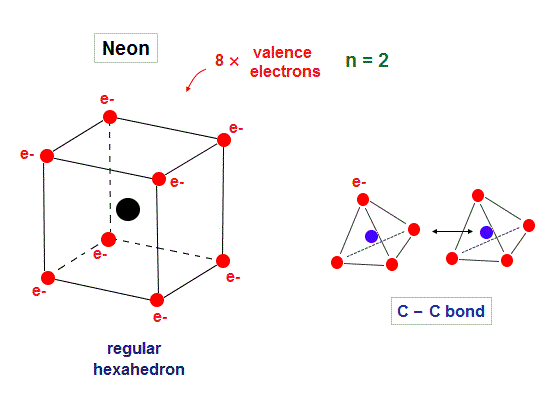
Top page ( correct Bohr model )
New Bohr model carbon, hydrogen bonds.
de Broglie wavelength determines all structures.
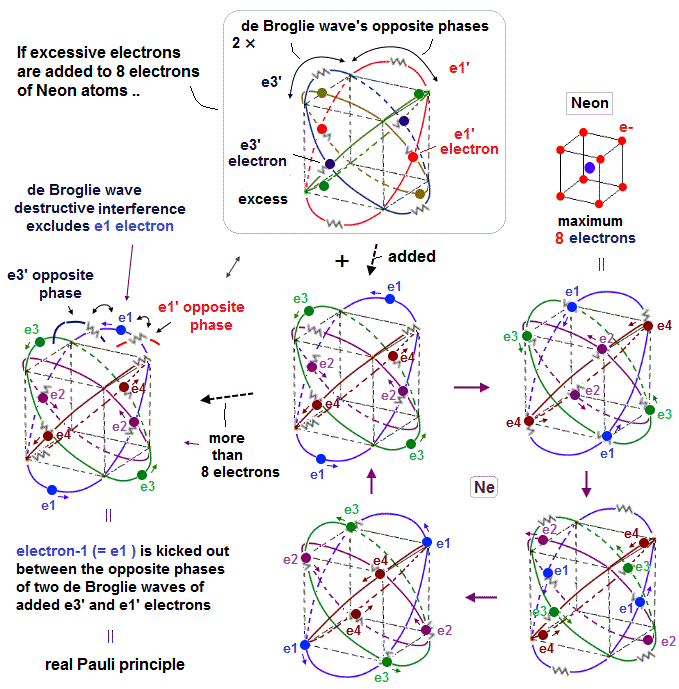
(Fig.1) Eight valence electrons = regular hexahedron.

Neon is stable noble gas, and has eight valence electrons in n = 2 orbitals.
Considering symmetric distribution due to repulsive Coulomb forces, regular hexahedron is natural.
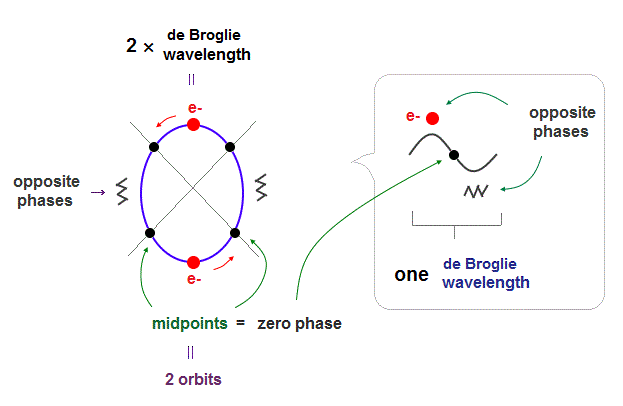
In Bohr-Sommerfeld model, principal quantum number, n = 2 means 2 × de Broglie wavelength orbits.
(Fig.2) 2 × de Broglie wavelength orbits. Each is a pair of opposite phases.
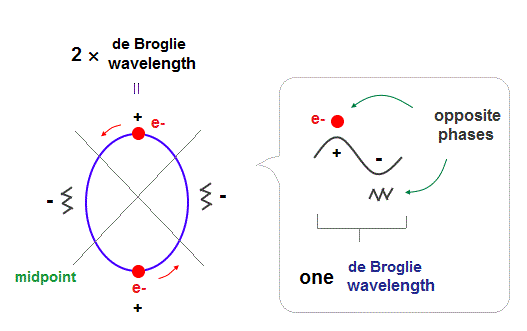
As shown in Davisson-Germer experiment, each de Broglie wavelength consists of a pair of ± phases, which are opposite and cancel each other.
2 × de Broglie wavelength orbits can contain 2 electrons, as shown in Fig.2.
There are 4 midpoints (= 2 midlines ) with zero phases between ±phases.
(Fig.3) Electron 1 (= e1 ) orbit with 2 electrons.
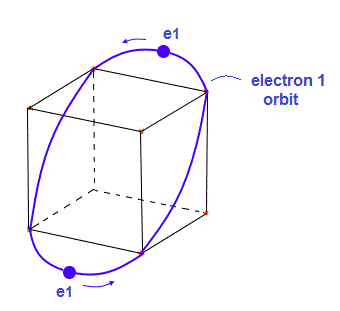
Fig.3 is "e1" orbit containing two electrons on the opposite sides.
This orbit is supposed to be a little elliptical intersecting hexahedron at 4 vertices.
(Fig.4) Electron 2 (= e2 ) orbit "perpendicular" to e1 orbit.
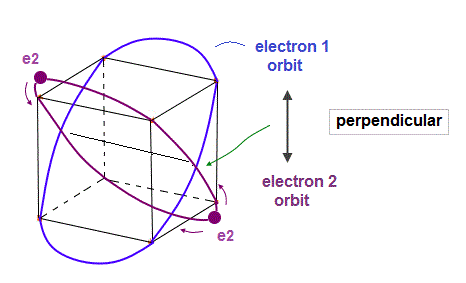
As shown in Fig.4, e2 orbit with 2 electrons crosses e1 orbit perpendicularly at 2 points.
"Perpendicular crossing" is important for avoiding destructive interference.
(Fig.5) Electron (= e3 ) orbit with 2 electrons.
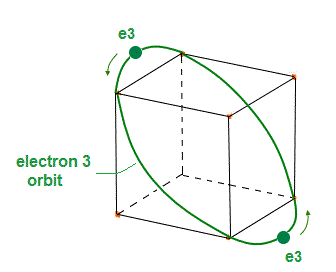
(Fig.6) Electron 4 (= e4 ) orbit "perpendicular" to e3 orbit.
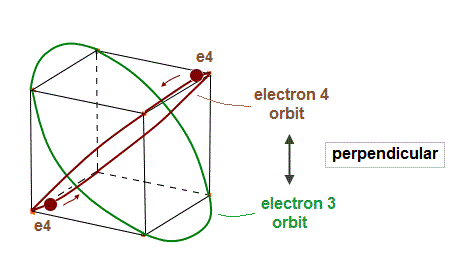
In the same way, e4 orbit crosses e3 orbit perpendicularly at 2 points.
Each orbit contains two electrons.
(Fig.7) "e1" and "e3" orbits cross perpendicularly, too.
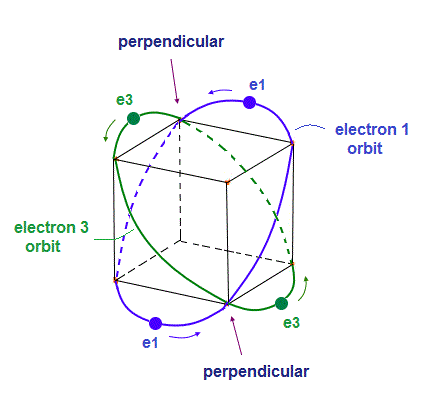
As shown in Fig.7, "e1" and "e3" ( and "e2" and "e4" ) orbits cross perpendicularly at 2 points.
This is the same mechanism as Bohr model helium.
(Fig.8) Starting positions in 4 orbits.
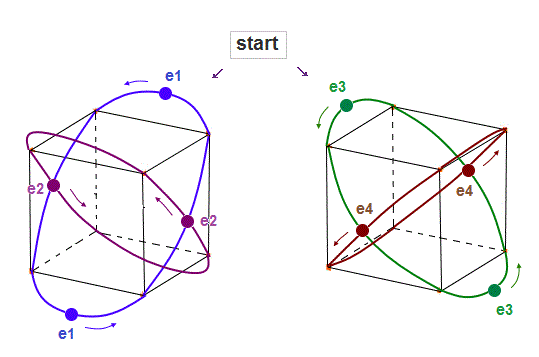
We choose Fig.8 as starting electrons' positions in 4 orbits.
"e2" (or "e4" ) electrons cross "e1" ( or "e3" ) orbit perpendicularly, avoiding destructive interference.
(Fig.9) Each electron can avoid other electrons' de Broglie "annoying" phases.
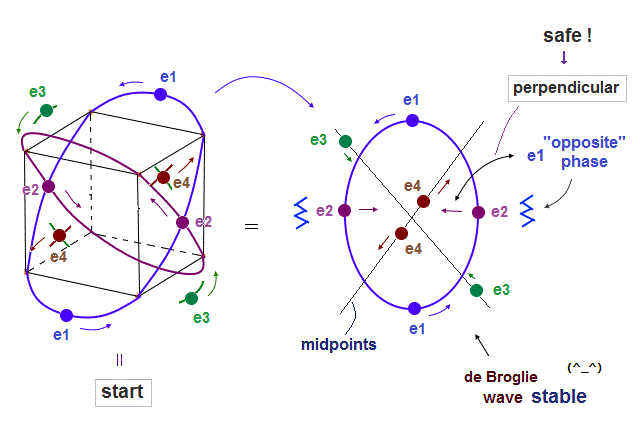
Fig.9 is from the viewpoint of "e1" orbit which e2 orbit crosses perpendicularly.
As shown in Fig.10, 2 × de Broglie wavelength orbit contains 2 midpoint lines with zero phase.
Each of this 2 × "midpoint" lines contain "e3" ( or "e4" ) orbit.
So, total number of Ne orbits is "4" (= "e1", "e2 = perpendicular", "e3, e4 = midpoint lines").
(Fig.10) Midpoints = "Zero" phases have NO influence on other de Broglie waves.
Due to "zero" phases of midpoint, "e3" and "e4" orbits can avoid the bad influences of "e1" wave phases. So each electron can move independently from other de Broglie waves, which means stable.
(Fig.11) Each electron can move independently from other "annoying" phases.
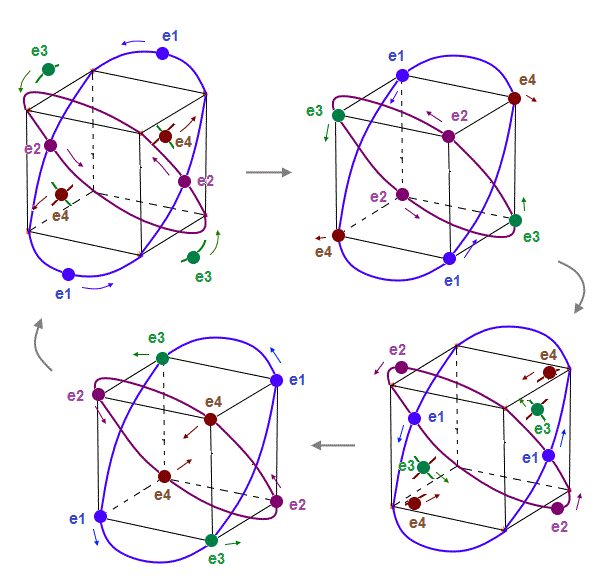
Fig.11 shows the periodic movements of all eight electrons in Bohr model Neon.
Electrons can move smoothly, NOT crashing into other electrons.
(Fig.12) Electrons always cross other "opposite" wave phases, "neutralizing" total phases.
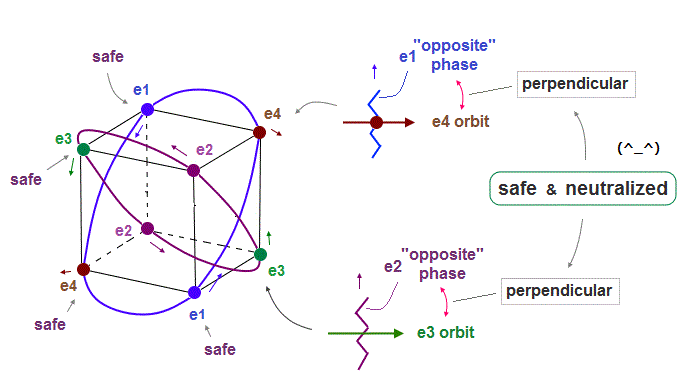
As seen in Fig.11 and Fig.12, each electron can cross other electrons' orbits perpendicularly, when they are opposite wave phases to each other.
"Perpendicular crossing" means each de Broglie wave can avoid destructive interference.
And crossing of "opposite" wave phases can neutralize total wave phases at all points ( ±phases = zero ).
"Neutralization" of wave phases means any other electrons can be free from other wave ( bad ) influences, and move stably and independently, NOT to be disturbed. See also this page.
(Fig.13) Next regular icosahedron cannot make orbits perpendicular to each other.
Next regular polyhedron is regular icosahedron with 12 vertices.
But as shown in Fig.13, each electron in this icosahedron cannot cross other orbits perpendicularly.
Furthermore, 6→6' orbit is independent from other orbtis, meaning "asymmetric".
So, this regular icosahedron structure is unstable for electron's movement.
(Fig.14) The change of the first ionization energy shows us de Broglie wavelength.
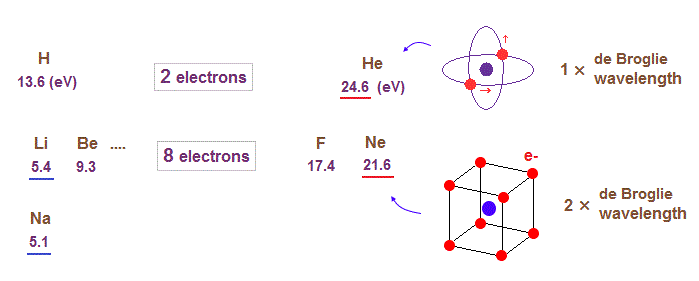
When we look at the change of the first ionization energies of atoms, we can find where the orbital de Broglie wavelengths change.
For example, in the periodic table ( see this, this ), the first ionization energies suddenly decreases in He → Li (= 24.6 eV → 5.4 eV ), and Ne → Na ( 21.6 eV → 5.1 eV ) transitions.
Sudden drop in the ionization energies means de Broglie wavelengths (= orbital radius ) increases by one at these points.
(Fig.15) 2 × 4 orbits make stable regular hexahedron in Ar.
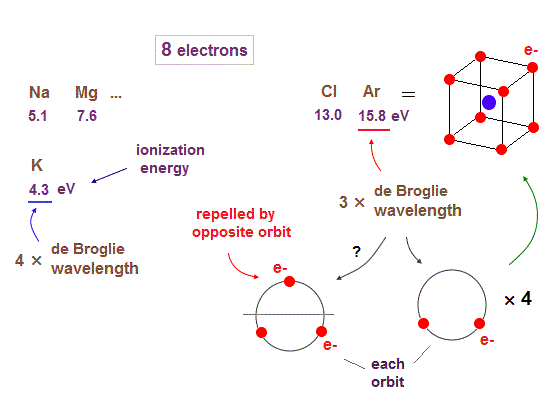
When we see the sudden drop in the first ionization energies from Ar to K ( 15.8 eV → 4.3 eV ), we can understand the orbits of 3 × de Broglie wavelengths end at Ar.
So from K (= potassium ), 4 × de Broglie wavelength orbits start.
Though 3 × de Broglie wavelengths contain total 3 electrons in each orbit, 2 × 4 orbits (= total 8 electrons ) can form stable regular hexahedron like Neon. See Argon structure.
If each orbit contains maximum 3 electrons, one of them always stick out into the opposite sides, which is strongly repelled by other electrons included in the opposite ( other ) orbits.
"2 electrons on one side × 4 orbits" can form stable regular tetrahedron-like distribution from the veiwpoint of each orbit. ( tetrahedron is a part of hexahedron. )
(Fig.16) Ionization energies show us "where" de Broglie wavelengths change.
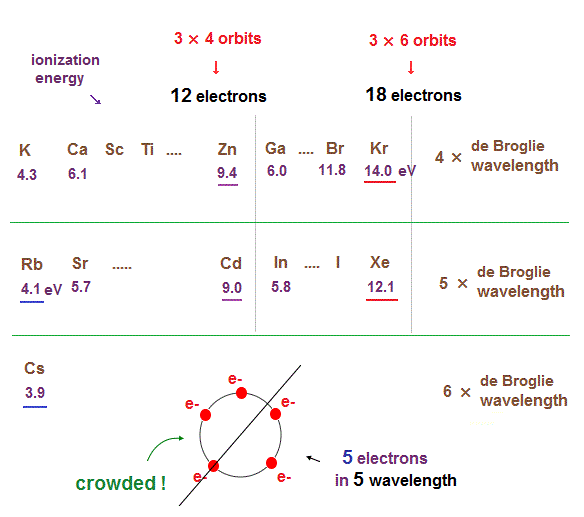
In the same way, sudden drop in inonization energies show us "Kr" and "Xe" are the last atoms in 4 × and 5 × de Broglie wavelength orbits.
As seen in this and this, the changes of ionization energies from "4s" to "3d" orbitals are too smooth, meaning "4s" and "3d" are the same type of orbits. Quantum mechanical orbitals are too artificial.
As de Broglie wavelengths (= orbtial radius ) get bigger, the spaces between each orbits get wider.
So "packing" maximum electrons into one single orbit ( 5 electrons in 5 wavelength orbit ) causes strong repulsive Coulomb forces due to the imbalance of electron's distributions in all space.
In Kr and Xe, we consider each orbit contains 3 electrons and makes 6 vertices of regular octahedron ( 3 × 6 = 18 ).
If each orbit contains maxium electrons ( ex, 4 electrons in 4 de Broglie wavelengths ), half of them tend to crash into other orbital electrons on the opposite side. See this page
(Fig.17)
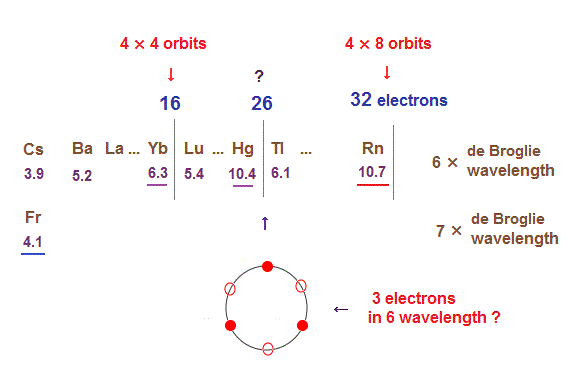
As I said in this section, as de Broglie wavelengths increases, the midpoint lines (= zero phase ) increases in number, meaning they can contain more orbits stably.
In 6 × de Broglie wavelength orbit of Rn, the total 8 orbits can be included due to increased midpoints. So 4 electrons ( in each orbit ) × 8 orbits become 32 electrons in Rn atom.
Different from 4 or 5 × de Broglie wavelength, the electron's distribution in orbits of 6 × wavelength tend to spread symmetrically, when its included number is "3" and "4".
So when the number of electrons is small, this symmetrical distributions in each orbit obstruct other orbit from being on the opposite side.
It is thought that atomic stability is a little more complicated in "Hg" (= 26 outer electrons ).
(Fig.18) Maximum orbits = midpoint lines + 2 (= two perpendicular orbits )
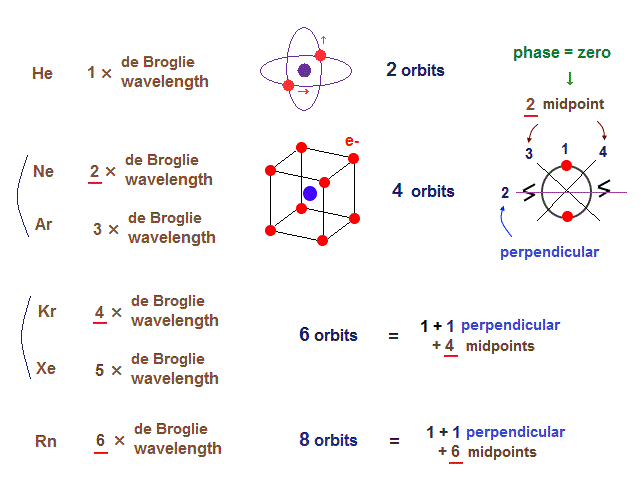
When each orbit crosses another orbit perpendicularly, they can avoid destructive interference.
When atoms contain more than two orbits, other orbits must be on the midpoint lines (= zero phase ) NOT to be disturbed.
So, the maxium number of orbits in Ne becomes "4" (= 2 × perpendicular + 2 × midlines ).
4 × de Broglie wavelength contains 4 midlines, so the total orbital number of Kr becomes "6".
The odd numbers of "3", "5", "7" orbits are asymmetrical and unstable.
So the orbital numbers of "Ar" (= 3 × waveslength ), "Xe" (= 5 × waveslength ) remain the same as "Ne" and "Kr".
So we can get the generalized common rules, "perpendicular orbits" and "avoiding destructive interference" in all atoms based on de Broglie wavelength.

2015/3/25 updated. Feel free to link to this site.