(Fig.1) If we try to make the three-electron wavefunction mixing the up and down spins, this wavefunction vanishes by canceling the plus and minus terms due to the paradoxical quantum mechanical Pauli antisymmetric rule !
Textbooks often write about two-electron helium and hydrogen molecule, but rarely mention three-electron atoms such as Lithium or molecules.
Because quantum mechanical Pauli principle is unable to treat all atoms and molecules with more than two electrons mixing the up and down or spacial symmetric and antisymmetric wavefunctions ( this p.3-6, or this-(1)-(11) ) !
In the upper figure, the atom-A has an electron with down-spin (= down-spin ↓ is often denoted as β ), the atom-B has an electron with up-spin (= up-spin ↑ is often denoted as α ), and the atom-C has an electron with up-spin.
So the molecular bond attractive exchange energy based on spatial symmetric wavefunctions (= singlet ) between two up-down anti-parallel spins must be generated between an electrons-1 in A wavefunction (= down-spin ) and an electron-2 in B wavefunction (= up-spin ), and between electrons-1 in A wavefunction (= down-spin ) and electron-3 in C wavefunction (= up-spin ).
See this p.2, this p.1-4, this p.8, this p.22
And the Pauli repulsive exchange energy based on spacial antisymmetric wavefunction (= triplet ) between the same up-up spins must be generated between electrons-2 in B wavefunction (= up-spin ) and electron-3 in C wavefunction (= up-spin ).
↑ These spatial symmetric and antisymmetric wavefunctions have different inconsistent normalization coefficients, so all these separate wavefunctions must be united into one wavefunction mixing spacial symmetric and antisymmetric wavefunction to explain atoms and molecules with more than two electrons, though this is impossible in the quantum mechanical Pauli antisymmetric wavefunctions.
For example, we prepare one term which is the product of three atomic wavefunctions of φA↓(1) (= atomic-A wavefunction with down spin containing the electron-1 ), φB↑(2) (= atomic-B wavefunction with up spin containing the electron-2 ), and φC↑(3) (= atomic-C wavefunction with up spin containing the electron-3 ) = φA↓(1)φB↑(2)φC↑(3).
When exchanging two electrons 1 and 2, this term's sign should remain unchanged as "positive", and this term's electrons' labels change into φA↓(2)φB↑(1)φC↑(3), because the electron-1 exists in the atomic-A wavefunction with down spin and the electron-2 exists in the atomic-B wavefunction with up spin, which must form the spatial symmetric wavefunction (= singlet ) with respect to interchanging two electrons 1 and 2 in these terms.
Next we exchange the electron 2 and 3 in this second term of φA↓(2)φB↑(1)φC↑(3), which changes into φA↓(3)φB↑(1)φC↑(2)
↑ No sign change of these spatial symmetric wavefunctions, because the electrons-2 and 3 exist in the atomic-A with down spin and the atomic-C with up-spin. = the up-down spin wavefunction must be symmetric (= singlet ) which doesn't change the sign under the exchange of two electrons.
In the same way, when we exchange two electrons 2 and 3 in the first term of φA↓(1)φB↑(2)φC↑(3), this term flips its sign like -φA↓(1)φB↑(3)φC↑(2).
↑ Because the electrons-2 and 3 exist in the atomic-B wavefunction with up-spin and the atomic-C wavefunction with the same parallel up-spin, hence, these two electrons with the same up-up spin must form the spacial antisymmetric wavefunction (= triplet ) which must change its sign under the exchange of two electrons' coordinates or labels.
And if we exchange two electrons 1 and 3 in this term of -φA↓(1)φB↑(3)φC↑(2), this does not change the sign like -φA↓(3)φB↑(1)φC↑(2).
↑ because the electrons 1 and 3 exist in the atomic-A with down spin and the atomic-B with up spin, which must form the spatial symmetric wavefunction (= singlet ) in the term of -φA↓(1)φB↑(3)φC↑(2).
As a result, this three-electron molecule needs the contradictory terms of plus (= φA↓(3)φB↑(1)φC↑(2) ) and minus ( -φA↓(3)φB↑(1)φC↑(2) ) signs, which cancel each other !
↑ This result shows the quantum mechanical Pauli principle cannot be applied to the case of three electrons or more than two electrons mixing up and down spins.
Only the spatial wavefunction (= not spin part ) is important, contributing to the total energy, but the contradictory quantum mechanical singlet-triplet rule cannot obtain the legitimate spacial wavefunction for three-electron Lithium separated from spin part ( this p.12-third-paragarph ).
For example, the three-electron Lithium (Hylleraas) wavefunction ( this p.3-(6) ) must contain the paradoxical terms like the exchanging the 1st and 3rd electrons (= exchanging the 1st and 3rd wavefunctions ) paradoxically changes the sign φ(1,2,3) → -φ(3,2,1) or does Not change the sign -φ(2,3,1) → -φ(1,3,2), which is inconsistent with respect to symmetric or antisymmetric wavefunctions under exchanging two electrons, and disagrees with the original Pauli antisymmetric rule.
(Fig.2) In Pauli antisymmetric wavefunction or Slater determinant, only Pauli repulsive exchange energy with the same spins or triplet remains. Any singlet exchange energies (= molecular attractive bond ) with the up-down spins are zero.
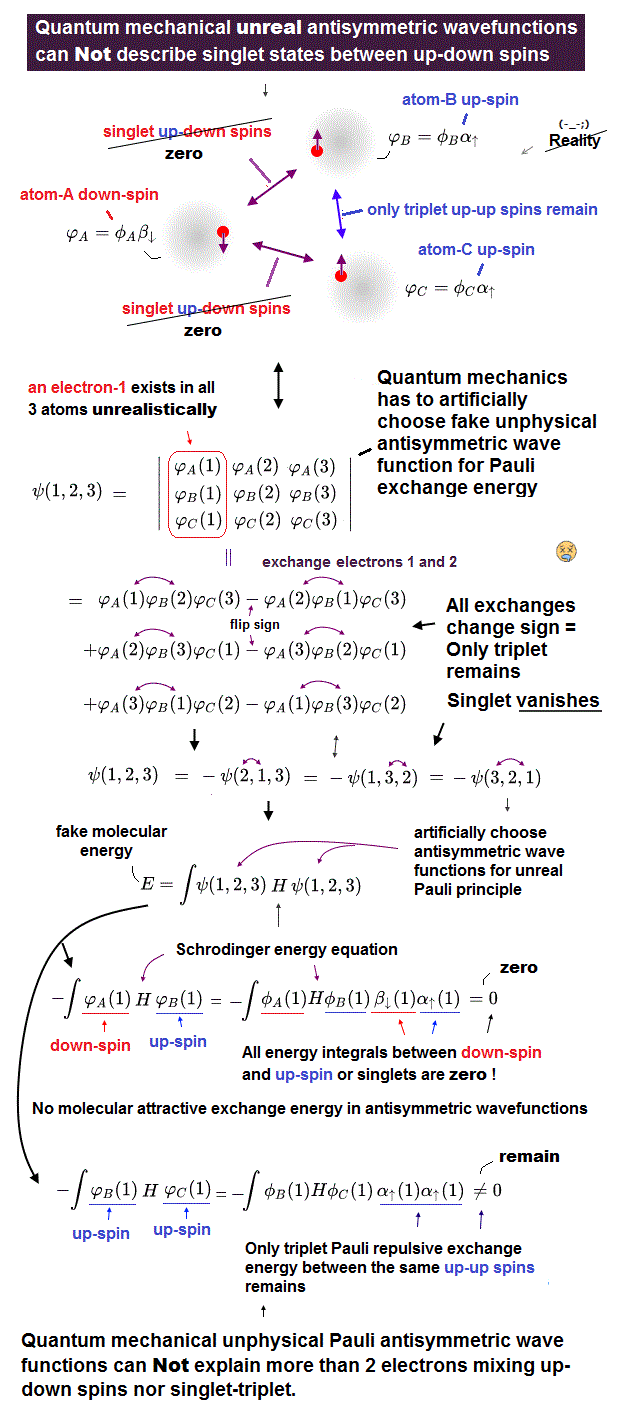
Quantum mechanical Pauli principle cannot describe atoms or molecules with more than two electrons mixing singlet and triplet spins, which means quantum mechanics cannot describe the multi-electron wavefunction mixing spacial symmetric wavefunction (= causing molecular bond attractive exchange energy between up-down singlet spins, this p.3 ) and antisymmetric wavefunction (= causing Pauli repulsive antibond exchange energy between up-uo or down-down triplet spins ).
To deal with this serious paradox, quantum mechanics artificially changed the rule, and started to say all multi-electron atomic and molecular wavefunctions must be expressed only as (nonphysical Pauli) antisymmetric wavefunctions (= No symmetric spacial wavefunctions ) or Slater determinant ( this p.1-5 ) where No molecular bonds expressed as attractive symmetric exchange energies (or No bonding exchange integral ) can be generated when atoms or molecules contain more than two electrons. ← No molecular bonds ! It means quantum mechanics is false.
In quantum mechanics, all wavefunctions must be expressed as Pauli antisymmetric wavefunctions or Slater determinants ( this p.7-8 ) where each atomic wavefunction consists of spatial wavefunction and spin wavefunction parts (= α↑ is up-spin, and β↓ is down-spin ).
In exchange integrals of two different atomic wavefunctions, the spin integral of two different up (= α↑ ) and down (= β↓ ) spins always becomes zero (= ∫αβ = 0 = No molecular bond attractive exchange energy between the different up-down spins ), and only the spin-integral of two same up-up or down-down spins remains as non-zero (= only Pauli repulsive antibonds between the same up-up or down-down spins remain ) in atoms or molecules with more than two electrons ( this p.4-spin-selection-rule ).
↑ It means in quantum mechanics, No molecular attractive exchange energy integral between two different up-down spins is generated (= No molecular bonds in quantum mechanics ! ), and only unnecessary Pauli repulsive exchange energy between the same up-up or down-down spins remains ( this p.5-6, this p.37, this p.10-lower ).
This is a fatal flaw of quantum mechanical Pauli principle based on unphysical antisymmetric wavefunctions.
(Fig.3) ↓ Singlet-triplet theory is contradictory in Pauli principle of more than two electrons, so quantum mechanics is false.
In two-electron helium atom, quantum mechanics insists there is difference between the energy levels (= ex. 1s2p of helium ) of singlet (= 1P ) expressed as spin-up ↑ (= α ) and spin-down ↓ (= β ) and triplet (= 3P = spin-up-up, spin-up-down, spin-down-down symmetric ) wavefunctions ( this p.9 ).
But as shown in this, this quantum mechanical singlet-triplet theory is invalid in more than two electrons such as lithium.
So quantum mechanics illegitimately changed the original Pauli principle definition based on the helium-singlet-triplet states into generalized atomic Pauli principle version expressed as Slater determinant or Pauli antisymmetric wavefunction where each wavefunction consists of spatial (= φ ) and spin (= α-up-spin, β-down-spin ) parts (= which contains No spatial symmetric wavefunction even in spin-up-down ↑↓ case ).
The problem is this generalized Pauli principle antisymmetric wavefunction or Slater determinant can Not distinguish singlet and triplet energy levels. = There is only one form of antisymmetric wavefunction (= two terms connected by minus ) with two electrons of spin-up and down, as shown in the above figure.
Some people say combining two Slater determinants by exchanging spins between two wavefunctions can distinguish these singlet and triplet states ( this p.4-9 ).
↑ But this method based on swapping spins between two atomic wavefunctions cannot be used in cases of more than two electrons.
So in all atoms with more than two electrons, the original singlet-triplet theory ( this p.8 ) is invalid, which is inconsistent with the quantum mechanical claim that even magnesium and calcium with more than two electrons should have singlet and triplet energy levels.
This clear self-contradiction shows quantum mechanics is wrong.
Beryllium (= Be ) and singly-ionized boron (= B+ ) have exactly the same structure with two valence electrons, so these two atoms should have the same-order energy levels.
But the orders of 2s3s and 2p2 between Be and B+ are completely different and inconsistent.
Boron (= B ) and singly-ionized carbon (= C+ ) also have exactly the same electron structure with the three same valence electrons, but the energy positions of 2s23s are completely different between B and C+, which is contradictory.
Helium's three energy levels of 1s2p triplet (= 3P = 2,1,0 ) are inconsistent with beryllium's (= 2s2p ) and magnesium's (= 3s3p ) triplet states' order 3P = 0,1,2. ← No legitimate consistent explanation in quantum mechanics.
In boron with three valence electrons, the 2s-2p2 state splits into five different energy levels (= 4P + 2D ), while in aluminum that also has three valence electrons, the same type 3s-3p2 state splits into only three energy levels (= 4P ), which is inconsistent (= Aluminum paradoxically ignores 3p2 singlet inside 3s-3p2 state ). ← Singlet-triplet based on the original Pauli principle becomes invalid in three valence electrons.
In carbon with four valence electrons, 2s2-2p2 splits into five states (= probably they assume three triplets + two singlets in 2p2 inside 2s2-2p2, ) while the same type 2s2-2p3p paradoxically splits into ten states (= only this includes two types of triplets ), though 2s2-2p2 and 2s2-2p3p should have the same types of triplet.
In neon with eight valence electrons where they probably try to treat the 6 electrons as one independent singlet state with spin-zero, then, they should split the remaining 2p-3s (of 2p53s ) into three triplet + one singlet like helium and beryllium, but they split 2p53s into two pairs irrelevant to the original triplet-singlet theory, which is inconsistent.
(Fig.4) Molecular orbital (= MO ) theory requires each single electron to exist in multiple different atoms simultaneously, which also causes unrealistically-inseparable electrons or atoms, and MO cannot avoid unnecessary Pauli repulsive exchange energy, so false.
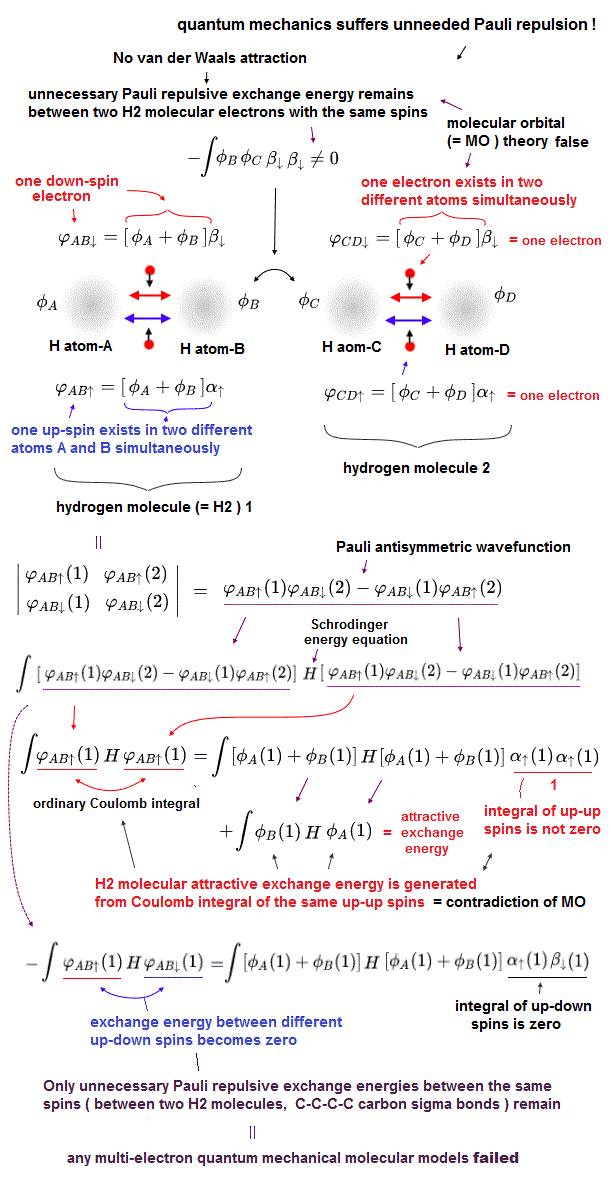
Quantum mechanical Pauli principle expressed as antisymmetric wavefunction or Slater determinants have fatal flaws, and it can Not describe any molecular bond attractive exchange energies between the different up-down spins, and only unnecessary Pauli repulsive exchange energies between the same up-up or down-down spins remain.
To handle this quantum mechanical contradiction, the molecular orbital theory (= MO ) was invented, though this ad-hoc molecular orbital theory cannot eliminate unnecessary Pauli repulsion after all, either.
In this ad-hoc molecular orbital theory, each single electron must always spread over more than one atoms or orbitals = each electron's molecular orbital always becomes a linear combination of multiple atomic wavefunctions ( this p.7(or p.5), this p.4, this p.3 ). ← This unrealistic condition is necessary for generating the fictitious molecular bond attractive energies in MO by avoiding the vanishing attractive exchange energies between the up-down spins.
It means electrons of molecular orbital theory are unrealistically inseparable into different atoms due to their constantly-spreading molecular orbitals, and the ad-hoc molecular orbitals cause non-existent ionization states ( this p.27, this p.14-15-(11)-(13) ), hence, the molecular orbital theory often failed to explain experimental results ( this p.25 ).
This molecular orbital wavefunction also has to be expressed as the unphysical Pauli antisymmetric wavefunction or Slater determinant consisting of multiple molecular orbitals ( this p.14, this-(9.6.1)-(9.6.2) ) where each orbit consists of a spatial molecular orbital (= linear combination of multiple atomic orbitals ) and spin part.
↑ This means the molecular orbital theory also causes unnecessary Pauli repulsive exchange energy between two molecular orbitals with the same spins, which means any quantum mechanical multi-electron models failed to incorporate Pauli principle expressed as the antisymmetric wavefunctions or Slater determinants.
To avoid this unnecessary Pauli repulsive exchange energies, all molecular orbitals must be "orthogonal" to each other, which means all exchange energies or overlap integral between any two different molecular orbitals must be zero ( this p.6, this p.3 ).
↑ When any exchange energies (= or overlap integral ) between two different orbital wavefunctions become zero due to their orthogonal wavefunction's relationship regardless of their spin states, neither molecular bond attractive exchange energies nor annoying unneeded Pauli repulsive exchange energies seem to appear in the energy calculations. ← But even these artificial "orthogonal" wavefunctions cannot avoid unnecessary Pauli repulsive energies after all, so the molecular orbital theory is wrong, as I explain later.
If all exchange energy integrals become zero due to artificially choosing the orthogonal molecular orbital wavefunctions, how does the ad-hoc molecular orbital theory generate the molecular attractive (or Pauli repulsive ) exchange energies, though the exchange energy is zero ?
As shown in the upper figure, even if exchange energies or exchange integrals are zero due to the artificially-chosen orthogonal wavefunctions, the normal Coulomb integral parts (= the product of two same wavefunctions with the same spin ) automatically contain the molecular attractive exchange energies caused by each molecular orbital which is a linear combination of multiple atomic orbitals, which is the trick of molecular orbital theory to generate molecular attractive exchange energies.
Each molecular orbital = ψ = φA(1) + φB(1), hence, the normal Coulomb integral of ∫ |ψ|2 = ∫ | φA(1) |2 + | φB(1) |2 + ∫ 2 φA(1)φB(1) ← the attractive exchange energy +∫φA(1)φB(1) is automatically contained in the normal Coulomb integral of each single molecular orbital.
The problem is that it is basically impossible to make all exchange energies between all different combinations of different molecular orbitals zero or orthogonal, especially in the spherical s atomic orbital like in hydrogen 1s atomic wavefunctions (= exchange integral of two different hydrogen atomic 1s orbitals cannot be zero or orthogonal ).
Molecular orbital theory tries to make artificial orthogonal wavefunctions combining plus (= bonding, this p.68 ) and minus (= antibonding ) phases of atomic wavefunctions ( this p.1-(2) ), but the orthogonal wavefunctions or zero exchange energies mean the overlap region between two orbitals are artificially removed (= which equals the sharpened de Broglie wave increasing Pauli repulsive kinetic energies, this p.49-51 ), hence, the artificially-created orthogonal wavefunctions also include unnecessary Pauli repulsive exchange energies in their Coulomb integral, after all.
So the ad-hoc molecular orbital theory cannot handle intermolecular van der Waals attraction or molecular sigma bonds such as C-C-C-C multiple carbon bonds due to its inability to eliminate unnecessary Pauli repulsion especially between two atomic spherical s orbitals.
Impractical time-consuming configuration integral (= CI ) tries to use unphysical negative exchange energy between two fictitious electrons in different Slater determinants to lower the total energy, which CI trick is ad-hoc and completely unrealistic.
Physicists gave up the theoretical prediction based on this failed molecular orbital theory or multi-electron quantum mechanical model, and instead, invented the empirical Huckel method which can treat only π bonds at first (= because p orbital originally consists of plus and minus phases, and their π bond molecular orbitals can easily become orthogonal ) by artificially adjusting free semi-empirical energy parameters obtained from experiments ( this p.4 ), which cannot predict any molecular enregies or treat spin exchange energies ( this p.2-2nd-last paragraph ).
As shown here, quantum mechanical Pauli principle expressed as unphysical antisymmetric wavefunctions or Slater determinants intrinsically contradict multi-electron atomic or molecular wavefunctions.
This is why only unrealistic one-pseudo-electron approximation called density functional theory (= DFT ) remains as the most-widely used quantum mechanical calculation tool, though this DFT also failed to incorporate Pauli principle.
(Fig.5) Helium (= He ) atom contains two electrons A, B with up and down spins. H atom contains one electron C with up spin. In this case, unnecessary Pauli repulsion occurs between He and H atoms due to zero singlet attractive exchange energy between A and C electrons.
As shown in this, quantum mechanical Pauli antisymmetric wavefunctions or Slater determinants can Not describe cases containing more than two electrons or mixing singlet-triplet spins.
We think about the case where one helium atom (= He ) contains two electrons A (= φA ) and B (= φB ) with up-down spins, and one hydrogen atom (= H ) contains one electron with up spin, as shown in upper figure.
In this case, we can make the singlet or attractive (= positive ) exchange energy between A and B electrons only inside He atom by combining two Slater determinants swapping two up-down spins of A and B electrons of He atom.
↑ But even in this case of using multiple Slater determinants, we can Not express the singlet attractive exchange energy between A electron with down spin of He atom and C electron (= φC ) with up spin of H atom, so unnecessary Pauli repulsive exchange energy remains, which cannot describe van der Waals attraction between H and He atoms.
So quantum mechanical Pauli antisymmetric wavefunctions or Slater determinants are proved to be wrong.
As shown in the upper figure, we prepare two Slater determinants where one Slater determinant (= Slater-1 ) contains A electron with down-spin and B electron with up-spin inside He atom, and the other Slater determinant (= Slater-2 ) contains A electron with up-spin and B electron with down spin inside He atom.
↑ The up-down spins of A and B electrons inside He atom were swapped between two determinants that can generate artificial singlet between A and B electrons ( +∫φA ↓(1) φB ↓(1) = positive attractive exchange energy between two wavefunctions A and B with the same down-down spin which integral does not vanish, ← integral of spin up-down vanishes ).
The total wavefunction of Slater-1 determinant minus Slater-2 determinant can generate the singlet (= positive ) attractive exchange energy between A and B electrons with up-down spins (- correctly, changing the original two-up-down spins inside He into two up-up or down-down spins between two Slater determinants ) inside He atom (= But A and B belong to the same He 1s wavefunction, so actually No exchange energy occurs between the singlet A and B up-down spins, so meaningless ).
↑ In this case, only Pauli repulsive (= negative ) exchange energies occur between A electron of He and C electron (= φC ) of H, and between B electron of He and C electron of H, which causes unnecessary Pauli repulsion between He and H atoms due to each antisymmetric Slater determinant (= which case corresponds to this-middle-Symmetry of three-electron wave functions ).
And as shown in the upper figure, in this case, the strengths of the singlet molecular attractive exchange energy and the triplet Pauli repulsive exchange energy are asymmetric and different, which contradicts the fact.
If we try to artificially generate the molecular attractive ( positive ) exchange energy also between A electron with down spin of He and C electron with up spin of H atom, and swap the down-spin of A electron and the up-spin of C electron, the He atom ends up containing A electron with up spin and B electron with the same up spin, and this He atom with two same up-up spins vanishes by Pauli antisymmetric wavefunction inside one Slater determinant ( this figure-lower ).
So it is impossible to make artificial singlet attractive exchange energy between A electron of He and C electron of H atom even by using multiple Slater determinants.
As a result, we can prove quantum mechanical antisymmetric wavefunctions or Slater determinants are false, unable to describe molecular bond attractive exchange energy between different atoms.
(Fig.6) DFT replacing the whole many-electron material by only one pseudo-electron model with artificially-chosen pseudo-potential is not only unable to explain Pauli principle but also obstructing the real atomic science advancement forever.
After all the ad-hoc multi-electron quantum mechanical molecular models failed to incorporate Pauli principle expressed as antisymmetric wavefunction, almost all physicists started to rely on the unphysical density functional theory (= DFT ) or Kohn-Sham theory which unrealistically treats all different electrons and atoms inside many-electron materials as only one inseparable pseudo-electron approximate model using only one electron's coordinate (= r ) in almost all fields of physics and chemistry in vain ( this p.3-5, this p.6-upper ).
As I said, this unrealistically-inseparable electron of quantum mechanics and its most-widely-used approximate DFT model (= often combined with impractical pseudo-classical molecular dynamics ) are the main culprit of stopping our basic and applied science progress forever.
First of all, this DFT using only one pseudo-electron or one electron's variable (= only one electron's coordinate r ) in any complicated multi-electron molecules cannot describe the original multi-electron Pauli antisymmetric wavefunction which becomes zero when it contains only one electron's variable.
Pauli antisymmetric wavefunction = φA(1)φB(2) - φB(1)φA(2) → φA(1)φB(1) - φB(1)φA(1) = 0, when this contains only one electron-1 like one-pseudo-electron DFT where the original Pauli principle's antisymmetric wavefuntion does Not work. ← The current mainstream quantum mechanical DFT is self-contradictory and wrong.
DFT changes multi-electron potential energies into fictitious pseudo-potential energy based on only one pseudo-electron called exchange-correlation functional potential energy, whose exact universal potential energy form is unkown ( this p.27 ), and physicists must artificially invent and choose this DFT fictitious exchange-correlation potential functional ( this p.6 ).
↑ Artificially-choosing pseudo-potential functional energy and one-pseudo-electron's self-interaction error mean DFT itself is unable to predict any atomic properties (= DFT tries to obtain deceptive relative energy due to its inability to get true absolute atomic energy ) = DFT is Not an ab-initio theory at all ( this p.10-second-paragraph ).
Of course, this one-pseudo-electron approximate DFT often failed to explain the actual multi-electron phenomena such as intermolecular energies ( this p.18-low ), metals ( this p.16-right ) and large molecules ( this p.2 ) due to lack of the universally-exact exchange-correlation pseudo-potential functional ( this p.17, this p.17-20, this p.13-upper, this p.2-first-paragraph ).
↑ Even the current most-widely-used emprical DFT hybrid exchange functional called B3LYP ( this p.8-1.5.4 ) often failed to give exact energies ( this p.3 ).
DFT has to artificially split one-pseudo-electron into multiple fictitious non-interacting subwavefunctions sharing only one electron's coordinate = r (= No physical meaning, this p.15 ) to mimic the ordinary molecular attractive constructively-interfering symmetric wavefunctions and Pauli repulsive destructively-interfering wavefunctions ( this p.12, this p.6, this p.34, this p.7 ).
If these fictitious DFT subwavefunctions can interact or interfere with each other like multi-electron wavefunctions, it causes paradoxical situation where some subwavefunctions cancel each other and vanish when there are more than two electrons.
As shown in the upper picture of Fig.10, when atom-A has an electron with spin-down, atom-B has an electron with spin-up. and atom-C has an electron with spin-up, all these three atoms-A,B and C must have the same positive-phase atomic wavefunctions to cause the constructive interference lowering kinetic energies or the molecular bond attractive exchange energies between the down-spin electron in atom-A and the up-spin electrons in atom-B and C.
But the Pauli repulsive antibond destructively-interfering exchange energy must be generated between two same up-up spins of atom-B and C, which means the atom-C's electron wavefunction must flip its phase to negative sign (= φC → -φC ), so the resultant positive and negative atom-C's wavefunctions cancel each other, and we cannot express the molecule consisting of three atoms with one down-spin and two up-spins, if these three wavefunctions are interacting (= not non-interacting ) with each other.
The fictitious non-interacting subwavefunctions cause serious problem in DFT's kinetic energy, which disproves the validity of DFT itself.
As shown in this, when there are only two electron (of two atoms ), only one molecular bond is formed between these two atoms, and all two electrons' density can concentrate on this single molecular bond formation like two hydrogen atomic wavefunctions are used for only one hydrogen molecular bond formation.
But when there are six electrons (or six atoms ), there are as many as 15 interatomic interactions between different combinations of these six electrons, hence, we have to split six electrons' charge density into 15 independent non-interacting subwavefunctions describing molecular attractive or Pauli repulsive exchange energies acting between these six electrons.
↑ So when there are only two electrons with two atoms, the single molecular bond between these two atoms can be strong enough by using all these two electrons' charges for its single molecular bond (= 2/1 ), but when there are six electrons, these six electrons' charges must split into 6/15 smaller charge for each interatomic interaction, which becomes far weaker than the case of two electrons.
↑ This means these DFT fictitious non-interacting subwavefunctions cannot generate enough interatomic exchange energies, when there are many electrons in the system considered, because the limited number of electrons' density must be divided into many noninteracting independent subwavefunctions for all possible different interatomic interactions among many electrons.
So after all. one-pseudo-DFT approximation also failed to express the quantum mechanical Pauli principle, which basically has the unavoidable fatal flaw especially in more than two electrons.
But this failed one-pseudo-electron DFT is the current only usable quantum mechanical approximate method even after physicists observe actual multiple atomic behavior using the atomic force microscopes ( this last ). Physicists often use various artificially-created pseudo-potential functionals and adjustable parameters for this useless DFT model ( this p.2-left, this p.5-right ).
Physicists artificially created various interatomic pseudo-potential energies such as Lennard-Jones potential containing empiriically-fitted parameters where Pauli repulsion cannot be obtained from the quantum mechanical theory ( this p.3-left-2nd-paragraph ).
As a result, all the ad-hoc quantum mechanical models such as valence bond, molecular orbital, and one-pseudo-electron DFT are unable to explain its unphysical Pauli principle's exchange energies, which fatal contradiction proves the quantum mechanics is definitely wrong.
(Fig.7) Four Helium atoms (= A,B,C,D ) are arranged tetrahedrally. ← Each unphysical molecular orbital ( in four He1, He2, He3, He4 molecular orbitals ) contains two electrons up and down spins: each electron must be unrealistically spreading all over four Helium atoms.
Here we show one typical example where the unphysical quantum mechanical molecular orbitals can neither remove unnecessary Pauli repulsion nor generate the necessary van der Waals attraction between four helium atoms (nor generate covalent sigma bond's energy in molecules with multiple atoms, this p.1-left-2nd-paragraph ), hence, quantum mechanics is inconsistent with the experimental results, and wrong.
In the upper figure, four helium atoms (= each of He-A, He-B, He-C, He-D atoms contains each helium 1s atomic orbital wavefunction φA, φB, φC, φD, respectively ) are arranged regular tetrahedrally (= distances between any two helium atoms are supposed to be equal, meaining all the overlap or exchange integrals (= S ) between any two of these helium atoms are also equal ).
Each atomic orbital contains one electron, which condition is called "normalization" expressed as the integral of two same atomic wavefunctions being 1 like
∫φAφA = ∫φBφB = ∫φCφC = ∫φDφD = 1
And the overlap (= or exchange ) integral between any two different helium atomic orbital wavefunctions becomes S due to the same interatomic distance between any two electrons ( this-(7) ) like
∫φAφB = ∫φAφC = ∫φAφD = ∫φBφC = ∫φBφD = ∫φCφD = S.
Four helium atoms contain the total eight electrons = four electrons with up spins and four electrons with down spins.
Due to the fatal flaws of quantum mechanical Pauli antisymmetric wavefunctions, any molecular bond attractive exchange energies between two different up and down spins become zero, and only unnecessary Pauli repulsive exchange energies between two electrons with the same up-up or down-down spins remain.
↑ To avoid this quantum catastrophe, quantum mechanical ad-hoc molecular orbital theory demands that any overlap or exchange integrals between any two different molecular orbitals must be zero, which artificial condition is called "orthogonal" or "orthonormal (= orthogonal + normalization, this p.14, this p.6 )."
Each molecular orbital can contain the maximum two electrons with up and down spins due to Pauli exclusion principle, so four different molecular orbitals (= He1, He2, He3, He4 ) are necessary to describe interactions between four helium atoms containing eight electrons (= two electrons with up and down spins × four molecular orbitals ).
Quantum mechanical molecular orbital is unrealistic, because each electron must always spread all over four helium atoms, and each electron's unphysical molecular orbital (= MO ) must be expressed as the linear combination of multiple (= four helium ) atomic orbitals (= AO, this middle-methane-case ).
Each molecular orbital contains one electrons, so the ( Coulomb ) integral of the same two molecular orbital (= total probability density of each electron ) must be 1, like
∫He1He1 = ∫He2He2 = ∫He3He3 = ∫He4He4 = 1
which normalization condition gives different normalization coefficients to different molecular orbitals.
As shown in the upper figure, we can find four (unphysical) molecular orbitals which are orthogonal to each other, which means the overlap integrals of any two different molecular orbitals must be zero like
∫He1He2 = ∫He1He3 = ∫He1He4 = ∫He2He3 = ∫He2He4 =
∫He3He4 = 0.
↑ But even if this artificial orthogonal molecular orbitals are created, quantum mechanical molecules cannot avoid unnecessary Pauli repulsive exchange energies between the same spins (= between four electrons with the same up spin of four helium atoms, and between four electrons with the same down spin of four helium atoms ), after all, so quantum mechanics is false.
Due to the orthogonal molecular orbitals (= any overlap or exchange integrals between any two different molecular orbitals are zero ), only ordinary Coulomb integrals (= integral of two same molecular orbitals ) remain, when we integrate the chosen wavefunctions with Schrodinger energy equation (= H ) to obtain (fake) total energy.
↑ But each molecular orbital is the linear combination of multiple different atomic orbitals, so the ordinary Coulomb integrals of the same molecular orbitals or the square (= probability ) of each molecular orbital automatically contain the exchange energy integrals.
The nomalization coefficients of Pauli repulsive antibond molecular orbital including the minus-phase atomic orbital tend to be bigger than the attractive molecular bond orbital including only the positive-phase (spatial) atomic orbitals.
So after all, the sum of the ordinary Coulomb integrals of four molecular orbitals gives the Pauli repulsive exchange energy integrals (= negative overlap or exchange integral = -S ) between the above four helium atoms.
It means the quantum mechnaical molecular orbitals can Not avoid unnecessary Pauli repulsive exchange energies, and cannot express the actual van der Waals attraction between helium atoms without adding artificial pseudo-potential energies. ← Quantum mechanics is proven wrong.
(Fig.8) The most-widely-used quantum mechanical DFT approximation tries to add artificially-chosen pseudo-potential or fictitious exchange energy consisting of only one pseudo-electron (= ρ(r) ) to seemingly fix the unnecessary Pauli repulsive energies caused by multi-electron molecular orbitals in vain.
All muti-electron quantum mechanical theories such as molecular orbitals failed to eliminate unnecessary Pauli repulsive exchange energies.
So physicists had No choice but to create the unrealistic quantum mechanical approximation called density functional theory (= DFT ) or Kohn-Sham theory which unreasonably replaced the whole many-electron material or molecule by just one pseudo-electron model (= unreal quasiparticle model, this p.3, this p.11-top ), which is allegedly moving in some unknown fictitious potential energies called exchange-correlation functionals ( this p.27 ).
Quantum mechanical Pauli exclusion principle must be expressed as unphysical antisymmetric wavefunctions or Slater determinants where exchanging any two electrons should give the same original wavefunction (= so each electron is indistinguishable and inseparable from other different electrons in different positions ) except for the sign flip.
↑ This quantum mechanical Pauli antisymmetric wavefunction or Slater determinant becomes canceled to be zero, when it contains only one electron like
antisymmetric wavefunction = φA(1)φB(2) - φA(2)φB(1) → φA(1)φB(1) - φA(1)φB(1) = 0 (= when it contains only one electron 1 = 2 ).
DFT uses only one pseudo-electron, it means if we apply this one-pseudo-electron of DFT to the multi-electron quantum mechanical Pauli antisymmetric wavefunctions, these wavefunctions vanish !
But even this one pseudo-electron DFT approximation is said to satisfy the same condition as the multi-electron quantum mechanical (useless) Pauli antisymmetric wavefunction or Slater determinants ( this p.2-3rd-paragraph ).
How does DFT using only one electron incorporate the multi-electron quantum mechanical Pauli principle without canceling its antisymmetric wavefunctions ?
As I said, the multi-electron quantum mechanical molecular orbital wavefunctions must be orthogonal to each other ( this p.1-lower ), which means any overlap or exchange (energy) integrals of any two different molecular orbitals must be zero ( this p.14 ), and only the sum of the Coulomb integrals of the same two wavefunctions or the square of the same wavefunctions remains as the total energy.
DFT artificially splits its one pseudo-electron (= ρ(r) ) into multiple fictitious non-interacting sub-wavefunctions squared (= all these split sub-wavefunctions keep sharing only one electron's coordinate r, this-3.2.1, this p.9 ) like
ρ(r) = φ1(r)2 + φ2(r)2 + φ3(r)2 + φ4(r)2
↑ These DFT fictitious artificially-chosen sub-wavefunctions sharing one electron coordinate correspond to the Coulomb integrals of the multi-electron quantum mechanical molecular orbitals.
In quantum mechanical unphysical Pauli antisymmetric wavefunctions, all electrons are unrealistically indistinguishable and inseparable (= as if all multiple different electrons hehave like one pseudo-electron ), so if their molecular orbitals are orthogonal, and only Coulomb integrals remain, it could be changed into one-pseudo-electron DFT model ( this p.30(or p.18)-footnote ).
Actually, these DFT fictitious sub-wavefunctions must be also orthogonal or orthonomal (= overlap or exchange energy integrals of two different sub-wavefunctions must become zero ) to each other ( this p.17, this p.10, this p.8-lower, this p.2-right-last ) like
∫φ1(r)φ2(r) = ∫φ1(r)φ3(r) = .. = 0
↑ It means these artificially-chosen DFT subwavefunctions must be the artificially-constructed orthogonal linear combinations of multiple atomic orbitals ( this p.3, this p.38, this-(1), this p.4-upper ) and always spread over all atoms (= hence, each electron and atom are unrealistically inseparable from other atomic electrons also in DFT ) like the ad-hoc molecular orbitals, as shown in the above case of the four helium atoms.
For example, as shown in the above figure, one DFT subwavefunction φ1(r) and another subwavefunction φ2(r) cancel a part of each other's terms, if DFT's one pseudo-electron can interact with each other like
φ1(r) + φ2(r) = ( φA + φB + φC + φD ) + ( φA + φB - φC - φD ) = 2( φA + φB ) ?
↑ This is why DFT fictitious electron must be non-interacting.
Non-interacting (= independent ) subwavefunctions mean, as the number of electrons in the system considered is larger, the number of interactions among those more electrons is larger, and they have to split the limited number of electron's density into more smaller independent interactions, so each interelectronic or interatomic interaction is weaker, as the electrons increase in DFT, which also disproves DFT and molecular orbital theory.
And these artificial orthogonal DFT subwavefunctions also contain unnecessary Pauli repulsive exchange energies inside their Coulomb integrals of orthogonal fictitious subwavefunctions (= ∫φ1(r)φ1(r) + φ2(r)φ2(r) + φ3(r)φ3(r) + φ4(r)φ4(r) contains unneeded Pauli repulsive exchange energies ) like the multi-electron molecular orbitals.
To eliminate these unnecessary Pauli repulsive exchange energies inherent in the orthogonal (sub-)wavefunctions, DFT rely on various artificially-created pseudo-potential energies called exchange-correlation functionals, which exact form is unknown or non-existent ( this 5th-paragraph, this p.20-lower, this p.6, this p.17 ).
These DFT pseudo-potential energies or exchange-correlation functionals basically consist only of one pseudo-electron density (= ρ(r) or n(r), this p.7-8, this p.7, this p.6,10~ ), hence, these ad-hoc DFT pseudo-potential energies cannot distinguish or separate each different electron or atom. ← DFT is inapplicable to actual nanotechnology which needs manipulation of different atoms and electrons separately.
Inside these DFT pseudo-potential energies or exchange functionals, all different electrons with spins must be treated as one big inseparable pseudo-electron (= DFT has No potential energies separating or distinguishing each different electron with differen spin, though distinguishing each different electron with different spin is indispensable to correctly estimate the attraction between different spins or repulsion between the same spins ).
Hence, these fictitious DFT exchange potential energies cannot be used to push, pull or separate different electrons or atoms. ← Quantum mechanical most-widely-used DFT approximation is completely useless and unable to describe actual multi-electron atomic bahaviors whose knowledge is necessary for developing useful nano-technology.
Furthermore, the quantum mechanical molecular method of artificially choosing either attraction expressed as spacial symmetric wavefunctions or Pauli repulsion expressed as antisymmetric wavefunctions is inherently unable to describe actual intermolecular interactions mixing van der Waals attraction and Pauli repulsion (= creating a mixed symmetric and antisymmetric spacial wavefunction is impossible ).
This is why DFT can Not explain intermolecular van der Waals interactions ( this p.1-failure, this p.3, this p.48, this p.63 ).
DFT tries to artificially create and add various ad-hoc pseudo-potential energies or exchange energy functionals by manipulating many free empirical parameters to explain van der Waals force in vain ( this p.3-4, this p.2, this p.2, this p.22 ).
↑ Despite this irreparable contradiction, the current physicists try to find the illusory universal DFT fictitious exchange potential energy functional consisting of only one inseparable pseudo-electron model, which should paradoxically describe any behaviors of arbitrary numbers of separable differnet electrons in vain.
↑ Finding this dreamlike still-unknown universal DFT pseudo-potential functional allegedly describing any multi-electron behaviors using only one-pseudo-electron model is definitely impossible ( this p.39-last-paragraph ).
As I said, each ad-hoc orthogonal subwavefunction must always spread all over different atoms, which also cannot separate different electrons or atoms inside multi-electron or multi-atomic materials.
So it is intrinsically impossible for the one-pseudo-electron DFT model to distinguish and separate different electrons (= if all electrons are unrealistically indistinguishable and inseparable, all atoms are also inseparable ), which means it is impossible to apply this one pseudo-electron DFT model to the actual multi-electron or multi-atomic materials or molecules.
But due to the quantum mechanical fatal flaws = unphysical Pauli antisymmetric wavefunctions, only one pseudo-electron DFT approximation with artificially-adjustable pseudo-potential energies remain as the calculation tool of (fake) molecular energies in all the current physics and chemistry.
So all the current atomic and applied science miserably stops progressing by these unrealistic and paradoxical quantum mechanical models such as the most-widely-used one inseparable pseudo-electron DFT approximation.
(Fig.9) Quantum mechanical materials, metals are unrealistic consisting of the unphysically spreading useless wave instead of real separable electrons.
Quantum mechanical most-widely-used one-pseudo-electron DFT or density functional theory is known to be unable to explain ordinary metals, semiconductors, strongly-correlation systems, band energy gap, and excited energies.
Also in these ordinary materials such as metals and semiconductors, the unphysical quantum mechanics and its leading model = DFT have to unscientifically treat all different electrons belonging to different atoms as one big inseparable pseudo-electron model (= denoted as ρ(r) or n(r) ) containing only one pseudo-electron's coordinate r.
So all quantum mechanical pseudo-models such as one-pseudo-electron DFT or Kohrn-Sham equation are unable to describe actual electric currents where each separable electron must be actually moving from one atom to another atom inside metals and semiconductors, which means the tired cliche "quantum mechanics was useful for developing modern computers is a total lie.
Actually, all quantum mechanics can do is describe the whole material or metal as an "unrealistic band" or the nonphysical spreading plane wave consisting of one pseudo-electron ( this p.1-(2), this p.24, this p.39 ) or fictitious quasiparticle with unreal effective mass (= which could be negative mass, this p.6, this-Table1 ) without giving any realistic pictures of individual separable electrons.
Due to unphysical Pauli antisymmetric wavefunction causing fictitious exchange energies, all quantum mechanical models cannot handle or distribute actually separable electrons into different atoms.
↑ It means quantum mechanics cannot describe the realistic situation like an electron-1 existing in an atom-A, while another electron-2 exists in an atom-B, instead, quantum mechanics says an electron-1 (or electron-2 ) must always exist in both different atoms-A and B simultaneously and unrealistically, which means we cannot separate an atom-A containing an electron-1 from an atom-B containing an electron-2, because the same single electron-1 (or electron-2 ) must always bridge these two atoms-A and B simultaneously.
Also in one-pseudo-electron DFT model, each electron must always spread over all atoms in the whole material as one unrealistically-inseparable fictitious electron (= ρ(r) or n(r) ) inside (pseudo-)potential energies and exchange-correlation energy functionals (= Exc ), which exact form is unknown (and non-existent ), but all the current physicists are pursuing it in vain.
In metals and semiconductors, DFT must artificially add another ad-hoc pseudo-potential (= another exchange and Coulomb) energy including freely-adjustable parameter U (= DFT+U ) to the original exchange-correlation energy functionals such as LDA,GGA,PBE.. (→ LDA+U, GGA+U..) in order to artificially deal with the material's strong Coulomb force effect ( this p.3 ).
↑ This means finding DFT's (non-existent and illusory) universal exchange-correlation energy functional allegedly applicable to all metals (= + U ) and non-metals (= U is unnecessary ) is impossible forever ( this p.7, this 7-6th-last paragraphs, this 2nd-paragraph ).
↑ These ad-hoc parameters U must be artificially changed and adjusted into different values in different materials or metals based on experimental results, and quantum mechanics has No power to predict all these energy parameters ( this p.1-left, this p.4-last-paragraph, this p.1-left-last-paragraph, this p.3 ).
Or physicists have to artificially choose (unreal) pseudo-potential energy ( this p.9-left-2nd-paragraph ) or additional perturbation energy (= λV, λ is freely-chosen parameter ) to manipulate total energy where there is No original quantum mechanical prediction ( this p.3-left-lower ).
The most serious irreparable problem of quantum mechanics and its leading model = one-pseudo-electron DFT approximation is they cannot separate different atoms or electrons, hence, their unphysical quantum models cannot use "real (measurable) forces" between atoms to know in which direction each atom will be moved by other external atomic forces, because of No real force allowed in Pauli exchange energies.
In metals, semiconductors and periodic crystals, DFT often aritificially chooses the abstract unphysical plane wave model spreading over all atoms with No real electron's shape (= expressed just as nonphysical spreading functions of eikr or simple sinusoidal curve, this p.16-33, this p.6-12 ) as one pseudo-electron wavefunction or basis set whose kinetic energies (= contained in the de Broglie wavelength ) or the upper energy's cut-off must be artificially adjusted ( this p.22,33, this p.6-right, this p.27-37 ).
↑ These very old quantum mechanical abstract (augmented) plane wave (= APW ) function allegedly representing the (pseudo-)electron model has been amazingly unchanged (= stopped progressing ) and used even now ( this p.9-left ), since it was first invented by Slater in 1937 ( this p.3-47 ). ← This proves our atomic science has made No progress for a long time.
↑ So this plane-wave-shaped electron unrealistically spreading over all different atoms inside materials cannot be divided into different individual electrons belonging to different atoms, which quantum mechanical model cannot be utilized for any practical purpose which needs to move each different atoms (= containing different separable electrons ) separately.
Each electron in quantum mechanical material or metal is often expressed as the (artificially-chosen) spreading plane wave function in the interstitial region (= all place except for near each atomic core ) + atomic (sphere) wavefunction only around each atomic core, which ad-hoc separation methods or parameters must be artificially determined differently in each different materials using abstract nonphysical models, various pseudo-potentials ( this p.11-12, this p.68-69, this p.9 ) and unreal electron's effective masses ( this p.3,14 ).
All these unphysical pseudo-electron's plane wave or DFT's fictitious non-interacting sub-wavefunctions must obey the unscientific quantum mechanical rule = orthogonal wavefunctions where any overlap integrals of two different plane waves must be zero. ← This quantum mechanical meaningless restriction is one of main reasons why quantum mechanical electron wave functions have remained impractical and unchanged for a long time.
As I said, for atoms and electrons to be used for really useful purposes, each different atom with concrete shape (= given by different electrons existing in different atoms ) must be moved separately from other atoms using "real forces (= instead of unphysical exchange energies lacking real physical forces )", which means electrons in one atom also must be separable from other electrons in other atoms, which basic separation is impossible in the unphysical quantum mechanical Pauli antisymmetric wavefunctions or exchange energies.
So in any molecules and materials such as metals, semiconductors and insulators, quantum mechanics is intrinsically unable to describe actually-separable and movable electrons, hence completely useless, and preventing our scientific development forever.
The important point is that quantum mechanics can Not predict or explain any intermolecular energy necessary for protein-protein enzymatic reactions such as Pauli repulsion and van der Waals attraction called London dispersion , so quantum mechanics is intrinsically false.
Intermolecular attraction called van der Waals potential is known to be inversely proportional to the intermolecular distance (= r ) to the 6th power (= - C6/r6 ).
Quantum mechanical wavefunctions can only generate intermolecular potential proportional to gentler exponential function (= e-r/r ), which completely disagrees with actual van der Waals attractive potential (= 1/r6 ).
So the contradictory quantum mechanics has to give up calculating the denominator part of the inverse 6th power, and tries to paradoxically focus only on artificially adjusting and fitting the numerator parameter C6 to experimental value empirically with No power of prediction.
Also in their (fake) ab-inito method, quantum mechanics can only deal with and manipulate the numerator parameter C6 (= called dispersion coefficient ) or electric polarizing parameter α (called polarizability ) by using unreal concept called imaginary frequency (= iω, this p.13-18, p.22-24, this p.2-5, this p.45 ) and artificially choosing (fake) basis wavefunction to fit experimental results ( this p.9-11-(32)(33), this p.4-right-1st-paragraph ).
↑ In this manipulation of van der Waals parameter C6 or fictitious polarizabilities α consisting of unreal imaginary frequency, the coupled cluster (= CC ) method's artificially chosen wavefunctions are often used ( this p.1-4, this p.1-4 ) as "gold standard", but his CC (or CCSD ), which is known to be Not variational method, which means CC often gets wrong energies lower than the experimental energies ( this p.1-left-1st-paragraph, this 1st-paragraph ). ← so CC is false.
↑ Furthermore, all these quantum mechanical ad-hoc methods often cause wrong intermolecular energies called basis set superposition error (= BSSE ) which must be artificially corrected by adding imaginary Ghost atoms. ← No prediction by quantum mechanics ( this p.5-Table I, this p.19-lower ).
Quantum mechanical wavefunction changing exponentially (= e-r/r r is intermolecular distance ) is also unable to explain intermolecular Pauli repulsion, which is much more steeply changing proportional to C12/r12 = the 12th power of intermolecular distance ( this p.2-right, this p.11, this p.19-1st-paragraph ), which must be explained by empirically-fitting Lennad Jones potential ( this p.3-2nd-paragraph, this p.2-right-last-paragraph ) based on experiments Not on quantum mechanical theory.
There are some ad-hoc Pauli repulsive potentials artificially created to change exponentially (ex. Buckingham or Born-Mayer potential ) mimicking quantum mechanical original wavefunction's exponential change.
↑ But this exponentially-changing artificial Pauli repulsive potential (= like quantum mechanical Pauli repulsion ) can Not cancel the van der Waals attraction decreasing more acutely obeying -1/r6 ( this p.4-2nd-paragraph ), so false ( this p.2-left-1st-paragraph, this p.4-left-1st-paragraph ).
↑ This useless quantum mechanics has to unphysically decompose the total intermolecular energy into van der Waals dispersion energy, Pauli repulsive energy, Coulomb energy.. and choose ad-hoc independent different pseudo-potentials and free parameters for these decomposed different energy terms, which (fake) ab-initio method can Not predict any energy values ( this p.3-2nd-paragraph, this p.1-intro ).
The current most-widely used quantum mechanical approximation called density functional theory (= DFT ) is also unable to explain or predict any intermolecular dispersion interaction ( this p.1-left ), so DFT has to artificially create and choose fictitious intermolecular potentials whose parameters must be empirically fitted to experiments ( this p.8-left, this p.1-right-upper ) using ad-hoc damping function ( this p.2, this p.5-left ), in addition to its fictitious exchange correlation functionals ( this p.3-adjustment ).
Originally, quantum mechanical Pauli principle has fatal defects which can Not deal with atoms or molecules with more than two electrons mixing singlet (= symmetric spatial wavefunction ) and triplet (= antisymmetric spatial wavefunction ).
So quantum mechanics unreasonably discarded only the singlet symmetric spatial wavefunction and leaves only Pauli repulsive (triplet) antisymmetric spatial wavefunction expressed as Slater determinant in generalized cases of more than two electrons.
↑ This means quantum mechanical contradictory Pauli principle tends to generate excessive Pauli repulsion, and can Not generate van der Waals attraction nor covalent bonds connecting many electrons.
This is one of fatal defects of quantum mechanics.
Considering unrealistic quantum mechanical parallel worlds and relativistic paradoxes, it is natural to think the "actually-tangible" Pauli repulsive contact force is caused by some "real substance" or medium (= because we can actually touch and feel this Pauli repulsion ! So there is some real substance there ! ) generating electron's de Broglie wave interference, which has No contradiction and presents more realistic explanation than quantum mechanical wavefunction or de Broglie wave destructive interference paradoxically increasing kinetic energy ( this 9th-sentence ).
Feel free to link to this site.
