Top page (correct new Bohr model, and quantum mechanics is wrong )
Strange "spin" is NOT a real thing
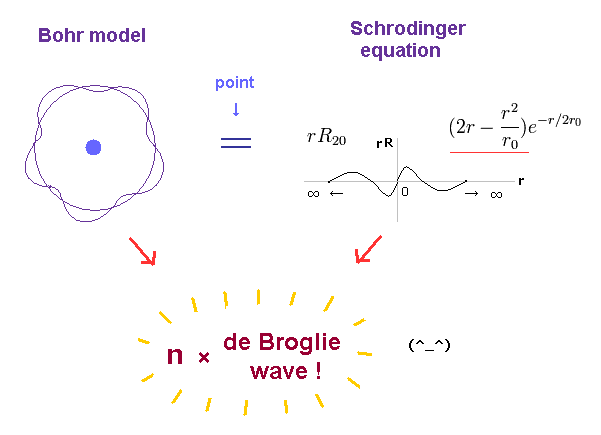
(Fig.1) Both Bohr model and Schrödinger equation obey the atomic orbital length equal to n × de Broglie wavelength.

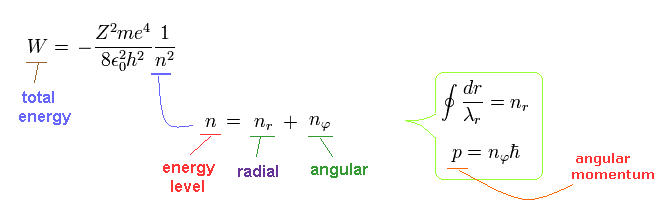
Realistic Bohr's atomic model successfully explained all energy levels of hydrogen-like atoms and ions including the small energy splitting called fine structure.
Bohr atomic model requires that an atomic orbital length should be equal to an integer (= n ) times de Broglie wavelength to avoid the experimentally-confirmed destructive interference (= of de Broglie wave ) to prevent electron's orbits from being unstable ( this p.4-last ).
↑ So the false explanation that Bohr atomic model may be unstable radiating energies ( according only to the older classical electromagnec theory excluding de Broglie wave ) was wrong and fabricated later to justify the unrealistic quantum mechanics, as seen in the fact that the realistic Bohr's atomic model was accepted by the then physicists and received the most prestigious Nobel prize as the legitimate atomic theory.
Electron de Broglie wavelength was confirmed in many experiments, so de Broglie wave was officially proved to be a real wave ( this p.2-3 ). = So we have to consider the destructive interference between de Broglie waves also in multi-electron atoms.
Quantum mechanical Schrödinger equation also used this de Broglie wavelength condition that its orbital length is quantized as an integer times de Broglie wavelength ( this p.2, this p.1-lower, this p.3-upper ), and obtained the same energy values as Bohr model.
But quantum mechanical Schrödinger equations have to include the unrealistic zero orbital angular molentum where an electron in s orbital must always crash into a nucleus and become unstable due to the destructive interference of the electron's de Broglie wave moving in the linear s-orbital (= zero angular momentum is like the earth crashes into the Sun in an unrealistic linear orbit )
So quantum mechanics is wrong, and only realistic Bohr atomic model can be extended to all other multi-electron atoms and molecules using the power of the modern computers ( = which modern computers didn't exist in 1920s, and this is why unreal quantum mechanics had to be accepted instead of realistic Bohr model ).
(Fig.2) From "circular" Bohr model to "elliptical" Sommerfeld model.
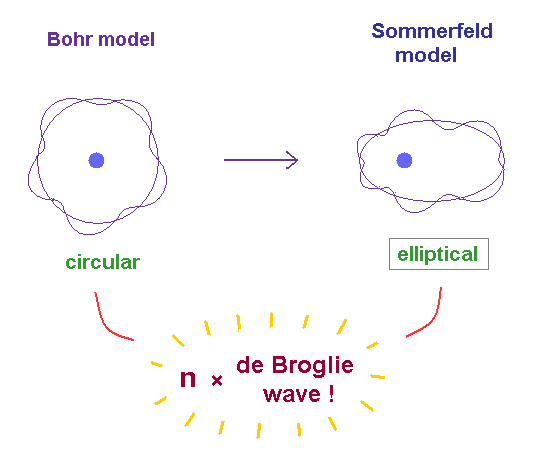
In 1916, Arnold Sommerfeld successfully extended Bohr's circular orbits to "elliptical" orbits which can include various different angular momentums in the same energy levels designated by the principal quantum number n (= an elliptical or circular orbital length is equal to n × de Broglie wavelength ).
Sommerfeld elliptical orbit also satisfies the quantized angular momentum ( this p.4-5, this p.2-3, this p.8 ) which means the elliptical orbital length should be equal to an integer number of de Broglie wavelength.
This condition is expressed as Sommerfeld quantization rule in both radial and angular directions, as shown on this site (p.119) and this site (p.3).
See this section in the detailed method of calculating energy levels in Bohr-Sommerfeld elliptical orbits.
(Fig.3) n × de Broglie wavelength in Bohr-Sommerfeld quantization.
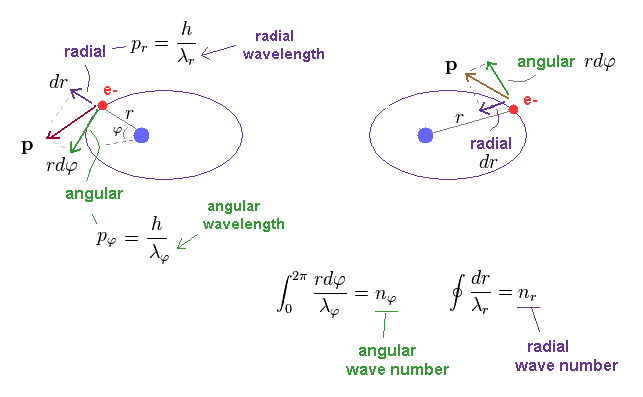
where "r" is radius, and φ is azimuthal angle.
Unlike the simple circular Bohr's orbit, elliptical orbit contains movement in "radial" directions.
We can separate each momentum at each point into angular (= tangential ) and radial components, which are perpendicular to each other.
"Perpendicular" means these two components are independent from each other.
So we need to calculate de Broglie waves in these two directions independently.
Numbers (= n ) of de Broglie wavelength in each tangential and radial directions are given by dividing one orbital length in each direction by each de Broglie wavelength (= λ ).
(Fig.4) n × de Broglie wavelength is separated into angular and radial parts.
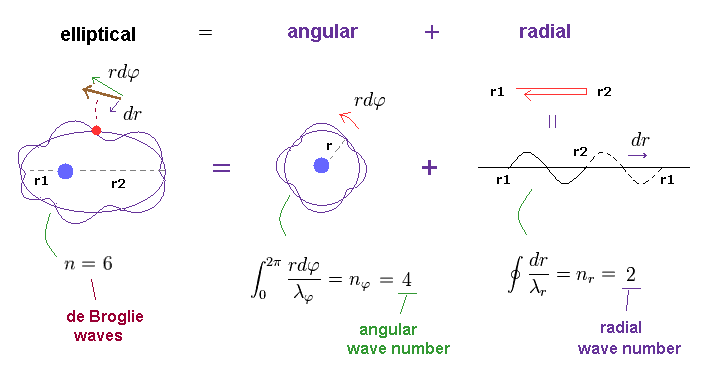
When the circumference of elliptical orbit ( this p.10 ) is n × de Broglie wavelemgth, this integer "n" can be expressed as the sum of angular and radial waves. See also this section.
In Fig.4, n is equal to "6", which is also equal to principal quantum number.
The whole path in tangential (= angular or azimuthal-angle direction ) direction is nφ (= 4 ) × λφ (= tangnetial de Broglie wavelength ).
And the radial path is equal to nr (= 2 ) × λr (= radial de Broglie wavelength ).
This is Sommerfeld quantization rule in radial and angular directions.
(Fig.5) Simple circular orbit = Only tangential (= angular ) movement.
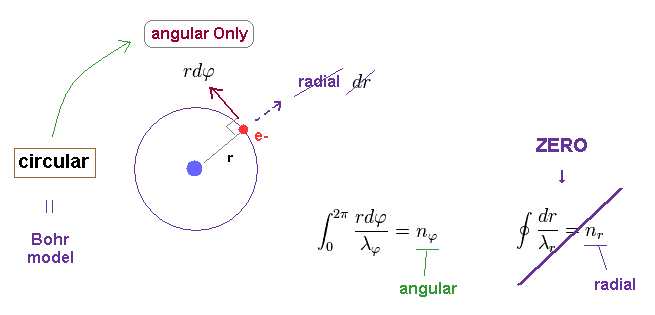
As shown in Fig.5, when an electron is moving in circular orbit, it moves Only in tangential (= angular ) direction.
So in circular orbit, the concept of radial momentum and de Broglie wavelength do NOT exist.
So the orbital length becomes n (= nφ ) × tangential de Broglie wavelength.
The original simplest Bohr model didn't think about the radial wave quantization, unlike Sommerfeld's elliptical orbit.
(Fig.6) n (= nφ ) × angular de Broglie wavelength.

In Fig.6, the circumference of this circular orbit is 5 × de Broglie wavelength.
( So, the principal quantum number expressing this orbital energy is "5", too. About the calculation, see this section. )
This is a circular orbit, so all these "5" de Broglie waves are in tangential (= angular ) direction.
"Radial" momentum and waves are NOT included in the completely-circular orbit at all.
(Fig.7) Schrodinger's hydrogen also consists of radial and angular parts.
Schrodinger equation also depends on an integer number of de Broglie wavelength in radial and angular directions.
See this site and this site. ( "node" is related to radial waves. )
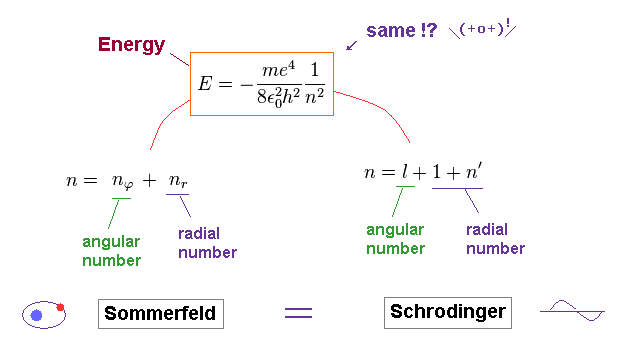
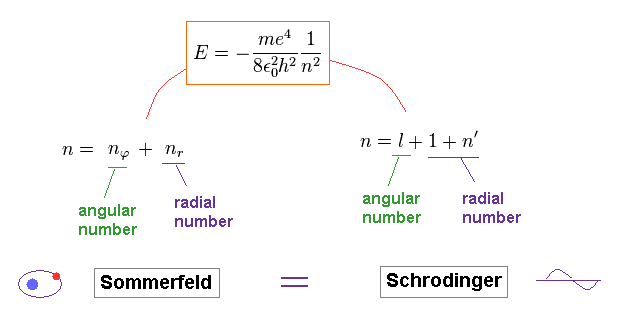
Comparing the energies of Bohr model and Schrodinger equation, they are just consistent with each other.
And the principal quantum number "n" is the sum of radial and angular ( wave ) numbers in both models.
(Fig.8) 1s wavefuntion = 1 × wavelength. 2s = 2 × wavelength.
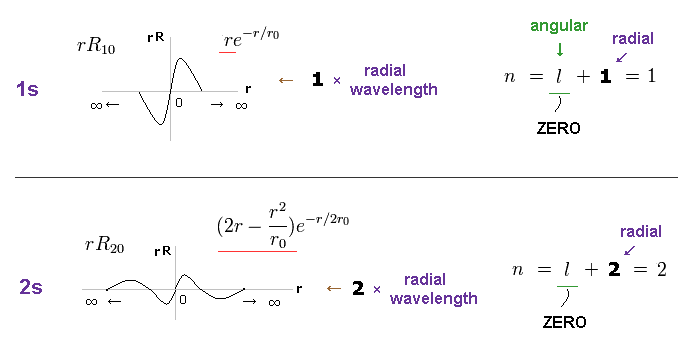
As shown on this site, Schrodinger wavefunctions of 1s and 2s orbitals become like Fig.8.
Radial wavefunction of χ = "rR" obeys de Broglie relation, as shown in Eq.1 and this section.
One orbit means the circumference from a point to the same point.
In Fig.8, from r = ∞ (= start ) to r = ∞ (= end ), 1s wavefunction contains 1 × de Broglie wavelength.
And 2s wavefunction contains 2 × de Broglie wavelength.
Neither 1s nor 2s has angular parts, so the angular quantum number l is zero.
(Eq.1) Schrodinger (radial ) equation for hydrogen atom.

In the latter part of this site, there are some examples of this radial amplitude of χ = rR.
The radial wavefunction of 2p orbital is 1 × de Broglie wavelength like 1s orbital.
But 2p also has angular wavefunction with quantum number l = 1.
The principal quantum number n is the sum of radial and angular wave numbers.
So 2p has n = 1 ( angular ) + 1 ( radial ) = 2 energy level like 2s orbital.
(Fig.9) 2p wavefunction: n = 1 ( angular ) + 1 ( radial ) = 2.
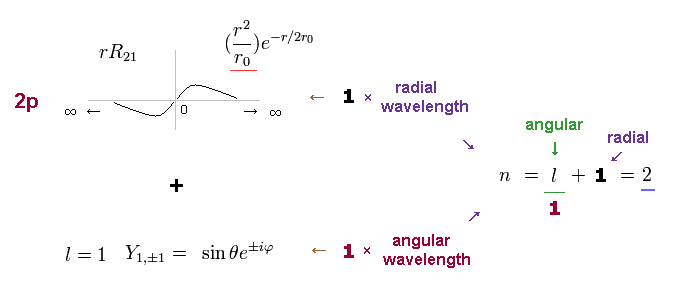
If you check hydrogen wavefunction based on Schrodinger equation in some websites or textbooks, you will find 1s radial wavefunction like Fig.10.
rR12 shows 1/2 de Broglie wavelength (= Fig.10 right ), so one orbit ( ∞ → 0 → ∞ ) includes 1 × de Broglie wavelength in the radial direction, as shown in Fig.8 upper.
(Fig.10) 1s hydrogen wavefunction = 1 × de Broglie wavelength.

As shown in this site and this site, Sommerfeld quantization conditions ( this p.7, this p.8 ) are
(Eq.2) Sommerfeld quantization.
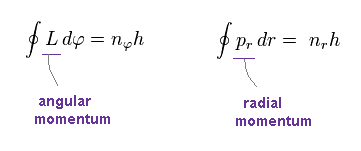
L is angular momentum, which is constant.
φ is azimuthal angle in the plane of the orbit.
pr is radial momentum of the electron.
h, nφ, nr are Planck constant, angular, and radial quantum numbers, respectively.
(Eq.3) Sommerfeld quantization = an integer × de Broglie wavelength.
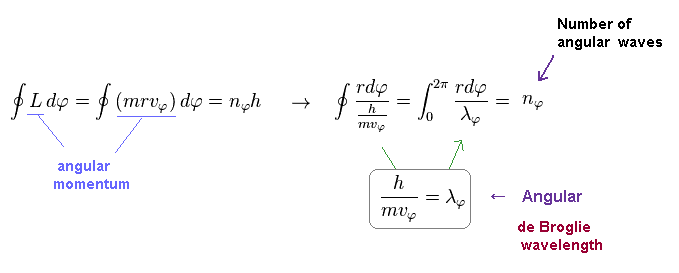
Using Eq.2 and de Broglie relation ( λ = h/mv ), you find condition of Eq.2 means an integer times de Broglie wavelength (= nφ × λφ ) is contained in the orbit in tangential direction.
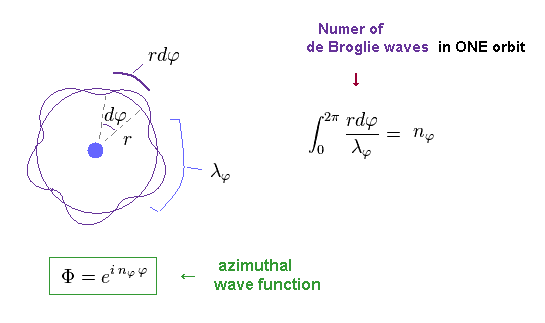
(Fig.11) Number of de Broglie wavelength in tangential direction.
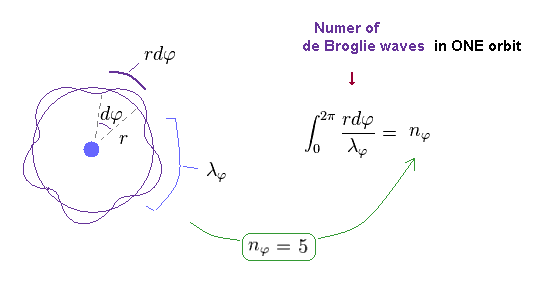
For example, in Fig.11, one orbit in tangential direction contains 5 × de Broglie wavelength.
Of course, this wavelength (= λφ ) is based Only on tangential momentum ( λφ = h / pφ ).
(Fig.12) Sommerfeld radial quantization. → nr × de Broglie wavelength !

Radial quantization condition of Eq.2 also means an integer times de Broglie wavelength is contained in one orbit in radial direction.
So Sommerfeld quantization conditions of Eq.2 require quantization in both radial and angular directions.
(Fig.13) Electron's movement in "radial" and "angular" directions.
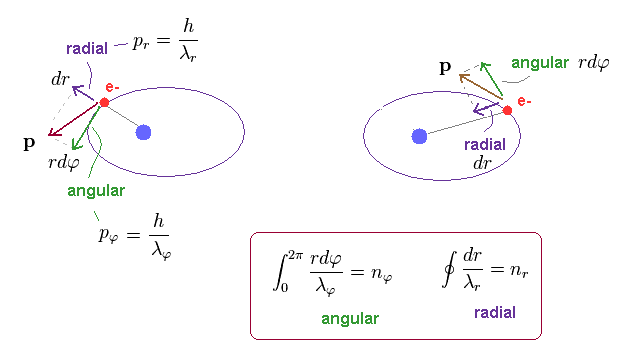
In elliptical orbit, the electron is moving both in angular and radial directions, as shown in Fig.13.
Using Pythagorean theorem, we can divide total momentum "p" into radial (= pr ) and tangential (= pφ ) components at each point.
These two directions are perpendicular to each other at each point.
So, radial (= λr ) and angular (= λφ ) de Broglie waves are independent from each other.
(Fig.14)
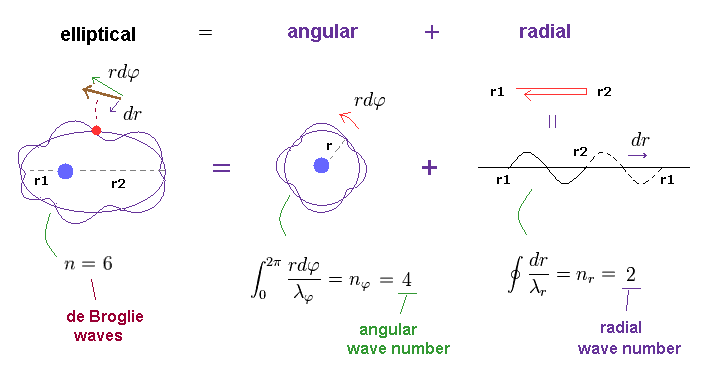
As shown in this section, total number (= n ) of de Broglie waves can be expressed as the sum of angular (= nφ ) and radial (= nr ) de Broglie waves.
In Fig.14 orbit, the principal quantum number n = 6, which also expresses total number of de Broglie wavelength.
Angular and radial quantum numbers (= wave numbers in each direction ) are "4" and "2", respectively.
So, the relation of n = 6 = 4 + 2 holds.
(Fig.15) Schrodinger's radial wavefunction is a integer de Broglie wavelength = Sommerfeld.
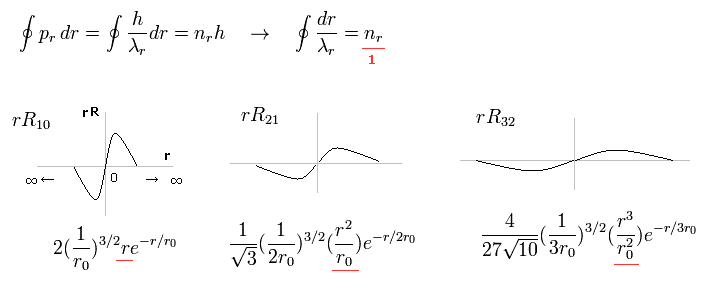
Fig.15 shows the examples of Schrodinger's wavefunctions including one de Broglie wavelength in radial direction of one orbit.
( One orbit means from one point to the same point, ∞ → 0 → ∞ )
For example, R32 wavefunction is "3" principal number ( n = 3 ) and "2" angular (= tangential ) momentum ( l = 2 ). So the radial wave's number is 3-2= 1.
These wave's numbers have the same meaning as Bohr-Sommerfeld model, which also has an integer de Broglie waves.
(Fig.16) Schrodinger's radial wavefunction, two or three waves.
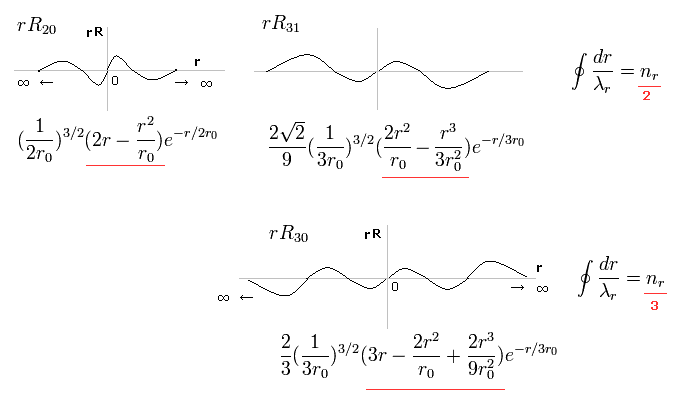
In the upper line of Fig.16, the radial one-round orbits are just two de Broglie wavelength.
For example, in R31, the principal quantum number is "3" and the angular momentum (= tangential ) is "1".
As a result, the radial wave becomes 3-1 = 2.
And in the lower wavefunction, n = 3 and l = 0, so the radial wave is 3-0 = 3.
(Fig.17) Schrodinger's tangential wavefunction (= angular momentum ) = Sommerfeld model.
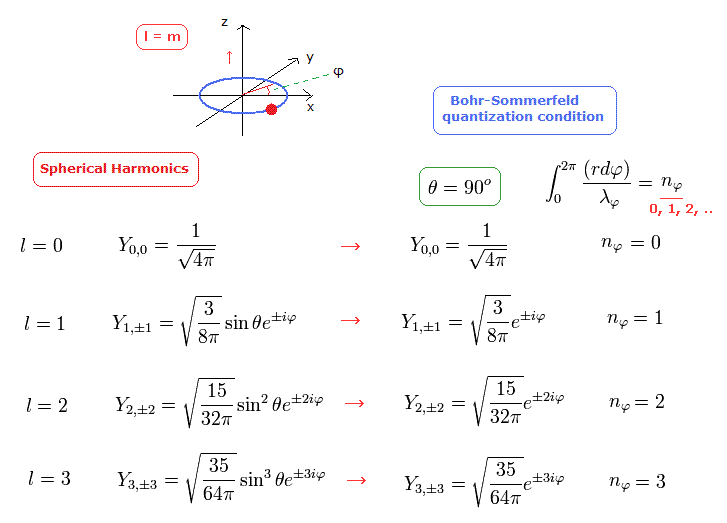
In Fig.17, the angular moementum of Spherical Harmonics in Schrodinger's hydrogen shows the tangential de Broglie wave's number in one orbit ( this p.16 ).
For example, in e2iφ = cos2φ + isin2φ, one round is two de Broglie wavelength. See this section.
Because the rotation by π returns its phase to the original one.
As a result, the total number of radial and tangential de Broglie waves means the principal quantum number ( n = energy levels ), in both Bohr-Sommerfeld and Schrodinger's models.
(Fig.18) Negative kinetic energy is unreal.
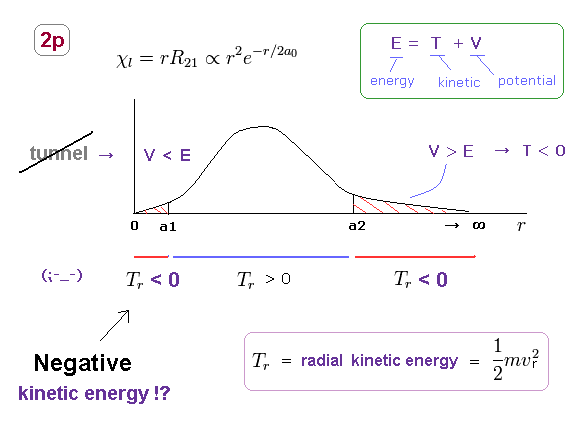
Unrealistically, the radial region of all orbitals in Schrodinger's hydrogen must be from 0 to infinity.
Fig.18 shows 2p orbital of Schrodinger's hydrogen.
In 2p orbitals, radial kinetic energy becomes negative in two regions ( r < a1, a2 < r )
Of course, in this real world, kinetic energy (= 1/2mv2 ) cannot be negative, which means Schrodinger's hydrogen is unreal.
In the area of r < a1, potential energy V is lower than total energy E, so, tunnel effect has Nothing to do with this 2p orbital.
Furthermore, it is impossible for the bound-state electron to go away to infinity ( and then, return ! ) in all stable atoms and molecules.
(Fig.19) "Elliptical" orbit (angular momentum = 1).
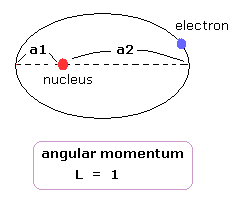
Here we think about the classial elliptical orbit with angular momentum = 1, like 2p orbital.
The distance between the perihelion ( aphelion ) and nucleus is a1 ( a2 ).
In classical orbit, when the electron has angular momentum, it cannot come closer to nucleus than perihelion (= a1 ).
(Eq.4)
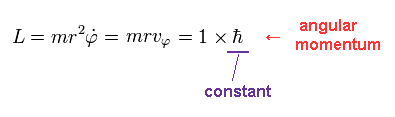
We suppose the angular momentum (= L ) of this orbit is ħ, which is constant.
Using Eq.4, tangential kinetic energy (= Tφ ) becomes
(Fig.20) Tangential kinetic energy becomes divergent as r → 0.
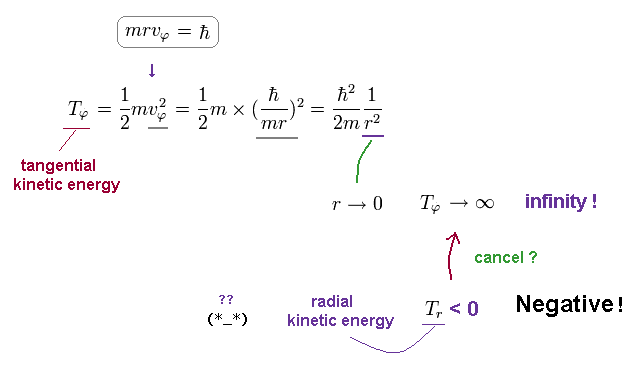
As shown in Fig.20, this tangential kinetic energy diverges to infinity, as r is closer to zero.
This Tφ is the inverse of r2, which cannot be cancelled by Coulomb energy (= -1/r ).
So, to cancel this divergence of tangential kinetic energy, radial kientic energy must be negative !
Unfortunately, our Nature does NOT depend on this artificial rule, so Schrodinger equation is unreasonable.
(Fig.21) Picking up only realistic region from a1 to a2 → "discontinuous" radial wavefuction.
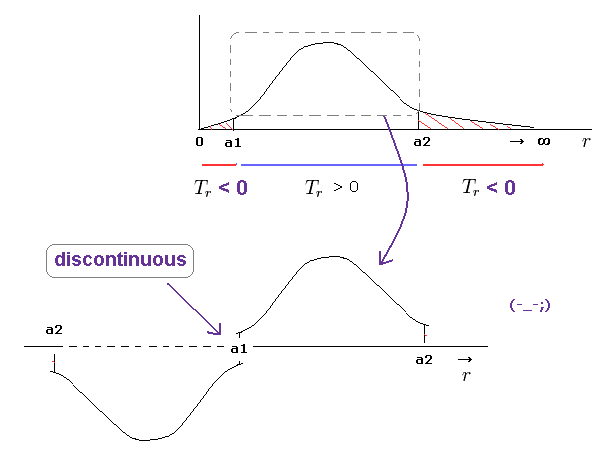
Some people may think we can pick up only realistic region ( a1 < r < a2 ) with positive kinetic energy from radial wavefucntion.
But it is impossible, because this wavefunction becomes discontinuous at a1 and a2 in this case.
One orbit means the electron must U-turn at a1 and a2, and returns to the original point.
(Fig.22) Discontinuous → Schrodinger equation does NOT hold.
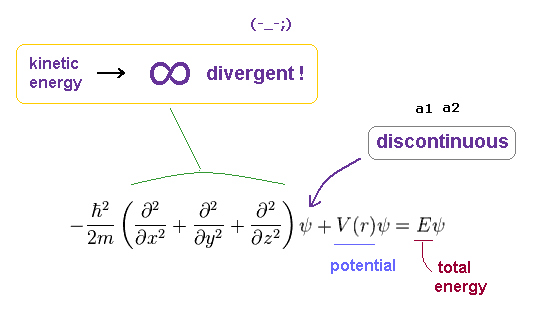
As a result, the discontinuous wavefunction of Fig.21 cannot hold in Schrodinger equation for hydrogen.
Because "discontinuous" means the gradient (= derivative ) of this wavefunction becomes divergent to infiniy.
At the points of a1 and a2, potential energy V and total energy E must be finite.
So sudden U-turn at these points makes this radial wavefunction unrelated to the original equation.
(Fig.23) Schrodinger's 2p radial wavefunction. Unreal "negative" kinetic energy.
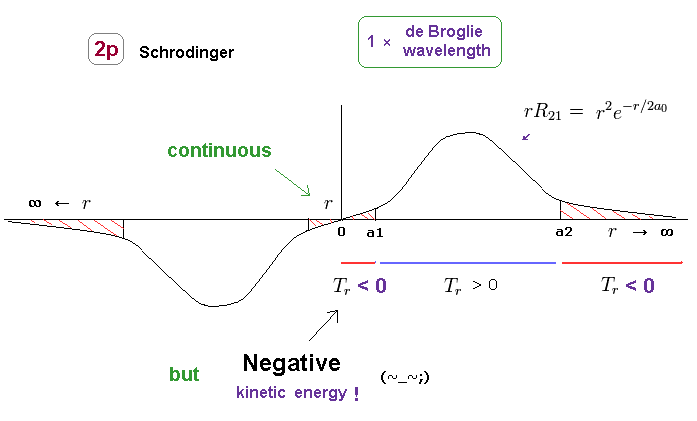
As shown in Fig.23, the original 2p radial wavefunction is continuous at both ends of r = 0 and ∞
Because the gradient and amplitude of the wavefunction becomes zero at these points.
Instead, this wavefunction must contain unrealistic region with negative kinetic energy.
As I said in Fig.18, this region has Nothing to do with tunnel effect.
(Eq.5) Schrodinger's radial equation for hydrogen.
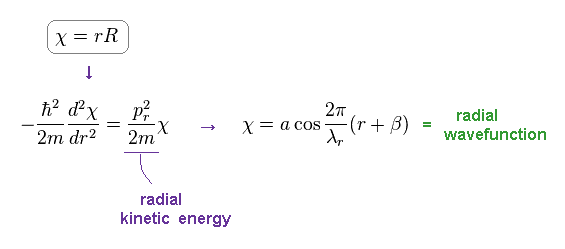
As shown on this site ( this p.3, this ), they replace the radial parts by χ = rR to satisfy de Broglie relation.
As shown in Eq.5, this wavefunction becomes cosine ( or sine ) functions with some wavelength λr.
(Eq.6) de Broglie relation holds in radial direction.

As a result, Schrodinger equation gives de Broglie relation ( radial momentum pr = h/λr ).
Here λr is radial de Broglie wavelength.
(Eq.7) Sommerfeld + de Broglie relation = Schrodinger equation.

Using Eq.6, Sommerfeld quantization condition of Eq.2 becomes like Eq.7.
Eq.7 shows number of ( radial ) de Broglie wavelength in the whole radial path becomes "nr".
This means Schrodinger's hydrogen also satisfies an integer times de Broglie wavelength like Bohr model !
(Fig.24) 2p radial wavefunction consists of different wavelengths.
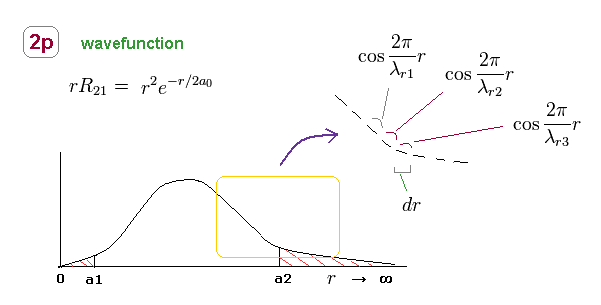
Like in elliptical orbit, radial momentum (= wavelength ) is changing at different points.
So, 2p radial wavefunction consists of infinite kinds of de Broglie wavelengths, as shown in Fig.24.
Within each small segment (= dr ), we can consider the de Broglie wavelength is a constant value.
(Fig.25) Quantization of radial wavelength.
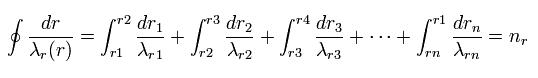
As a result, using different wavelengths (= λr ) at different points, Sommerfeld quantization condition in one orbit can be expressed lie Fig.25.
(Eq.8) Azimuthal Schrodinger equation.
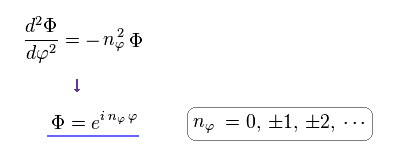
Eq.8 is azimuthal Schrodinger equation and wavefunction (= Φ ).
In this section, we show this quantized azimuthal wavefunction means an integer times ( tangential ) de Broglie wavelength.
(Eq.9) Schrodinger's azimuthal wavefunction = nφ × de Broglie wavelength.
Applying usual momentum operator ( in tangential direction ) to this azimuthal wavefunction (= Φ ), we obtain the tangential momentum (= pφ ), as follows,
(Eq.10)
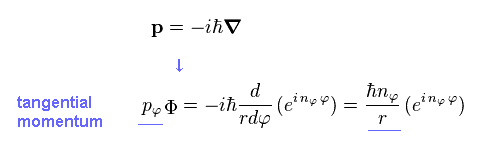
Using de Broglie relation, tangential de Broglie wavelength (= λφ ) becomes
(Eq.11)
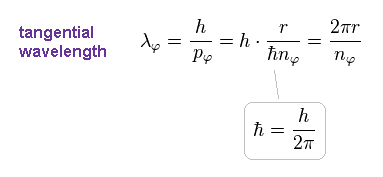
Here ħ = h/2π ( h is Planck constant ) is used.
Using Eq.11, the number of de Broglie wavelength in one ( tangential ) orbit becomes
(Eq.12)
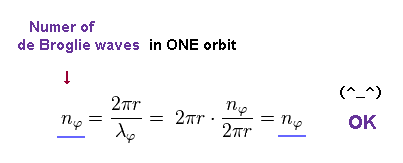
This equation holds true.
As a result, the azimuthal wavefunction of Eq.8 also means an integer number of de Broglie wavelength like Sommerfeld model.
(Fig.25) Bohr-Sommerfeld model.
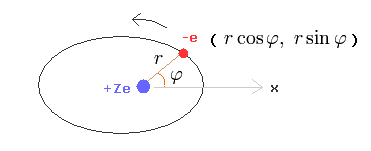
In this section, we actually calculate Bohr-Sommerfeld elliptical orbital energies of a hydrogen-like atom in detail ( this p.11-18, this p.8-12, this p.7-10 ).
This detailed calculation method is based on Sommerfeld's original paper in 1916 ( Annalen der Physik [4] 51, 1-167 ).
Here we suppose one electron is orbiting (= rotating or oscillating ) around +Ze nucleus.
( Of course, also in the Schrodinger equation of hydrogen, one electron is moving around +Ze nucleus by the Coulomb force. )
Change the rectanglar coordinates into the polar coordinates as follows,
(Eq.13)
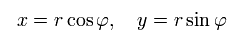
When the nucleus is at the origin and interacts with an electron through Coulomb force, the equation of the electron's motion becomes
(Eq.14)
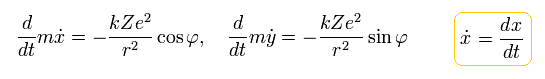
Here we define as follows,
(Eq.15) p = "constant" angular momentum.

Only in this section, we use "p" as
If one electron is moving around one central positive charge, this angular momentum ( = p ) is always constant and conserved (= law of constant areal velocity).
The coordinate r is a function of φ, so using Eq.15, we can express the differentiation with respect to t (=time) as follows;
(Eq.16)
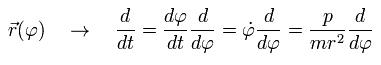
Here we define
(Eq.17)
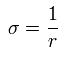
Using Eq.13 and Eq.16, each momentum can be expressed by,
(Eq.18)
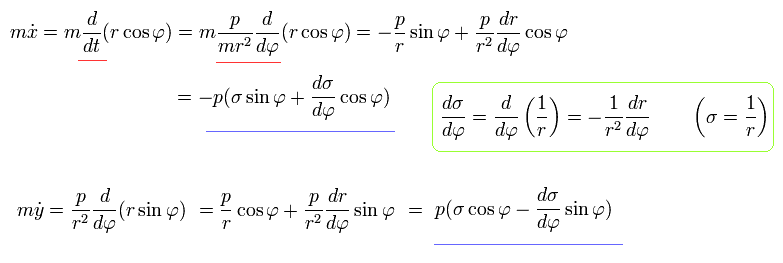
Using Eq.14, Eq.16, and Eq.18, the equation of motion becomes,
(Eq.19)
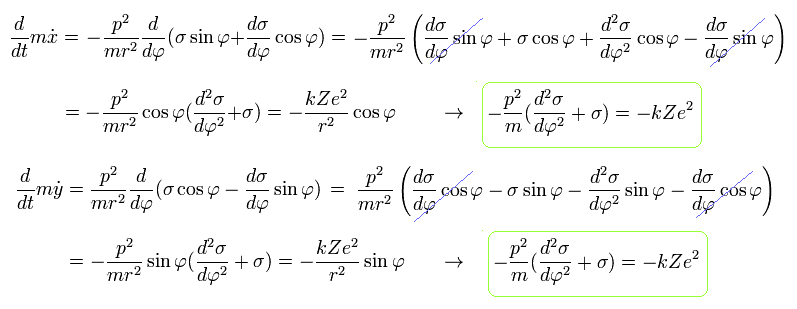
From Eq.19, we obtain the same result of
(Eq.20)
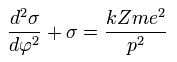
The solution of this σ in Eq.20 becomes,
(Eq.21)
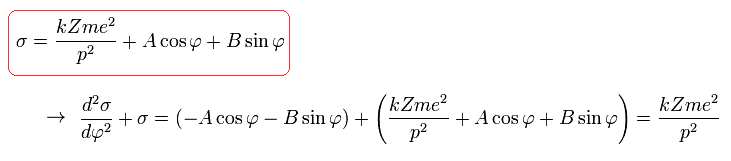
where we suppose that the electron is at the perihelion (=closest point), when φ is zero, as follows,
(Eq.22)
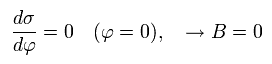
From Eq.17, Eq.21 and Eq.22, we find this electron's orbit is similar to the earth orbiting around the Sun obeying Kepler's law ( this p.1-(2) ) where the central Sun (= nucleus ) exists at the focus of the elliptical orbit.
(Fig.26) "Elliptical" orbit of hydrogen-like atom.
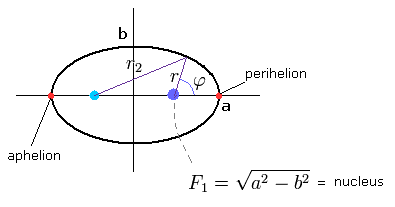
where the nucleus is at the focus (F1), and eccentricity (=ε) is,
(Eq.23)
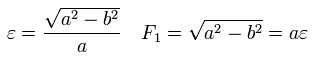
Here we prove the equation of Eq.21 ( B=0 ) means an ellipse with the nucleus at its focus.
Using the theorem of cosines in Fig.26, and from the definition of the ellipse,
(Eq.24)
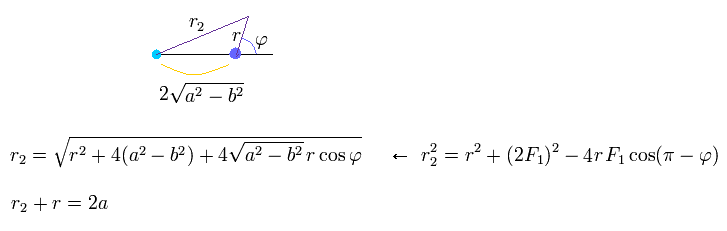
From Eq.24, we obtain
(Eq.25)
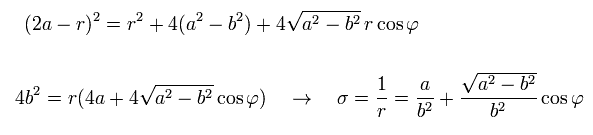
From Eq.21, Eq.22, and Eq.25, we have
(Eq.26)
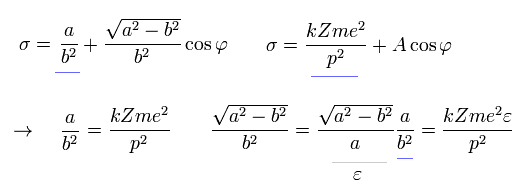
As a result, σ becomes,
(Eq.27)
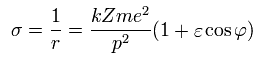
Using Eq.16 and Eq.27,
(Eq.28)
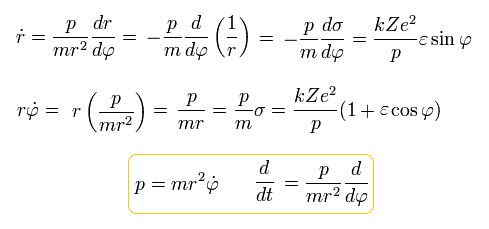
So the kinetic energy (T) becomes,
(Eq.29)
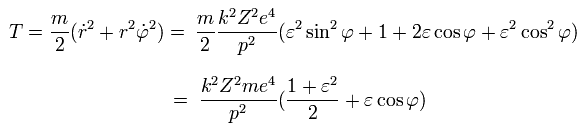
From Eq.27, the potential energy (V) is,
(Eq.30)
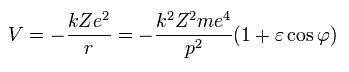
So the total energy (W) is,
(Eq.31)
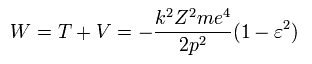
In the Bohr-Sommerfeld quantization condition ( this p.10-11 ), the following relations are used,
(Eq.32)
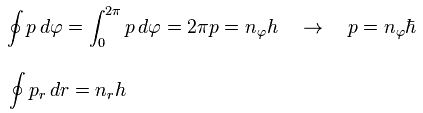
where the angular momentum p is constant.
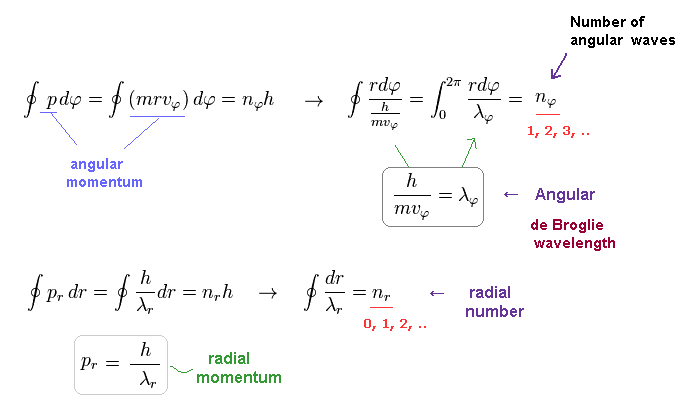
So p becomes an integer (= nφ ) times ħ
By the way, what do Eq.32 mean ?
If we use the de Broglie relation in each direction ( tangential and radial ),
(Eq.33)
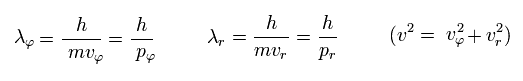
Eq.32 means
(Eq.34)
So they express quantization of de Broglie wavelength in each direction.
In Schrodinger equation, the unreal zero angular momentum (= angular nφ = 0, radial nr is not zero, which is the linear s-orbital ) is possible, while in the realistic Bohr-Sommerfeld atomic model, the angular quantum number (= nφ ) must be non-zero to prevent electrons from crashing into nuclei (= when the radial nr is zero, it's a circular orbit ).
The radial quantization condition can be rewritten as
(Eq.35)
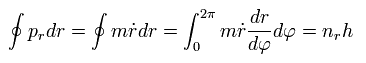
Using Eq.27,
(Eq.36)
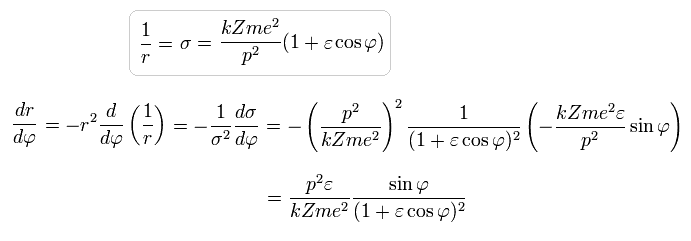
And from Eq.28,
(Eq.37)
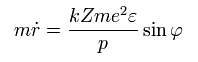
From Eq.35-37, we have
(Eq.38)
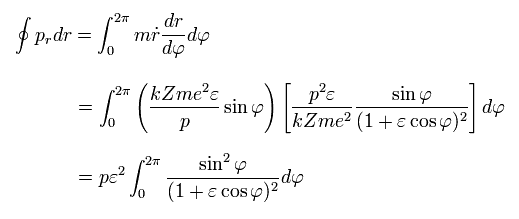
Doing the integration by parts in Eq.38,
(Eq.39)
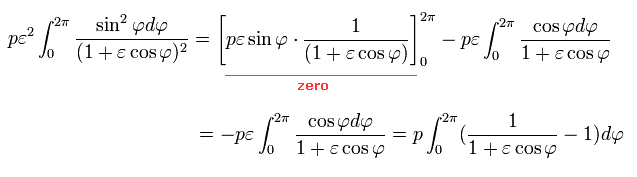
Here we use the following known formula (= complex integral, see this p.4-5, this p.2, this p.1-2, this p.24-25, this p.5 ),
(Eq.40)
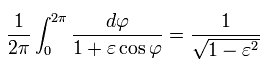
--------------------------------------------------------------
According to Euler's formula, cosine can be expressed using the complex number z,
(Eq.41)
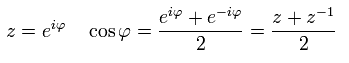
So,
(Eq.42)
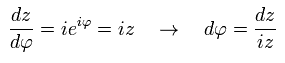
Using Eq.41 and Eq.42, the left side of Eq.40 is
(Eq.43)
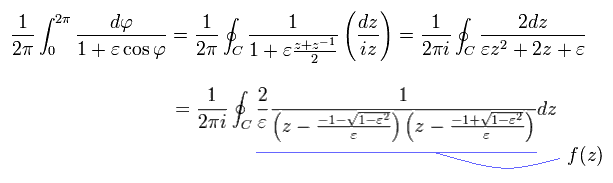
where
(Eq.44)
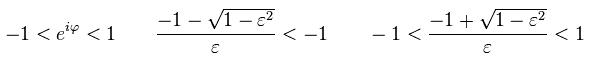
So only the latter number of Eq.44 is used as "pole" in Cauchy's residue theorem.
In the residue theorem, only the coefficient of 1/(z-a) is left, like
(Eq.45)
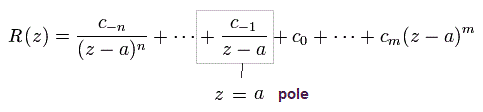 and
and
(Eq.46)
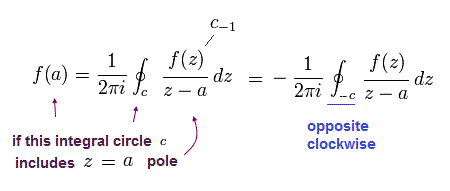
From Eq.43 to Eq.46, the result is
(Eq.47)
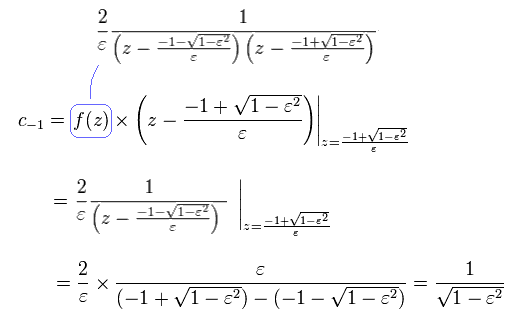
we can prove Eq.40.
---------------------------------------------------------------
Using the formula of Eq.40, Eq.38 (Eq.39) becomes
(Eq.48)
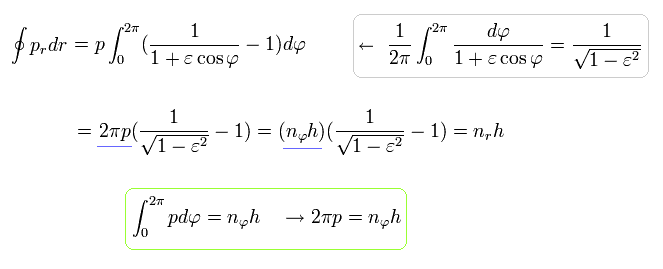
where the quantization of Eq.32 is used.
From Eq.48, we have
(Eq.48')
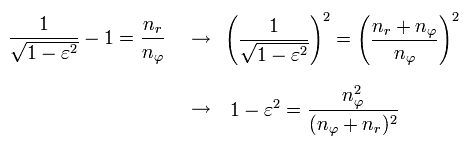
Substituting Eq.48' into Eq.31, and using Eq.32, the total energy W becomes
(Eq.49)
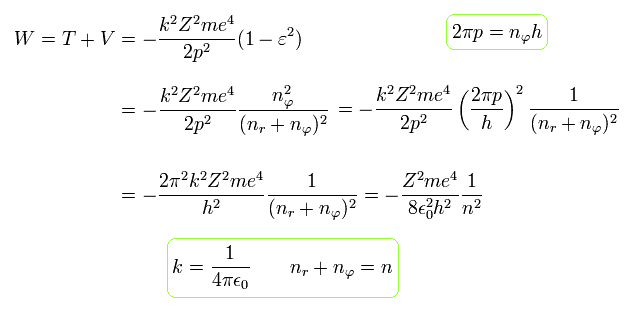
The above Eq.49 of the total energy levels (= W = T+V ) in Bohr-Sommerfeld hydrogen elliptical orbits is completely equal to the hydrogen energy E of both the quantum mechanical Schrodinger equation and Bohr's circular orbit ( this p.9, this p.17-(6.94), this p.15,35, this 4.10.5 ).
As a result, Bohr-Sommerfeld elliptical orbits proved to be a right atomic model which can perfectly explain atomic energy levels with various angular momentums.
Here we confirm Bohr-Sommerfeld solution of Eq.49 is valid also in the Schrodinger's hydrogen.
As shown on this page, the radial quantization number (= nr ) means the number of de Broglie waves included in the radial orbits.
And the nφ means quantized angular momentum (= de Broglie tangential wave's number).
(Eq.50)
Some orbitals of Schrodinger's wavefunction are
(Fig.27) Schorodinger's hydrogen = Bohr Sommerfeld model.
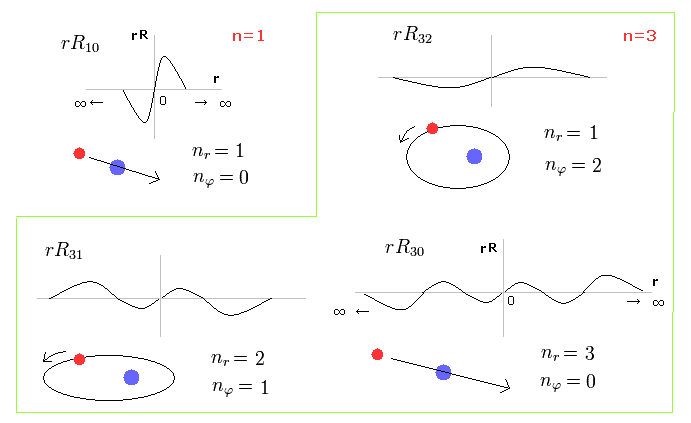
Fig.27 shows the energy levels of Schrodinger's wavefunctions just obey Bohr-Sommerfeld quantization rules.
The most important difference is that Schrodinger's solutions are always from zero to infinity, which is unreal.
(Fig.28) Why Schrodinger's hydrogen must NOT have circular orbits ?
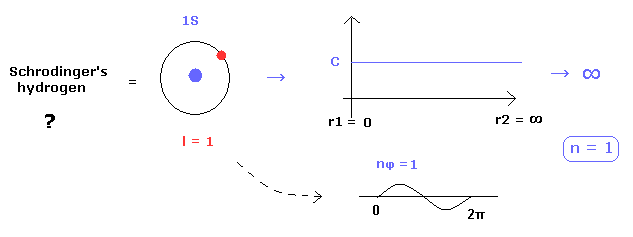
Schrodinger's hydrogen eigenfunctions consist of "radial" and angular momentum (= "tangential" ) parts.
As you know, Schrodinger's radial parts Always include "radial" momentum, which means there are NO circular orbitals in Schrodinger's hydrogen.
Because if the circular orbitals are included in Schrodinger's hydrogen, the radial eigenfunction needs to be constant (= C ), as shown in Fig.28.
So if this constant C is not zero, it diverges to infinity, when we normalize it.
( Schrodinger's radial region is from 0 to infinity. )
This is the main reason why Schrodinger's hydrogen includes many unrealistic "S" states which have no angular momentum.
(Fig.29) Angular momemtum L = 0 in S wavefunction → destructive interference of de Broglie wave !

As shown on this page, Schrodinger's wavefunctions also satisfy an integer number of de Broglie wavelength.
So in s orbital without angular momentum ( L = 0 ), opposite wave phases in one orbit cancel each other due to destructive interference in Schrodinger wavefunction.
As a result, stable wavefunction is impossible in "s" orbitals.
(Fig.30)
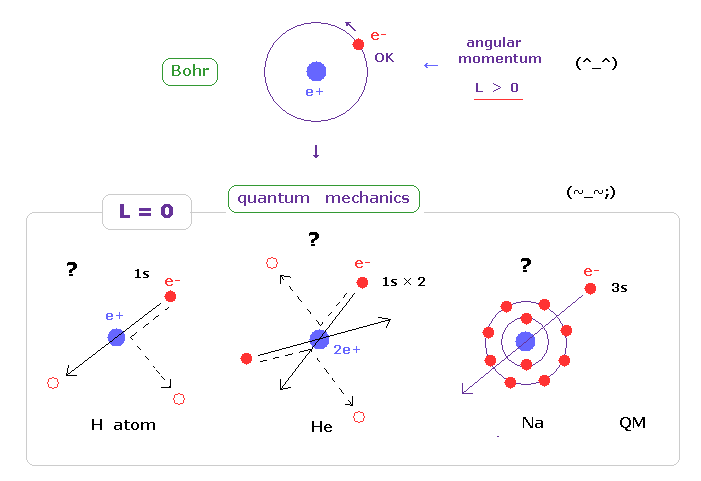
And electron in s orbital always crash ( or penetrate ) into nucleus ?
Also in multi electron atoms such as sodium and potassium, 3s or 4s electrons always penetrate the inner electrons and nucleus ?
As you feel, this unrealistic s state is impossible in this real world.
On this page, we have proved rigorously that Schrodinger's energies are equal to Bohr Sommerfeld's model.
(Ap.1) Bohr model hydrogen. -- Circular orbit.
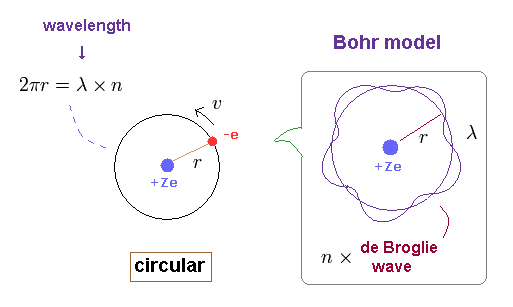
In this section, we review ordinary Bohr model ( see also this site (p.9) ).
First, as shown on this page, Bohr's single electron does NOT fall into nucleus just by acceleration.
Because vacuum electromagnetic energy around a single electron is NOT energy.
(Ap.2) Bohr model conditions.
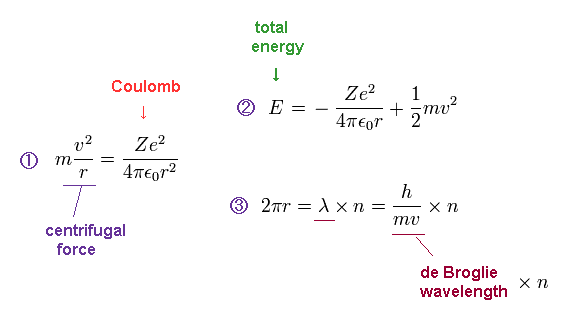
In Ap.2, the first equation means that the centrifugal force is equal to Coulomb force.
The second equation is the sum of Coulomb potential energy and kinetic energy.
The third equation means the circumference of one circular orbit is an integer (= n ) number of de Broglie wavelength.
Condition "1" is included in the condition "2". ( So two conditions "2" and "3" is needed for Bohr's orbit. )
Substituting equation "1" into equation "2",
(Ap.3)
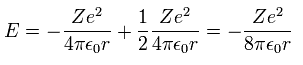
Inserting v of equation "3" into equation "1", we have
(Ap.4)
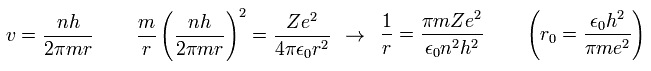
Here, "r0" ( n = Z = 1 ) means "Bohr radius".
"Bohr radius" and "Bohr magneton" are indispensable for quantum mechanics, which is the reason why Bohr model is taught in school even now.
Substituting Ap.4 into Ap.3, the total energy E of Bohr model is
(Ap.5) Bohr model = Schrodinger equation.
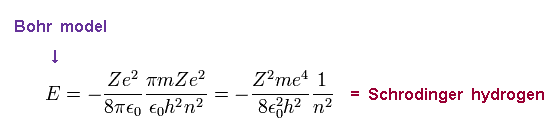
This energy E is the same as Schrodinger's hydrogen.
From Ap.4, the ratio of the particle's velocity v ( n=Z=1 ) to the light speed c is
(Ap.6) Fine structure constant α
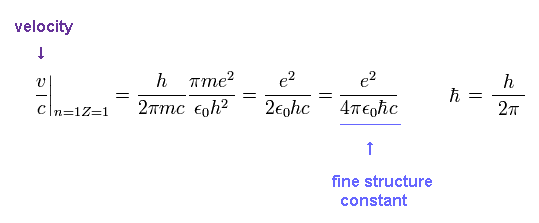
This is the famous fine structure constant α
So there is a strong tie between fine structure constant and Bohr's orbit.
(Ap.7) Radial (= pr ), tangential (= pφ )
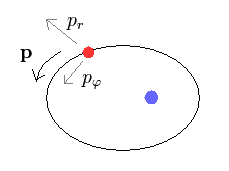
In elliptical orbit, we can divide momentum (= p ) into radial (= pr )
and angular (= pφ ) components.
According to the Pythagorean theorem, we have
(Ap.8)
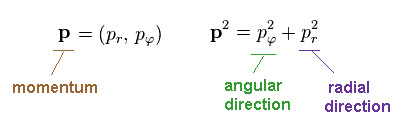
Dividing momentum (= p ) by mass (= m ), we get velocity "v".
We suppose the electron travels the distance "dq" during the infinitesimal time interval "dt".
(Ap.9)
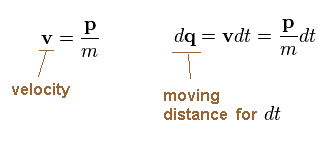
Using Phythagorean theorem, the moving distance "dq" can be separated into radial and angular (= tangential ) directions.
(Ap.10)
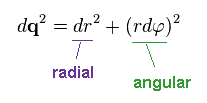
In Ap.10, "r" is the radius, and φ is the angle.
Like Ap.9, we have
(Ap.11)
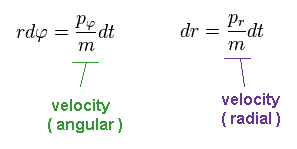
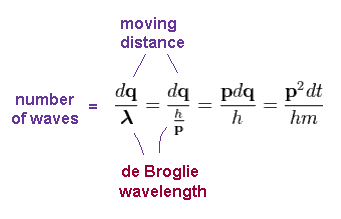
Using de Broglie wavelength (= λ = h/p ), number of de Broglie waves contained in small region "dq" becomes
( Using Ap.9 )
(Ap.12)
In the same way, using de Broglie wavelength in radial (= λr ) and tangential (= λφ ) directions, number of waves contained in each segment becomes ( using Ap.11 )
(Ap.13)
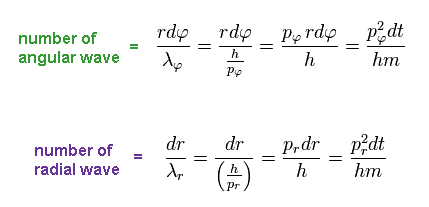
From Ap.12 and Ap.13, we get the relation of
(Ap.14)
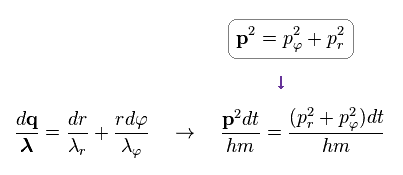
As a result, we have
(Ap.15) Total number of de Broglie waves n = nr + nφ
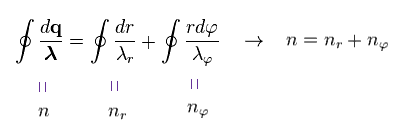
Doing the line integral along the orbit in both sides of Ap.14, we get the result of Ap.15.
"n" means the total numebr of de Broglie wavelength, and is equal to principal quantum number.
"nr" denotes the number of radial de Broglie wavelength along radial path.
"nφ" denotes the number of tangential de Broglie wavelength along tangential direction.
The relation of n = nr + nφ holds.
(Ap.16) Actual relation between angular and radial wavelengths.
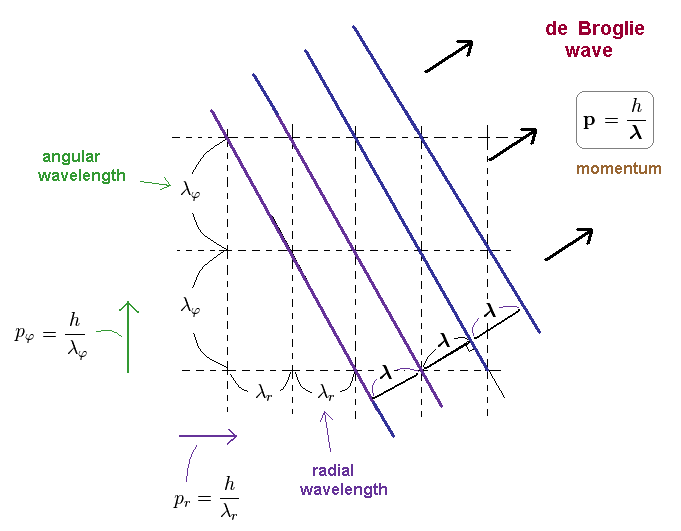
We can explain the reason why de Broglie waves can be separated into angular and radial directins.
The matter wave of Ap.16, has de Broglie wavelength of λ, so the total momnetum p = h/λ.
As you see Ap.16, angular and radial de Broglie wavelengths are longer than the total wavelength.
( λφ, λr > λ ).
(Ap.17) Angular and radial components of momentum "p"
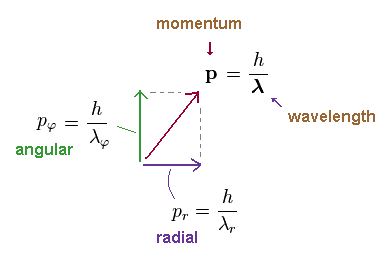
Angular (= pφ ) and radial (= pr ) components of the whole momentum "p" must satisfy Pythagorean theorem, as shown in Ap.17.
From Ap.16, you find λ can be expressed as
(Ap.18)
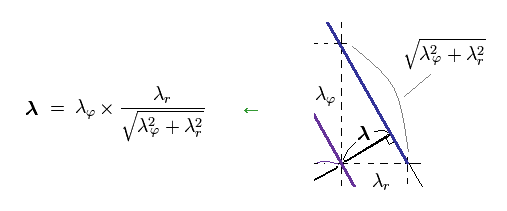
Substituting Ap.18 into the total momentum p of Ap.17, we find de Broglie relation satisfies Pythagorean theorem, as follows,
(Ap.19)
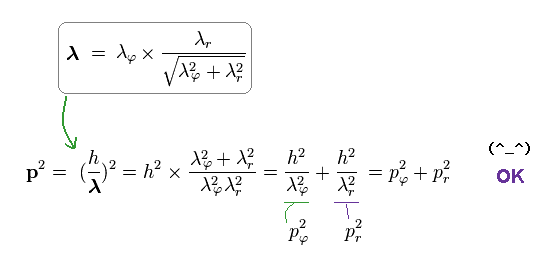
As a result, de Broglie relation of p = h/λ agrees with classical mechanics, too.
(Ap.20) Total, angular, radial directions = an integer × de Boglie wavelength.
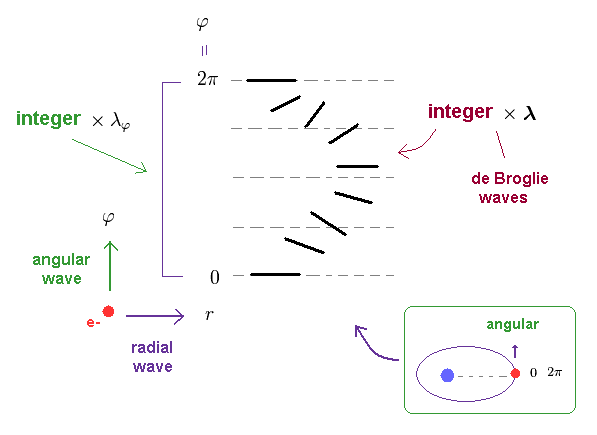
In hydrogen-like atom, the orbit becomes elliptical or circular.
So, at two points ( apherion and perihelion ), an electron moves in angular direction.
Of course, at the same point ( φ = 0 and 2π ), the wave phase must agree with each other.
As shown in Ap.20, when the circumference of the whole elliptical orbits is equal to an integer number of de Broglie wavelength, the path in the angular direction also satisfies an integer × ( tangential ) de Broglie wavelength.
As I said in Ap.15, the number of "radial" waves is given by nr = n - nφ.
So in this case, "radial" direction also satisfies an integer (= nr ) × de Broglie wavelength.
(Ap.21) Schrodinger equation of hydrogen.
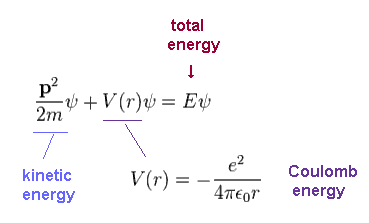
In this section, we solve the Schrodinger equation of hydrogen atom, like on this site and this site.
ψ is total wavefunction of hydrogen.
Total energy E is the sum of kinetic energy and Coulomb potential energy (= V ) both in Schrodinger and Bohr's hydrogens.
(Ap.22)
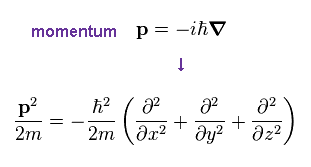
Schrodinger equation also uses de Broglie relation ( λ = h/p ), so momentum p is replaced by operater, as shown in Ap.22.
Using spherical coodinate,
(Ap.23)
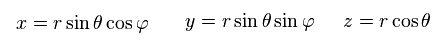
Ap.22 becomes
(Ap.24)
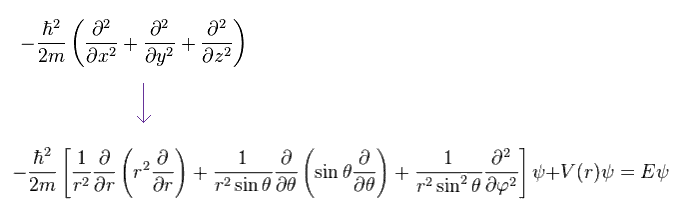
They use the form of wavefunction that assumes the separation into radial (= R ) and angular (= Y ) portions, as follows,
(Ap.25)
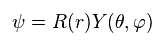
Dividing both sides of Ap.24 by
(Ap.26)
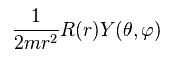
we have
(Ap.27)
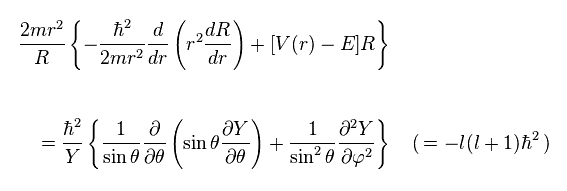
The left side of Ap.27 is dependent only on radial variable "r".
And the right side is angularly-dependent (= θ and φ ) equation.
So we can consider both sides as some constant (= -l(l+1)ħ2 )
As a result, the left side of Ap.27 becomes
(Ap.28)
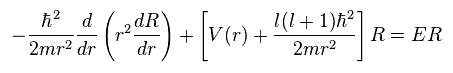
The right side of Ap.27 becomes
(Ap.29)
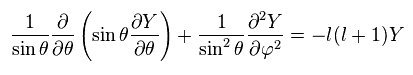
We replace Y by a product of single-variable functions. ( Y → θ and φ )
(Ap.30)
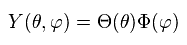
Inserting Ap.30 into Ap.29, and dividing it by Φ,
(Ap.31)
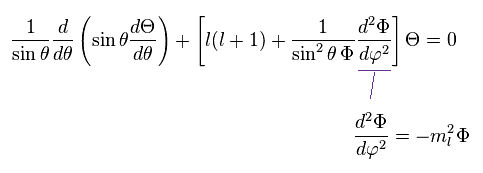
As a result, the azimuthal wavefunction Φ can be expressed as
(Ap.32)

ml must be an integer, otherwise the value of the azimuthal wave function would be different for φ = 0 and φ = 2π. , as shown in Ap.33.
So in this case, the equation of Ap.24 is broken.
(Ap.33)
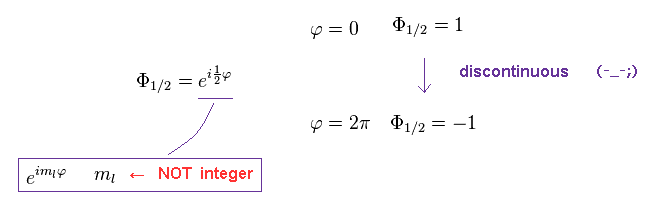
As shown in this section, Ap.32 means Schrodinger's hydrogen also obeys an integer number of de Broglie wavelength in angular direction. ← Sommerfeld quantisation.
(Ap.34)
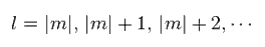
For angular equation of Ap.31 to have finite solution, angular constant l must satisfy Ap.34.
(Ap.28) Radial equation of hydrogen.
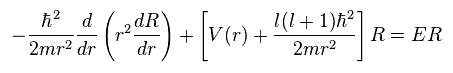
(Ap.35)
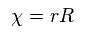
To make calculation easier, they substitute χ for rR in radial equation, as shown in Ap.35.
See also this site and this site.
Using this χ in Ap.28, we have
(Ap.36)
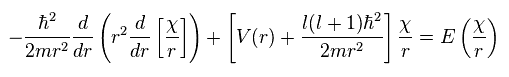
where
(Ap.37)
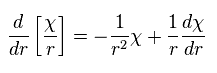
As a result, the radial part of Ap.28 becomes
(Ap.38)
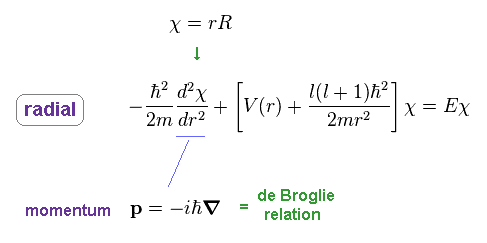
Ap.38 uses momentum operator based on de Broglie relation in radial direction.
So, this wavefunction χ shows de Broglie waves in radial direction.
Substituting ρ for βr,
(Ap.39)
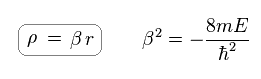
they express χ as
(Ap.40)
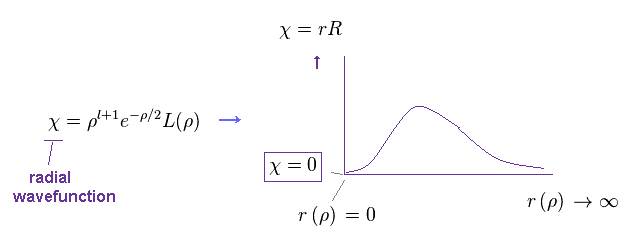
As you see the form of χ in Ap.40, this radial wavefunction always becomes zero at both ends ( χ = 0, r =0 and ∞ ).
So, at this point, this χ becomes an integer times de Broglie wavelength.
L(ρ) is a polynomial in ρ,
(Ap.41)
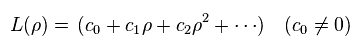
For this polynomial to have finite terms, the enrgy E must be quantized as follows,
(Ap.42)
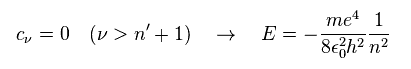
The principal quantum number n is the sum of angular and radial quantum numbers.
(Ap.43)
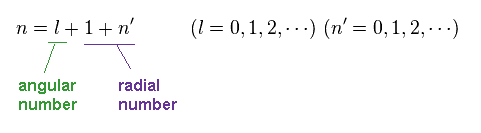
This energy solution just agrees with that of Bohr-Sommerfeld model.
In both of Schrodinger and Bohr's hydrogens, the sum of radial and angular ( wave ) numbers are important for energy levels (= n ).
(Ap.44) The same mechanism is used in Schrodinger and Bohr-Sommerfeld models.

2014/6/11 updated. Feel free to link to this site.