Top page ( quantum mechanics is wrong ) (← 6/15/2025 )
End of Schrodinger equation.
Truth of the fine structure constant α.
What does Planck constant really mean ?
True mechanism of useless quantum chemistry.
It is said that Schrodinger equation of quantum mechanics can give very exact energy values of various atoms.
But we cannot solve the equations other than simple hydrogen-like atoms.
So we need to use some approximation.
In these approimations, variational methods can give most exact values about the energies of atoms.
(Fig.1) Quantum mecanical helium becomes chaotic and unstable.

But as you know, the quantum mechanical atoms can NEVER tell us true states of electron's motion.
A single electron is actually quantized particle with definite mass and charge -e according to experiments.
So it is inconsistent with the experimental results to insist one electron is spreading into all space as clouds.
Furthermore, if two electrons of stable helium has NO angular momentum (= 1s ), this helium model would be extremely unstable.
It means that quantum mechanical peturbation or variational methods cannot express real states of atoms at all.
(Eq.1) Hamiltonian of helium atom.
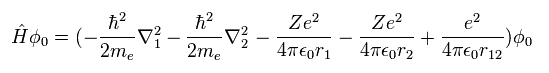
Helium-like atom has two nagative electrons ( 1 , 2 ), and one positive nucleus (= +Ze ).
( In neutral helium atom, this Z is "2". )
Two first terms of Hamiltonian in Eq.1 represent kinetic energies of electron 1 and 2.
And the last term of Eq.1 is repulsive Coulomb interaction between two electrons.
( r12 is the distance between two electrons. )
(Eq. 2) "1s" wavefunction of hydrogen-like atoms.
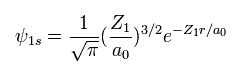
When we try to solve helium's Schrodinger equation, we use 1s wavefunction of hydrogen-like atom.
( Z1 = 1 is hydrogen atom, and Z1 = 2 is helium ion. )
Using two wavefunctions of Eq.2, we express neutral helium wavefunction, as follows,
(Eq. 3)
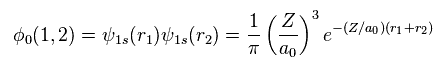
Substituting Eq.1 and Eq.3 into the energy (= W ) equation of
(Eq. 4)
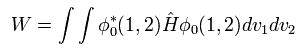
we obtain
(Eq. 5)
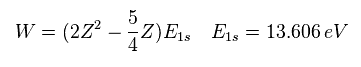
When Z = 2, the total energy W of helium becomes -74.833 eV, which is different from the experimental value of -79.0051 eV.
Changing the atomic number Z, we get ground state energies of various helium-like atoms (ions), as follows,
| Atoms | Experiment (eV) | new Bohr (eV) | Perturbation (eV) | Bohr Error | Pert Error |
|---|---|---|---|---|---|
| He | -79.0051 | -79.0037 | -74.8330 | +0.001 | +4.172 |
| Li+ | -198.093 | -198.984 | -193.885 | -0.89 | +4.21 |
| Be2+ | -371.615 | -373.470 | -367.362 | -1.85 | +4.25 |
| B3+ | -599.60 | -602.320 | -595.262 | -2.72 | +4.34 |
In Table 1, "perturbation" means quantum mechanical approximation and "new Bohr" means computed Bohr's orbits which are perpendicular to each other as shown in Top page or Fig.2.
(Fig.2) New Bohr model Helium.
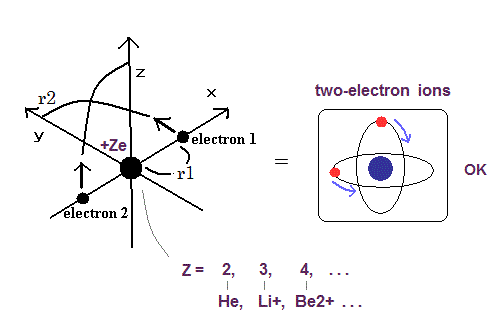
New Bohr's helium model can give just exact ground state energy ( except only for small relativistic effect ).
And of course, Bohr's orbits can also give concrete electron's motion, and agree with de Broglie wave's nature and stability of helium.
So we can apply this model to 1s inner states of various other atoms.
As you notice, quantum mechanical pertubation methods show almost same error (= about +4 eV ), even when the atomic number is bigger.
This is unnatural.
(Eq. 6) Variation functions.
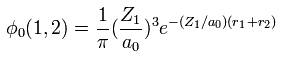
Next we try quantum mechanical variational methods of helium-like atoms.
Here we consider charge Z1 as variational parameter and change it.
Substituting Eq.6 into Eq.4,
(Eq. 4)
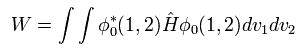
We obtain,
(Eq. 7)
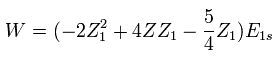
In Eq.7, "Z" is atomic number included in Hamiltonian of Eq.1.
So this Z is fixed value, which is different from variational parameter Z1.
We vary Z1 to minimize the total energy as follows,
(Eq. 8)
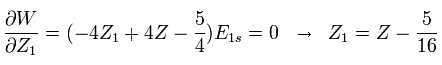
For example, in neutral helium ( Z = 2 ), when Z1 = Z -5/16 = 2-5/16 = +1.6875, the total energy becomes the lowest value.
Substituting this Z1 = Z - 5/16 into Eq.7, the total energy W becomes,
(Eq.9)
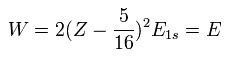
For example, substituting Z = 2 and E1s = -13.606 into Eq.9, the total energy (E) becomes -77.49 eV, which is closer to the experimental value (-79.005 eV) than the perturbation of Table 1.
But this is the limit of this method about two-electron atom.
| Atoms | Experiment (eV) | new Bohr (eV) | Variation (eV) | Bohr Error | Vari Error |
|---|---|---|---|---|---|
| He | -79.0051 | -79.0037 | -77.4904 | +0.001 | +1.515 |
| Li+ | -198.093 | -198.984 | -196.552 | -0.89 | +1.55 |
| Be2+ | -371.615 | -373.470 | -370.019 | -1.85 | +1.60 |
| B3+ | -599.60 | -602.320 | -597.919 | -2.72 | +1.68 |
As shown in Table 2, both new Bohr model and quantum mechanical variational method give good results.
But as you notice, variational methods cannot get the exact values especially in neutral helium and lithium ion.
And it is very unnatural that the error ( about +1.5 eV ) doesn't change much, even when the atomic number is bigger.
These results demonstrate that the quantum mechanical variational method does NOT express the true configuration of neutral helium.
( Of course, originally, quantum mechanical model has no reality. )
As the atomic number becomes bigger, true errors ( based on the repulsive interaction between two electrons ) are hidden under the influence by the big positive nucleus.
(Eq.10) Quantum mechanical helium.
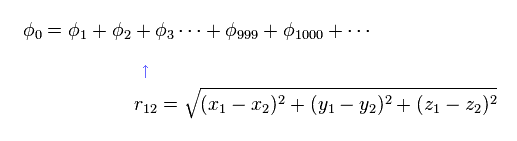
To get closer to the experimental values, we heve to use more than a thousand variational terms like Eq.10.
And to express repulsive force between electrons, these terms need to include variable ( r12 ), which is the distance between electrons.
So these wavefunctions can NOT show real helium state at all.
The existence of r12 means the probability at which we find electron 1 in some place is changing with respect to the position of electron 2.
So Eq.10 is NOT constant probability density wave.
(Eq.10') Electron clouds = signle electron is divided ?
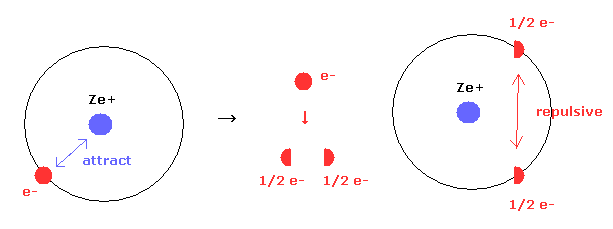
Quantum mechancs often insists that single electron of hydrogen ( or other atomes ) are spreading into all space as electron clouds.
But if a single electron is actually divided, these energy values are extremely higher due to new generated repulsive forces between fractional electrons.
In Eq.10' left, only attractive forces between nucleus and a single electron exists.
But if an single electron is divided into two fractional charges ( e- = -1/2 e -1/2 e ) as electron clouds, new repulsive forces are generated between them, though Coulomb attractive force remains the same.
This fact clearly indicates a single electron is not divided inside various atoms and molecules.
In this section, we explain why the above unrealistic variational methods can give values close to experimental values.
( See also true mechanism of useless quantum chemistry. )
(Eq. 11) "1s" hydrogen wavefunction.
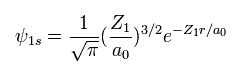
In the above section, we use 1s hydrogen-like wavefunction to get helium ground state energy.
As you know, Bohr model is completely equal to quantum mechnics in the energy levels of hydrogen-like atom.
So 1s wavefunction includes the same informations about average electron distribution (= Bohr radius ) and average kinetic energy (= T ).
(Fig.3) Bohr model = "1s" Wavefunction.
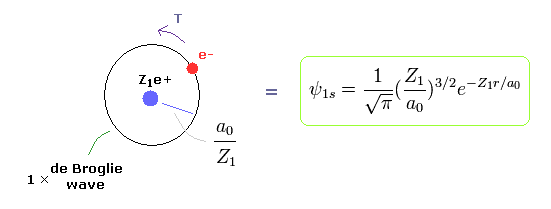
Quantum mechanical hydrogen also satisfies Virial theorem, E = 1/2V = -T .
( See Virial theorem of Schrodinger's hydrogen. )
So the same energy E means the same average kinetic energy T and distribution (= Bohr radius / Z1 ).
So from here, instead of 1s wavefunction, we use Bohr's orbit to explain variational methods.
When the electron is moving around the +Z nucleus on the orbit of radius r, the potential energy (V) is,
(Eq. 12)
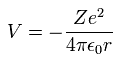
When Bohr's orbit is 1 × de Broglie wavelength, the average radius r becomes.
(Eq. 13)
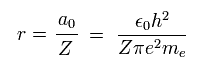
where a0 is Bohr radius.
As I said, Schrodinger's 1s wavefunction is also 1 × de Broglie wavelength around Ze+ nucleus.
See also this page. So the average potential energy (= distribution radius ) is the same as Bohr model.
According to Virial theorem, the total (E) and kinetic (T) energies at this average radius r become,
(Eq. 14)
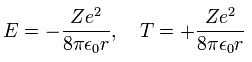
where E = 1/2 V, and T = -E.
When the variational charge parameter Z1 of Fig.3 changes ( nuclear charge Z doesn't change ),
the electron's distribution (= orbital radius ) changes, as follows.
(Eq. 15)
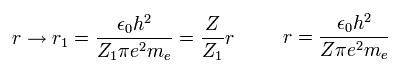
When the momentum operator acts on the wavefunction, it gives kinetic energy.
So the wavefunction itself includes the informations of kinetic energy (= momentum ).
As a result, the change of wavefunction causes the kinetic energy (T) change, as follows,
(Eq. 16)
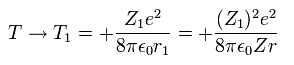
where Eq.14 and Eq.15 are used.
Only wavefunction's charge Z1 varies, and the nuclear charge (Z) keeps constant.
So the average potential energy (V) at r1 becomes,
(Eq. 17)
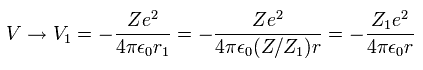
As a rsult, from Eq.16 and Eq.17, the total energy ( E = T + V ) becomes,
(Eq. 18)
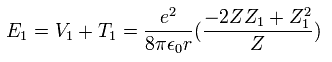
The partial differential of Eq.18 with respect to Z1 is
(Eq. 19)
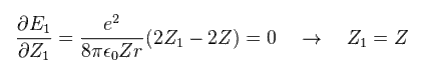
This result shows that when Z1 = Z, the total energy (E1) becomes the lowest
(Eq. 19') Mechanism of variational methods.
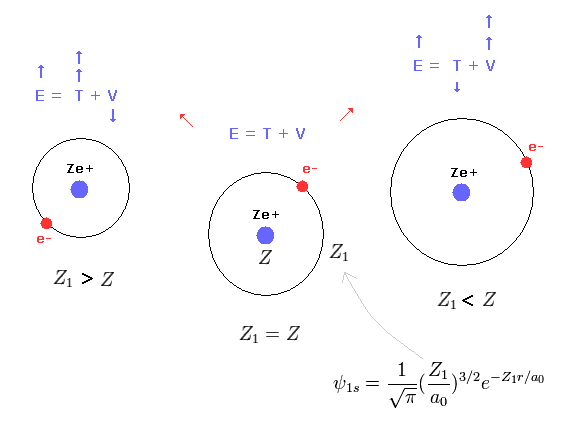
When Z1 becomes bigger than Z (= Eq.19' left ), the increase in kinetic energy (= T ) becomes bigger than the decrease in the potential energy (= V ). ( T is a square of Z1, compare Eq.16 and Eq.17. )
And when Z1 becomes smaller than Z (= Eq.19' right ), the decrease in kinetic energy is smaller than the increase in potential energy. ( So when Z1 =Z, total energy E is the lowest. )
This is the true mechanism of variational methods.
Here we use the atomic number Z.
But when the system includes several nuclei and electrons, average positive charges including overall particles mean this Z.
(Eq. 20) If we use 2s (or 2p) wavefunction ?
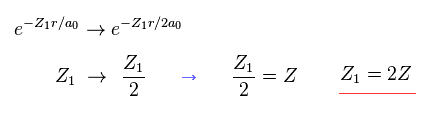
Even if we use 2s (or 2p ) type wavefunction, this result is the same as 1s function.
The difference is the value Z1 becomes twice the real atomic charge Z.
( In this case, 2s, 2p wavefunctions also mean 1 × de Broglie wavelength. )
(Eq.21) Hydrogen moelcule ion (H2+).
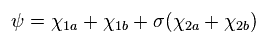
where
(Eq.22)
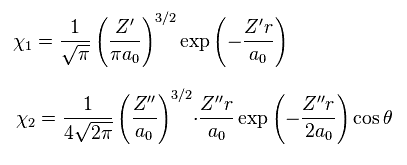
So as shown on this page, hydrogen molecule ion (H2+) variational functions give unrealistic Z values.
In Eq.21 χ1 is the 1s hydrogen atom wavefunction, and χ2 is 2p H atom wavefunction.
σ, Z' and Z'' are variational parameters.
Calculation results of variational methods are
(Eq.23)
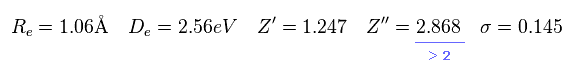
As you see in Eq.23, the positive charge of 2p wavefunction becomes 2.868.
Of course, H2+ molecule ion has only 2 nuclei, so Z'' = 2.868 is impossible.
They try to express 1 × de Broglie wavelenth using 2p wavefunction, so the variational charge Z'' becomes twice the real value. ( See Eq.20. )
(Fig.4) 2 × 1s wavefunction = helium.
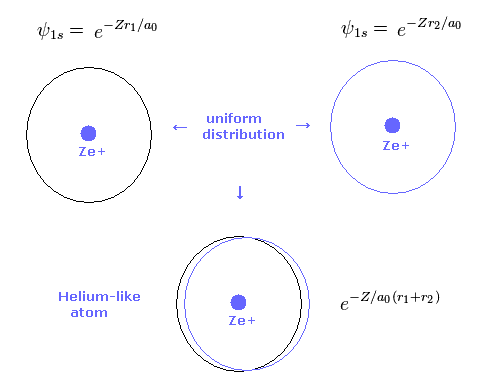
As shown in Table 2, the variational method can give similar results to new Bohr model.
Basically 1s hydrogen wavefunction is uniformly distributed around nucleus.
So also in variational helium model, two electrons are uniformly distributed around nucleus.
(Fig.5) New Bohr model = two electrons are uniformly distributed.
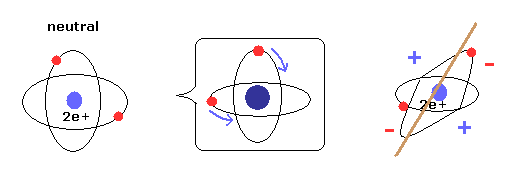
As shown on Top page, when two electrons' orbits are perpendicular to each other, it means two electrons are uniformly distributed around nucleus.
As a result, helium is not electrically poralized, and does NOT form compounds with other atoms or itself.
Due to the uniform distribution + variatinal charge Z (= average charge, see Eq.19 ), the variational method of Table 2 can give similar results to new Bohr model.
(Fig.6) Weak points of variational methods = NO clear motions.
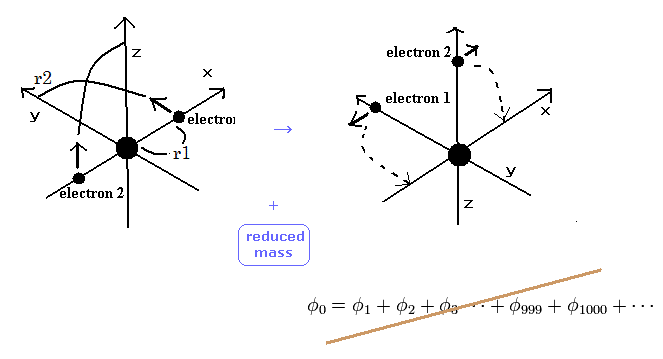
As shown in Table 2, variational method using 2 × 1s wavefunction can get -77.4904 eV, which is a little different from the experimental values of -79.0051 eV.
On the other hand, new Bohr model can get the exact value -79.0037 eV, except for small relativistic effect.
The difference between -77.4904 eV and -79.0051 eV is very important.
Because this difference is clearly caused by the replusive interaction ( motion ) between two electons.
Schrodinger's wavefunction can not show clear electron's motion and relative positions of two electrons, so it cannot explain the exact effects caused by the repulsive interactions and reduced mass.
This is the limit of variational methods.
In the upper section, we have proved that the variational methods of helium is similar to new Bohr model helium.
How about the lithium atom ?
The ground state energy of the lithium atom is -203.48 eV.
The hamiltonian operator of the lithium is,
(Eq.24)
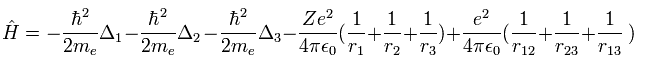
where Δ = ∇2.
If we calculate the lithium energy like Eq.4 and Eq.6, the result becomes -214.3 eV, which is lower than the experimental value.
This is strange.
This strange result is caused by the fact that the third electron of the lithium can not enter the 1S orbit.
So we need to restrict the variational wavefunction to get the correct result.
In the variational methods of the lithium, we use the following third-order determinant as the variational wavefunction.
(Eq. 25)
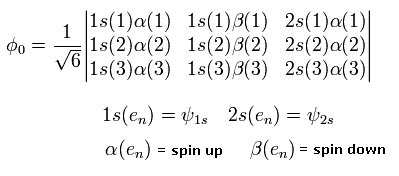
where 1S() and 2S() are the hydrogen wavefunctions.
And the numbers of 1,2, and 3 mean the electron numbers.
Why do we use the determinant ?
In the determinant, when the two electrons of them are in the same state, the whole wavefunction becomes zero.
If the wavefunction becomes zero, the total energy becomes zero, which is higher than the ground state energy ( -203.48 eV ).
So we can't use the 1S wavefunction in the third electron of the lithium.
When we use Eq.25, and vary the variational parameters Z1 and Z2, the minimum total energy of the lithium becomes -201.2 eV, which is close to the experimental value ( -203.48 eV ).
In this case, Z1 and Z2 are +2.686 and +1.776, respectively.
Because the two 1S electrons are closer to the nucleus than the 2S electron.
Surprisingly, these approximate value close to the experimental one was gotten in 1933 by manual calculation of the variational methods.
(E.B. Wilson, Jr., J. Chem. Phys., 1, 210, 1933)
But of course, "real" Bohr model could not give this excellent value in 1933 due to the lack of computers.
| Atoms | r1 (MM) | WN x 4 | Result (eV) | Experiment | Error (eV) |
|---|---|---|---|---|---|
| Li | 1949.0 | 1.000000 | -203.033 | -203.480 | 0.47 |
| Be+ | 1427.0 | 1.000000 | -388.785 | -389.826 | 1.04 |
| B2+ | 1125.0 | 1.000000 | -635.965 | -637.531 | 1.56 |
| C3+ | 928.0 | 1.000000 | -944.46 | -946.57 | 2.11 |
| N4+ | 790.5 | 1.000000 | -1314.25 | -1317.01 | 2.76 |
| O5+ | 688.0 | 1.000000 | -1745.70 | -1748.82 | 3.12 |
| F6+ | 609.4 | 1.000000 | -2237.60 | -2242.21 | 4.61 |
| Ne7+ | 546.0 | 1.000000 | -2791.15 | -2797.12 | 5.97 |
(Fig.7) Three electron atomic model.
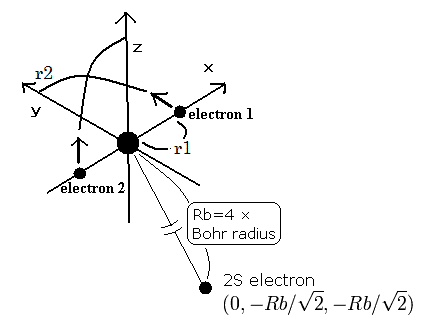
As shown in Table 3 or this page , our new Bohr model lithium (= Fig.7) gives -203.033eV, which is more correct.
And other three-electron atoms (ions) can be explained using new Bohr's model correctly, too.
When the Z1 is bigger, and Z2 is smaller, the distributions of the 1S and 2S electrons are more apart from each other. (Fig.8)
(Fig.8) The change of the probability density in 1S and 2S electrons.
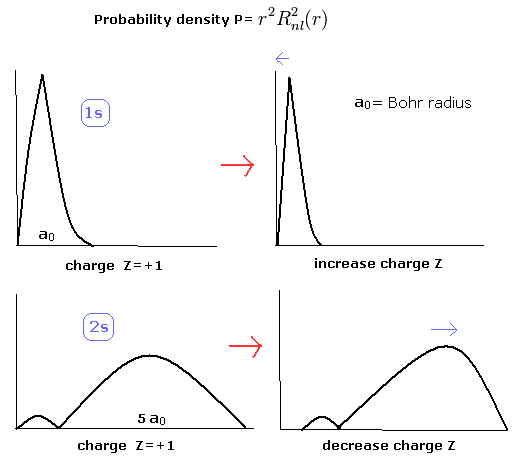
So in the lithium, the overlapping parts of the 1S and 2S wavefunctions become small, and the loss by the antisymmetric property of the determinat becomes small, too.
Of course, the distributions of the 1S (Eq.2) and 2S electrons (of hydrogen-like atoms) are the same as the Bohr model (= the potential energies are the same in Bohr model and the quantum mechanics.)
So also in the lithium, Bohr model is similar to the quantum mechanics.
But as shown on this page, mathematical ( not physical ) concepts such as wavefunctions and determimants clearly obstructs the development of science.
(Fig.9) Superposition = unrealistic Many-worlds !
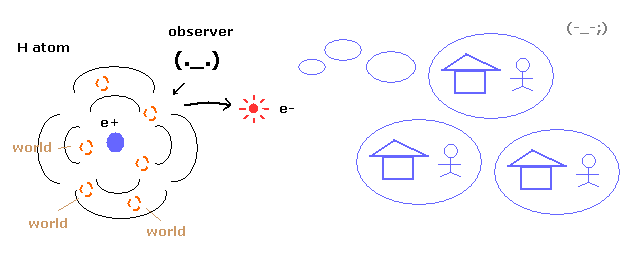
As you know, quantum mechanics cannot describe the electron's concrete motion at all.
It only shows the probability density of the electron in hydrogen atom.
So to explain wavefunction collapse, we need unrealistic many worlds.
(Fig.10) 1 × de Broglie wavelength = hydrogen ground state.
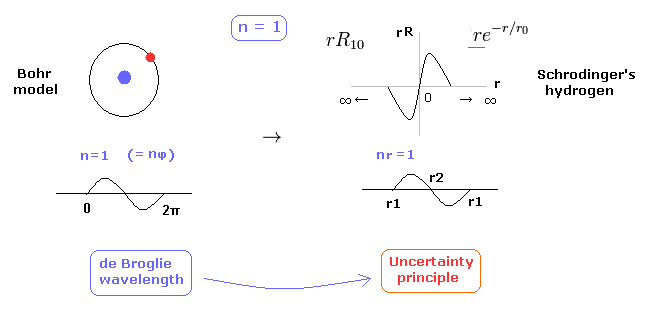
As shown on this page, Schrodinger's hydrogen also satisfies the condition of an integer times de Broglie wavelength.
This is the reason why Schrodinger's hydrogen gives completely the same results as Bohr model.
As shown in Fig.10, in the ground state of hydrogen atom, Bohr model consists of tangential de Broglie wave, and Schrodinger's model ( rR ) consists of "radial" de Broglie wave.
( It is easily understood also by seeing the probability graphs of |rR|2. )
Actually, the probability of ground state of hydrogen is the highest around Bohr radius.
The problem is that Schrodinger's radial wavefunction must be always from zero to infinity.
And the 1s de Broglie wave is linear, so the opposite phases of them overlap and cancel each other out.
(Fig.11) Schrodinger's wavefunctions always spread to infinity.
In various atoms and molecules such as helium and hydrogen molecule, Schrodinger's wavefunction ALWAYS spread to infinity.
This means we can find the bound-state electron near infinity even in very stable helium atom !
Of course, this is impossible, and quantum mechanics ( chemistry ) has NO ability to describe real states of various atoms and molecules.
Schrodinger's equation of helium atom cannot be solved, but variational functions of it are always spreading to infinity.
(Fig.12) Schrodinger's 2P "radial" wave function (angular momentum = 1).
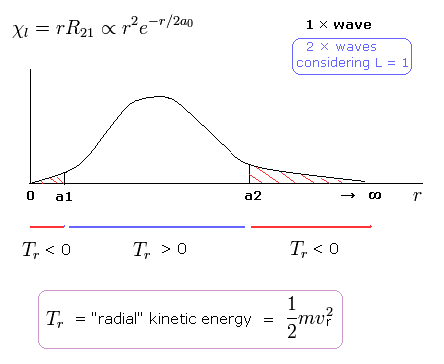
As shown in Fig.12, the 2P "radial" wave function ( χ = rR21 ) contains the regions of the minus kinetic energy ( r < a1, a2 < r ).
When the r is bigger than a2, the Coulomb potential energy becomes higher than some maximum value.
In this region, to keep the total energy (E < 0) constant, the "radial" kinetic energy must be minus !
Furthermore, in the region from 0 to a1 of Fig,12, the potential energy is lower than the total energy.
But the tangential kinetic energy increases much faster than others.
To cancel the increased tangential kinetic energy, radial kinetic energy has to be minus.
These unreasonable states clearly show Schrodinger's hydrogen atom is wrong.
(Fig.13) Quantum mecanical helium becomes chaotic and unstable.

In the quantum chemistry, if we use two 1s wavefunction of hydrogen atom, we can get the approximate gound state energy of helium.
But as you notice, 1s state has NO angular momentum.
In this state, two electrons of helium become chaotic and very unstable due to repulsive Coulomb force between them.
So the quantum mechanical helium is completely different from the actual helium atom.
(Fig.14) Quantum mechanical helium.
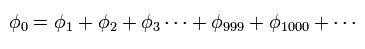
To get the exact ground state energy of helium (or hydrogen molecule ) using Schrodinger's equation, we have to use more than a thousand variational functions, as shown in Fig.14.
(Fig.15) Probability density of helium or H2 ?
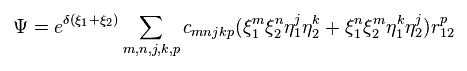
And these variational functions must include the variables (= r12 ) which express the distance between two electrons.
So, different from static hydrogen atom, the probability density at which we find electron 1 of helium (or H2 ) is always changing depending on the position of electron 2.
This variational functions of helium clearly shows the two electrons of helium are actually moving, even in the vague probability density.
(Fig.16) Reduced mass = electrons and nucleus are actually moving !
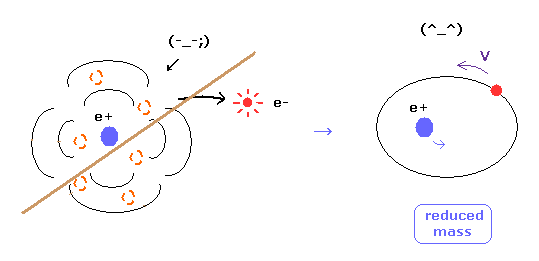
As you know, if we use the reduced mass of electron, we can get more exact values of the energy levels even in hydrogen atom.
This fact clearly shows that the electron and nucleus are actually moving interacting with each other.
Of course, as fractional charges of electron have not been found, we have to express real motions of the two electrons in helium atom.
As shown on this page, even pilot wave (Bohm) theory cannot explain two-electron helium at all, in quantum mechanics.
(Fig.17) Calculation results using reduced mass are more exact.
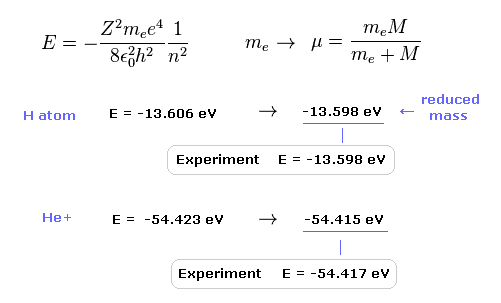
The experimental value of ground state hydrogen is -13.598 eV.
When we calculate this ground state energy using Schrodinger equation (or Bohr model ), it becomes -13.606 eV.
If we replace the usual electron mass by reduced mass considering nuclear motion, this calculation result becomes more exact (= -13.598 eV ).
This fact clearly shows the bound-state electron (and nucleus ) is actually moving.
Also in helium ion ( He+ ), if we use reduced mass, we can get more exact result (= -54.415 eV ) than the usual electron mass (= -54.423 eV ).
The experimental value of He+ is -54.417 eV.
(Fig.18) Two-electron Atomic Model ( He, Li+, Be2+, B3+, C4+ ... )

As shown on Top page, if the two de Broglie waves (= 1 × wavelength ) are overlapping each other, their opposite wave phases cancel each other due to destructive interference.
( These destructive interferences of electron's de Broglie waves were actually observed in Davisson and Germer experiments. )
So the two electrons's orbit have to be perpendicular to each other to avoid destructive inteference.
| Atoms | r1 (MM) | WN x 4 | Circular orbit | Result (eV) | Experiment | Error (eV) |
|---|---|---|---|---|---|---|
| He | 3074.0 | 1.000000 | -83.335 | -79.0037 | -79.0051 | 0.001 |
| Li+ | 1944.5 | 1.000000 | -205.78 | -198.984 | -198.093 | -0.89 |
| Be2+ | 1422.0 | 1.000000 | -382.66 | -373.470 | -371.615 | -1.85 |
| B3+ | 1121.0 | 1.000000 | -613.96 | -602.32 | -599.60 | -2.72 |
| C4+ | 925.0 | 1.000000 | -899.67 | -885.6 | -882.1 | -3.50 |
| N5+ | 788.0 | 1.000000 | -1239.8 | -1223.3 | -1219.1 | -4.20 |
| O6+ | 685.3 | 1.000000 | -1634.38 | -1615.44 | -1610.70 | -4.74 |
| F7+ | 607.3 | 1.000000 | -2083.3 | -2062.0 | -2057.0 | -5.00 |
| Ne8+ | 544.5 | 1.000000 | -2586.7 | -2563.0 | -2558.0 | -5.00 |
As shown in Table.4, these two-electron atomic model can completely explain actual energy states of various atoms.
The helium ground state energy ( -79.0037 eV ) is more exact than the latest quantum mechanical variational methods ( -79.015 eV ), because quantum mechanical helium cannot deal with nuclear motion ( reduced mass ) correctly.
About the computing methods and programs, see this page.
And this model can express three-electron atoms such as lithium correctly, too.
(Fig.19) New Bohr's helium (= A.) is not electrically polarized.
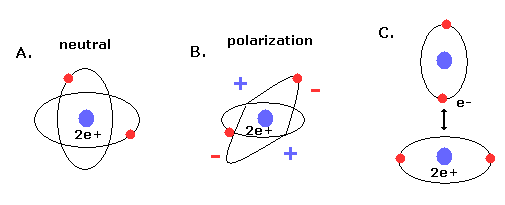
Furthermore, this helium model is just consistent with the fact that helium atom is most stable and doesn't form compounds with other atoms (or itself ).
Because when the two orbits are perpendicular to each other, the space around 2e+ nucleus becomes just neutral due to uniform distribution.
And of course, there is no space into which the third electron enter in Fig.18 helium, considering the stability of de Broglie waves (= Pauli exclusion principle ).
If the third electron enter them, destructive interferences of their de Broglie waves make them unstable.
(Fig.20) "Mathematical" Schrodinger equation vs. "real" Bohr model.
We cannot know what the Schrodinger's wavefunctions really are and just give up asking what they are.
Furthermore, as shown on this page, even if we study about relativistic quantum field theory and string theory, we cannot know what mysterious Pauli exclusion principle really is.
They just insist anticommutation of mathematical operators means Pauli exclusion principle.
So, as shown on this page, we cannot develop and try easier and useful methods in this very limited and vague conditions.
As this useless present quantum chemistry cannot be applied to various fields such as molecular biology and nanotechnology, their developments all stop now in the molecular levels. This is serious problem.
(Fig.21) Density functional theory = approximation.
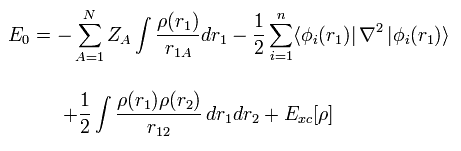
First, density functional theory (= DFT ), which is often used now, is only approximation, and NOT ab-initio method.
DFT is one of semi-empirical methods.
We can artificially choose various approximations such as LDA to match experimental results.
So popular DFT itself is NOT a true theory.

2013/2/9 updated. Feel free to link to this site.