Relativistic quantum field theory, Dirac equation, photons are useless, unphysical.

Home page
QED is wrong.
Dirac hydrogen atom
Particle physics is unreal

Relativistic quantum field theory, quantum electrodynamics (= QED ) is useless, just describing electrons and fictitious photons as unphysical math symbols lacking real particle shape.

(Fig.1)  Relativistic quantum field theory = Dirac equation is unreal.

Relativistic quantum field theory lacks reality.

Relativistic quantum field theory, QED, particle physics is just an unphysical useless theory unable to describe real particles.

Relativistic quantum field theory (= QFT ), quantum electrodynamics (= QED ) and today's useless particle physics, all of which are based on the unphysical Dirac equation ( this-p.9,  this-p.10-2.4 ), were artificially created by combining the unphysical quantum mechanics and paradoxical Einstein special relativity ( this-p.3 ).

Quantum field theory (= Dirac equation ) treats only unphysical particles lacking shapes.

The point is these quantum field theory, QED, particle physics are useless, unphysical, unable to express electrons and light (= or fictional photons ) as real particles except as the unphysical useless math operators ( this-p.7-10,  this-p.3- ).

All particles such as electrons, fictitious photons, antiparticles, quarks lack physical shape in unreal quantum field theory.

Quantum field theory and QED consisting of Dirac equation and wrongly-modified Maxwell equation can only describe each electron, (illusory) antiparticle and photon as an unphysical abstract math symbols (= with No real particle shape ) and matrices without real particle shapes ( this-p.9-10,   this-p.36,  this-p.17 ).

This unphysical Dirac equation is today's particle physics mainstream equation used to express all electrons, (illusory) antiparticles, quarks, neutrino called fermions, all of which are just nonphysical math symbols with No real particle shapes ( this-p.3-14,  this-p.1-8 ).

Einstein relativistic energy-momentum relation → unphysical Dirac equation treating γ matrices as (fake) spin. = quantum field theory

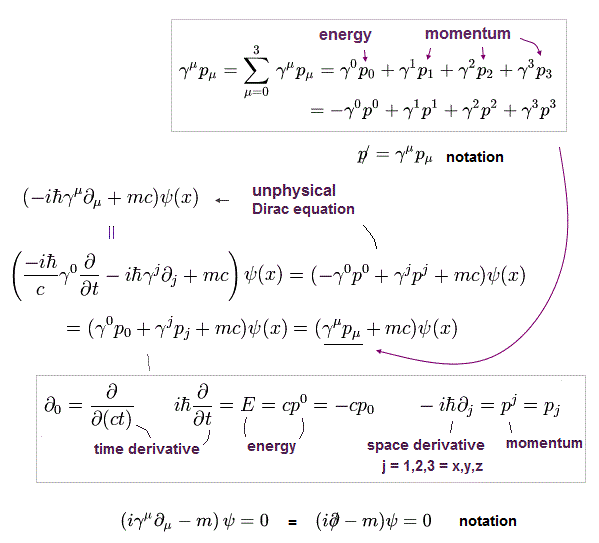
(Fig.2)  Paradoxical Einstein relativistic energy (= E ), momentum (= p ), mass (= m ) equation is divided into relativistic Dirac equation consisting of unphysical γ matrices.

Relativistic quantum field theory lacks reality.

Relativistic quantum field theory based on Dirac equation needs unphysical γ matrices to match paradoxical Einstein relativity.

Einstein's paradoxical relativistic energy (= E = p⁰/c ), momentum (= p1 = px, p2 = py, p3 = pz ), mass relation is an inconvenient quadratic equation.

To combine this (paradoxical) Einstein energy equation with quantum mechanics, physicists need to express the relativistic energy E as the time derivative, and the momentum p as the space derivative operators.

Klein-Gordon equation = original Einstein quadric energy equation

Klein-Gordon equation is the direct expression of this Einstein relativistic energy equation by using the quantum mechanical differential operators.

Dirac equation was obtained by falsely dividing Einstein quadric equation into linear equations with the help of unphysical γ matrices.

The current mainstream Dirac equation was obtained by dividing the quadratic relativistic energy (= Klein-Gordon ) equation into two linear equations by using the unphysical 4×4 gamma matrices ( this-p.22-26,  this-p.29-30,  this-p.2-5 ).

↑ These unphysical γ matrices including Pauli spin matrices are said to represent spin ( this-p.6-11,  this-p.5-6 ), which abstract math lacking real particle picture is irrelevant to the real phenomena, though.

Relativistic quantum field theory or Dirac equation's electrons and antiparticles are just unphysical math symbols irrelevant to real world phenomena.

(Fig.4)  Artificially-created Lagrangian (= L ) of Dirac equation.

Quantum field theory = Dirac equation is unreal.

Electrons and antiparticles of relativistic quantum field theory, Dirac equation are just unphysical math symbols with No shape.

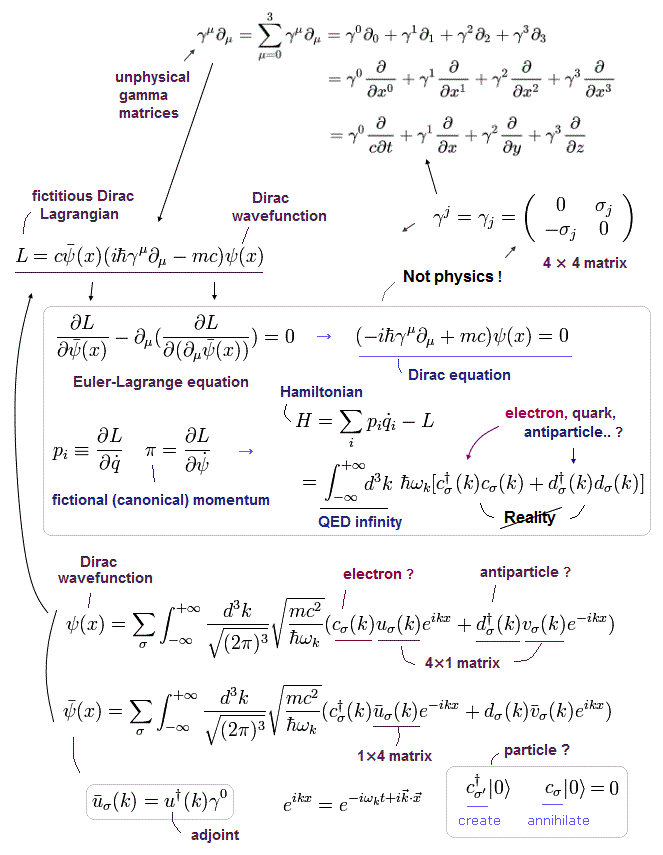
Relativistic quantum field theory based on Dirac equation is obtained by dividing the simple Einstein energy-momentum equation into linear equations with the help of unphysical γ matrices.

This relativistic Dirac equation expresses particles such as electrons, antiparticles, quarks.. only as unphysical math symbols (= a^†, b^† c^† d^†.. ) with No shape ( this-p.19,  this-p.24-p.30,  this-p.14-p.15 ).

And these (anti-)particle math operators are attached to the unphysical 4 × 1 spinor matrix such as u and v treated as artificial spin ( this-p.22-p.37,  this-p.13 ).

↑ All these definitions of unreal particles in relativistic Dirac equation are artificial, irrelevant to the real world.

Artificially-created Lagrangian (= L ) → modified Euler-Lagrange equation → unphysical Dirac equation.  ← Not prediction.

(Fig.5)  Lagrangian (= L ), which was artificially created, irrelevant to quantum field theoretical prediction  → Euler-Lagrange equation  → unphysical Dirac equation ?

Lagrangian is a meaningless math concept.

Lagrangian (= L ) for artificially deriving Dirac equation is just an unphysical concept irrelevant to the real world phenomena.

Quantum field theory tries to imitate classical mechanical (unphysical) Lagrangian (= L ) to artificially obtain relativistic Dirac equation and Hamiltonian through (modified) Euler-Lagrange equation.

Fig.5 shows the artificially-created Lagrangian (= L ) of the unphysical relativistic Dirac equation lacking real electron picture.

Relativistic quantum field theory, QED, particle physics rely on these artificially-created concepts called Lagrangian L (= "artificially-created" means No power to predict anything ) to justify their derivation of Hamiltonian (= H, total energy ) and (Dirac) energy-equation, though Lagrangian (= action ) itself has No physical meaning ( this-p.1-last ).

This website uses (-1. +1, +1, +1) relativistic metric notation.

Inseting the artificially-created Lagrangian into Euler-Lagrange equation gets Dirac equation ?

Physicists claim substituting the artificially-created Dirac' Lagrangian equation (= L ) into (artificial) Euler-Lagrange equation ( this-p.12 ) leads to the unphysical Dirac equation.

↑ The point is all these (Lagrangian) equations were artificially created (= Not derived from quantum mechanical theory ), irrelevant to prediction of relativistic quantum field theory or quantum mechanics.

Relativistic Dirac equation's Hamiltonian (= total energy ) is artificial, irrelevant to the real world.

(Fig.6)  Artificially-created Dirac Lagrangian (= L ) → Legendre transformation → Dirac's Hamiltonian (= total energy ), which is a useless equation.

Dirac's Hamiltonian (= total energy ) lacks reality.

Quantum field theory imitates classical Hamiltonian (= total energy ) obtained from artificially-created Lagrangian through Legendre transformation.

Quantum field theory tries to imitate classical mechanical Hamiltonian (= total energy ) obtained from the artificial Lagrangian through Legendre transformation ( this-p.9-p.10 ).

From the artificially-created Dirac's Lagrangian (= L ) irrelevant to relativistic quantum field theoretical prediction, they obtained Dirac equation's Hamiltonian H (= total energy ? ) via Legendre transformation using this, this (= adjoint Dirac spinor ) and γ matrix ( this-p.17,  this-5.466 ).

Relativistic quantum field theory or Dirac equation is useless, unphysical, unable to derive real Pauli principle, contrary to textbooks.

(Fig.7)  Artificially-created Dirac equation's Hamiltonian cannot describe Pauli principle, which is just unphysical math relation called anticommutation.

Unreal Pauli principle in Dirac equation.

Relativistic quantum field theory or Dirac equation cannot clarify real mechanism of Pauli principle nor antiparticles.

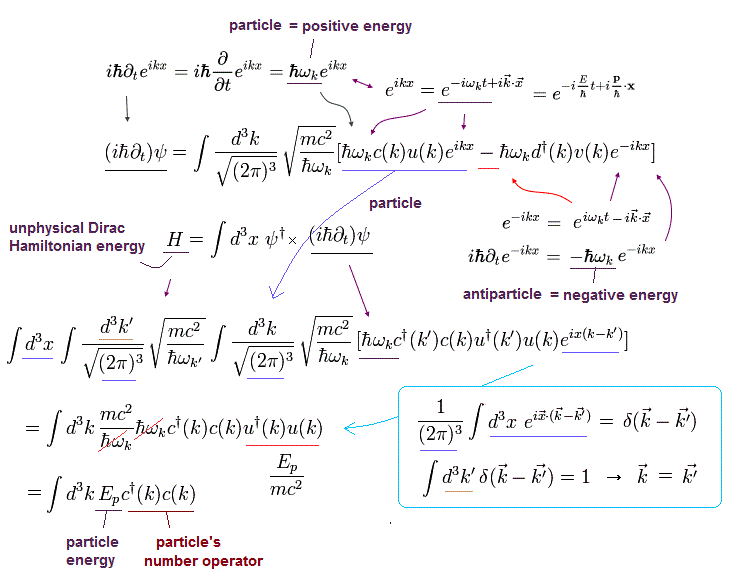
From the artificially-created Dirac equation's Hamiltonian (= total energy ) equation and unphysical math operators (= on this page, c, c^† represent electrons,  d, d^† represent antiparticles ), Pauli principle is said to be obtained ( this-p.3-6,  this-p.1-8 ).

As shown in Fig.7-lower, to obtain the antiparticle's energy E d^†d (= instead of dd^†, which meaningless order of unphysical particle operators is very important for Dirac equation ), the anticommutation relation (= d d^† = -d^†d ) is necessary ( this-lower,  this-p.2-5 ).

Dirac equation shows abstract anticommutation of unphysical math operators (= c^†, d^†.. = particles ? ) as fictitious Pauli principle.

Relativistic quantum field theory illogically claims this abstract meaningless anticommutation relation expresses Pauli principle, just because exchanging (anti)particles' (unphysical) math operators (= c, c^†, d, d^† ) changes the sign ( this-p.4  this-p.7,  this-p.2-3 ).

↑ unphysical anticommutation = d d^† = -d^†d  → if d = d^† (= if two particles occupy the same space ? ),  → d d = -d d  → d = 0 (= Pauli principle ?  this-p.56,  this-p.2-upper,  this-p.1-2 )  ← nonsense.

As I said, all these equation (= Hamiltonian, Lagrangian ) are just artificially-created, irrelevant to prediction of relativistic quantum field theory or QED based on Dirac equation which is just an unphysical math unable to explain the real world's phenomena.

Relativistic quantum electrodynamics (= QED ) shows just nonphysical math symbols lacking shape as (fictitious) photons.

(Fig.8)  Photons of relativistic quantum electrodynamics (= QED ) are just unphysical math symbols lacking real particle picture.

Photon doesn't exist.

Photons are just unreal math operators with No particle shape in relativistic Maxwell equation of quantum field theory.

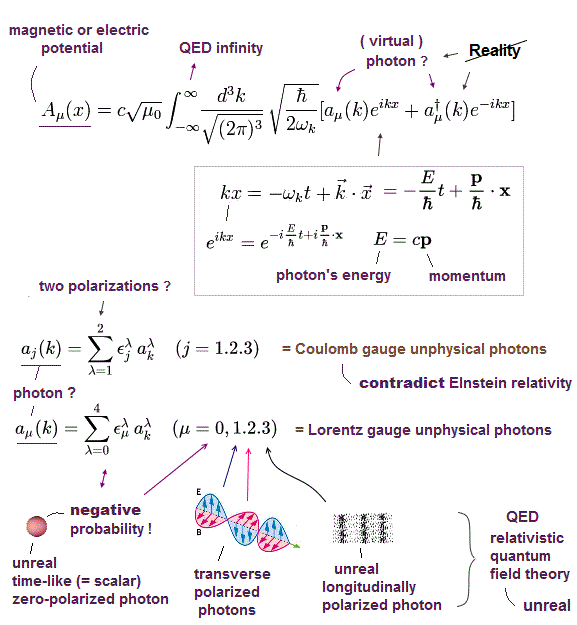
According to Maxwell equation incompatible with Einstein relativity, electric (= E ) and magnetic (= B ) fields can be expressed by electric or magnetic vector potential (= A  this-p.1-2 ).

Relativistic quantum field theory or QED tries to express an illusory photon as the unphysical math symbol (= a, a^† ) lacking real particle picture inside this electromagnetic vector potential A ( this-p.10-12,  this-p.12 ).

Quantum field theory needs unreal virtual photons.

QED needs unreal virtual photons that need unreal longitudinal polarization and negative probability.

Real light (or photon ) must be transversely polarized.

But the relativistic QED is unrealistic, needing unphysical virtual photons with non-existent longitudinal polarization ( this-p.3-2 ) and scalar photon ( this-p.5-left-lower ) with unreal negative probability or energy ( this-p.50(or p.49)-last-sentence,  this or this-p.10-6.50,  this-2nd-paragraph ).

This-p.28-last-paragraph says
"virtual photons can be (unrealistically) longitudinally polarized."

This-p.16-2nd-paragraph says
"When charges are present, the (unreal) longitudinal and scalar photons (= unreal negative probability ) provide the Coulomb interaction between the charges and thus appear as virtual particles ( this-p.8 )"

Photons satisfy modified Maxwell equation.

Photons are just unreal math operators expressed in Maxwell equation

Fictitious photons are obtained by quantization of electromagnetic field in Maxwell equation in relativistic quantum field theory or QED where photons are just nonphysical math operators lacking shape (= a^†,  this-p.1~p.12,  this-p.6-10,  this-p.9-10,  this-p.9~ ).

In quantum field theory or QED, the time derivative (= ∂t ) expresses the relativistic energy E, and the space derivative (= ∂x ) expresses the relativistic momentum p by acting on exponential function of e^ikx ( this-p.2 ).

Photons are said to satisfy the massless relativistic energy (= E ) and momentum (= p ) relation (= mass m = 0 ), which corresponds to the massless relativistic Klein-Gordon equation ( this-p.9,  this-p.9-upper,  this-last ) incorporated into classical Maxwell equation.

Quantum field theory's unphysical photons contradict real electromagnetic force.

(Fig.9)  In static electromagnetic field, the time derivative of electromagnetic field (= vector potential A ) is zero, which means photons' energy and momentum in static electromagnetic field are zero, which paradoxically cannot move charged particles.

Photons are unreal, contradict actual phenomena.

Quantum field theory or QED is unreal, unable to explain real electromagnetic field phenomena.

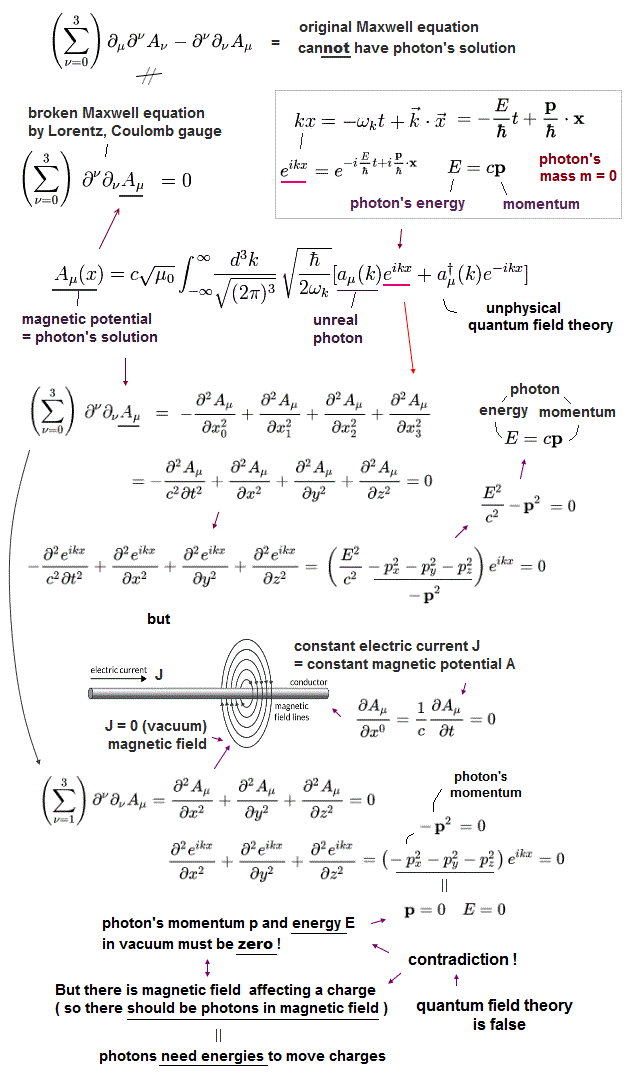
Actually, the relativistic quantum field theory or QED contradicts the real electromagnetic field expressed by Maxwell equation.

In the quantum field theory or QED, the time derivative (= ∂t ) of electric or magnetic potential (= A ) means the relativistic energy E (= photons correspond to massless Klein-Gordon equation,  this-p.5,  this-last ).

Quantum field theory wrongly says the static electromagnetic field contains No photons.

In the static electromagnetic field, this time derivative of electromagnetic field (= fictitious photon's energy ) or (magnetic) potential is zero, which means (virtual) photons' energy E (= ℏω_k,  this-p.11-(31)(32) ) and momentum p (= expressed as the space derivative ) included in the static electromagnetic field must be unrealistically zero.

↑ This unrealistic zero relativistic energy or momentum contradicts the fact that even static electromagnetic field exerts the force and moves the charged particles (= meaning the static electromagnetic energy and momentum, which have the power to move charged particles, are Not zero ).

Relativistic quantum field theory or QED relies on wrong math to explain its (unphysical) photon-electron interaction.

(Fig.10)  QED relies on unphysical photon (= A )-electron (= ψ ) interaction expressed by nonphysical math symbols

Quantum field theory's photons, electrons are unreal.

The unphysical photon-electron interaction in relativistic quantum field theory or QED is based on wrong math.

The unphysical relativistic quantum field theory or QED relies on the abstract electron-photon interaction relation consisting only of unphysical math symbols of illusory photons (= A ) and electrons expressed by Dirac equation ( this-p.4-5 ).

The point is this relativistic QED is based on wrong math to derive this (illusory) interaction relation between (virtual) photons (= vector potential A ) and electrons (= Dirac spinor ψ ).

↑ The unphysical QED interaction between a (fictitious) photon and electrons is expressed just by putting the meaningless math symbols of photon (= A ) and electrons (= ψ ) side by side, which abstract relation cannot clarify real detailed mechanisms.

QED's reliance on wrong math means all QED calculations such as anomalous magnetic moment and Lamb shift are also wrong and illegitimate.

(Fig.11)  Artificial Lagrangian L consisting of electric potential (= φ ), magnetic potential (= A ) and charged particle's velocity (= v ), mass (= m )

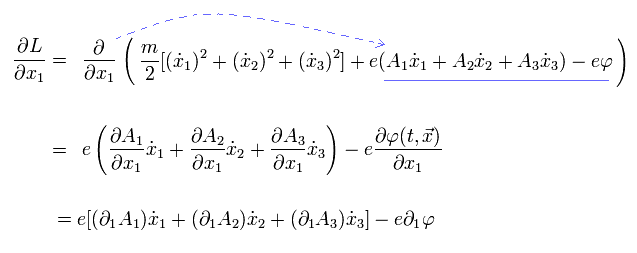
The upper Fig.11 is an artificially-created Lagrangian (= L ) for deriving the (unphysical) interaction between (virtual) photons (= magnetic potential A or electric potential φ ) and electrons (= charge e, velocity of v, mass m ) in QED

Quantum field theory or QED relies on wrong math trick in time derivative of A (= dA/dt ) to derive illusory photon-electron interaction.

(Fig.12)  QED wrong math trick wrongly mixing the static x in vector potential A (= ∂A/∂x ) with the irrelevant moving charge's velocity v = ∂x/∂t in dA/dt.

Derivative of the magnetic potential (= dA/dt ) or external magnetic field falsely includes irrelevant particles' velocity (= dx/dt = v_x ).

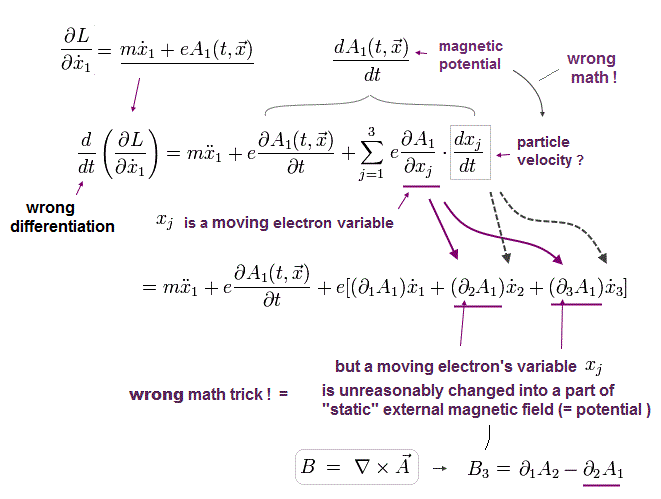
In substituting the artificially-created Lagrangian L into Euler-Lagrange equation, they deliberately use the wrong math trick disproving quantum field theory and QED.

In Fig.12-square, the time derivative of the magnetic potential (= dA/dt ) is wrongly divided into the static space derivative of A (= ∂A/∂x = this x should Not be related to the moving particle's position x of ∂x/∂t = v.  ← but they wrongly treat these two different x as the same x ) and the moving charged particle's velocity (= v = ∂x/∂t ), which causes the serious paradox, so false.

See this-middle,  this-p.3-lower, this-(6),  this-p.3-(18)

(Fig.13)  Artificial-created Lagrangian (= L ) can obtain electromagnetic force ?

By inserting the artificially-created Lagrangian (= L ) into Euler-Lagrange equation, they (wrongly) claim the electric (= E) and Lorentz magnetic (= B ) force expressed as electric or magnetic vector potentials on the charged particle (= charge e, mass m, velocity v ) can be obtained.

(Fig.14)  Artificially-created QED Lagrangian is wrong, unable to express the static electromagnetic field.

QED electromagnetic force uses wrong math.

In case of the static magnetic field where the time derivative of the magnetic potential is zero (= dA/dt = 0 ), the artificially-created electromagnetic Lagrangian L cannot obtain the real (electro-)magnetic field (= B ) due to the wrong math trick.

As shown in Fig.14-lower, in the static magnetic field (= dA/dt = 0 ), the real magnetic field B_z consisting of two magnetic vector potentials of A_x and A_y cannot be obtained ( this-p.4 ).

(Fig.15)  Relativistic quantum field theory or QED is wrong, relying on wrong math trick to derive its illusory photon-electron interaction.

QED is unreal, wrong.

QED's photon-electron interaction is just nonphysical math lacking reality.

From the artificially-created electromagnetic Lagrangian L and Hamiltonian H replacing the momentum p → p-eA (= A is magnetic potential,  momentum p is the space derivative, this-8.3.1.1 ) based on wrong math, physicists tried to obtain the illusory interaction between virtual photon (= A ) and Dirac's electron (= ψ ) in QED ( this-p.2.p.10-C,  this-p.1-p.6,  this-p.24,  this-last,  this-p.1-last ).

QED relying on this wrong math for deriving artificial electron-photon interaction relation means all (dubious) calculations of QED such as anomalous magnetic moment and Lamb shift are wrong, too.

Feel free to link to this site.