
Top page ( Quantum mechanics is wrong )
Helium Schrodinger
(Fig.1) Quantum mechanics gives unreal hydrogen model with spin ↓

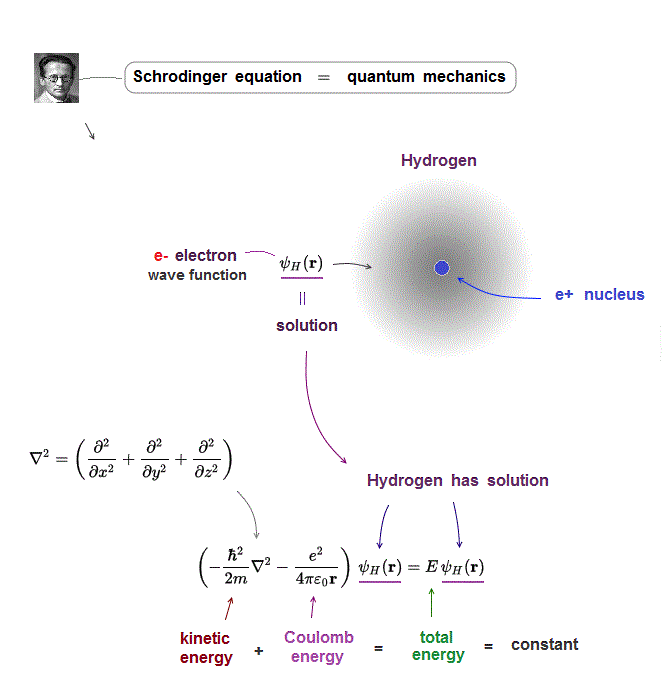
Bohr model first succeeded in explaining hydrogen energy levels, and was replaced by quantum mechanics in 1920s.
Quantum mechanics relies on Schrodinger equation in calculating atomic energies.
Atomic models by Schrodinger equation is very unrealistic
Surprisingly, quantum mechanics requires that s orbitals (= ground state ) have zero angular momentum ( this p.2 ). ←Electrons often hit nucleus ?
Furthermore, quantum mechanics needs nonsense spin, which spinning must far exceed light speed to generate experimental magnetism.
(Fig.2) No solution → just "choose" trial functions ! = useless

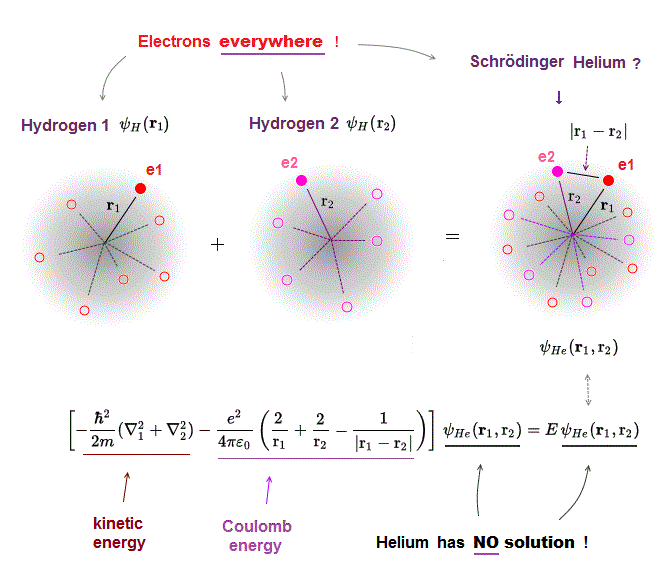
Schrodinger equation of two-electron helium contains interelectronic Coulomb energy. So it has No solution of helium.
All other multi-electron atoms including H2+ molecule ion have No exact solution. Then how does quantum mechanics deal with multi-electron atoms ?
Surprisingly, they just choose artifical trial function as "imaginary" solution.
"Choosing" convenient hypothetical solution out of infinite choices means Schrödinger equation has no ability to predict multi-electron atoms.
And it's impossible to try infinite kinds of trial wavefunctions and find the one giving the lowest energy in them.
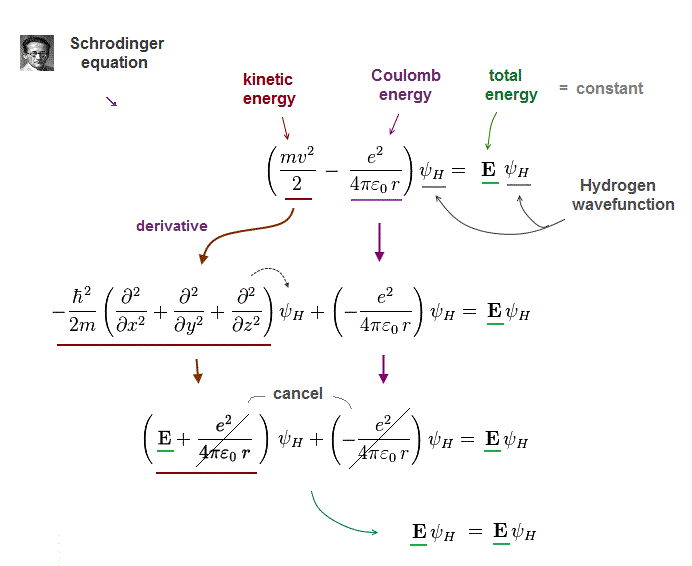
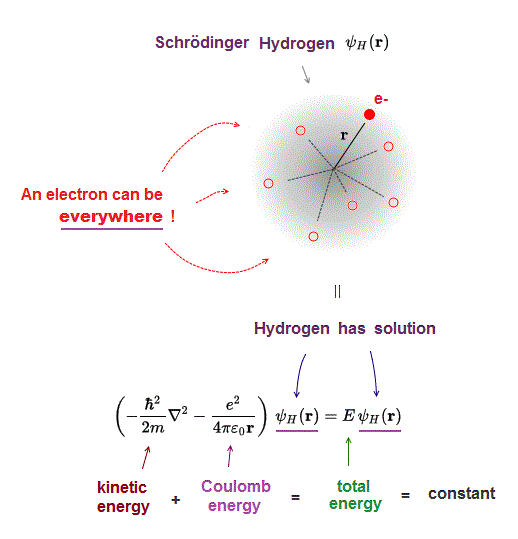
(Fig.3) Hydrogen, the sum of kinetic and Coulomb energies is conserved.
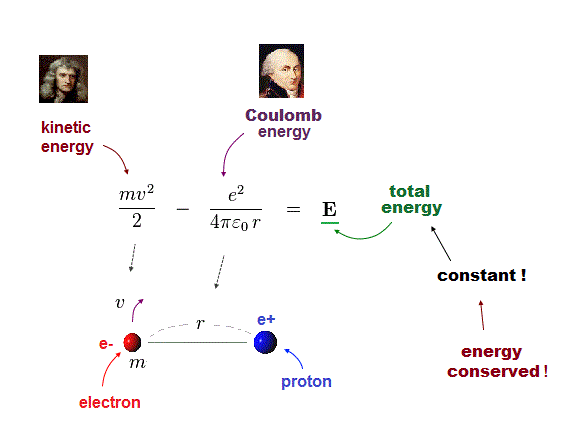
Total energy E, the sum of kinetic energy and Coulomb potential energy, must be always conserved (= E is a constant value ).
Also in Schrodinger equation of quantum mechanics, this total energy must be conserved in all atoms ( this p.9 ).
Fig.3 shows Hydrogen atom consisting of an electron and a proton attracting each other by Coulomb force.
(Fig.4) One-electron Hydrogen atom has the exact solution.
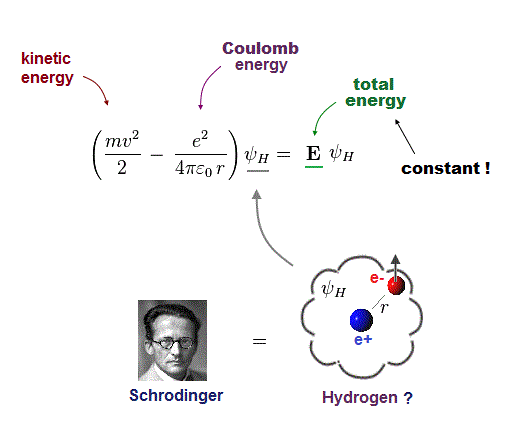
Also in Schrodinger equation of quantum mechanics, the atomic total energy E is the sum of kinetic energy and Coulomb energy between a nucleus and an electron.
Under the constant total energy E, Schrodinger equation can be solved in hydrogen atom.
(Fig.5) Law of conserved total energy E is valid only in Hydrogen !
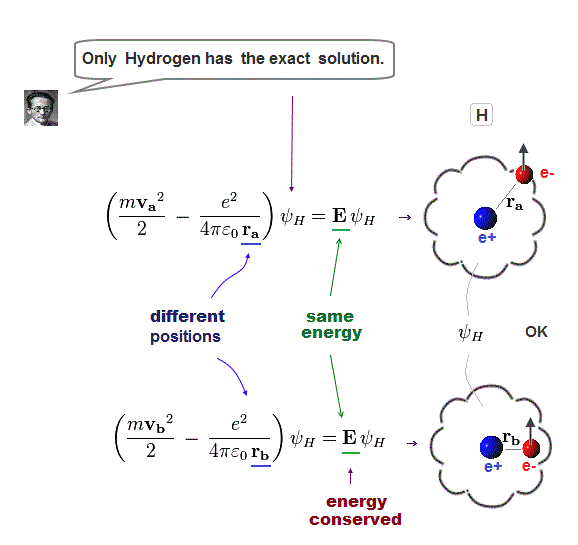
It is known that one-electron Hydrogen is the only atom which Schrodinger equation can solve.
NO other atoms such as Helium have their solutions in quantum mechanics due to their interelectronic Coulomb term.
Having the solution means we can find the constant total energy E conserving the sum of kinetic and Coulomb energy in all electron's positions.
This law of energy conservation is applied only to solvable one-electron hydrogen atom in quantum mechanics.
All other unsolvable atoms violate this basic law of "energy conservation", so their physical model don't represent realistic atoms.
(Fig.6) Double-slit, Davisson-Germer proved electron's de Broglie wavelength.
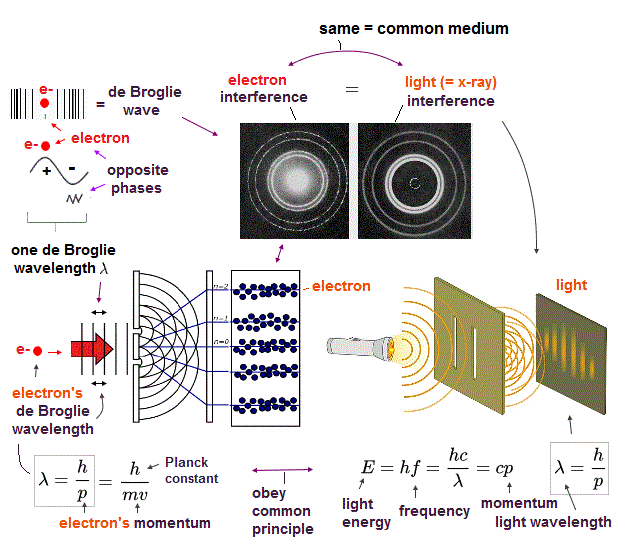
In de Broglie relation, electron's wavelength λ is given by λ = h/mv, where m and v are electron's mass and velocity.
This important matter-wave relation was confirmed in various experiments such as doube-slit, Davisson-Germer and this.
So there is No room for doubt that this de Broglie wave is true.
Electron's de Broglie wave is a real concept, which must be used in any atoms.
Of course, Schrodinger equation in quantum mechanics also uses this de Broglie relation.
(Fig.7) m and v are a electron's mass and velocity.
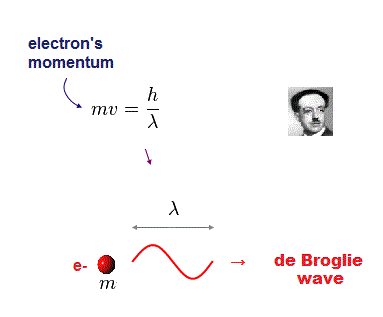
According to de Broglie relation, each particle's momentum (= mv ) is equal to h/λ ( h is Planck constant, λ is de Broglie wavelength ).
(Fig.8) Momentum operator + quantum wavefunction (= de Broglie ).
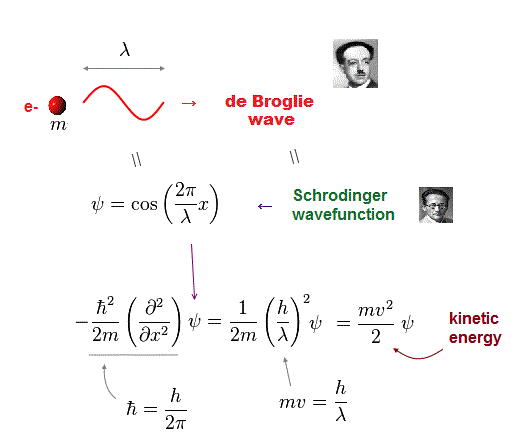
Quantum mehanics also depends on this de Broglie wave as wavefunction. By applying momentum operator to quantum wavefunction, we get usual kinetic energy.
(Fig.9) Total energy = de Broglie momentum + Coulomb.
Schrodinger equation of Hydrogen describes electron's kinetic energy using de Broglie wave relation.
Under conserved (= constant ) total energy E, Schrodinger equation of Hydrogen atom can be solved and find exact solution (= ψH ).
(Fig.10) Schrodinger's hydrogen obeys n × de Broglie wavelength.
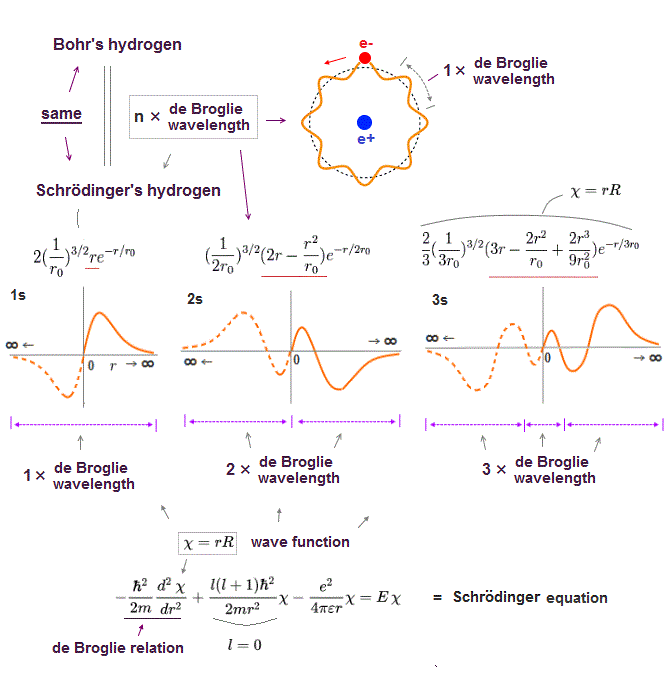
It's a famous story that old quantum orbits become an integer times de Broglie wavelength.
In fact, Schrodinger 's hydrogen wavefunction also satisfies this integral multiple of de Broglie wavelength ( this p.9 ), though they don't admit it openly.
Without this de Broglie boundary condition, hydrogen ground state energy can get lower than experimental value, unlimitedly !
The point is this de Broglie condition (= an integer times wavelength ) is valid only when Schrodinger equation can be solved exactly like in hydrogen atom.
So in all other unsolvable atoms, Schrodinger equatin disobeys not only energy conservation but also de Broglie condition ! This is the reason they are useless.
(Fig.11) Total energy E is unchanged in different electron's positions (= ra, rb ).
Only Hydrogen atom can be solved by Schrodinger equation, which means hydrogen has its exact wavefunction (= ψH ) and constant ground state energy (= E ).
Wherever the electron exists inside a hydrogen, it gives the same total energy E (= kinetic + Coulomb energies ) due to energy conservation law.
(Fig.12) Helium cannot be solved = NO constant common total energy E
Other atoms such as Helium have NO solutions in quantum mechanics.
It means we can find neither their exact wavefunction (= ψHe ) nor total energy E.
(Fig.13) Schrodinger equation has NO ability to find exact "constant" energy !

To describe realistic atomic behavior, we have to find exact electrons' states obeying total energy conservation law.
But quantum mechanics cannot solve multi-electron atoms, meaning NO constant ground state energy E can be found !
So as long as we depend on Schrodinger equation, its multi-electron atoms disobey total energy conservation (= constant E ), which doesn't describe real phenomena.
(Fig.14) Any approximate solutions in Helium violate energy conservation !
Solvable Hydrogen atom can find its exact wavefunction and total energy E, which is common in any electron's positions.
So the sum of kinetic and Coulomb potential energies in hydrogen's electron always becomes constant due to energy conservation.
It's impossible to solve Schrodinger equation for milt-electrons such as Helium.
This means there is NO "constant common energy E" in helium
Even if you use any approximate (= fake ) helium wavefunctions, they don't obey total energy conservation under common total energy E, so meaningless.
(Fig.15) Choose trial He function → Integral (= NOT solve ) → fake energy.
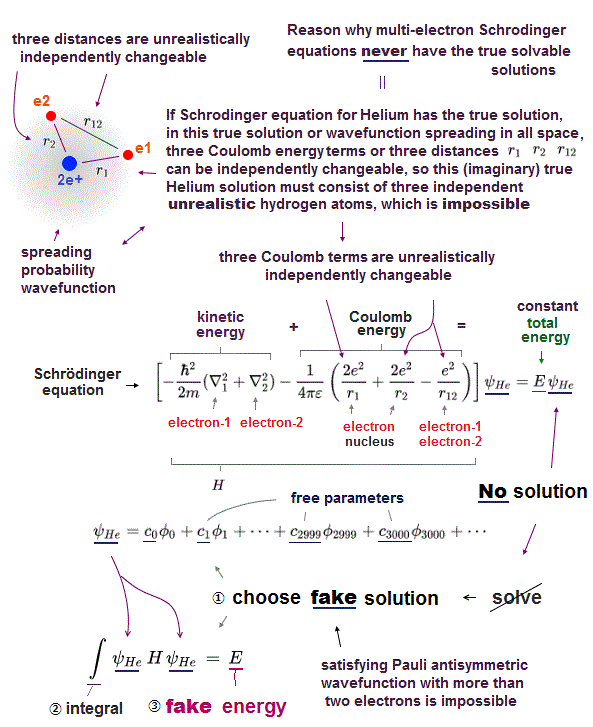
Multi-electron atoms such as Helium cannot be solved due to their interelectronic interaction. They just choose a trial (= fake ) function out of infinite choices.
Putting Schrodinger equation between this chosen trial helium functions (= ψHe ), they integrate them over all space, instead of solving them.
The present quantum mechanics adopts this fake total energy E as approximate Helium energy. But they include serious defects.
Because chosen tiral function is NOT a solution of kinetic + Coulomb energies, which disobeys total energy conservation, so unreal atomic models.
(Fig.16) ↓ Variational method of Helium is impractical.
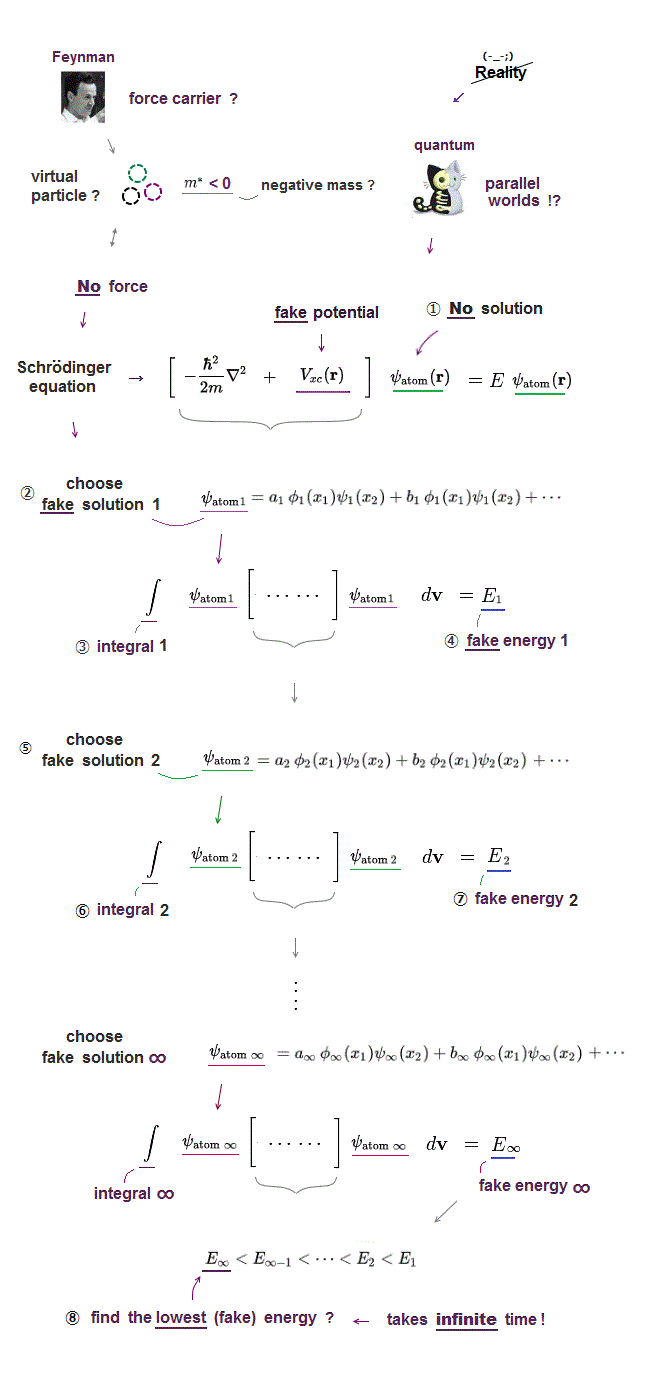
In the present useless quantum mechanics, they just guess and choose some trial function and adjust their free parameters to obtain desired energies.
The problem is there are "infinite free choices" in this trial wavefunctions, so we cannot try all possibe wavefunctions to compare their energies.
It means finding the lowest ground state energy by trying infinite choices is impossible in quantum wavefunction.
All these trial function don't satisfy the total energy conservation, so "fake" energy, after all, meaningless.
The present use of "finite" basis set as approximate function never represents truth ( this p.4 )
(Fig.17) Because approximate helium functions are NOT a true solution.
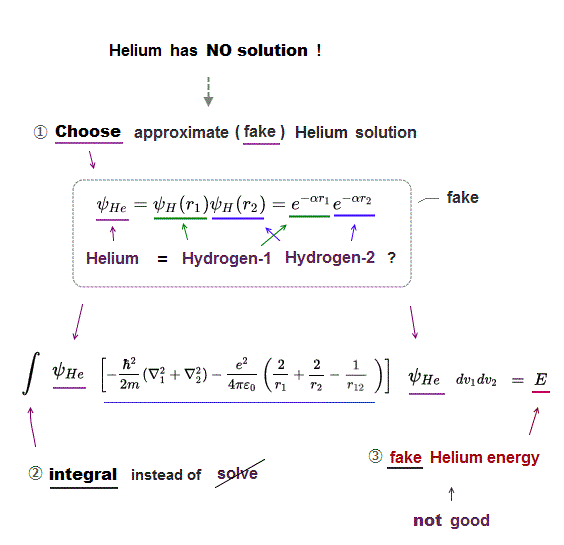
In Schrodinger equation, all they can do is integrate approximete trial functions instead of solving them.
This appoximate total energy E is a fake energy, which is just a collection (= average ) of different energies in different electrons' positions.
For example, when two electrons of helium are at positions of ( r1a, r2a ), their total energy E is a different value from when they are at ( r1b, r2b ).
Of course, if constant total energy E cannot be used, Schrodinger equation has NO ability to predict any real atomic energies and behavior, so useless.
(Fig.18) Stick to unsolvable Schrodinger equation = NO progress, forever !

As long as we stick to Schrodinger equation of quantum mechanics, our science remains useless, forever.
It's impossible to try infinite kinds of possible choices as approximate wavefunction.
Furthermore, unsolvable Schrodinger equation violates two basic postulates, total energy conservation and de Broglie wave.
This is the reason why quantum mechanics cannot predict any actual energies and phenonema in multi-electron atoms, and are useless.
(Fig.19) Why Schrodinger equation cannot handle multi-electron atoms ?

Schrodinger equation is also based on two postulates such as Coulomb force and de Broglie wave relation.
In the only solvable one-electron hydrogen, total energy E is conserved as the single common value in any electron's positions (= Coulomb ).
And its solution naturally obeys an integer times de Broglie wavelength as boundary condition (= de Broglie ).
It is quite natural that we can predict any values even in multi-electron atoms obeying these basic common postulates.
The problem is quantum mechanics violates these two basic postulates in multi-electron atoms except hydrogen !
No solution in multi-electon atoms means we cannot find the single common energy value in any electrons' positions.
In the same way, No solution means the "integer times de Broglie wave rule" is ignored and violated.
So violating two basic postulates is the main reason quantum mechanics cannot predict any values in multi-electron atoms.
(Fig.20) "Choose" trial functions → integral over all space.

Here we explain why these "chosen" wavefunction cannot give true ground state energy of helium.
After choosing some trial wavefunction of unsolvable atoms, they integrate them over all space, and get, what they call, approximate total energy E'.
The point is this approximate energy E' is just an average energy in a collection of different energies depending on different electrons' position.
Originally, the sum of kinetic and potential energy in any electrons' positions must be equal to the single common ground state energy E.
But "unsolvable" multi-electron wavefunctions don't satisfy this basic condition.
So, this "average" energy E' does Not mean the single common ground state energy in any positions of helium.
(Fig.21) We must use experimental data to predict "real concept" !
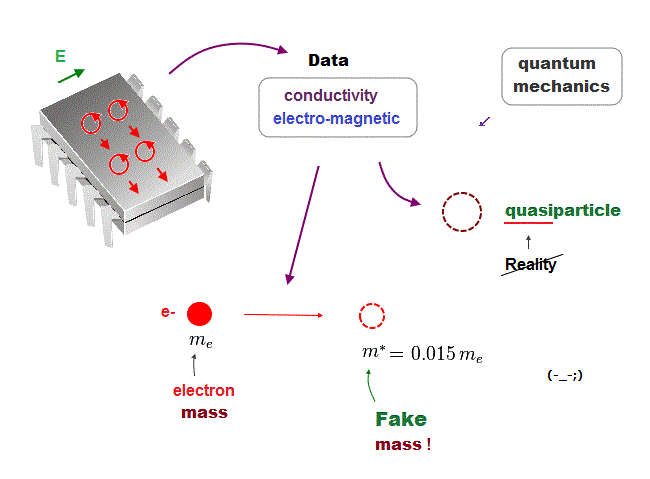
In the present quantum mechanics, even when we get some new experimental data, we cannot use them to clarify real mechanisms !
Instead, quantum mechanics forces us to use these data to create artificial quasiparticle, effective mass .. So our science stops its progress.
This is a very serious problem. We must address it immediately not to increase more educational victims under false science.
(Fig.22) Coulomb energy conservation and an integer times de Broglie wavelength.
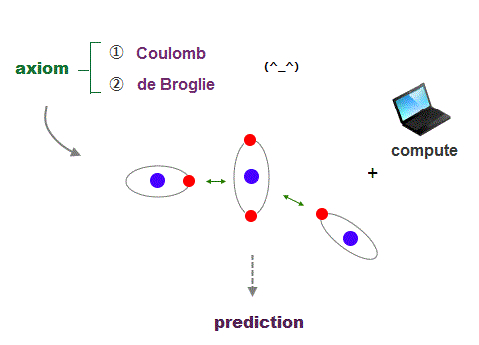
It's quite natural that if we keep basic postulates, we can predict any physical values ( with the help of modern computer ).
These two postulates are Coulomb energy conservation ( in any electrons' positions ) and an integer times de Broglie wavelength generating Pauli force.
There is No way other than computing each Coulomb force and changing electrons' position in orthodox way to keep the single common ground state energy.
Of course, to obey an integer times de Broglie wave rule, this computing method using concrete orbits is the only one.
So the first thing for researchers to do is determine the more precise electronic motion model step by step, comparing experiments and the model's prediction.
I'm sure this realistic model based on two postulates will contribute to curing fatal diseases such as cancer, ALS, dementia someday.

2016/4/22 updated. Feel free to link to this site.