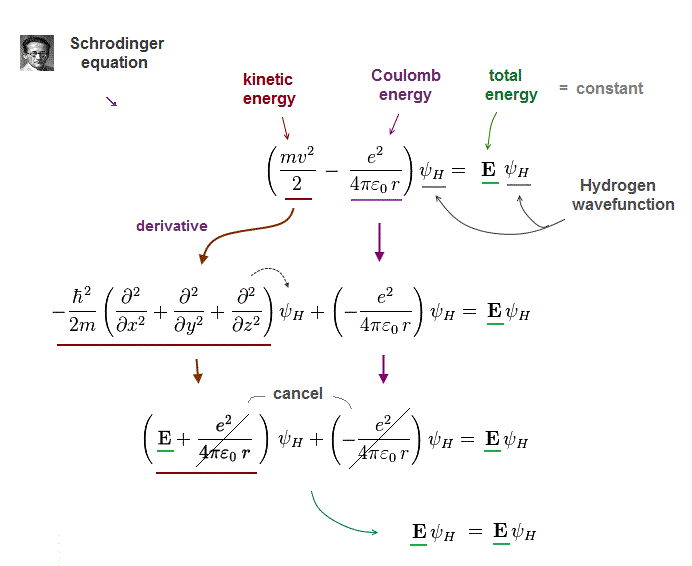
(Fig.1) Kinetic + potential energies = total energy E

Under the present science, Schrödinger equation in quantum mechanics is the only tool to calculate atomic energy.
Unfortunately, Schrödinger equation can solve only one-electron hydrogen atom, cannot deal with other multi-electron atoms.
Total energy E is the sum of an electron's kinetic energy and Coulomb potential energy in Schrödinger equation.
Of course, this total energy E must be conserved (= constant ) in every electron's position.
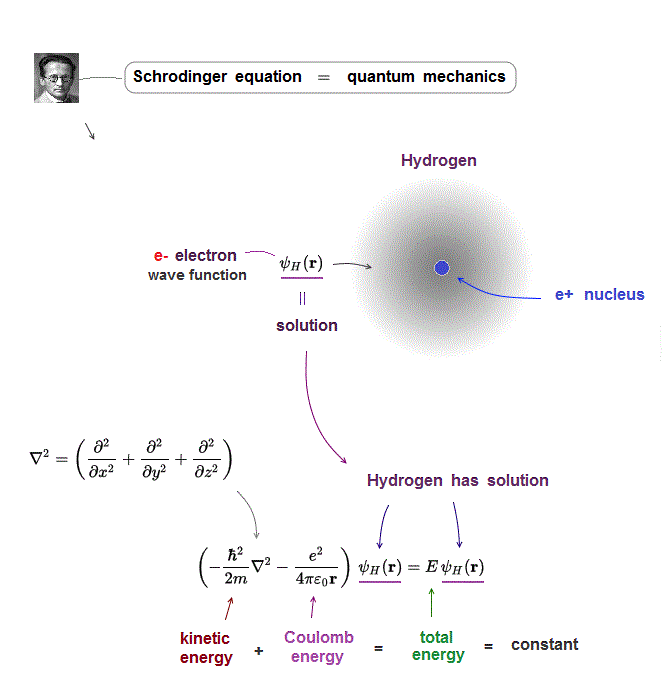
(Fig.2) ↓ Only one-electron hydrogen has solution.
In quantum mechanics, only one-electron hydrogen has solution.
When you insert one of these hydrogen solutions (= wave function ) into Schrödinger equation, you can get an identical equation.
An identical equation means that total energy E is common and constant in every electron's position r in hydrogen.
(Fig.3) Schrödinger equation for Helium has NO solution.

One-electron hydrogen is the only atom which quantum mechanics can deal with.
There is NO exact solution in multi-electron atoms such as Helium.
It means you cannot find any Helium solution (= ψHe ) which satisfies an identical equation under the common energy E.
(Fig.4) ↓ Helium approximate quantum method is just fake !
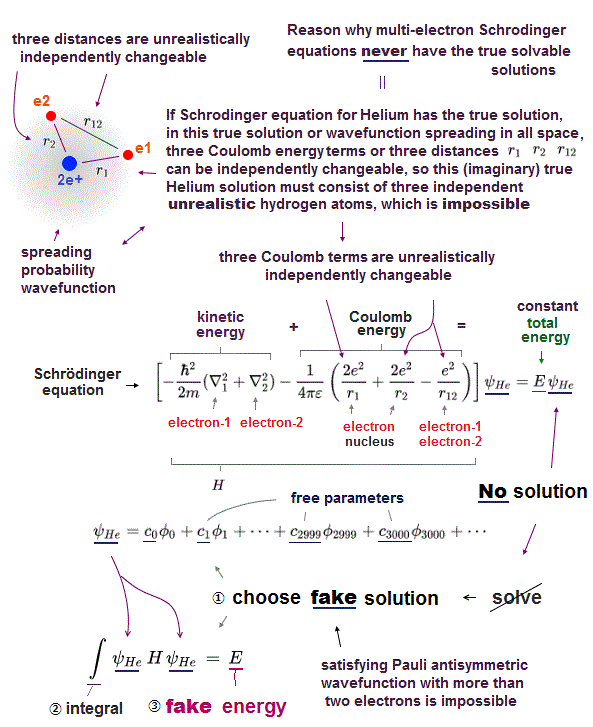
In Helium atom, the first thing you do is choose trial function as "fake" Helium solution, and insert it into Schrödinger equation.
After putting Schrödinger equation between two tial function (= ψHe ), you integrate it instead of solving it, because you cannot solve it.
The total energy E by this method is not true Helium energy.
You just repeat this ( choose different trial functions → insert → integral ) until you can get convenient fake energy.
You have to try infinite different trial functions as Helium fake solution and compare them to find the solution which gives the lowest ground state energy E.
But of course, it's impossible to try infinite kinds of trial function to find the lowest Helium energy E. So Schrödinger equation is useless in Helium.
(Fig.5) Schrödinger equation with NO solution has NO approximation !
They often use the word "approximate method" in unsolvable Schrödinger equation for Helium, this is completely the wrong use of the word.
Because if we cannot solve some Schrödinger equation, there is substantially NO "approximate" solution.
There are only two options: solvable or unsolvable in quantum mechanics !
The upper variational method using trial function is completely different thing !
Even if you can try infinite different trial function as Helium solution, it's impossible to find the true solution like hydrogen.
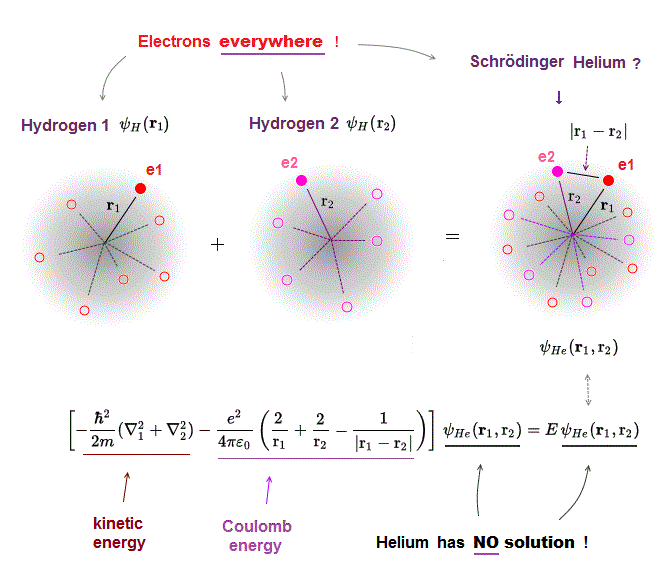
If there was true Helium solution satisfying an identical Schrödinger equation, three potential energy terms must be cancelled out independently !
Each independent Coulomb energy term cannot give true atomic energy specific to each different atom.
(Fig.6) They just choose "fake solution" from infinite choices ← useless !
After using atomic force microscope and detecting the slight force of a single atoms or molecule, we need to interpret those forces using some atomic model.
Unless we can explain each single atomic force, we cannot move forward to the next step of utilizing multi-atomic bahavior.
The problem is that there is the only useless quantum mechnaics (= Schrödinger equation ) as a tool to interpret these atomic data, now.
Quantum mechanics have NO exact solution in multi-electron atoms, so they just choose fake solution from infinite choices, meaning no power to predict anyhing.
In atomic force microspopy, they use densisty functional theory (= DFT ), which is a further approximation of quantum mechanics, so more incorrect and useless.

2017/5/26 updated. Feel free to link to this site.