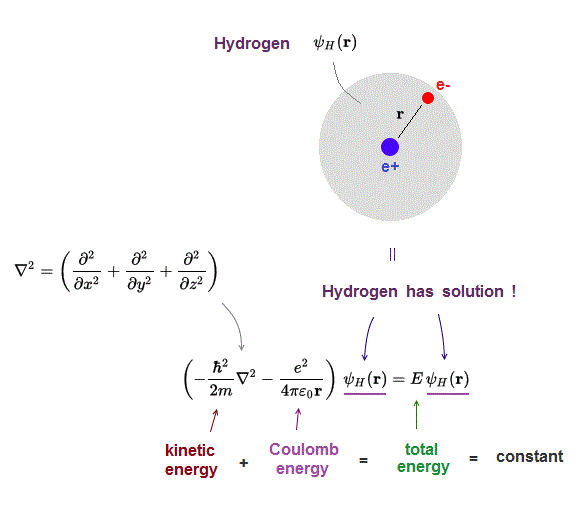
(Fig.1) Schrödinger equation for hydrogen atom = a proton + an electron

Only Schrödinger equation for one-electron hydrogen atom can be solved and has exact solution.
Schrodinger equation gives the constant total energy equal to the sum of kinetic and potential energies.
(Fig.2) ↓ Schrödinger equation Helium = two electrons (e-) + one nucleus (2e+)

Schrödinger equation for multi-electron atoms such as Helium cannot be solved ! Helium atom consists of two electrons ( e- ) and one nucleus ( 2e+ ).
Helium's total energy E should be the sum of kinetic energy and Coulomb potential energy.
r1 ( r2 ) is the distance between the nucleus and electron 1 ( electron 2 ).
|r1 - r2| is the distance between two electrons
(Fig.3) No Helium solution → choose "fake" solution for Helium.

Schrodinger equation for Helium has NO exact solution, so all physicists can do is choose "fake" trial wavefunction for Helium "temporary" solution.
There is NO limitation and NO regulation in choosing these fake approximate solutions. You can choose any forms of fake solution out of infinite choices !
So physicists can choose convenient approximate solution giving experimental result, as they like. It means Schrodinger equation is meaningless and useless.
(Fig.4) If increase solution's terms and kinds, it can approach true solution ?

Physicists just choose "fake" Helium solution ( this p.9, this p.2 )
If we try all kinds of Helium approximate solutions, we can find true Helium solution ( which will include infinite terms ) ?
Unfortunately, no matter how many terms you increase as Helium "fake" solution, you can Never get true Helium Schrödinger solution !
(Fig.5) Three Coulomb energy terms can be cancelled by kinetic terms ?
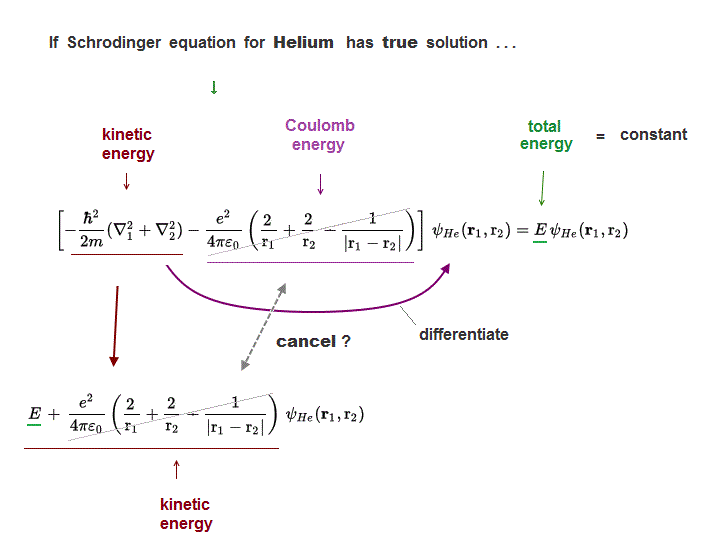
In Helium true solution, its three Coulomb energy terms must be completely cancelled out by their corresponding kinetic energy terms to give "constant" total energy E.
Operator for kinetic energy differentiates Helium wavefunction, and gives kinetic energy terms cancelling corresponding Coulomb energy terms ?
Unfortunately, we cannot find those Helium true solution !
(Fig.6) ↓ Three Coulomb energy terms (= ①, ②, ③ ) are independent ?
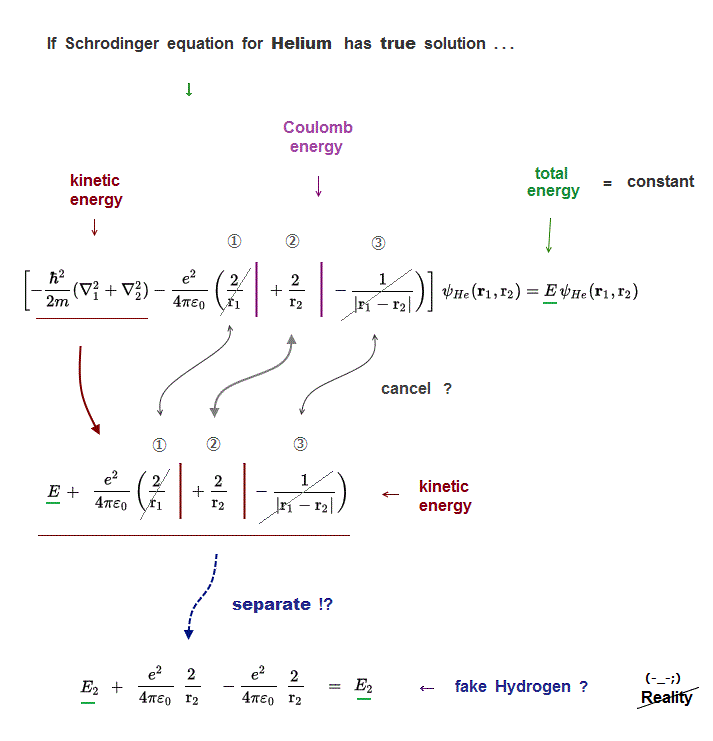
Each of three Coulomb energy terms (= ①, ②, ③ ) must be cancelled out independently by its corresponding kinetic energy term.
Because "true Helium solution" must give "constant" Helium total energy E.
But those solutions ( even if you luckily find ) cannot describe true Helium atom !
(Fig.7) Helium true energy → three Coulomb terms must be independent !?

If Schrodinger equation for Helium has "true" solution, all three Coulomb energy terms must be completely cancelled out by kinetic energy.
It means these three different Coulomb terms can be independently canceled by its corresponding kinetic energy term → three "fake" hydrogens !?
So in true Helium solution (= if it exists ), Helium can be divided into three "fake" hydrogen, one of which is unreal hydrogen (= ③ is electron-electron hydrogen ? )
(Fig.8) So three Coulomb energy terms must be independent in Schrödinger.
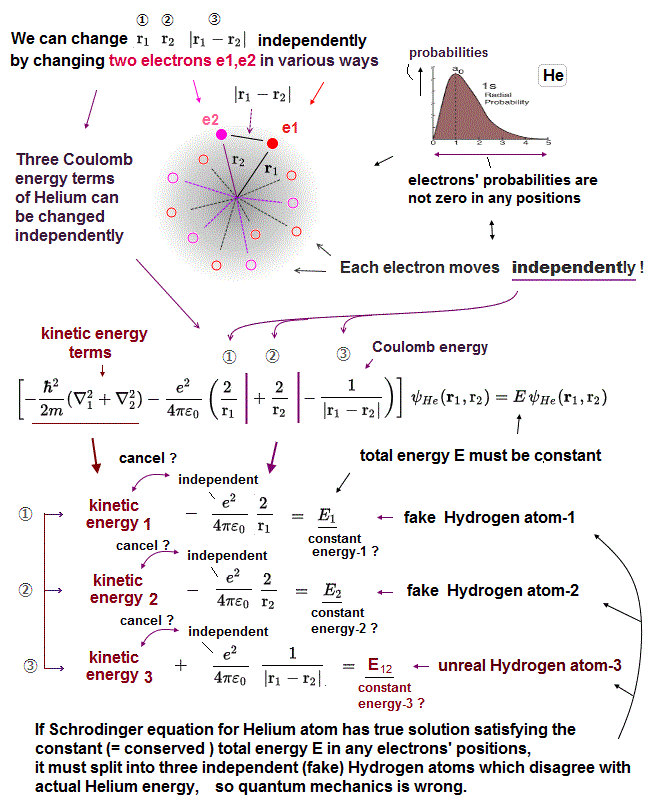
Schrödinger wave function is spreading all over the space, and their electrons can exist everywhere.
If Helium consists of two hydrogen wave functions as Schrödinger argues, each of three Coulomb terms can be varied "independently".
In Fig.8, we fix r1, r2, changing only interelectronic distance |r1 - r2| which changes only Coulomb energy term (= ③ ) between two electrons.
In the same way, we can change only r1 ( or r2 ), fixing r2 ( or r1 ) and |r1 - r2|.
Each "independent" Coulomb energy term cannot express the property of the "whole atom" specific to different atoms. So Schrodinger equation gives "wrong" atoms.

2017/1/13 updated. Feel free to link to this site.