Home page ( Quantum mechanics is false ← 6/15/2025 )
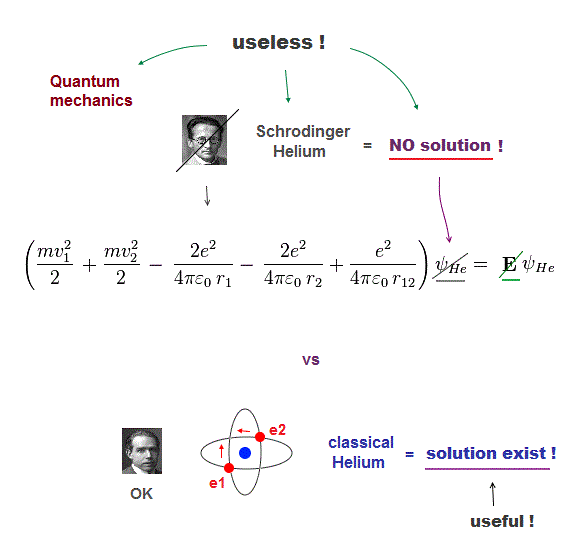
(Fig.1) Only classical model can give exact solution in multi-electrons

Despite the media-hype, the present basic physics remains useless, a waste of money, pursuing unreal quasiparticle, parallel worlds in quantum "scam" computer.
The basic reason for "deadend" science is Schrodinger equation is useless, cannot solve multi-electron atoms. So all other applied science remains useless, forever.
Here we prove Schrodinger equation is pursuing "illusory" solutions in multi-electron atoms, and only classical model can have exact atomic solution (= model ).
(Fig.2) Total energy E is "constant" and conserved in hydrogen
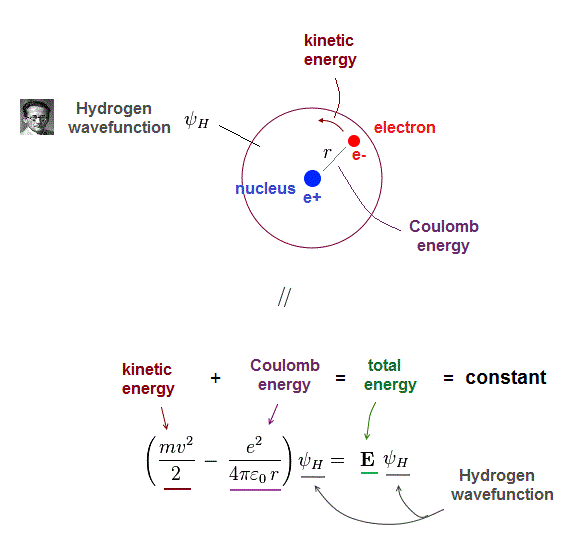
One-electron hydrogen atoms is the only one Schrodinger equation can solve. Total energy E is the sum of electron's kinetic energy and Coulomb potential energy.
Of course, the total energy E must be conserved which means E is a "constant" (= NOT viriable ) value.
(Fig.3) Kinetic energy term in Schrodinger equation = derivative
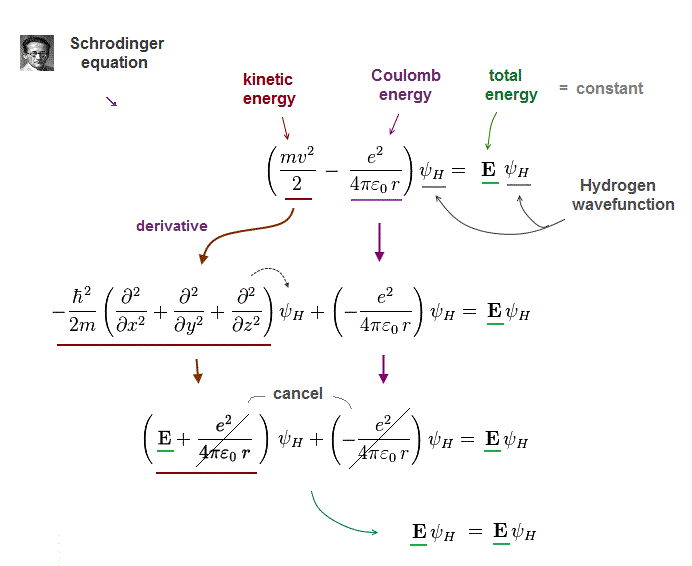
To obtain "constant" total energy E, variable Coulomb energy terms must be cancelled out by kinetic energy terms.
In Schrodinger equation, electron's momentum (= kinetic ) term is expressed as "derivative" acting on wavefunction ψ
After this momentum operator acts on wavefunction, it gives "variable" kinetic energy terms which just cancel "variable" Coulomb energy terms.
As a result, the sum of kinetic energy and Coulomb energy terms gives "constant" total energy E.
(Fig.4) Kinetic energy operator (= ∇ ) acts on wavefunction ψ
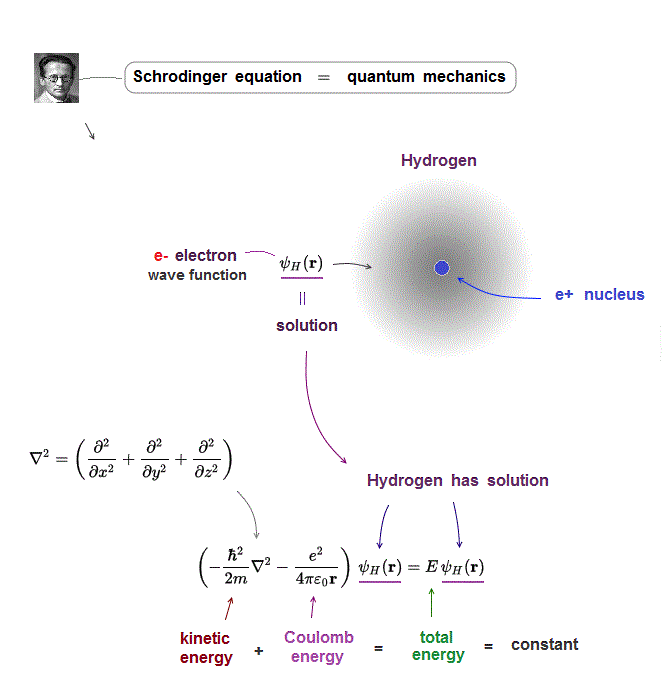
In Schrodinger equation, electron's momentum (= kinetic energy ) is based on de Broglie waves which are expressed as "derivative".
Kinetic energy is the square of electron's momentum (= derivative ∇ ), so it is denoted by the second-derivative (= ∇2 ).
(Fig.5) r12 = distance between two electrons 1, 2
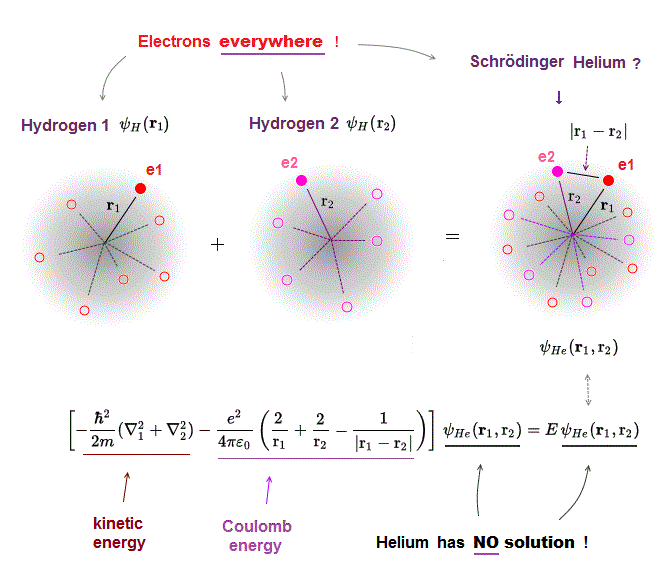
Schrodinger equation in multi-electron atoms includes Coulomb energy term between two electrons.
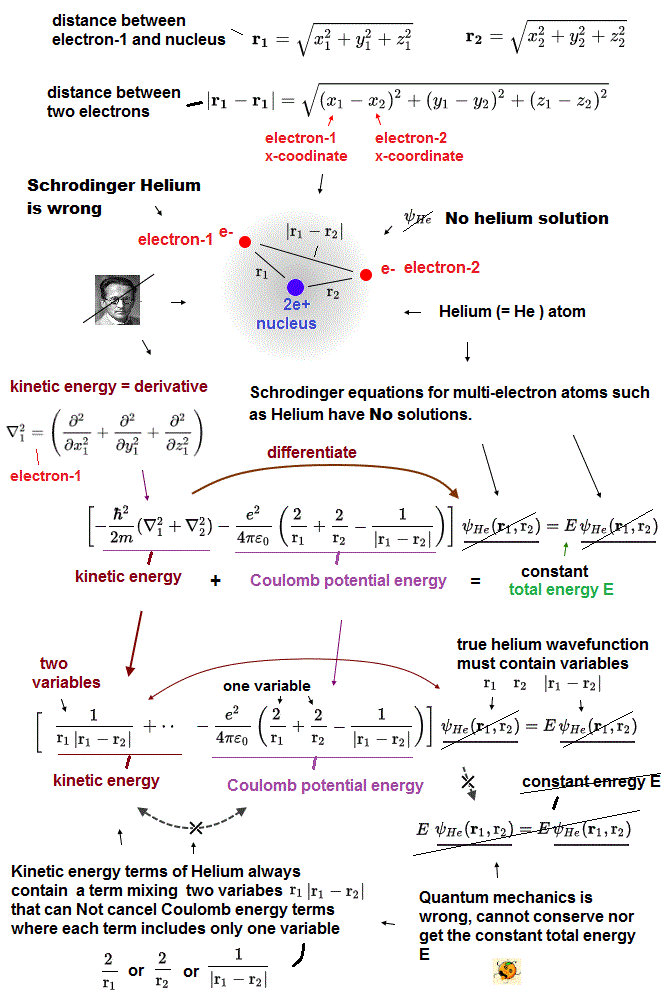
r1 ( or r2 ) means the distance between electron 1 ( or 2 ) and helium nucleus. r12 means the distance between two electrons.
If the exact helium solution existed, it must give "constant" total energy E in any electrons' positions. But NO helium solutions exist in Schrodinger equation.
(Fig.6) There are NO solutions giving "constant" total energy E in helium

Also in helium atom, total energy E must be conserved and constant. To do so, all three "variable" Coulomb energy terms must be just cancelled out by kinetic energy terms.
But we cannot find those exact Helium solutions (= ψHe ) to meet this condition of "constant" total energy E in Schrodinger equation.
It means Schrodinger equation and quantum mechanics are false.
(Fig.7) Total energy E must be "constant", even when only r12 changes.
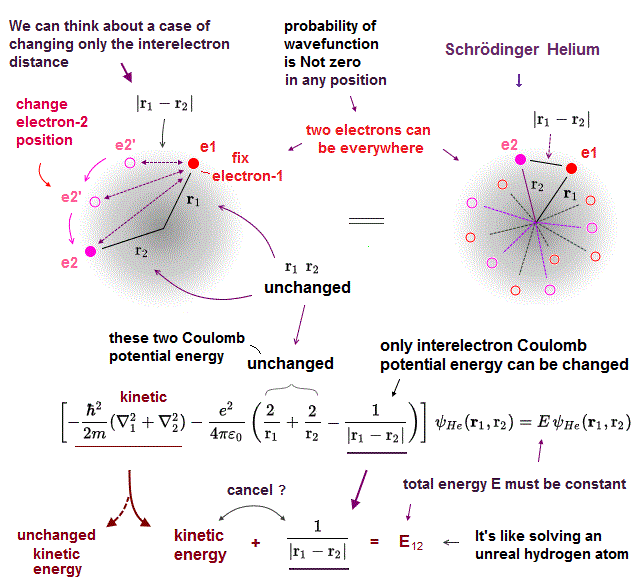
Helium atom cannot be solved exactly. Instead they often choose two hydrogen wavefunctions ( of electrons 1 and 2 ) as "approximate" helium wavefunction.
Different from classical model, the electron's wavefunction in Schrodinger equation always spread all over the space.
Here we fix two variables r1, r2 (= distance between each electron and nucleus ), and change only the distance (= r12 ) between two electrons in helium wavefunction.
If this is the exact helium solution, all these cases (= changing interelectronic r12 ) in them must give the common same total energy E.
But it's impossible to find those exact helium solutions.
(Fig.8) When only interelectronic r12 is changed ..
When you change only interelectronic distance (= r12 ), fixing r1, r2 in helium wavefunction, Only Coulomb energy (= 3rd term ) between two electrons changes.
To get the constant, common total energy E, this variable interelectronic Coulomb energy term must be cancelled by corresponding kinetic energy term.
Here we change only interelectronic distance (= r12 ).
It means corresponding kinetic energy term ( including only r12 ) must cancel only interelectronic Coulomb term independently from other terms including r1, r2 !
Finding these solutions is absolutely impossible.
(Fig.9) Each of three Coulomb energy terms is "independent" from each other ?
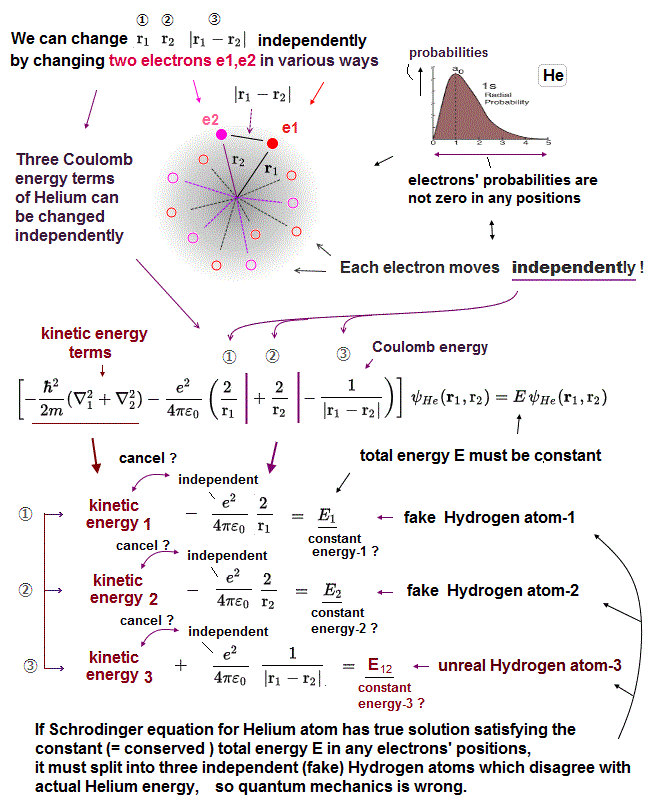
Helium contains three Coulomb energy terms ( ① = between electron1 and nucleus, ② = between electron2 and nucleus, ③ = between two electrons ).
All these three Coulomb terms are separated independently. So corresponding kinetic energy terms have to cancel each term independently.
For example, Coulomb energy between two electrons (= ③ ) must be cancelled by kinetic energy term including only variable r12 (= NOT including other r1, r2 ).
In actual atoms, it's impossible to deal with only interelectronic Coulomb energy independently from other Coulomb energies such as between nucleus and electrons.
(Fig.10) In multi-electron atoms, each energy term must be independent !?
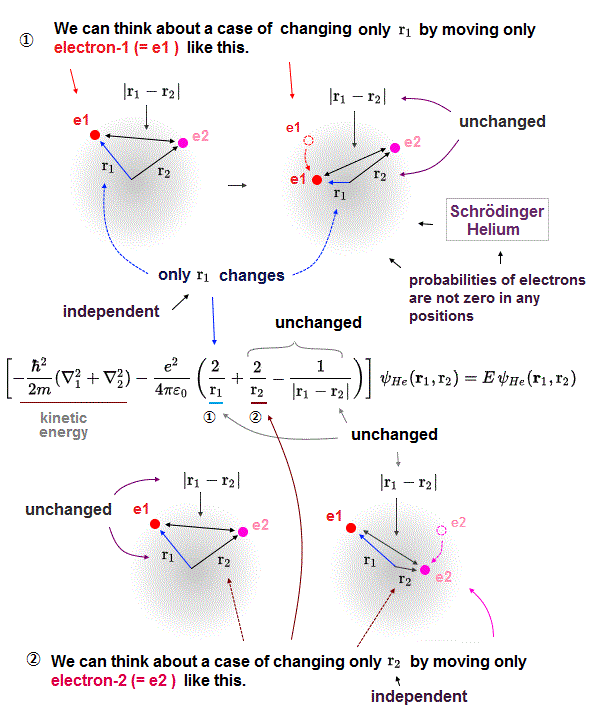
Here is the reason why Schrodinger equation in multi-electron is unrealistic and can never give exact solution.
"Exact" solution (= wavefunction ) must give "constant" total energy in any electron's positions and any interelectronic distances.
To do so, all three "variable" Coulomb energy terms must be cancelled by their corresponding kinetic energy terms completely.
But all these three Coulomb terms are separated and independent from each other, and each has a different variable in Helium Schrodinger 's equation.
It means corresponding kinetic energy and total energy (= E3 ) related only to interelectronic distance (= r12 ) must be independent from other energies !
If so, we can pick out only interelectronic Coulomb term from the whole atoms. This is unrealistic and impossible.
(Fig.11) In real atoms, r1, r2 change as a function of r12 = NOT independent
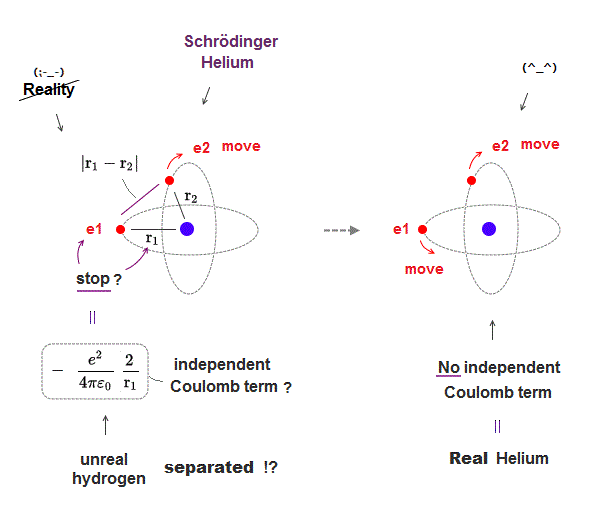
In actual multi-electron atoms, three Coulomb terms in Helium can NOT be independent from each other.
As shown in Fig.11, when two electrons come closer to each other (= r12 is shorter ), the distance between nucleus and each electron is longer (= r1, r2 are longer ).
So each variable are NOT independent from each other, but a "function" of other variables. This is a realistic atomic model.
Schrodinger wavefunction spreading all space must cancel each Coulomb term independently, which is unrealistic, and the reason it has NO exact solution.
(Fig.12) ↓ Unrealistic multi-electron Schrodinger equations

Different from actual multi-electron atoms ( with electron's "orbit" ), Schrodinger's wavefunction always spread all over the space.
This property makes it impossible to solve Scchrodinger equation in multi-electron atoms.
To get the constant total energy E, each Coulomb energy term with different variable must be treated and cancelled independently.
It means in any atoms, only interelectronic Coulomb energy term can be picked up from other terms, and is given "independent" energy irrelevant to atomic kinds.
In actual atoms, interelectronic Coulomb energy changes "dependent" on other Coulomb terms (= electron-nucleus ) and atomic kinds.
This is the reason why Schrodinger equation is wrong, and cannot solve multi-electron atoms.

2016/8/26 updated. Feel free to link to this site.