---

正弦波をつくる

• 方形波からつくる正弦波
• PWM直交発振器
• PWMからPDMへ

---

経緯

もう今から20年以上前^*1ですが、周期の異なる方形波の排他的論理和(Exclusive-OR)が三角波のPWMになるなら、 バイナリ・カウンタをベースにPWMの正弦波がつくれるのではとの考えに取り憑かれ、試行錯誤の末、基本構成を作り上げました。

今回紹介するのは、またそれから一年以上経ってから CPLD(プログラマブル・ロジック・デバイスの一種)に DAC(オーディオ用ではありません)のテスト用としてインプリメントするため VHDL化したものをベースにしています。

もう永いこと VHDLに係わることもなく ModelSimのような VHDLのコードを検証できる環境もないので、 今後これを紹介することもないだろうと思っていましたが、 最近ディジタル信号処理等の検討に使用し始めた MATLAB互換の数値演算プログラム Octaveで VHDLのロジックをシミュレーションできるのではとふと思いつき、 試してみたところ意外にあっさり VHDLソースから Octaveの .mスクリプトへの移植ができました。

Octaveによるシミュレーション

真ん中のリファレンスのカウンタの方形波(黄緑)と一番上のsinカウンタの波形(赤)との排他的論理和(Exclusive-OR)が、上から二番目のsin PWM波形(マゼンタ)です。 リファレンスのカウンタの方形波(黄緑)と一番下のcosカウンタの波形(青)との排他的論理和が下から二番目のcos PWM波形(シアン)です。これらの正弦波の周期は2048クロックです。

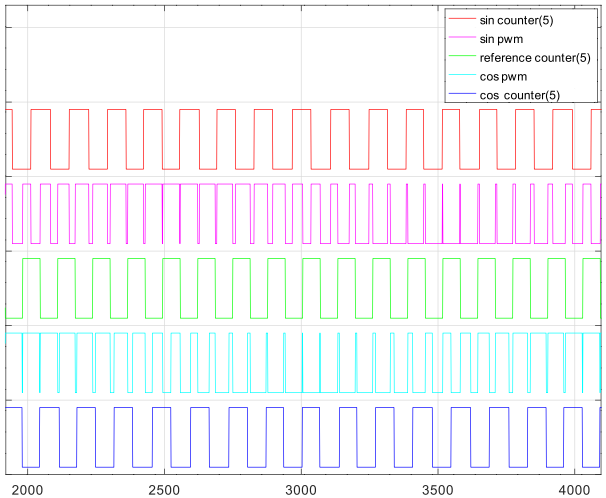
次の図は上の PWMを積分(排他的論理和が真のときは +1, 偽のときは -1を加算)した波形です。比較のために基本波相当の正弦波も表示しています。最初の初期化の 512サイクル以降は安定した正弦波を生成し続けます。

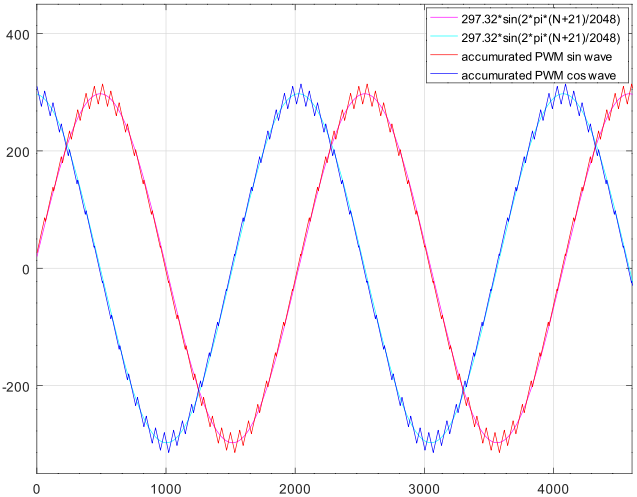
下図は上の積分波形 4周期分を DFT(FFT)した結果です。blackman窓を使用しています。

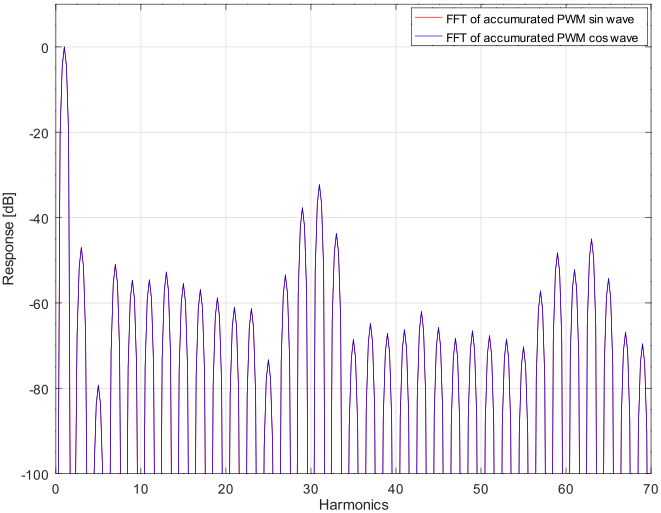
上のスペクトルは方形波同様偶数次の高調波を含んでいません。 31次前後のピークは PWMのキャリア周波数に相当する成分です。 reference, sin, cos の各カウンタは 5ビット (2⁵=32) で構成しています。

動作原理その１. 概要

周期が異なる方形波の排他的論理和(Exclusive-OR)は PWMの三角波になります。
下の回路図は原理説明のための LTspiceの回路図とそのロジックのシミュレーションです。

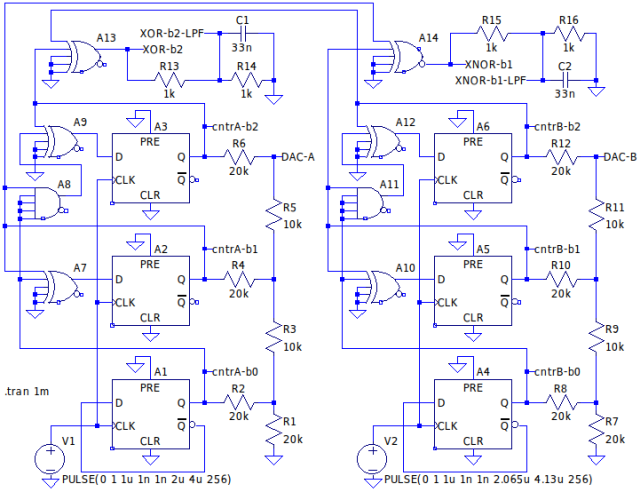
下図最上段の紫色の波形は左右両３ビット・バイナリ・カウンタの MBS(最上位ビット: A2_Q 上から 3段目の青の波形 , A11_Q 上から２段目の黄土色の波形)の Exclusive-OR(A19)と R14,R15,C1によるその積分波形です。
緑の波形は MBS-1ビット(A3_Q 水色の波形 , A12_Q 赤の波形)の Exclusive-NOR(A20)と R13,R16,C2によるその積分波形です。
下から２段目の茶色の階段波形は右の３ビット・バイナリ・カウンタの出力(Q)に接続した R-2R ラダー抵抗ネットワークの出力(R12とR11の交点)です。同様に最下段の青の階段波形は左のバイナリ・カウンタの出力(Q)に接続した R-2Rラダーの出力(R6とR5の交点)になります。

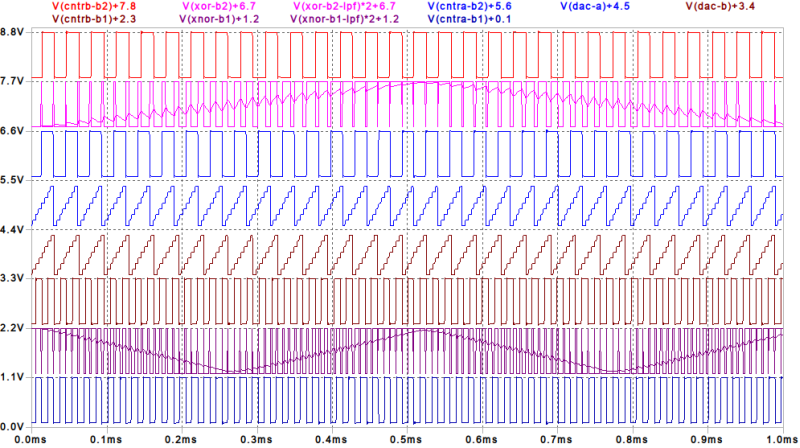
基準となるフリーランのバイナリ・カウンタ(LTspice回路図の左側に相当)とカウント・イネーブルの制御でカウントを間引くことが可能な２個(sin,cos)のバイナリ・カウンタ(LTspice回路図の右側に相当)との排他的論理和(LTspice回路図 A19相当)を PWMの正弦波に近づけるようカウント・イネーブルの制御を工夫しました。

原理的には sinのバイナリ・カウンタの微分で cosのバイナリ・カウンタのカウント・イネーブルの制御を、また cosのバイナリ・カウンタの微分で sinのバイナリ・カウンタのカウント・イネーブルの制御を行えばよいのですが、微分する代わりに基準カウンタと sin, cos のバイナリ・カウンタの 1ビット下(重み1/2)のビットの Exclusive-NOR(排他的論理和の負論理出力)を使用しています。上の LTspiceシミュレーションの緑の波形がそれに相当します。またカウント・イネーブル制御の誤差の蓄積を防ぐため 1/4周期(π/2=90)毎に初期化を行っています。

動作原理その２. 状態方程式

次に、微分の代わりに 1ビット下(重み1/2)の出力の Exclusive-NORが使えることを現代制御理論の状態方程式を用いて説明します(より簡潔明瞭な方法はあるとは思いますが)。下の連立微分方程式が状態方程式です。

$\frac{d}{dt}\mathit{x}=\mathit{A}\mathit{x}+\mathit{B}\mathit{u}$

$\mathit{y}=\mathit{C}\mathit{x}+\mathit{D}\mathit{u}$

大文字は行列、小文字はベクトルを表し、それぞれ

A: システムマトリクス

B: 入力マトリクス

C: 出力マトリクス

D: 伝達マトリクス

x: 状態ベクトル

u: 入力ベクトル

y: 出力ベクトル

と呼ばれますが、多入力多出力の系を扱うため入出力がともにベクトルになっています。『真空管アンプの歪率改善に端を発した古典制御が専ら出力から入力に負帰還をかけることに終始したことに対し、現代制御は出力ではなく系内部の複数の状態変数からの状態フィードバックすることにより多入力多出力の制御が可能になった。』というようなことを40数年前^*2になりますが、制御工学の講義で確か教わった気がします。ちなみに現代制御というのは古典制御との対比から付いた名称のようで、今日では制御理論の中心ではないようです。

前置きはこれまでとし説明に移ります。まず reference 用フリーラン・バイナリ・カウンタに対する cos 用バイナリ・カウンタと sin 用バイナリ・カウンタのカウントの遅延量をそれぞれ x₁ と x₂ します。ロジックとしてはカウント・イネーブルの制御により常に基準カウンタに対して遅れる方向(遅延方向の符号をプラスとすれば単調増加) ですが、排他的論理和を用いての制御は PLLの位相比較器と同様、基準信号との位相関係だけを考えることになります。周回数は無視してトップ争いも周回遅れも同じ扱いです。状態変数 x₁ と x₂ については負の値も認め -1 ≤ x₁, x₂ ≤ 1 とします。

$\frac{d}{dt}\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\mathit{A}\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\mathit{B}\mathit{u}$

$\mathit{y}=\mathit{C}\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\mathit{D}\mathit{u}$

状態方程式も π/2 周期の４つの位相(フェーズ)に分けて考えることにします。 π/2 周期でイニシャライズするため LTspiceのシミュレーション波形を基に位相(フェーズ)と状態変数を以下の表のように定めます。

　

位相(フェーズ)と状態変数

	Phase-1	Phase-2	Phase-3	Phase-4
cosθ	π ≤ θ < 3π/2	3π/2 ≤ θ < 2π	0 ≤ θ < π/2	π/2 ≤ θ < π
sinθ	3π/2 ≤ θ < 2π	0 ≤ θ < π/2	π/2 ≤ θ < π	π ≤ θ < 3π/2
MSB EX-OR duty cycle	0％ → 50％	50％ → 100％	100％ → 50％	50％ → 0％
状態変数 x	-1 → 0	0 → 1	-1 → 0	0 → 1
MSB-1 EX-NOR duty cycle	100％ → 0％	0％ → 100％	100％ → 0％	0％ → 100％

0 ≤ θ < π/2

まず、システムマトリックス

$\mathit{A}=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]$

を考えます。
sin と reference カウンタの MSB-1 ビットの Exclusive-NOR で cos カウンタの制御を
また cos と reference カウンタの MSB-1 ビットの Exclusive-NOR で sin カウンタの制御を行うため、対角要素 a₁₁, a₂₂ は 0 となって

$\frac{d}{dt}{x}_1=a_{12}{x}_2$
$\frac{d}{dt}{x}_2=a_{21}{x}_1$

状態変数 x₁, x₂ は単調増加と規定しましたから a₂₁ x₁, a₁₂ x₂ も正の値で
x₁ < 0 → a₂₁ < 0
x₂ > 0 → a₁₂ > 0
になります。

ここで | a₁₂ | = | a₂₁ | ならば
a₂₁x₁, a₁₂x₂ は【MSB-1 EX-NOR duty cycle】の値に比例します。
| a₁₂ | = | a₂₁ | = ω とするとシステムマトリクス A は

$\mathit{A}=\left[\begin{array}{cc}0& \omega \\ -\omega & 0\end{array}\right]$

になります。

次に状態方程式をラプラス変換して

$\mathrm{s}\mathit{X}\left(\mathrm{s}\right)=\mathit{A}\mathit{X}\left(\mathrm{s}\right)+\mathit{B}\mathit{U}\left(\mathrm{s}\right)$
$\mathit{Y}\left(\mathrm{s}\right)=\mathit{C}\mathit{X}\left(\mathrm{s}\right)+\mathit{D}\mathit{U}\left(\mathrm{s}\right)$

とします。

状態ベクトルの初期値を x₀ とすると

$\mathrm{s}\mathit{X}\left(\mathrm{s}\right)-x_0=\mathit{A}X\left(\mathrm{s}\right)$
$\left(\mathrm{s}\mathbf{I}-\mathit{A}\right)\mathit{X}\left(\mathrm{s}\right)=x_0$
$\mathit{X}\left(\mathrm{s}\right)={\left(\mathrm{s}\mathbf{I}-\mathit{A}\right)}^{-1}{x}_0\left(=\varphi \left(\mathrm{s}\right)x_0\right)$

これをラプラス逆変換し時間関数に戻すと
$x\left(t\right)={\mathcal{L}}^{-1}\mathit{X}\left(\mathrm{s}\right)={\mathcal{L}}^{-1}\varphi \left(\mathrm{s}\right)x_0=\varphi \left(t\right)x_0$

状態ベクトルの初期値 x₀ と状態遷移マトリクス φ(t) から自由応答 x(t) が得られます。
(ただしこの系では入力はないものとして BU(s)=[0] とします。) これで準備が整いました。

まず特性方程式 sI?A は

$\mathrm{s}\mathbf{I}-\mathit{A}=\left[\begin{array}{cc}\mathrm{s}& -\omega \\ \omega & \mathrm{s}\end{array}\right]$

次に sI?A の逆行列 (sI?A)^?1 (= φ(s)) を求めます。

$\varphi \left(\mathrm{s}\right)={\left(\mathrm{s}\mathbf{I}-\mathit{A}\right)}^{-1}=\frac{1}{\left|\mathrm{s}\mathbf{I}-\mathit{A}\right|}\left[\begin{array}{cc}\mathrm{s}& \omega \\ -\omega & \mathrm{s}\end{array}\right]=\frac{1}{{\mathrm{s}}^2+{\omega }^2}\left[\begin{array}{cc}\mathrm{s}& \omega \\ -\omega & \mathrm{s}\end{array}\right]=\left[\begin{array}{cc}\frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}& \frac{\omega }{{\mathrm{s}}^2+{\omega }^2}\\ \frac{-\omega }{{\mathrm{s}}^2+{\omega }^2}& \frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}\end{array}\right]$

【Phase-3】の【状態変数 x 】の初期値 -1 と【Phase-2】の【状態変数 x 】の初期値 0 から

$x_0=\left[\begin{array}{c}-1\\ 0\end{array}\right]$

として、自由応答を求めます。

$\varphi \left(t\right)x_0={\mathcal{L}}^{-1}\left[\begin{array}{cc}\frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}& \frac{\omega }{{\mathrm{s}}^2+{\omega }^2}\\ \frac{-\omega }{{\mathrm{s}}^2+{\omega }^2}& \frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}\end{array}\right]x_0=\left[\begin{array}{cc}\cos \omega t& \sin \omega t\\ -\sin \omega t& \cos \omega t\end{array}\right]\left[\begin{array}{c}-1\\ 0\end{array}\right]=\left[\begin{array}{c}-\cos \omega t\\ \sin \omega t\end{array}\right]$

出力マトリックス

$\mathit{C}=\left[\begin{array}{cc}{c}_{11}& c_{12}\\ c_{21}& c_{22}\end{array}\right]$

の対角要素 C₁₁, C₂₂ の符号は cos と sin それぞれの【MSB EX-OR duty cycle】が単調増加のときプラス、単調減少のときマイナスになります。また対角要素以外は 0 になります。
したがって係数を１とすると出力マトリックスは

$\mathit{C}=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$

バイアス成分を除いた^*1出力は

$\mathit{y}=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}-\cos \omega t\\ \sin \omega t\end{array}\right]=\left[\begin{array}{c}\cos \omega t\\ \sin \omega t\end{array}\right]$

π/2 ≤ θ < π

状態変数の符号から
x₁ ≥ 0 → a₂₁ > 0
x₂ ≥ 0 → a₁₂ > 0

システムマトリックス A は

$\mathit{A}=\left[\begin{array}{cc}0& -\omega \\ \omega & 0\end{array}\right]$

特性方程式 sI?A は

$\mathrm{s}\mathbf{I}-\mathit{A}=\left[\begin{array}{cc}\mathrm{s}& \omega \\ -\omega & \mathrm{s}\end{array}\right]$

次に sI?A の逆行列 (sI?A)^?1 (= φ(s)) を求めます。

$\varphi \left(\mathrm{s}\right)={\left(\mathrm{s}\mathbf{I}-\mathit{A}\right)}^{-1}=\frac{1}{\left|\mathrm{s}\mathbf{I}-\mathit{A}\right|}\left[\begin{array}{cc}\mathrm{s}& -\omega \\ \omega & \mathrm{s}\end{array}\right]=\frac{1}{{\mathrm{s}}^2+{\omega }^2}\left[\begin{array}{cc}\mathrm{s}& -\omega \\ \omega & \mathrm{s}\end{array}\right]=\left[\begin{array}{cc}\frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}& \frac{-\omega }{{\mathrm{s}}^2+{\omega }^2}\\ \frac{\omega }{{\mathrm{s}}^2+{\omega }^2}& \frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}\end{array}\right]$


【Phase-4】の【状態変数 x】の初期値 0 と【Phase-3】の【状態変数 x】の初期値 -1 から

$x_0=\left[\begin{array}{c}0\\ -1\end{array}\right]$

として、自由応答を求めます。

$\varphi \left(t\right)x_0={\mathcal{L}}^{-1}\left[\begin{array}{cc}\frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}& \frac{-\omega }{{\mathrm{s}}^2+{\omega }^2}\\ \frac{\omega }{{\mathrm{s}}^2+{\omega }^2}& \frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}\end{array}\right]x_0=\left[\begin{array}{cc}\cos \omega t& -\sin \omega t\\ \sin \omega t& \cos \omega t\end{array}\right]\left[\begin{array}{c}0\\ -1\end{array}\right]=\left[\begin{array}{c}\sin \omega t\\ -\cos \omega t\end{array}\right]$

【MSB EX-OR duty cycle】の傾きから、出力マトリクスは

$\mathit{C}=\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]$

バイアス成分を除いた^*1出力は

$\mathit{y}=\left[\begin{array}{cc}-1& 0\\ -0& 1\end{array}\right]\left[\begin{array}{c}\sin \omega t\\ -\cos \omega t\end{array}\right]=\left[\begin{array}{c}-\sin \omega t\\ \cos \omega t\end{array}\right]=\left[\begin{array}{c}\cos \left(\omega t+\frac{\pi }{2}\right)\\ \sin \left(\omega t+\frac{\pi }{2}\right)\end{array}\right]$

π ≤ θ < 3π/2

状態変数の符号から
x₁ < 0 → a₂₁ < 0
x₂ > 0 → a₁₂ > 0

システムマトリックス A は

$\mathit{A}=\left[\begin{array}{cc}0& \omega \\ -\omega & 0\end{array}\right]$

特性方程式は 0 ≤ θ < π/2 と同じで

$\varphi \left(\mathrm{s}\right)={\left(\mathrm{s}\mathbf{I}-\mathit{A}\right)}^{-1}=\left[\begin{array}{cc}\frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}& \frac{\omega }{{\mathrm{s}}^2+{\omega }^2}\\ \frac{-\omega }{{\mathrm{s}}^2+{\omega }^2}& \frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}\end{array}\right]$

初期値 x₀ は【Phase-1】の【状態変数 x】の初期値 -1 と【Phase-4】の【状態変数 x】の初期値 0 から

$x_0=\left[\begin{array}{c}-1\\ 0\end{array}\right]$

特性方程式と初期値が 0 ≤ θ < π/2 と同じなので自由応答も同じになります。

$\varphi \left(t\right)x_0=\left[\begin{array}{c}-\cos \omega t\\ \sin \omega t\end{array}\right]$

【MSB EX-OR duty cycle】の傾きから、出力マトリクスは

$\mathit{C}=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$

バイアス成分を除いた^*1出力は

$\mathit{y}=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{c}-\cos \omega t\\ \sin \omega t\end{array}\right]=\left[\begin{array}{c}-\cos \omega t\\ -\sin \omega t\end{array}\right]=\left[\begin{array}{c}\cos \left(\omega t+\pi \right)\\ \sin \left(\omega t+\pi \right)\end{array}\right]$

3π/2 ≤ θ < 2π

状態変数の符号から
x₁ > 0 → a₂₁ > 0
x₂ < 0 → a₁₂ < 0

システムマトリックス A は

$\mathit{A}=\left[\begin{array}{cc}0& -\omega \\ \omega & 0\end{array}\right]$

特性方程式は π/2 ≤ θ < π と同じで

$\varphi \left(\mathrm{s}\right)={\left(\mathrm{s}\mathbf{I}-\mathit{A}\right)}^{-1}=\left[\begin{array}{cc}\frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}& \frac{-\omega }{{\mathrm{s}}^2+{\omega }^2}\\ \frac{\omega }{{\mathrm{s}}^2+{\omega }^2}& \frac{\mathrm{s}}{{\mathrm{s}}^2+{\omega }^2}\end{array}\right]$

初期値 x₀ は【Phase-2】の【状態変数 x】の初期値 0 と【Phase-1】の【状態変数 x】の初期値 -1 から

$x_0=\left[\begin{array}{c}0\\ -1\end{array}\right]$

特性方程式と初期値が π/2 ≤ θ < π と同じなので自由応答も同じになります。

$\varphi \left(t\right)x_0=\left[\begin{array}{c}\sin \omega t\\ -\cos \omega t\end{array}\right]$

【MSB EX-OR duty cycle】の傾きから、出力マトリクスは

$\mathit{C}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$

バイアス成分を除いた^*1出力は

$\mathit{y}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}\sin \omega t\\ -\cos \omega t\end{array}\right]=\left[\begin{array}{c}\sin \omega t\\ -\cos \omega t\end{array}\right]=\left[\begin{array}{c}\cos \left(\omega t+\frac{3\pi }{2}\right)\\ \sin \left(\omega t+\frac{3\pi }{2}\right)\end{array}\right]$

*1:【MSB EX-OR duty cycle】の 50％に相当するバイアス成分を入れるには、伝達マトリクスと入力ベクトルの掛け算 Du の各要素を 0.5 とすればよいのですが、その一方で Bu を[0]とするのは如何にもご都合主義といった感じで気が進みません。というわけでバイアス成分は省かせて頂きました。

動作原理その３. ω=π/2 の近似

1/4周期毎に初期化するので、1/4周期を単位時間(=1)とすると

$\omega =\frac{\pi }{2}=1.5708\hspace{0.25em}\cdots$

この値の近似のため Exclusive-NOR の出力で 9進カウンタをインクリメント(+1)しつつ、カウント・イネーブル制御用の 5ビットカウンタでは 9進カウンタの値が 0,2,4,6 のときは +1 また 1,3,5,7,8 では +3 して

$\frac{\left(4+2\times 5\right)}{9}=1.5555\hspace{0.25em}\cdots$ ^*3

の割合でカウント・アップし cos または sin 用のバイナリ・カウンタのカウント・イネーブルを生成してカウントの間引きを行っています。

下図は具体的なその様子を示した Octave によるシミュレーション波形です。

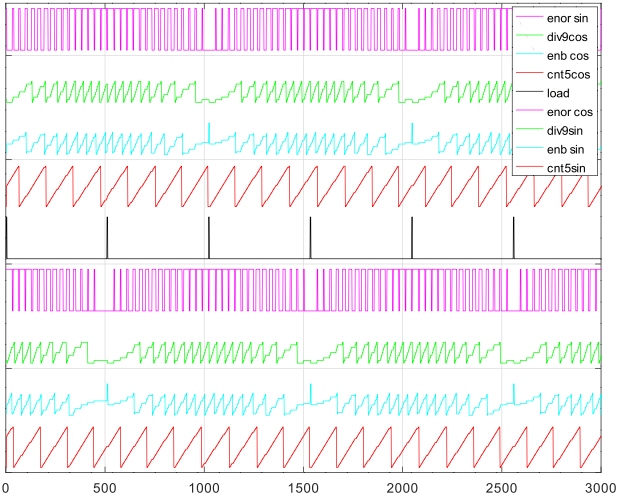
真ん中の黒のパルスは 1/4周期のイニシャライズ用のストローブ信号です。中央から上は cos 用カウンタ(赤)とカウント・イネーブル生成のための信号、中央から下は sin 用カウンタ(赤)とカウント・イネーブル生成のための信号です。

マゼンタの信号は MSB-1ビットの Exclusive-NOR の信号です。この信号が１のとき下の黄緑色の 9ビット・カウンタとシアンのカウント・イネーブル制御用の 5ビットカウンタがカウント・アップします。

間引きの回数は 1/4周期あたり 8クロックの１周期 32(=2⁵)クロックです。これは 5ビットの cos および sin 用のバイナリ・カウンタが reference カウンタに対し、ちょうど１周回遅れすることを意味しています。

• 方形波からつくる正弦波
• (PREV)

• PWM直交発振器

• (NEXT)
• PWMからPDMへ