正弦波をつくる
2値のPWMから3値のPWMへ
下は2値の正弦波PWMを3値のPWM*1化するためのロジックをシミュレーションするためのLTspiceの回路図です。
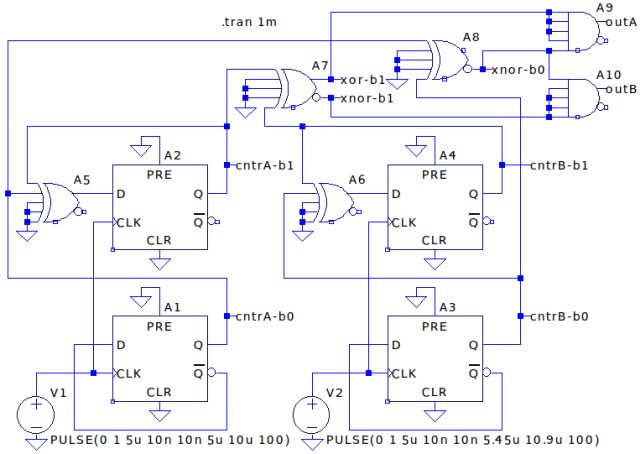
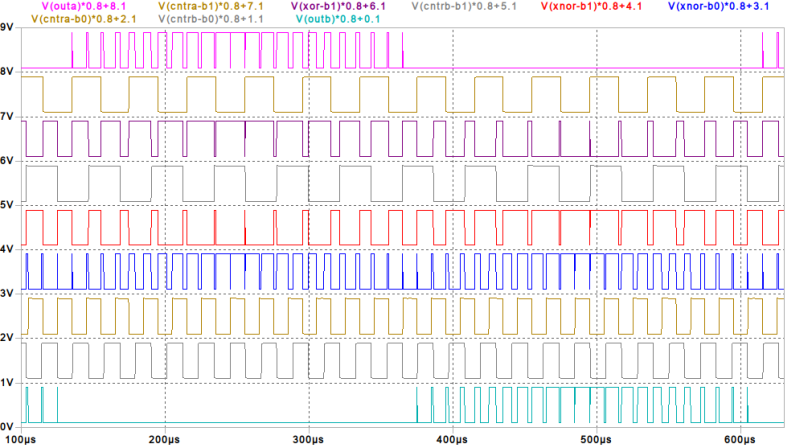
3値のPWM*1化とちょっとした小細工で劇的に特性が改善できました。
具体的には本ロジックのステート・マシーンは4ステートからできており(Octaveの .mファイル参照)、基準カウンタ(cnt9bit)とsin,cos両カウンタ(cnt5sin,cnt5cos)のMSB(24ビット), MSB-1(23ビット)を直接使用せず、それぞれ別の3ビット・バイナリ・カウンタ(cnt5ref,dbl5sin,dbl5cos)にロードし直し、 この3ビット・カウンタのMSBのExclusive-ORとMSB-1のExclusive-NORを利用することに加え、各3ビット・カウンタをロードした2サイクル後に無条件でインクリメントしたことです。
この小細工に関するステートマシーンの各ステートでの処理を以下に示します。
- cnt9bitのインクリメントとcnt5sin,cnt5cos条件付きインクリメント
- cnt5ref,dbl5sin,dbl5cosを無条件でインクリメント
- cnt9bitとcnt5sin,cnt5cosの22~24ビット → cnt5ref,dbl5sin,dbl5cos にロード
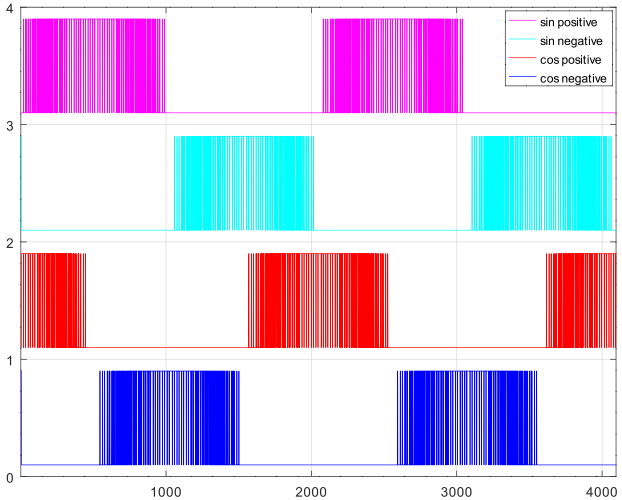
下図は上図をズームしたものです。
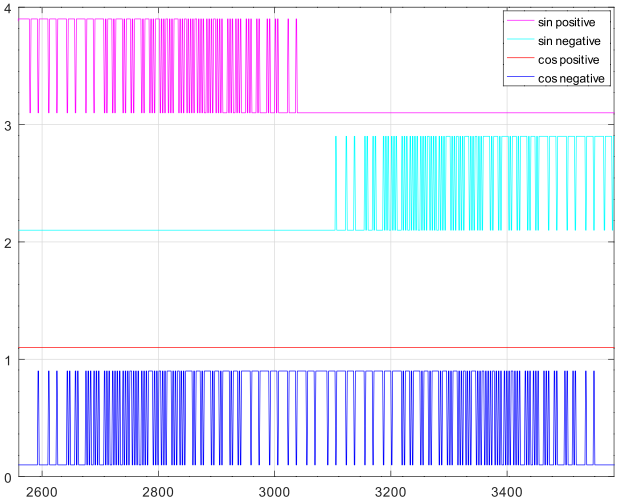
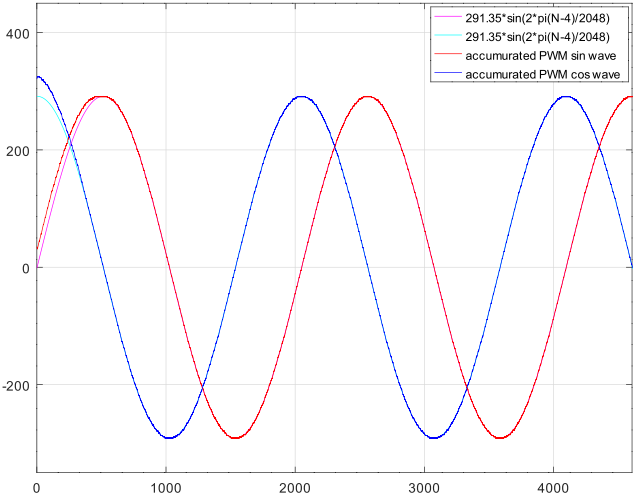
3値のPWM*1の信号を積分したのが下図です。極めて歪みの少ない正弦波になっていることが判ります。
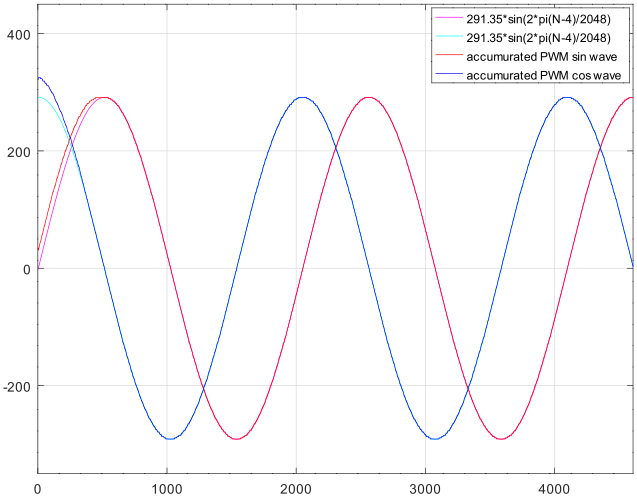
次は上図の PWMを積分した波形 4周期分を FFT(DFT)した結果です。blackman窓を使用しています。各高調波がほぼ -60dBまでに収まりました。振幅の分解能を考えればほぼ究極の値ではないでしょうか。
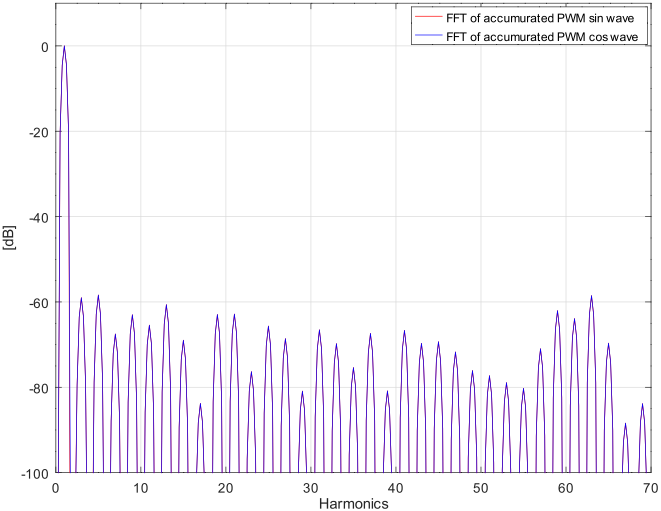
高調波のレベルだけでなく、また sinと cosの各高調波の値が一致していることも判ります。なおデータの範囲を 512(=π/4)ずらして sinと cos を相似な波形にして FFT(DFT)をとると sinと cosの結果は完全に一致(直交)します。
再度シングルエンド化
3値のPWM*1では使い勝手が悪いということもあるかと思います。3値のPWM*1の差動信号をシングル・エンド化するのは実は簡単です。直交発振器のロジック(ステートマシーン)は前述のように4クロック(ステート)単位で動作するように作られていて、例の小細工は2クロック毎にロード/カウントアップを交互に繰り返します。これは出力データが必ず2クロックのペアになることを意味します。3値のPWM*1の出力は3値ですから '11'/'10'or'01'/'00' でよいことになります。
中間値を'01'としたときの積分波形 4周期分の FFT(DFT)です。blackman窓を使用しています。
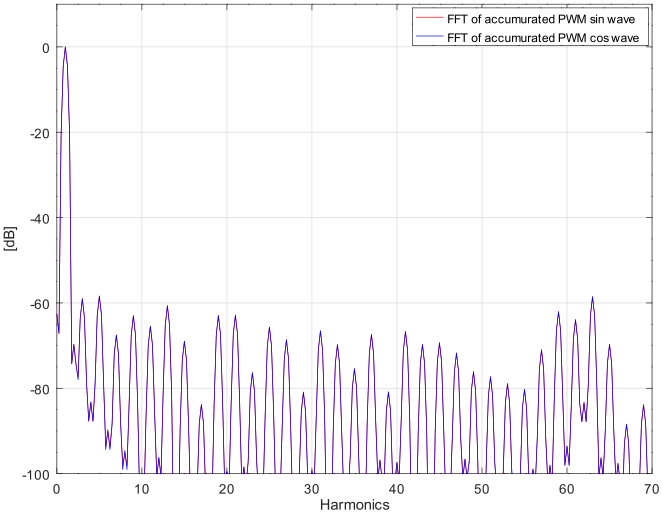
中間値を'10'としたときの積分波形 4周期分の FFT(DFT)です。blackman窓を使用しています。

中間値をトグル(前値の反転)にしたときの積分波形 4周期分の FFT(DFT)です。同じく blackman窓を使用しています。
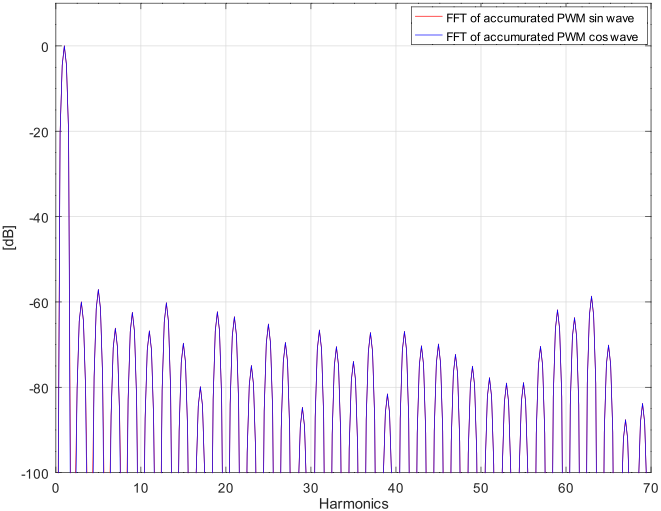
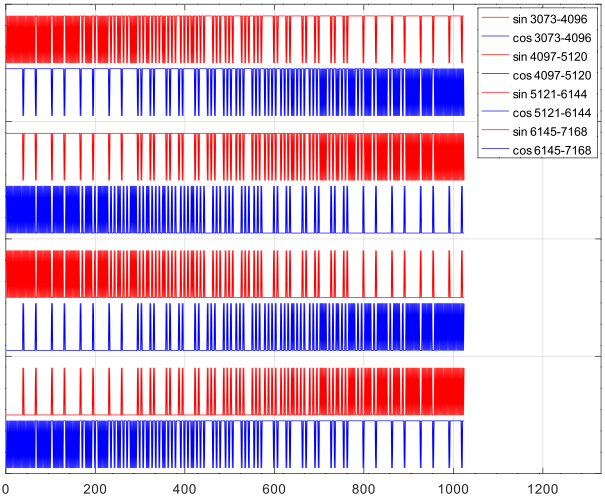
偶数次の高調波が出ないことから、とりあえず中間値はトグル(前値の反転)とします。下図はその FFT(DFT)する前の積分波形です。
下図は再シングルエンド化した PWM波形ですが、むしろ PDM(Pulse-density modulation)波形といった方が良いと思います。なお解像度の都合から 1/4周期毎に分割しています。
高調波のキャンセルによる低歪化
トグルで中間値を生成すると偶数次の高調波が無くなるので、方形波からつくる正弦波/第3高調波の相殺を考えると同じ手法が適応できます。下図は位相が π/4 づつずれた 3波(2波はsinとcosの関係です)を抵抗(51k,36k,51k)でミキシングしたときのシミュレーションの FFT(DFT)です。
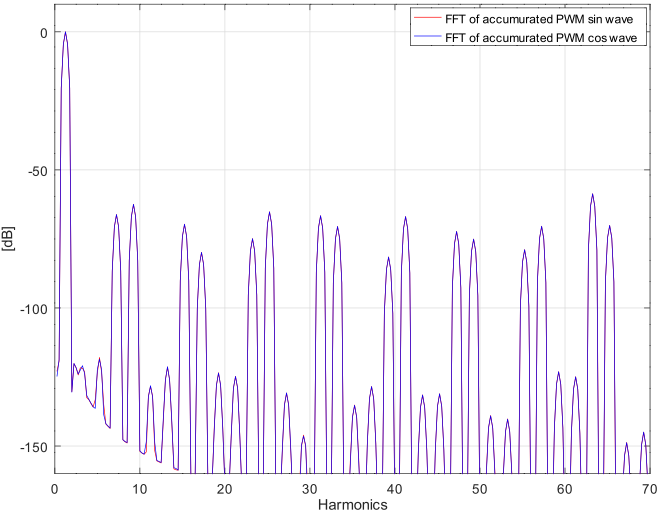
同様に下図は方形波からつくる正弦波/更なる高調波のキャンセルと同じく π/8 づつずれた 7波を抵抗でミキシングしたときのシミュレーションの FFT(DFT)です。
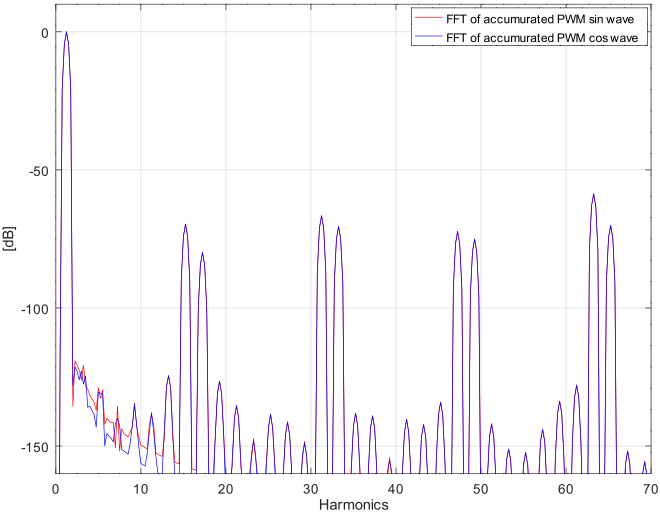
正弦波を重ねてキャンセルする場合に比べて元々の高調波のレベルが低く、1%抵抗の使用で 40dB程度は高調波を低減できるとすると、オーディオ DACを使った DDS(Direct Digital Synthesizer) と遜色のない性能が得られる可能性もあるのではないでしょうか。
7波を生成するのは現実的ではないようにも思えますが、直交発振器のロジックは前述のように4クロック単位で動作するように作られていますから、処理を4段パイプライン化することで多少なりともリソースを抑えて7波(相)化できる気がします。
Octaveの .m ファイル
clear -all
#initial
st = [0,0];
cnt9bit = [0,0,0,0,0,0,0,0,0,0];
cnt5ref = [0,0,0];
dbl5sin = [0,0,0];
dbl5cos = [0,0,0];
cnt5sin = [0,0,0,0,0];
cnt5cos = [0,0,0,0,0];
div9sin = [0,0,0,0];
div9cos = [0,0,0,0];
enb_sin = [0,0,0,0,0];
enb_cos = [0,0,0,0,0];
cnt9lst = [1,1];
enor_sin = 0;
enor_cos = 0;
load = 0;
sin_p = 0;
sin_n = 0;
cos_p = 0;
cos_n = 0;
#NOT
function y = not_(a)
y = 1-a;
end
#OR
function y = or_(a,b)
y = 1-(1-a)*(1-b);
end
#Exclusive OR
function y = xor_(a,b)
y = a*(1-b)+(1-a)*b;
end
#Exclusive NOR
function y = xnor_(a,b)
y = a*b+(1-a)*(1-b);
end
#increment 2-bit binary counter
function y = cntr2inc1(a)
a2 = xor_(a(2),a(1));
a1 = not_(a(1));
y = [a1,a2];
end
#increment 3-bit binary counter
function y = cntr3inc1(a)
a3 = xor_(a(3),a(2)*a(1));
a2 = xor_(a(2),a(1));
a1 = not_(a(1));
y = [a1,a2,a3];
end
#increment 4-bit binary counter
function y = cntr4inc1(a)
a4 = xor_(a(4),a(3)*a(2)*a(1));
a3 = xor_(a(3),a(2)*a(1));
a2 = xor_(a(2),a(1));
a1 = not_(a(1));
y = [a1,a2,a3,a4];
end
#increment 5-bit binary counter
function y = cntr5inc1(a)
a5 = xor_(a(5),a(4)*a(3)*a(2)*a(1));
a4 = xor_(a(4),a(3)*a(2)*a(1));
a3 = xor_(a(3),a(2)*a(1));
a2 = xor_(a(2),a(1));
a1 = not_(a(1));
y = [a1,a2,a3,a4,a5];
end
#increment 9-bit binary counter
function y = cntr9inc1(a)
a9 = xor_(a(9),a(8)*a(7)*a(6)*a(5)*a(4)*a(3)*a(2)*a(1));
a8 = xor_(a(8),a(7)*a(6)*a(5)*a(4)*a(3)*a(2)*a(1));
a7 = xor_(a(7),a(6)*a(5)*a(4)*a(3)*a(2)*a(1));
a6 = xor_(a(6),a(5)*a(4)*a(3)*a(2)*a(1));
a5 = xor_(a(5),a(4)*a(3)*a(2)*a(1));
a4 = xor_(a(4),a(3)*a(2)*a(1));
a3 = xor_(a(3),a(2)*a(1));
a2 = xor_(a(2),a(1));
a1 = not_(a(1));
y = [a1,a2,a3,a4,a5,a6,a7,a8,a9];
end
#increment two 5-bit binary counter
function y = cntr5inc2(a)
a5 = xor_(a(5),a(4)*a(3)*a(2));
a4 = xor_(a(4),a(3)*a(2));
a3 = xor_(a(3),a(2));
a2 = not_(a(2));
a1 = a(1);
y = [a1,a2,a3,a4,a5];
end
#for plot data
integsin(1) = -321;
integcos(1) = 35;
#clock cycle loop
for k=1:512+2048
cos_p = xnor_(cnt5ref(2),dbl5cos(2))*xor_(cnt5ref(3),dbl5cos(3));
cos_n = xnor_(cnt5ref(2),dbl5cos(2))*xnor_(cnt5ref(3),dbl5cos(3));
sin_p = xnor_(cnt5ref(2),dbl5sin(2))*xor_(cnt5ref(3),dbl5sin(3));
sin_n = xnor_(cnt5ref(2),dbl5sin(2))*xnor_(cnt5ref(3),dbl5sin(3));
#clock state-0
if st == [0,0]
enor_sin = xnor_(cnt5ref(2),cnt5sin(4));
enor_cos = xnor_(cnt5ref(2),cnt5cos(4));
cnt9bit = cntr9inc1(cnt9bit);
if load == 1
div9sin = [0,0,0,0];
div9cos = [0,0,0,0];
else
if enor_cos == 1
if div9sin == [0,0,0,1]
enb_sin = cntr5inc2(enb_sin);
div9sin = [0,0,0,0];
else
if div9sin(1) == 1
enb_sin = cntr5inc2(enb_sin);
else
enb_sin = cntr5inc1(enb_sin);
end
div9sin = cntr4inc1(div9sin);
end
end
if enor_sin == 1
if div9cos == [0,0,0,1]
enb_cos = cntr5inc2(enb_cos);
div9cos = [0,0,0,0];
else
if div9cos(1) == 1
enb_cos = cntr5inc2(enb_cos);
else
enb_cos = cntr5inc1(enb_cos);
end
div9cos = cntr4inc1(div9cos);
end
end
end
#clock state-1
elseif st == [1,0]
dbl5cos = cntr3inc1(dbl5cos);
dbl5sin = cntr3inc1(dbl5sin);
cnt5ref = cntr3inc1(cnt5ref);
load = or_(xor_(cnt9bit(8),cnt9lst(1)),xor_(cnt9bit(9),cnt9lst(2)));
#clock state-2
elseif st == [0,1]
if load == 1
cnt5sin = [0,0,0,not_(cnt9bit(8)),not_(cnt9bit(9))];
cnt5cos = [0,0,0,cnt9bit(8),xnor_(cnt9bit(8),cnt9bit(9))];
if enb_sin == [1,0,0,1,0]
enb_sin = [0,0,0,1,1];
elseif enb_sin == [0,1,0,1,0]
enb_sin = [0,0,0,1,1];
elseif enb_sin == [1,1,0,1,0]
enb_sin = [0,0,0,1,1];
elseif enb_sin == [0,0,1,1,0]
enb_sin = [0,0,0,1,1];
elseif enb_sin == [1,0,1,1,0]
enb_sin = [0,0,0,1,1];
elseif enb_sin == [0,1,1,1,0]
enb_sin = [0,0,0,1,1];
elseif enb_sin == [1,1,1,1,0]
enb_sin = [0,0,0,1,1];
else
enb_sin = [0,0,0,1,0];
end
if enb_cos == [1,0,0,1,0]
enb_cos = [0,0,0,1,1];
elseif enb_cos == [0,1,0,1,0]
enb_cos = [0,0,0,1,1];
elseif enb_cos == [1,1,0,1,0]
enb_cos = [0,0,0,1,1];
elseif enb_cos == [0,0,1,1,0]
enb_cos = [0,0,0,1,1];
elseif enb_cos == [1,0,1,1,0]
enb_cos = [0,0,0,1,1];
elseif enb_cos == [0,1,1,1,0]
enb_cos = [0,0,0,1,1];
elseif enb_cos == [1,1,1,1,0]
enb_cos = [0,0,0,1,1];
else
enb_cos = [0,0,0,1,0];
end
else
if enb_sin(5) == 1
enb_sin(5) = 0;
else
cnt5sin = cntr5inc1(cnt5sin);
end
if enb_cos(5) == 1
enb_cos(5) = 0;
else
cnt5cos = cntr5inc1(cnt5cos);
end
end
#clock state-3
elseif st == [1,1];
dbl5cos = [cnt5cos(3),cnt5cos(4),cnt5cos(5)];
dbl5sin = [cnt5sin(3),cnt5sin(4),cnt5sin(5)];
cnt5ref = [cnt9bit(3),cnt9bit(4),cnt9bit(5)];
cnt9lst = [cnt9bit(8),cnt9bit(9)];
end
#clk state
st = cntr2inc1(st);
#BD modulation to single end
if cos_p == 1
pwmcos = 1;
elseif cos_n == 1
pwmcos = 0;
else
pwmcos = not_(pwmcos);
# pwmcos = not_(st(1));
# pwmcos = st(1);
end
if sin_p == 1
pwmsin = 1;
elseif sin_n == 1
pwmsin = 0;
else
pwmsin = not_(pwmsin);
# pwmsin = not_(st(1));
# pwmsin = st(1);
end
#for plot data
integsin(k+1) = integsin(k)+pwmsin*2-1;
integcos(k+1) = integcos(k)+pwmcos*2-1;
end
#for plot reference data
for n=1:512+2048
sinref(n) = sin(-pi/2+(n-4)*2*pi/2048);
cosref(n) = cos(-pi/2+(n-4)*2*pi/2048);
end
#plot command
plot(291.347*sinref,'m;291.347*sin(2*pi*(N-4)/2048);',291.347*cosref,'c;291.347*cos(2*pi*(N-4)/2048);',integsin,'r;integrated sin pwm;',integcos,'b;integrated cos pwm;')
axis([1,512+2048,-330,330])
grid on
- PWM直交発振器
- (PREV)
- PWMからPDMへ