Home page
Quantum mechanical fine structure is wrong
Einstein relativity is false.
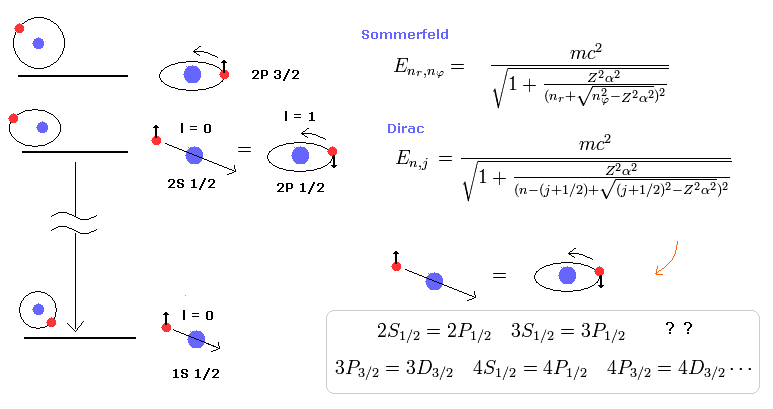
(Fig.1) Quantum mechanical Dirac equation's hydrogen fine structure "accidentally" agreed with Bohr-Sommerfeld's atomic fine structure !? ← Quantum mechanical spin is Not real spin.

Realistic Bohr's atomic model perfectly agreed with all experimental energy levels of all hydrogen-like atoms and ions.
Later, the phony quantum mechanical Schrödinger equation "copied" the Bohr's atomic model and "accidentally" agreed with Bohr's atomic energy levels in an illegitimate way.
As seen in the fact that the successful Bohr model was awarded the most prestigious Nobel prize, the hackneyed phrase "Bohr's model could be unstable radiating energy ?" was a total lie fabricated later to justify the unrealistic quantum mechanics.
In 1916, Sommerfeld extended Bohr's circular orbits to elliptical orbits with various orbital shapes and angular momentums ( this p.4-5 ), and could successfully explain the small energy splitting called fine structure ( this p.2-lower ).
Quantum mechanical Schrödinger equation desperately tried to obtain the same results as the successful Bohr-Sommerfeld's fine structure model which perfectly agreed with experimental results ( this p.5-upper, this p.8-4th-paragraph, this p.5(or p.3)-lower-p.6(or p.4 )-upper ).
Later in 1928, the relativistic quantum mechanical Dirac equation with unreal spin could "accidentally" obtain the same results as the Bohr-Sommerfeld fine structure energy splitting without spin ( this 5th-paragraph, this p.1-left-3rd-paragraph, this p.8-left-lower ).
This p.14-4th and last paragraphs says
"Sommerfeld’s fine-structure formula was spectroscopically confirmed for
H and for hydrogenic ions (He+,
Li2+, ...) to the highest precision—the greatest triumph
of the old quantum theory"
"Over a decade later, after the electron spin had
been discovered, relativistic quantum mechanics
(Dirac 1928) obtained the fine-structure formula (Gordon 1928) along a very
different route....
yields the same energies as Sommerfeld’s formula"
This-3rd-last-paragraph says,
"When Dirac developed relativistic quantum mechanics, the relativistic Coulomb problem proved to be exactly solvable ...But the resulting formula for the energy levels was truly a surprise: The new answer was precisely the old Sommerfeld formula !"
The serious problem is that the relativistic quantum mechanics represented by nonphysical Dirac equation (= which abstract math theory cannot describe atomic phenomena using real visualized objects ) must include unreal electron's spin which spinning speed far exceeds light speed c ( this p.2 ) contradicting Einstein relativity, and this relativistic theory also contains many fatal paradoxes.
It's impossible that Bohr-Sommerfeld model without unreal spin accidentally agreed with the quantum mechanical Dirac's fine structure with unreal spin ( this p.2-3rd-paragraph, this p.1-last~p.2-upper, this p.2-3, this 2nd-paragraph, this last-paragraph ), which fact means the quantum mechanics artificially "copied" the already-existing successful Bohr-Sommerfeld fine structure using artificially-created ad-hoc "spin".
If you compare Bohr-Sommerfeld fine structure energy levels and the quantum mechanical Dirac equation's fine structure ( this p.19, this p.2, this p.3-lower, this p.14-upper ), you will find these two completely-different models "accidentally" gave exactly the same fine structure energies.
As shown in upper figure, quantum mechanical Dirac hydrogen's energy change from spin-down j = 1/2 to spin-up 3/2 corresponds to the change of the orbital (= Not spin ) angular momentum or kinetic energy of ordinary (Schrodinger's and Bohr model's ) hydrogen atomic energy.
It means even quantum mechanical Dirac hydrogen's fine structure does Not use (fictitious) spin nor relativistic spin-orbit interaction.
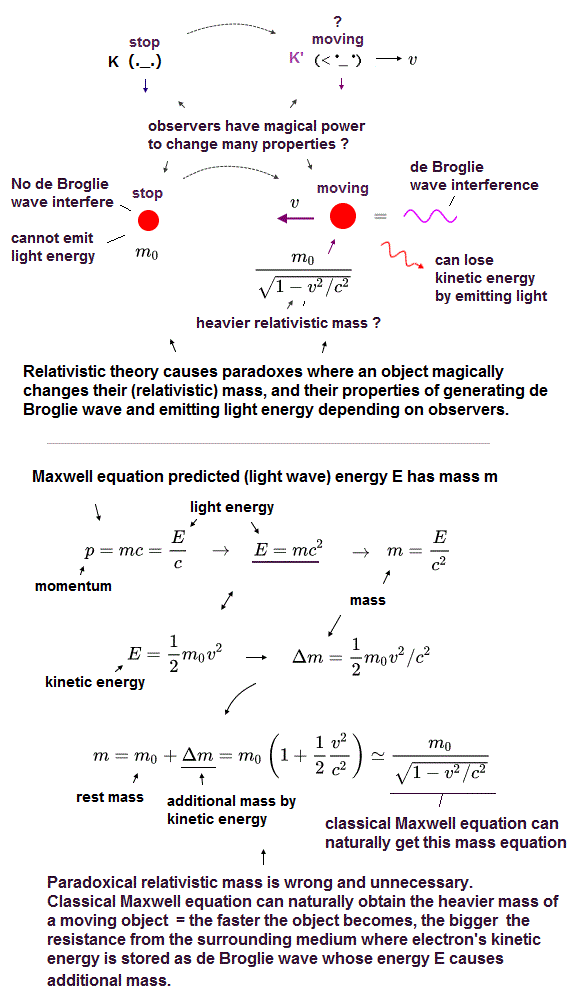
(Fig.2) Einstein relativistic theory causes many paradoxes in mass, kinetic energy, de Broglie wave, emitting light energy, so false.
Einstein relativistic energy and mass are paradoxical and wrong.
In the upper figure, the stationary observer K sees a stationary charged particle with the rest mass m0 and No kinetic energy (= so this stationary particle has No more additional energy to lose by emitting light wave energy ).
But as seen by another observer K' moving at a velocity v, this particle appears to be moving in the opposite direction with heavier relativistic mass and the magically-gained kinetic energy 1/2mv2 which could be lost by emitting light wave energy.
This relativistic theory causes serious paradox where while the moving K' observer sees the moving charged particle emitting light and losing kinetic energy, the stationary K observer sees the stationary charged particle, which magically gains kinetic energy by emitting and losing light energy (= contradiction ! )
Furthermore, the stationary K sees No de Broglie wave in the stationary particle, but the moving K' can magically detect the interference of de Broglie wave of the particle that appears to be moving with kinetic energy and momentum.
↑ Einstein relativistic theory has No absolute frame nor the real medium in space, which relativity causes these fatal irreparable paradoxes ( this p.48-49 ).
It is often said that (realistic) Bohr-Sommerfeld model's successful prediction of the fine structure energy splitting was caused by relativistic effect or relativistic differently-heavier masses between circular and elliptical orbits ( this p.14-upper, this p.8-9 ).
But it is impossible for the paradoxical Einstein relativistic theory to contribute to prediction of actual atomic energy.
In fact, Einstein relativistic energy (= E ) and mass (= m ) relation of E = mc2 was derived by classical Maxwell equation in the 19th century, and Einstein copied this Maxwell authentic mc2 in the wrong way ( this-p.3~ ).
So we can naturally show Bohr-Sommefeld model uses this classical Maxwell's mc2 instead of the paradoxical relativistic mass.
According to Maxwell equation, the energy E causes the additional mass (= Δm = E/c2 ), which means the particle moving with kinetic energy (= 1/2m0v2 ) becomes heavier with the additional mass Δm = kinetic energy/c2, which leads to the ordinary relativistic mass relation as shown in upper figure.
Actually, Bohr-Sommerfeld atomic model (and quantum mechanical Schrodinger hydrogen ) uses only one (absolute) frame (= rest frame of the nucleus ), which means the slightly-heavier mass of a moving electron is due to classical Maxwell's mc2 instead of paradoxical Einstein relativistic mass.
Kinetic energy stored in electron's de Broglie wave (= like the light wave's de Broglie wave ) as the additional mass (= Δm = E/c2 ) in the medium can avoid the ridiculous relativistic mass which could be heavier just by observers' motion without adding any mass.
Actually the so-called (paradoxical) relativistic energy as shown in nuclear mass defect is just the potential energy that needs the realistic medium contradicting Einstein relativity.
As the particle moves faster, it feels more resistance from the surrounding medium where the light speed c is the maximum transmitting speed (= the maximum speed of electric field accelerating charged particle is also light speed c ), hence, this larger resistance is manifest as heavier mass which appears to increase to infinity to prevent the particle's speed from exceeding the maximum speed c in the medium.
(Fig.2') A stationary electron and a proton are separated with No kinetic energy gain kinetic energy and emit light wave energy to form a hydrogen atom, which needs the medium (= potential energy ) as the source of light wave and kinetic energy.
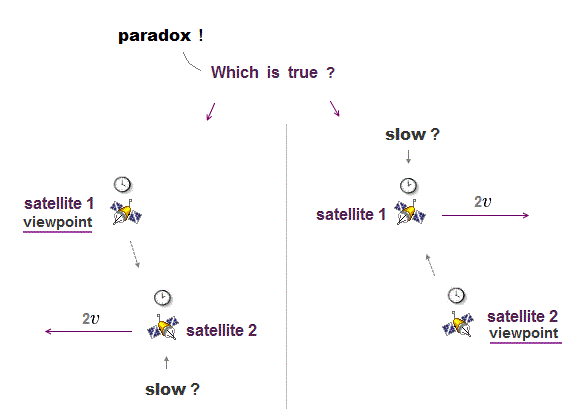
When a stationary electron and a proton separated by a large distance (= Coulomb potential energy between them is almost zero ) attract each other, gain kinetic energy (= increase fake relativistic energy and mass ) to form a hydrogen atom with Coulomb attraction, they emit and lose light wave energy.
↑ Einstein relativity illogically rejecting real medium in space cannot explain this atomic energy level transition (from the excited state to the lowest-energy ground state ) and emission of light wave.
Because both the electron and proton in the bound state in a hydrogen atom gain kinetic energy instead of emitting or losing light wave energy as shown in Fig.2' ← It means the emitted light wave energy in the atomic energy transition from the excited to ground state comes Not from the electron or proton but from the medium around them.
The source of this kinetic energy given to the electron (and the proton ) and the emitted light energy comes from the Coulomb potential energy (= medium ) around these particles.
↑ If the space contains nothing as Einstein relativity claims, there is No source of this emitted light wave energy and the kinetic energy gained by the electron and the proton which attract each other, accelerate and form a hydrogen atom.
As a result, Einstein relativity unreasonably rejecting the medium is wrong, and Not used in the realistic Bohr-Sommerfeld model that uses the authentic Maxwell's energy mc2 stored in the medium as the potential energy.
↑ As shown in Virial theorem, the kinetic energy of the electron (and the proton ) increases when the total potential energy (and the total energy ) decreases (= paradoxically emitting light wave energy ) in the atomic state transition from the excited state to the ground-state in an atom.
(Fig.3) In relativistic theory with No absolute frame nor the medium, the moving observer K' can Not see the ordinary stable circular orbit with fixed angular momentum and quantized de Broglie wavelength.
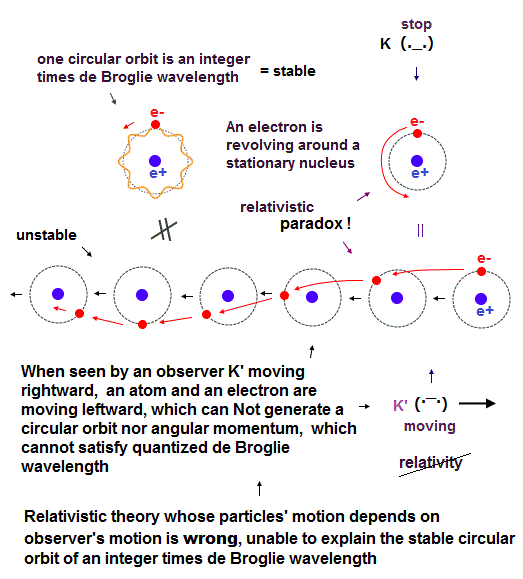
In fact, both (realistic) Bohr-Sommerfeld model and quantum mechanical Schrodinger (hydrogen) atom with fixed orbital angular momentums are incompatible with Einstein relativistic theory.
Because in the upper figure, the stationary K sees the stationary hydrogen atom where an electron is orbiting around the stationary nucleus with fixed angular momentum in the circular orbit with an integer times de Broglie wavelength ( this lower ).
But Einstein relativistic theory has No absolute frame nor the real medium, which is contrary to Bohr-Sommerfeld model and Schrodinger's hydrogen atom.
So the moving observer K' sees the electron is moving in a weird sinusoidal way instead of the regular circular orbit with fixed angular momentum and quantized de Broglie wavelength (= different from Bohr-Sommerfeld model ).
↑ As a result, if Einstein relativistic theory was right, neither Bohr-Sommerfeld model nor quantum mechanical Schrodinger equation's atoms can have the regular circular obits with fixed angular momentum.
So Einstein relativity and its relativistic mass are completely paradoxical and false.
Bohr-Sommerfeld model uses classical Maxwell's authentic mc2 in one absolute frame (= rest frame of nucleus ).
In actual atoms or Bohr-Sommerfeld model, the electron is moving around the (almost-)stationary nucleus in the rest frame of nucleus or the medium, causing the experimentally-verified de Broglie wave avoiding relativistic kinetic energy (= relativistic mass ) paradox.
When the whole atom is moving relative to the medium, it generates new de Broglie wave of the entire atom (or molecule ) inside which an electron is moving around the nucleus ( dragged by the entire atomic de Broglie wave ) in the same way as the nuclear frame generating electron's quantized de Broglie wave.
Bohr-Sommerfeld fine structure model in 1916
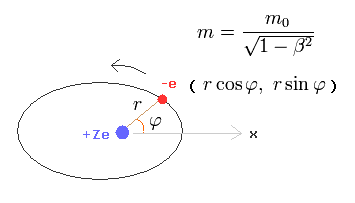
In this section, we calculate the hydrogen atomic fine structure energy splitting using the original realistic Bohr-Sommerfeld model, which results "accidentally" agreed with the later ad-hoc quantum mechanical Dirac's fine structure ( this last, this p.12-14 ).
The important point is that the original "relativistic" Bohr-Sommerfeld atomic model did Not use Einstein's paradoxical relativity or unreal spin, instead, Bohr-Sommerfeld model used the classical Maxwell's energy-momentum relation of mc2.
The following explanation is from the Sommerfeld's original paper ( Annalen der Physik [4] 51, 1-167, 1916, this p.23-28 ).
The simpler Bohr-Sommerfeld elliptical orbits with no fine structure version is calculated on this page.
In the hydrogen-like atom based on the central force, the angular momentum must be always constant and conserved.
↑ This inviolable basic principle of conservation of energy and angular momentum is violated in Einstein relativity where angular momentum is unrealistically changed seen by different observers, hence, relativistic quantum mechanics cannot define the real atomic energies and angular momentums ( this 2nd-paragraph ), and Bohr-Sommerfeld models and relativistic quantum mechanical Dirac equation (= which should conserve angular momentum and energy ) contradict Einstein relativity which is wrong.
In Bohr-Sommerfeld elliptical orbit, the conserved angular momentum ( = p )
is defined as,
(Eq.1)
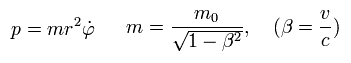
where m0 is the rest mass of an electron, and m is the heavier mass due to kinetic energy that can be explained by Maxwell's mc2 instead of paradoxical relativistic theory.
Change the rectangular coordinates of an electron into the polar coordinates as follows,
(Eq.2)
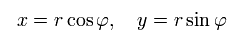
When the nucleus is at the origin (= so Bohr-Sommerfeld uses only the rest frame of a nucleus as the absolute frame contradicting relativistic theory ), the equation of the electron's motion is, (Coulomb force condition)
(Eq.3)
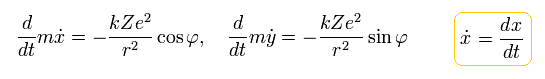
where Z is the atomic number. "-e" and "Ze" are the electric charges of an electron and a nucleus, respectively.
Here we define as follows,
(Eq.4)
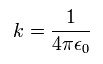
The coordinate r is a function of φ, so we can express the differentiation with respect to t (=time) as follows, (using Eq.1)
(Eq.5)
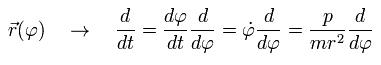
Here we define as follows,
(Eq.6)
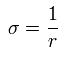
Using Eq.2 and Eq.5, each momentum can be expressed by,
(Eq.7)
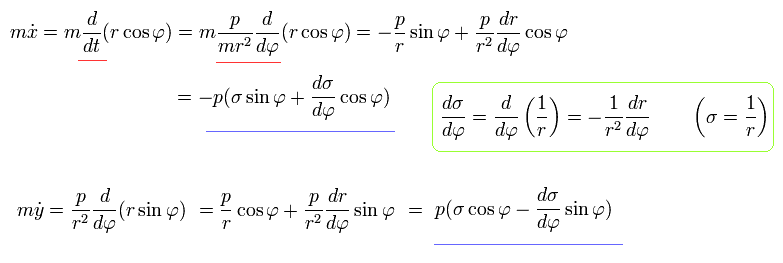
Using Eq.3, Eq.5, and Eq.7, the equation of motion becomes,
(Eq.8)
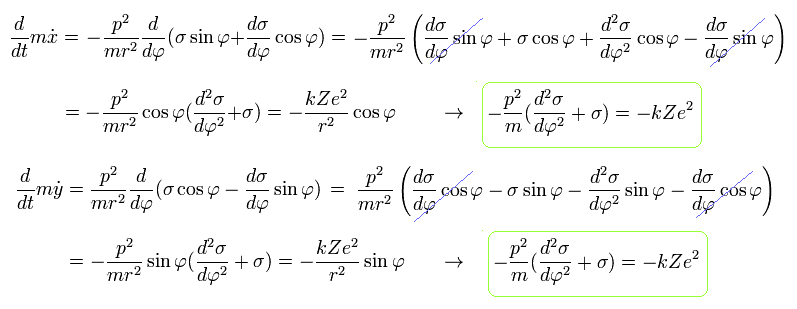
From Eq.8 we obtain the same result of
(Eq.10)
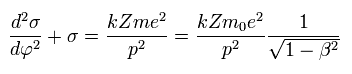
This β is changing with time, so we need to replace this β by other things.
In the hydrogen-like atoms, the total energy W (= T is normal kinetic energy = fictitious relativistic energy (E) - m0c2, V is Coulomb energy in the rest frame of nucleus ) of the Bohr Sommerfeld model is,
(Eq.11)
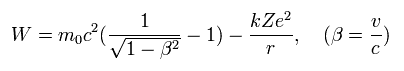
where W is the constant conserved total energy value, which means the sum of the ordinary kinetic (= T ) and Coulomb potential (= V ) energy.
As shown in this, the total energy W of Eq.11 is almost the same as the sum of the ordianry electron's kinetic energy and Coulomb potential energy (= Einstein relativistic dubious huge rest mass energy of an electron or m0c2 is Not used in Bohr-Sommerfeld model ).
From Eq.11, the following equation is obtained using the replacement of Eq.6.
(Eq.12)
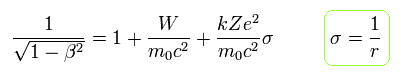
From Eq.10 and Eq.12,
(Eq.13)
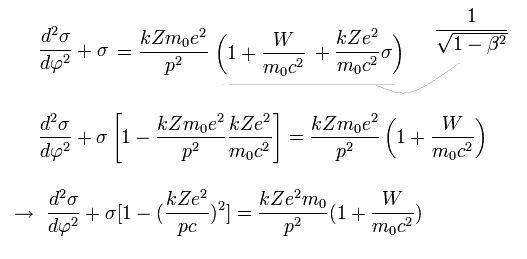
The solution σ of Eq.13 becomes,
(Eq.14)
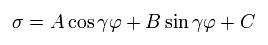
Substituting Eq.14 into Eq.13, γ and C are,
(Eq.15)
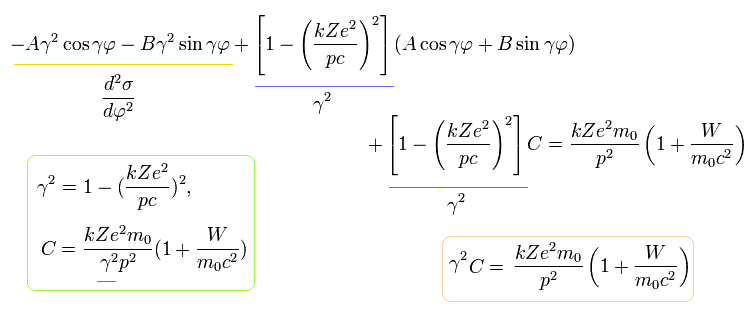
Eq.14 means that the r (= 1 / σ) returns to its original value, when the electron moves the angle of 2π /γ (not 2π).
So the orbit of Bohr-Sommerfeld hydrogen is slightly "precessing" due to the heavier electron's mass influenced by kinetic energy.
For example, after one rotation, the perihelion of the orbit moves the angle of
(Eq.16)
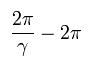
We suppose the first position of the perihelion is at φ = 0.
So the B of Eq.14 becomes zero, as follows,
(Eq.17)
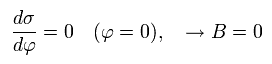
From Eq.6, Eq.14 and Eq.17, we find this electron's orbit is similar to the earth orbiting around the Sun obeying Kepler's law ( this p.1-(2) ) where the central Sun (= nucleus ) stays at the focus of the elliptical orbit.
(Fig.4) "Elliptical" orbit of hydrogen-like atom.
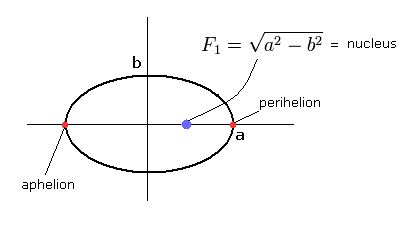
Here, the nucleus is at the focus (F1), and eccentricity (=ε) is,
(Eq.18)
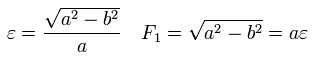
From Eq.14 ( B=0 ), Eq.18, and the condition of the perihelion and aphelion of Fig.4,
(Eq.19)
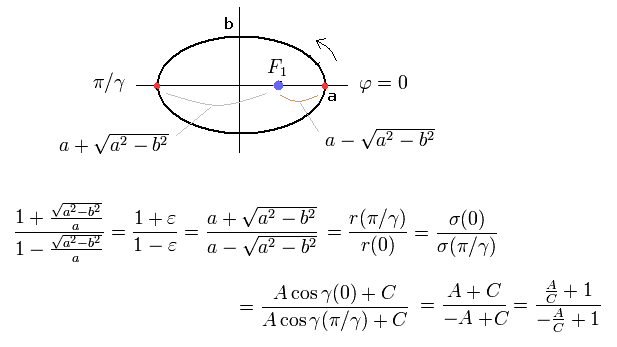
From Eq.19 and Eq.17, A and B of σ in Eq.14 become,
(Eq.20)
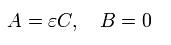
So the r and σ are expressed as,
(Eq.21)
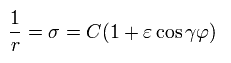
From here, we deal with the hydrogen atom ( Z=1 ).
We define as follows, (substituting Z=1 into Eq.15),
(Eq.22)
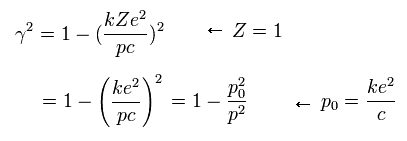
If the angular momentum (p) of the electron is p0, γ becomes zero according to Eq.22.
This means that the precession speed of Eq.16 becomes infinite, when p = p0.
So this p0 is the lower limit of the angular momentum of the Bohr-Sommerfeld hydrogen.
(Of course, in this case the "elliptical" orbit is broken.)
The ratio of p0 to ħ ( = p0/ħ ) is the "famous" fine structure constant (α).
(Eq.23)
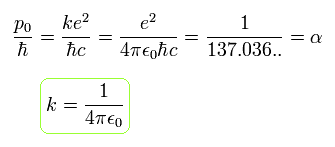
where ħ = h/2π ( h is Planck constant ) is the minimum "quantized" angular momentum of Bohr model.
This means that the fine structure constant α (=1/137) is related to the precession speed of the electron's orbital motion in the Bohr-Sommerfeld model due to the slightly-modified electron mass.
----------------------------------
We can get this fine structure constant α (=1/137) by another simple method ( see also this page. )
By solving the equations of the usual Bohr model hydrogen, the electron's velocity of n=1 orbit becomes
( Electron's velocity in Bohr model hydrogen (n=1). )
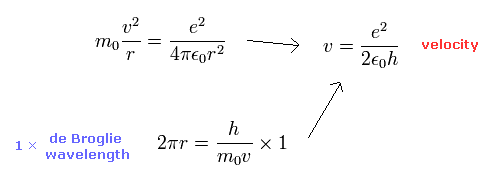
The ratio of this velocity (v) to the speed of light (c) is the fine structure constant α, as follows.
( Fine structure constant )
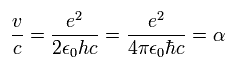
----------------------------------
From Eq.21, when φ is zero, σ, v, and β become,
(Eq.24)
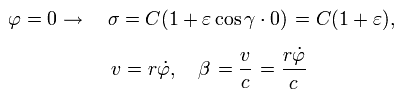
at perihelion, the velocity is perpendicular to the axis.
So when φ =0, the following equation is obtained using Eq.1, Eq.24 and Eq.15 (Z=1),
(Eq.25)
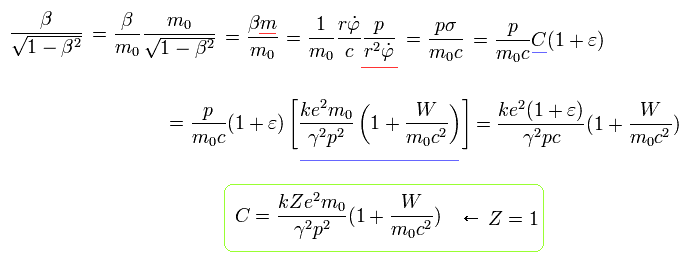
Similarly, from Eq.12, Eq.24 and Eq.15 (Z=1), we can get the equation of
(Eq.26)
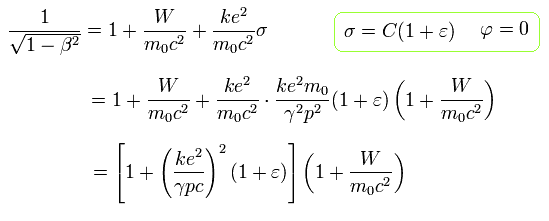
From Eq.22, we obtain the relations of
(Eq.27)
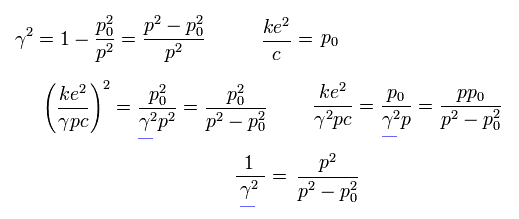
Using Eq.25, Eq.26 and Eq.27, we delete β as follows,
(Eq.28)
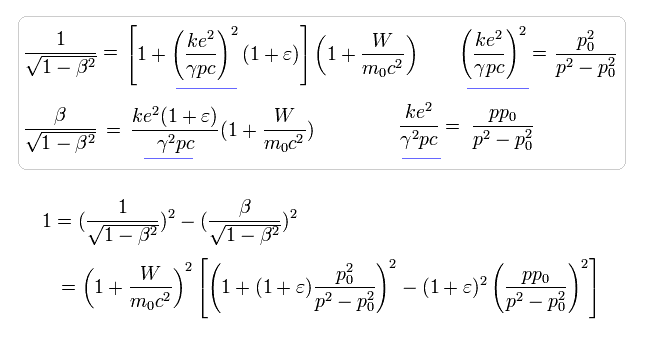
Eq.28 is equal to
(Eq.29)
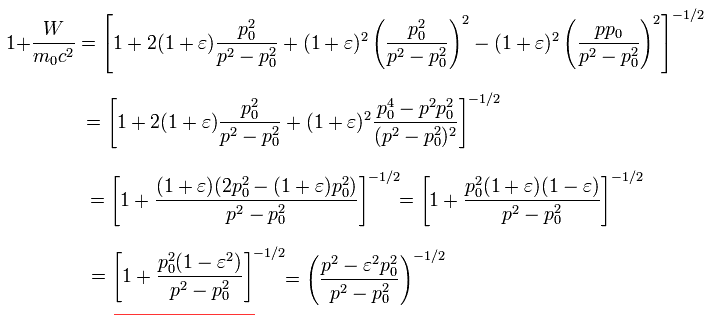
In the Bohr-Sommerfeld quantization condition, the following relations are used ( this p.12 ),
(Eq.32)
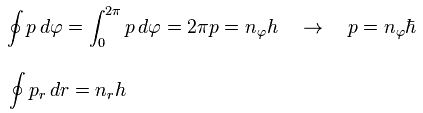
where the angular momentum p is constant.
So p (= orbital angular momentum ) becomes an integer times ħ (= h/2π )
Using Eq.1, the "radial" momentum pr can be expressed as
(Eq.33)
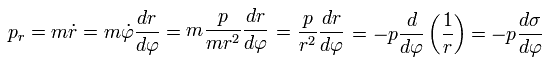
We integrate pr of Eq.32 using Eq.33 and Eq.21 as follows,
(Eq.34)
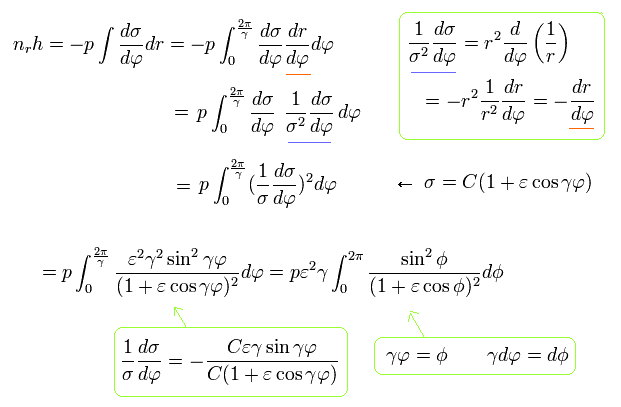
where the original integration interval is from 0 to 2π/γ due to the precession.
And the last term of Eq.34 uses the next replacement,
(Eq.35)
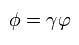
Here as shown in Eq.39 - Eq.48 of this page, we do the partial integration and use the following complex integration formula,
(Eq.39')
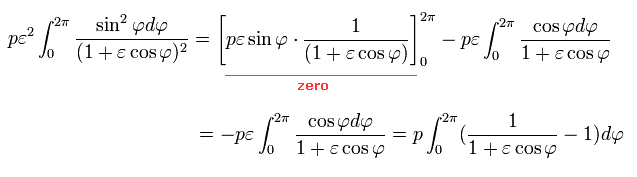
Here we use the following known formula (complex integral, this p.4-5, this p.2, this p.1-2, this p.24-25 ),
(Eq.40')
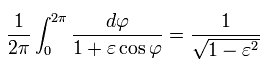
Using Eq.39', Eq.40' and γ of Eq.22, the result of Eq.34 is,
(Eq.36)
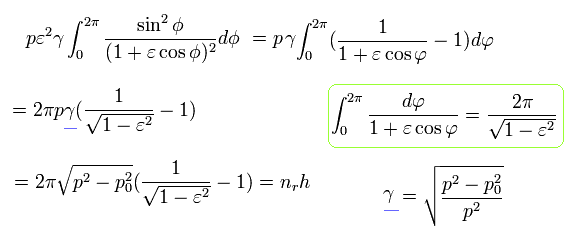
Using Eq.32 and Eq.22,
(Eq.37)
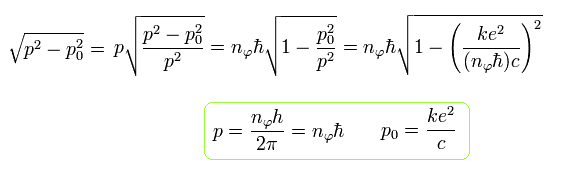
Eq.36 changes to the following equation using Eq.37
(Eq.38)
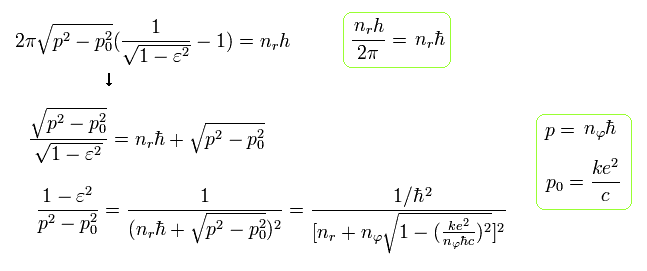
Substituting Eq.38 into the term ( red line ) of Eq.29, and using the fine structure constant α of Eq.23,
(Eq.39)
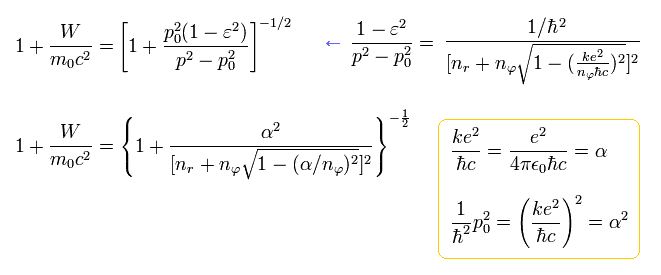
From Eq.39, the energy ( E = W + m0c2 ) becomes, (adding the charge Z)
(Eq.40) ↓ Bohr-Sommerfeld fine structure without spin in 1916

Bohr-Sommerfeld solution of Eq.40 is the same as the Eq.41 solution of Dirac equation.
About the detailed calculation method of Dirac's hydrogen, see this page.
(Eq.41) ↓ Relativistic quantum mechanical Dirac fine structure with spin in 1928
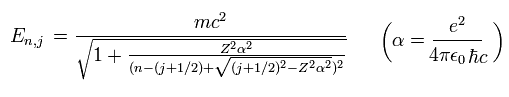
Compare the authentic Bohr-Sommerfeld fine structure in 1916 (= Eq.40, this p.3-last, this p.5, this p.14-upper, this last ) energy splitting and the phony relativistic quantum mechanical Dirac fine structure (= Eq.41, this p.2 ) which "copied" and "accidentally" obtained the same result as the original Bohr-Sommerfeld fine structure by manipulating unreal spin.
This means that the energy levels of Eq.41 are just equal to those of Eq.40, as follows,
2p1/2 (n=2, j=1/2) -------- 2s (nr=1, nφ=1)
2p3/2 (n=2, j=3/2) -------- 2p (nr=0, nφ=2)
This is a very surprising coincidence !
This "artificial conincidence" shows quantum mechanical Dirac hydrogen's spin or spin-orbit fine structure is fake.
When the total angular momentum number j (= spin s + orbital L angular momentums ) is changed from j = 1/2 (= spin-down ) to j = 3/2 (= spin-up ), it has as large influence on total energy n as orbital angular momentum's change ( nϕ ) by 1, which means this spin is fake spin representing orbital angular momentum's kinetic energy, which is why Dirac fine structure with (fake) spin agreed with Bohr-Sommerfel's fine structure without spin.
(Eq.42) Fine structure energy splitting formula

From the fine structure energy levels of Bohr-Sommerfeld hydrogen, we obtain the fine structure energy difference (= energy splitting proportional to Z4/n3 where Z is nuclear charge, n is the principal quantum number, this p.2-(4), this p.14 ) between the orbital angular momentums of nφ and nφ+1 in the same principal quantum number = n = nr (= radial ) + nφ (= angular ).
Realistic Bohr-Sommerfeld hydrogen's fine structure without spin "accidentally agreed" with the later Dirac hydrogen's fine structure with (pseudo-)spin-orbit interaction ( this p.14, this p.12, this p.19 ).
So the upper fine structure formula becomes exactly the same in Bohr-Sommerfeld and relativistic Dirac hydrogen.
In Dirac hydrogen, when the total angular momentum j = 1/2 (= ex. 2p1/2 state with n = 2 ), this corresponds to the Bohr-Sommerfeld hydrogen's orbital angular momentum nφ = 1.
Fine structure energy splitting in Dirac hydrogen's 2p1/2 and 2p3/2 is equal to Bohr-Sommerfeld hydrogen's energy splitting between the orbital angular quantum number = nφ = 1 and nφ = 2 in the same principal quantum number n = 2.
Fine structure energy splitting in Dirac hydrogen's 3p3/2 (or 3d3/2 ) and 3d5/2 is equal to Bohr-Sommerfeld hydrogen's energy splitting between the orbital angular quantum number = nφ = 2 and nφ = 3 in the same principal quantum number n = 3.
(Eq.43) hydrogen's fine structure energy level.
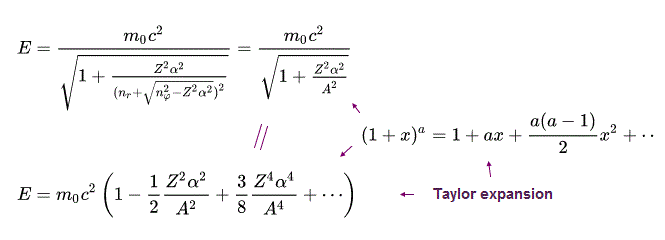
From the energy level of Bohr-Sommerfeld hydrogen's fine structure (= or Dirac hydrogen ), we obtain the upper Eq.43 using Taylor expansion ( this p.2 ) and the following equations.
(Eq.44) Taylor expansion
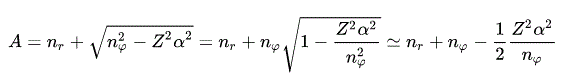
where α is the fine structure constant (= about 1/137 ), which is a small number, so terms of higher-order fine structure constant (= α4 .. ) can be neglected.
(Eq.45)
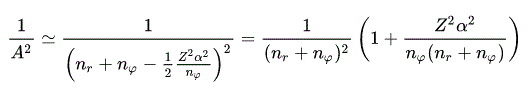
(Eq.46)
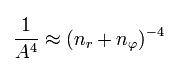
Using Eq.45 and Eq,46, the energy Eq.43 becomes
(Eq.47)
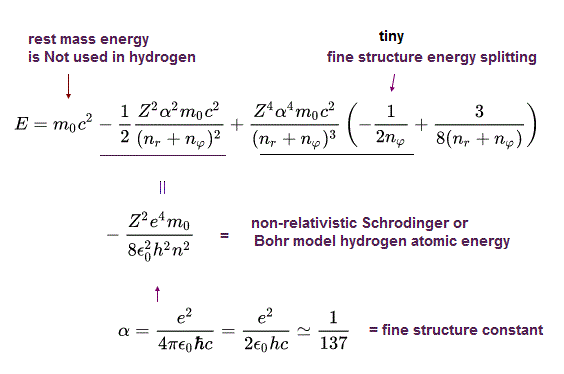
The 2nd term of the upper Eq.47 equals the ordinary non-relativistic Schrodinger's or Bohr model's hydrogen energy levels.
The 3rd term of Eq.47 proportional to α4 gives the small fine structure energy splitting between different angular momentums nφ.
The 4th term of Eq.47 includes only the principal quantum number n = nr + nφ which doesn't contribute to the fine structure energy splitting.
(Eq.48) Fine structure energy splitting formula.

From Eq.47, we obtain the fine structure energy splitting (= difference ) between the orbital angular quantum number nφ and nφ + 1 in the common principal quantum number n as shown in the upper Eq.48.
-----------------------------------------------------------------------------
Here we derive the kinetic energy (= Eq.11 ) from the modified (pseudo-)relativistic mass (= Eq.1, which is actually classical Maxwell's version of mc2 instead of paradoxical Einstein mc2 ) and momentum
We can use the equation of Fig.2 as the particle's momentum.
In this case, the energy (= dT ) required to accelerate the particle during infinitesimal time dt is
(Eq.49)
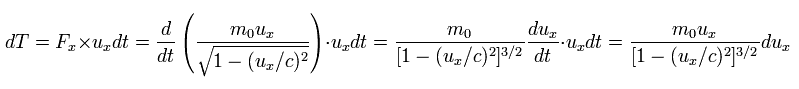
where ux is the velocity in the x direction, and Fx is the force.
where we use
(Eq.50)

So the total kinetic energy required to accelerate the particle to the velocity v is
(Eq.51)
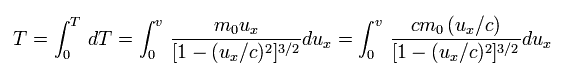
Here we use the replacement of
(Eq.52)
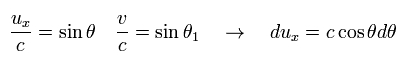
Eq.51 is
(Eq.53)
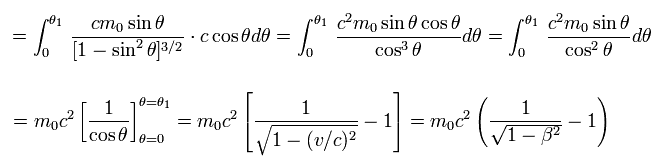
This kinetic energy is completely equal to the first term of Eq.11.
Kinetic energy relation in Bohr-Sommerfeld model is almost the same as the classical kinetic energy.
So the fine structure small energy difference is caused by the small Coulomb potential energy difference caused by the slightly-changed orbital shape by the modified (= slightly-heavier ) mass of an electron affecting the electron's momentum and de Broglie wavelength.
(Eq.54) slightly-modified de Broglie wavelength
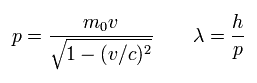
where λ is de Broglie wavelength.
Einstein relativity rejecting the real space medium (= or aether ) causes the serious paradox in de Broglie wave theory (= Einstein relativity is false ), so the relativistic theory cannot use the experimentally-confirmed de Broglie wave relation.
As shown in Eq.49, and Eq.50, when the electric field accelerates an electron in the moving direction (= ux ), the following force Fx is needed.
(Eq.55) slightly-modified momentum
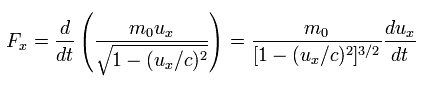
When the electric field accelerates this electron ( uy = 0 ) in the y direction, it needs the force Fy of
(Eq.56)
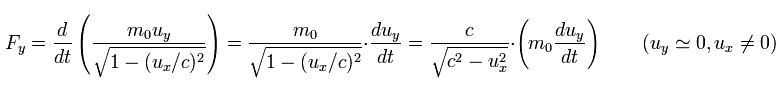
As shown in Eq.55 and Eq.56, the electric field needs more power to accelerate the electron in the moving direction (= x ) than in the y direction.
Because the field in the x direction is "condensed" due to the velocity ux, which causes more resistance.
( In this case, the velocity uy is zero, so the field in the y direction is not condensed. )
So in the case of Eq.56, it is easier to imagine the situation, because the field is not condensed in the acceleration direction.
(Fig.4) Electron is moving in x direction. We accelerate it in y direction.
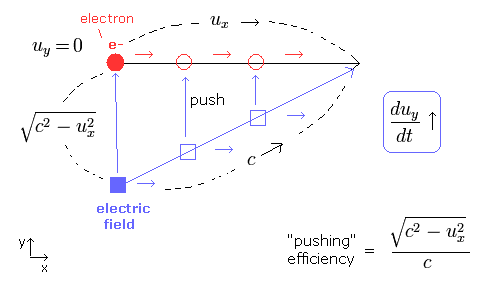
In Fig.4, the electric field is trying to accelerate the electron in the y direction.
To do this, the electric field is moving in the x direction at the same speed (= ux ) as the electron, and pushing the electron in the y direction.
The electric field speed is c, so the "pushing" efficiency becomes as shown in Fig.4.
( When the electron's velocity ux= 0, this pushing efficiency becomes c/c = "1". )
As a result, we can explain the heavier electron mass in Eq.56.
Generalizing this effect, we get the momentum of Eq.54.
The important point is that Bohr Sommerfeld model uses the first order energy term, and consider W = kinetic energy + potential energy of Eq.11 as a "constant". ( See also Eq.25. )
In fact, the second order energy equation of the special relativity can NOT do the addition or subtraction of each particle's energy and momentum normally.
So they needed to introduce a very strange concept of "virtual" particles in the relativistic theory.
-------------------------------------------------------------------------------
According to the Sommerfeld's theory, the energy difference (energy level = n) between k and (k-1) sublevels becomes Eq.59
(See also " The Story of Spin " by Tomonaga.)
(Eq.59)
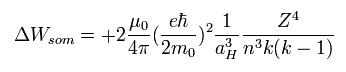
When we want to know the difference between 2s and 2p, we substitute n=2 and k=2 into Eq.59.
(2s --- n=2, (k-1)=1, 2p --- n=2, k=2)
And aH is the Bohr radius and μ0 is the permeability of vacuum.
So they satisfy the following equations.
(Eq.60)
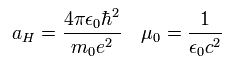
Eq.59 is known to coincide with the experimental values of various atoms such as H, He+, Li++, Be+++.
We calculate Eq.59 ( Z=1, n=2, k=2 ), as follows,
(Eq.61)
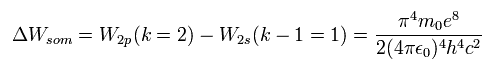
Eq.61 is just equal to Eq.58.
This means that the meaning of Eq.59 is the same as that of Eq.56.
As shown on this page, by equating the angular momentum of the spinning sphere of the electron to 1/2 ħ, the sphere speed leads to more than one hundred times the speed of light.
This is why Pauli strongly objected to the existence of "electron spin" in 1920's.
At that time, it is known that Eq.59 of Sommerfeld's model coincides with the experimental values in various atoms,
(Eq.59)
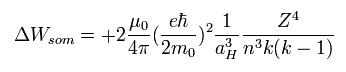
To prove the existence of electron spin, they needed to get Eq.59 by the spin-orbital interaction instead of relativistic mass change.
We suppose an electron is rotating around the +Ze nucleus.
From the viewpoint of the moving electron, the nucleus is rotating around the electron instead.
The speed of the nucleus is -v, and the coordinate of the nucleus is -r.
So according to Biot-Savart law, the magnetic field (B) at the point of the electron becomes,
(Eq.62)
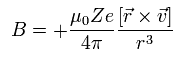
Here we introduce the angular momentum quantum number K (K = 1, 2, 3 ....).
This K satisfies the relation K ħ = m0r × v
So Eq.62 can be expressed as
(Eq.63)
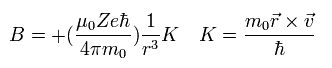
The magnetic moment of the spinning electron is g-factor (ge) × s (=1/2) × Bohr magneton.
So the interaction energy between the spinning electron and the magnetic field (B) becomes
(Eq.64)
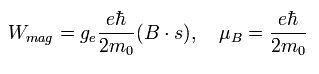
where μB is the Bohr magneton, s is the spin angular momentum (=1/2).
Substituting B of Eq.63 into Eq.64,
(Eq.65)
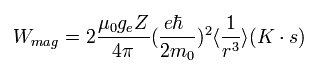
The energy difference between spin up (+1/2) and spin down (-1/2) states of Eq.65 becomes,
(+1/2 - (-1/2) = 1)
(Eq.66)
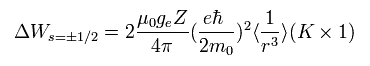
According to the Bohr's theory, the average value of 1/r3 satisfies
(Eq.67)
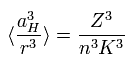
where aH is the Bohr radius, n means the energy level.
Substituting Eq.67 into Eq.66,
(Eq.68)
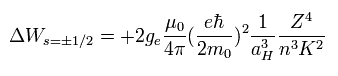
It was known that if K2 of Eq.68 was changed into k(k-1), the results agreed with the experimental values well.
(Eq.69)
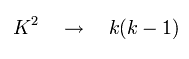
So substituting Eq.69 into Eq.68,
(Eq.70)
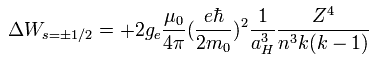
When the spin g-factor (ge) is 1, Eq.70 is just equal to Eq.59 (=Sommerfeld model).
But if the ge is 1, the electron magnetic moment becomes 1/2 × 1 = 1/2 × Bohr magneton.
So Eq.70 is wrong, because the electron magnetic moment must be 1 × Bohr magneton.
To solve this problem, L.H. Thomas appeared.
He had succeeded in justifying the electron spin using the Thomas factor 1/2.
(Though his method is a little complicated and "unnatural".)
Next we explain about this factor.
As shown on this page, the precession angular frequency of the spinning electron under the magnetic field (B) is
(Eq.71)
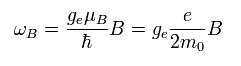
According to Bohr's correspondence principle, ħω = | W1 - W2 |.
So mutiplying Eq.71 by ħ,
(Eq.72)
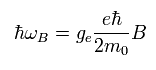
As shown in Eq.64, the interaction energy under the magnetic field (B) is
(Eq.64)
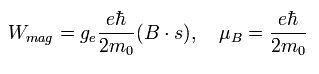
So the energy difference between s = ± 1/2 states under the magnetic field becomes
(Eq.73)
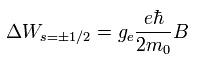
Eq.73 is just equal to Eq.72 !
Thomas found that when the electron is "accelerated", the electron's "specific" coordinate axis is "rotating" from the viewpoint of the "laboratory system".
According to his calculation results, the rotation angular frequency of this coordinate axis is
(Eq.74)
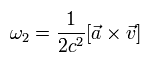
where a is the acceleration of the electron.
So the "true" precession angular frequency of the electron in the laboratory system is Eq.71 + Eq.74, as follows,
(Eq.75)
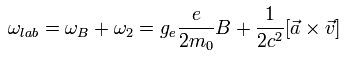
The electron's acceleration is caused by the Coulomb force of +Ze nucleus, as follows,
(Eq.76)
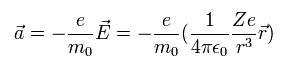
Here we use Eq.62 and μ0 of Eq.60.
(Eq.62)
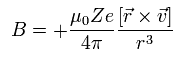
From Eq.76, Eq.62, and Eq.60, the total angular frequency of Eq.75 can be expressed as
(Eq.77)
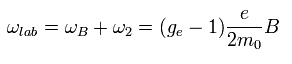
Using Eq.77, the interaction energy of Eq.64 under the magnetic field changes into
(Eq.78)
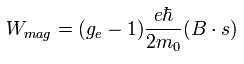
And Eq.70 changes into
(Eq.79)
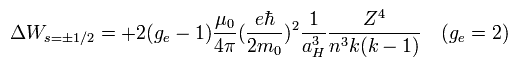
When ge is 2, Eq.79 is just equal to Eq.59 of Bohr-Sommerfeld model !
Eq.79 = 1/2 × Eq.70.
So this 1/2 is called "Thomas precession factor".
Finally, Pauli accepted Thomas's spin model "reluctantly".
( Finally, Thomas got Pauli's sanction about the electron spin.)
By the way, which fine structure do you think is more natural, Thomas's spin-orbital or Bohr-Sommerfeld model ?
If the fine structure is caused by the spin-orbital interaction, this model includes "many unnatural accidental coincidences" of the relativity and spin-orbital interactions. ( 2S1/2=2P1/2, 3S1/2=3P1/2, 3P3/2=3D3/2.........).
And the replacement ( K2 → k(k-1) ) of Eq.69 can be gotten "naturally" in Bohr-Sommerfeld as shown in Eq.59.
But in the spin-orbital interaction model, this replacemant of Eq.69 must be gotten from quantum mechanical "mathematical" trick like l(l+1).
Eq.72 using Bohr's correspondence principle is strange, too.
The two-valued experiment in 1975 showed that the fermions don't return by one rotation. (By two rotations, they return.)
So we should consider the angle of 4π as one cycle in the electron spin
This means that the angular frequency of Eq.72 becomes half.
But if Eq.72 becomes half, Thomas factor 1/2 becomes meaningless.
This includes self-contradiction.
As a result, it can be said that the spin-orbital interation model is a more "unnatural" thing than the Bohr-Sommerfeld model.
Recently, using the Penning trap [3] which can trap single electron, the anomalous magnetic moment was measured.
(Fig.5) Measurement of anomalous magnetic moment by Penning trap.
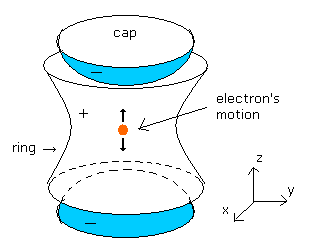
As shown in Fig.5, the Penning trap has the minus-charged (-) caps in the upper and lower parts.
And it has the plus-charged (+) ring around it.
So when the center is the origin, the electric potential of the Penning trap becomes
(Eq.80)
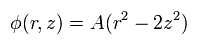
This means that the electron is attracted to the origin in the z direction by the force of
(Eq.81)
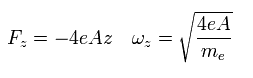
where ωz is the angular frequency in the z direction.
The electron is attracted outward by the positive-charged ring.
They apply a magnetic field (B0) in the z direction.
So the equation of the electron's motion in the x-y plane becomes
(Eq.82)
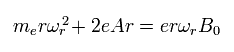
Eq.82 includes the centrifugal force and the Lorentz force.
To measure the spin magnetic moment, they need to add a small magnetic field of
(Eq.83)
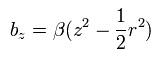
Due to the magnetic field gradient (2βz) of Eq.83, the magnetic moment of the electron receives the force of
(Eq.84)
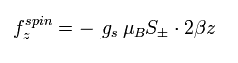
where μB is the Bohr magneton, S is the spin angular momentum (± 1/2), and gs is the spin g-factor.
(Eq.85) Bohr magneton.
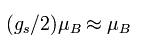
In the Penning trap, various motions are mixed as shown in Fig.6
So the electron's motion is very complex.
Of course, as the electron is very light, the influence of the thermal noise is very big.
(Fig.6) Axial, magnetic and cyclotron motions in the Penning trap.
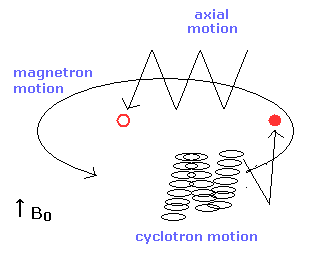
The magnetic force acting on the cyclotron motions of various quantum numbers is
(Eq.86)
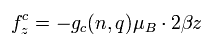
As a result, the total angular frequency in the z direction is
(Eq.87)
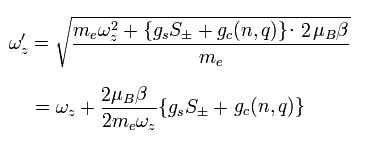
Furthermore, they apply weak oscillating potential ( V =K sin ω t ).
When this ω is equal to Eq.87, it causes "resonance".
This ω can be measured.
The electron spin is changing (flipping) randomly.
(Of course, the various cyclotron motions are changing randomly, too)
If they pick and measure the anglar frequency difference between ± S of Eq.87, they can get the exact spin g-factor [4].
But as shown in Eq.88, the magnetic moment caused by the minimum (ħ) orbital motion is the same as the spin magnetic moment.
(Eq.88)
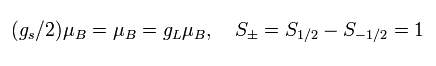
So if we use the minimum orbital motion instead of the "strange" spin, the g-factor becomes half.
(Only the interpretation changes.)
( References )
[1] W.H.Louisell, R.W.Pidd, An Experiment of the Gyomagnetic Ratio of the Free Electron, Phys.Rev.94 (1954) 7-16.
[2] D.T.Wilkinson, H.R.Crane, Precision Measurement of the g Factor of the Free Electron, Phys.Rev.130 (1963) 852-863.
[3] Dehmelt, Experiment with an Individual Atomic Particle at Rest in Free Space, Am.J.Phys.58 (1990) 17-27.
[4] H.Dehmelt, New Continuous Stern-Gerlach Effect and a Hint of the Elementary Particle, Z.Phys.D10 (1988) 127-134.
[5] V.Gerginov, K.Calkins, et.al. Phys.Rev. A 73 (2006) 032504.

2022/7/17 updated. Feel free to link to this site.