So he defined the average value of E of the black body, as follows,
(Eq.1)
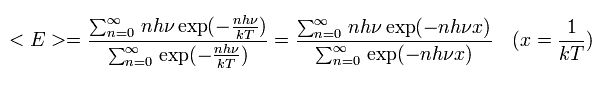
where the denominator is
(Eq.2)
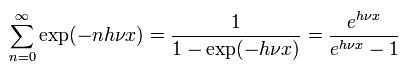
Top page (correct Bohr model including the two-electron atoms)
Electron spin is an illusion !
Quantum Hall effect by de Broglie wave.
Planck's constant (h) is very important concept, which is discovered by Max Planck in 1899.
Planck was investigating the black-body radiation.
If the hot object is black, meaning it absorbs all the light that hits it, then emits the thermal light in the equilibrium state.
According to Stefan-Boltzman law, the probability of the energy E state is proportional to exp (-E/kT), where T is temperature.
Planck hypothesized that the electromagnetic energy of the frequency (= ν ) is quantized ( E = nhν ).
So he defined the average value of E of the black body, as follows,
(Eq.1)
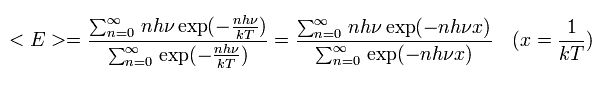
where the denominator is
(Eq.2)
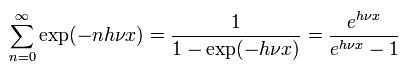
And the numerator of Eq.1 is
(Eq.3)
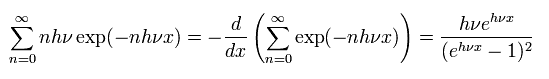
Inserting Eq.2 and Eq.3 into Eq.1, the average energy E is
(Eq.4)
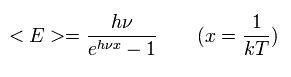
From the calculation result of Eq.4, Planck got the Planck constant of 6.55 × 10-34 Js, which is almost same as the latest value of
(Eq.5)
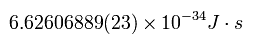
The relation of Eq.4 includes the equations of Rayleigh Jeans and Wien.
Planck constant of Eq.5 was gotten from Watt balance method, which is explained later.
(Steiner R et al, J. Res. Natl. Inst. Stand. Technol. 2005, 110, 1-26)
In 1905, Einstein proposed the photoelectric effect, and in 1916, Robert Andrews Millikan confirmed the Planck constatnt by the photoelectric effect.
His Planck value is 6.57 × 10-34 Js, which is almost same as Planck's hypothesis.
The important point is that Planck constant by Planck and Millikan are based on the de Broglie's relation of the electromagnetic wave.
And the Planck constants by the watt balance and Josephson effect are based on the electron's de Broglie's relation.
So this indicates that the quantized energy of the black body radiation originates from the electron's quantized de Broglie's waves.
Later, de Broglie's relation of the neutron was confirmed (Bragg's refrection), which is so precise as to be used to calculate the fine structure constant α, which Planck constant is almost same as the latest value of Eq.5.
It is known that the magnetic flux (Φ) is quantized, when it passes through a superconductor ring.
If the weak magnetic flux enter the superconducting material ring, the electron's current occurs in the boudary surface to cancel the applied magnetic field.
As a result, the magnetic flux density of the the superconducting material becomes zero. ( B = 0 ).
This is called "Meissner effect".
(Only in the part near the magnetic flux, the B is not zero, and the electron's current exists. )
(Fig.1)
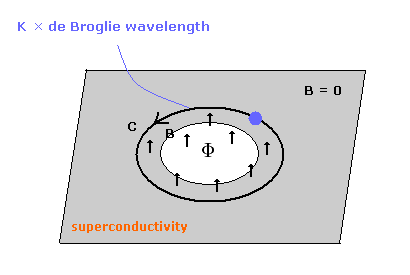
The magnetic flux quantum (Φ0) is the quantized magnetic flux passing through a superconductor.
The quantization of magnetic flux is closely related to the Aharonov-Bohm effect, but was predicted earlier by Fritz London in 1948 using a phenomenological model.
(Eq.6) Magnetic flux is quantized in a superconductor.
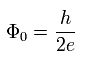
So using Eq.6, we can get the correct Planck constatnt (h).
First we try to get Eq.6 using Schrodinger equation.
To get Eq.6 in Schrodinger equation, we must hypothesize the "Cooper pair", which consists of two electrons.
(Is it possible that Cooper pair is a "artificial" thing ? )
In the superconductor at very low temperature, the phases of the all electrons become almost same, as shown in Eq.7.
But what on earth is this phase of an electron ??
(Eq.7) Electron's wavefunction in a superconductor.
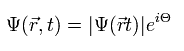
where the phase (Θ) consists of momentum (p) and energy (E), as follows,
(Eq.8)
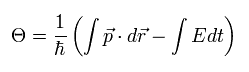
If we forget the repulsive force between two electrons, and suppose the "Cooper pair (= -2e )", the momentum (p) and the energy (E) become
(Eq.9)
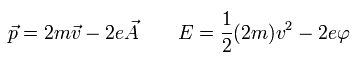
where we consider the Lorentz force. See also this page.
When we pay attention to only the space part. Eq.8 is
(Eq.10)
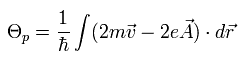
If we consider the phase of the wavefunction returns to its original, by rotating it around the hole of Fig.1,
(Eq.11)
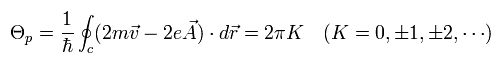
wehre K is an integer.
According to the Meissner effect, the magnetic field and electron's current in an superconductor can be ignored.
So we can suppose the electron's velocity (= v ) of Eq.11 is zero, as follows,
(Eq.12)

where Φ means the magnetic flux surrounded by the vector potential (= A ) according to Maxwell's law.
According to Aharonov-Bohm effect, the vector potential (= A ) exists in the parts where the magnetic flux density (= B ) is zero.
From Eq.12, the magnetic flux (Φ) in the hole becomes quantized, as follows,
(Eq.13)

wehre
(Eq.14)
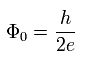
Eq.14 is called "magnetic flux quantum (Wb)", which is used to get correct Planck constant.
And the inverse of Eq.14 is called "Josephson constant".
By the way, we like to know what the phases really mean.
Here we suppose the electron is rotating around near the hole of Fig.1 to cancel the magnetic field.
When the centrifugal force is equal to the Lorentz force,
(Eq.15)
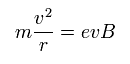
When one round of the orbit is equal to an integer times de Broglie's wavelength,
(Eq.16)
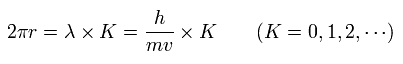
From Eq.15 and Eq.16, we can get
(Eq.17)
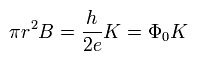
Eq.17 means the magnetic flux (Φ) passing through the hole of Fig.1, as follows,
(Eq.18)
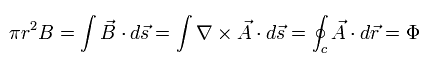
So we can get the quantized magnetic flux of Eq.13 and Eq.14 using de Broglie's wave + classical mechanical concept !
This means the "mysterious" phases are de Broglie's waves of the rotating electrons near the hole.
And surprizingly, we don't need to use the "strange" Cooper pair in Eq.15 and Eq.16.
Originally, "Cooper pair" is "intentionally" introduced to cancel the spin effect, I think.
(If the electron spin really exists.)
How do you think about it ?
(Fig.2) Josephson juction.
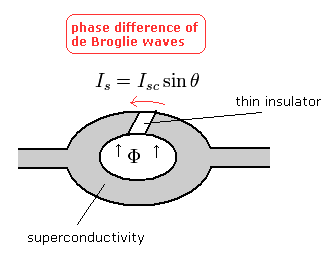
Josephson effect is a phenomena that occurs when two superconductors are placed in proximity, with some very thin insulating barrier between them.
The Josephson effect produces a current, known as a supercurrent, that flows continuously without any voltage applied, across a device known as a Josephson junction (JJ) or SQUID (= superconducting quantum interference device ).
This Josephson effect, SQUID (and superconducting qubits ) can be naturally explained by magnetic flux quantum based on quantized de Broglie wave theory of Bohr-Sommerfeld model ( this-p.1-2. this-p.9-10 ) irrelevant to quantum mechanical negative-kinetic-energy tunneling.
(Eq.19) Josephson current I
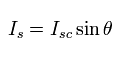
where the phase difference θ can be expressed as
(Eq.20)
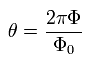
Eq.19 and Eq.20 mean that when the magnetic flux (Φ) in the hole is an integer times the magnetic flux quantum (= Φ0 = h/2e related to quantized de Broglie wavelength ), the phase difference becomes zero, and the Josephson currenct doesn't occur ( this p.5-7, this p.3 ).
So we can naturally say that the Josephson juction is influenced by de Broglie's waves of electrons near the hole.
The quantum tunnel effect is caused by de Broglie's wave of the electron instead of unrealistic quantum mechanical negative kinetic energy.
With a fixed voltage V across the junction, the phase will vary linearly with time and, the current will be an AC current.
(AC Josephson effect.)
According to Maxwell equation, the voltage of the ring in Fig.2 can be expresses as
(Eq.21)
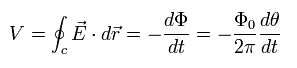
where we use Eq.20.
Integrating Eq.21 by time t, we can get
(Eq.22)
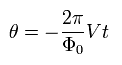
Substituting Eq.22 into Eq.19, we can get AC Josephson current of
(Eq.23)
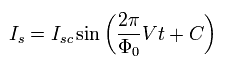
So the frequency of Eq.23 is
(Eq.24)
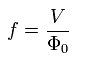
The frequency of Eq.24 can be confirmed by the microwave, which synchronizes with the AC Josephson current. (Shapiro step.)
This measured voltage (V) is used to give the definition of a volt.
And the Josephson effect can give the correct Planck constant (h), which is included in Φ0.
(Of course, this Planck constant originates from de Broglie's relation of the electron of Eq.16.)
Aharonov-Bohm effect is a quantum mechanical phenomenon in which an electrically charged particle is affected by an electromagnetic field, despite being confined to a region in which both the magnetic field B and electric field E are zero.
The underlying mechanism is the coupling of the electromagnetic potential with the complex phase of a charged particle's wavefunction.
The most commonly described case takes place when the wave function of a charged particle passing around a long solenoid experiences as phase shift as a result of the enclosed magnetic field, despite the magnetic field being negligible in the region through which the particle passes.
This phase shift has been observed experimentally.
First, we explain the AB effect by the quantum mechanical method.
(Of course, this uses the concept of "classical" Lorentz force.)
Using the vector potential (A) and scalar potential (φ), Hamiltonian of an electron under the electromagnetic field is
(Eq.25)
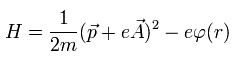
where we consider the Lorentz force. See also this page.
According to the Maxwell equation, the electric (E) and magnetic field (B) can be expressed as
(Eq.26)
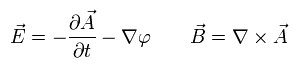
If we change the vector and scalar potential, as follows, the E and B can be expressed by new vector and scalar potential by the same relation of Eq.26.
(Eq.27)
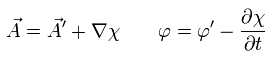
where χ is an arbitrary value.
( Try inserting Eq.27 into Eq.26. )
This is called "gauge transformation".
Next we express Eq.25 by Schrodinger equation, as follows,
(Eq.28)
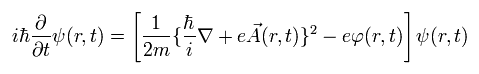
After the gauge transformation, the same Schrodinger equation as Eq.28 must be satisfied, as follows,
(Eq.29)
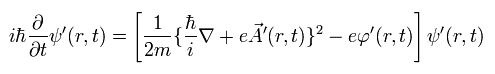
where we suppose the wavefunction after gauge transformation, as follows,
(Eq.30)
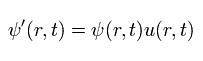
Using Eq.30 and Eq.27, the terms of the energy and scalar potential in Eq.29 can be expressed as
(Eq.31)
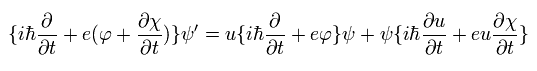
And the terms of the momentum and the vector potential in Eq.29 can be expressed as
(Eq.32)
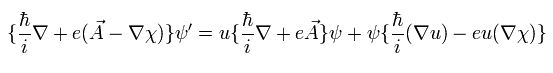
One more operator needs to be added to Eq.32, as follows,
(Eq.33)
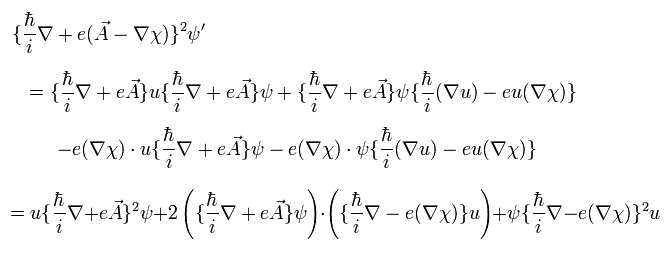
where ∇ inside of ( ... ) doesn't act on the functions outside of it.
Substituting Eq.31 and Eq.33 into Eq.29, if the next relations are satisfied, it agrees to Eq.28.
(Eq.34)
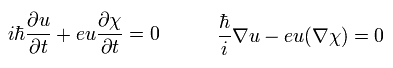
The solution of Eq.34 is
(Eq.35)
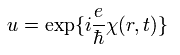
So Eq.30 becomes
(Eq.36)
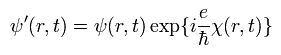
We suppose the magnetic field is confined inside of the solenoid, which radius is r0
(Outside of the solenoid, the magnetic field is zero.)
So the vector potential (A) can be expressed as
(Eq.37)
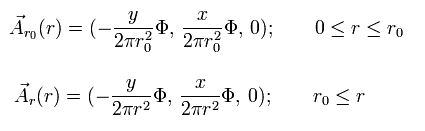
From Eq.26 and Eq.37, the magnetic field density (B) becomes
(Eq.38)
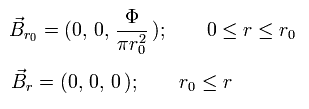
where
(Eq.39)
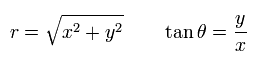
From Eq.37, the vector potential outside of the solenoid has only the "tangential" component, as follows,
(Eq.40)
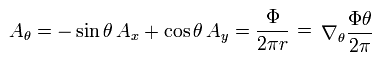
where
(Eq.41)
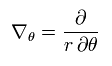
From Eq.40, if we suppose gauge χ of Eq.27 as follows, A' becomes zero.
(Eq.42)
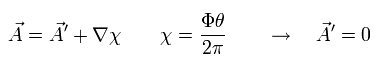
At this state, the original wavefunction becomes
(Eq.43)
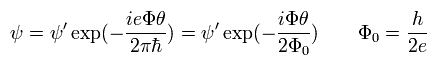
According to Eq.43, the phase of the wavefunction changes in the unit of 2 × Φ0.
(This result seems to be different from the above magnetic flux quantum.)
(Fig.3)
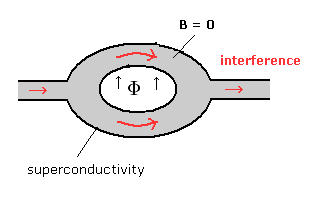
Instead of the long solenoid, we uses the superconductor, which can confine the magnetic flux only in the hole (and near the hole), as shown in Fig.3.
We send the electric current, change the magnetic flux (Φ) of the hole, and measure the electric resistance.
The electric currents from the two paths interfere with each other, which different patterns cause the change of the resistance.
The experimental result shows that the electric resistance changes in a cycle of 2 × Φ0.
This means that Schrodinger wavefunction of Eq.43 is correct ?
(Fig.4)
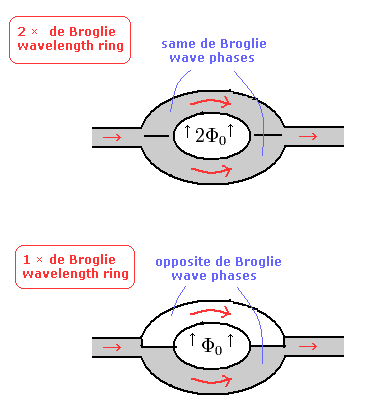
According to de Broglie's waves of Bohr model, when the magnetic flux is 2 × Φ0, 2 × de Broglie waves are included in one round of the orbit. (upper panel of Fig.4.)
In this case, the two electric currents are influenced by the same phase de Broglie's waves.
But when the magnetic flux is 1 × Φ0 (lower panel of Fig.4), the two electric currents are influenced by the different phase de Broglie's waves.
As a result, the interference pattern changes in a cycle of 2 × Φ0.
It is unnatural that the above Schrodinger equation doesn't use the Cooper pair (= -2e), though it is used in the sections such as Josephson effect.
On the other hand, de Broglie wave by Bohr model can explain Aharonov-Bohm (AB) effect very "naturally".
The most precise method to measure the Planck constatnt is "Watt balance".
Here we explain about the watt balance method, and investigate whether the hydrogen's energy levels can be expressed correctly using the Planck constant.
(Fig.5)
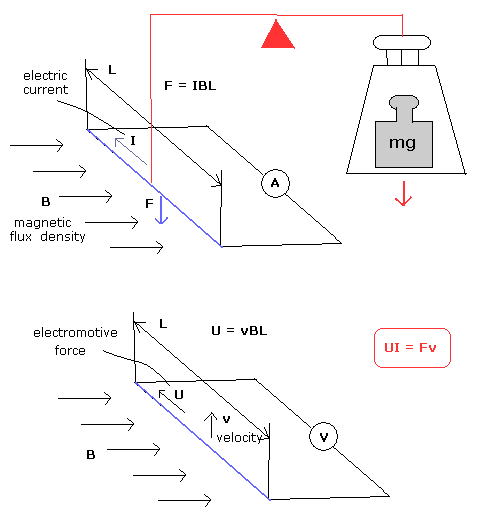
A conducting wire of length L which carries an electric current I perpendicular to a magnetic field of strength B will experience a force equal to IBL. (upper panel of Fig.5.)
The current is varied so that this force exactly counteracts the weight of a standard mass m, which is given by the mass multiplied by the local gravitational acceleration g.
To measure the current correctly, we need to use the "standard electrical resistance", which is defined by the quantum hall effect.
(See also Quantum Hall effect by de Broglie wave..)
In the two-dimensional electron systems subjected to low temperatures and strong magnetic fiels, Hall conductivity takes on the quantized value ( e2/h ).
(Planck constant of this Hall effect originates from de Broglie's relation of the electrons.)
This quantized value is used for the standard electrical resistance.
The same wire is moved through the same magnetic field (B) at a known speed v. (lower panel of Fig.5.)
By Faraday's law of induction, a potential difference U is generated across the ends of the wire, which is equal to vBL
Hence the unknown quantities B and L can be eliminated from the equations to give
UI = Fv
The above potential difference U is measured precisely by Josephson method of Eq.24.
As a result, we can get the very precise Planck constant, which originates from Josephson effect and Hall effect.
(So the watt balance method expresses the Planck constant of de Broglie's relation of an electron.)
The above watt balance method doesn't use the Rydberg constant, which can be gotten from atomic hydrogen spectrum.
So if we can calculate the correct experimental value of hydrogen atom using the above Planck constant of Eq.5, Planck constant from the watt balance method proves to be correct.
In Bohr model hydrogen, the centrifugal force is equal to the Coulomb force.
And the orbital length is an integer times de Broglie's wavelength, as follows,
(Eq.44)
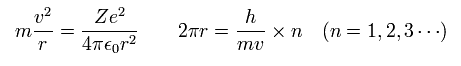
From Eq.44, we can get the radius (r), velocity (v), and the total energy (E), as follows,
(Eq.45)
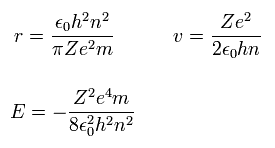
In the top page, we can get the precise new Bohr's helium result, which is equal to the experimental value.
In this new method, we calculate the Coulomb force and number of de Broglie's waves contained in the short movement section at short time intervals.
As a control, we try computing the Bohr's hydrogen ground state energy by this new Bohr's helium method.
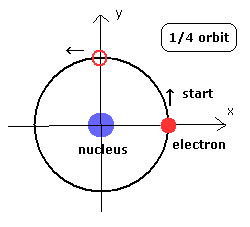
(Fig.6) Bohr's hydrogen 1S orbit.
sample JAVA program to compute Bohr's 1S hydrogen orbit
If you copy and paste the program source code inside into a text editor, you can easily compile and run this.
(This class file name is Hyatom, so save this text editor as "Hyatom.java", and compile it.)
In the above program, we use the next new units of
(Eq.46)
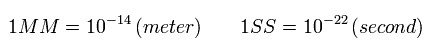
From Eq.46, the velocity and acceleration are
(Eq.47)
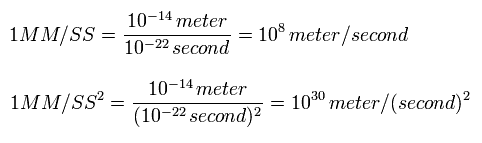
At the interval of 1 SS (= 10-22 sec ), we calculate the x and y components of the acceleration from Coulomb force, as follows,
(The orbit is supposed to be in the x-y plane.)
(Eq.48)
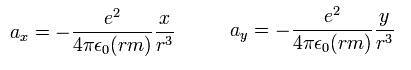
where (rm) means the reduced mass of hydrogen atom.
And at the intervals of 1 SS, we compute the number of de Broglie's waves contained in the short movement section, and sum them up, as follows,
(Eq.49)
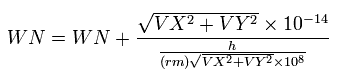
where the numerator means the movement distance (meter) for 1SS, and the denominator is de Broglie's wavelength (meter).
VX and VY mean the velocity components (MM/SS).
And the above program also calculate the theoretical values of the total energy |E| and radius (MM) using Eq.45.
The results are shown in Table 1.
When the last VY (the y component of the electron's velocity after 1/4 orbit) is zero, the electron's orbit becomes stable. (See Fig.6.)
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -13.580 | 5301.0 | 0.25017 | 1.00068 |
| -13.590 | 5297.0 | 0.25008 | 1.00032 |
| -13.5983 | 5294.5 | 0.25000 | 1.00000 |
| -13.600 | 5294.0 | 0.24999 | 0.99996 |
| -13.610 | 5290.0 | 0.24989 | 0.99956 |
The experimental value of the total energy is -13.59844 eV.
So the relativistic correction to the energy is -0.00014 eV, which is a proper value.
The theoretical value of the total energy from Eq.45 is -13.5983 eV
And the theoretical value of the radius from Eq.45 is 5294.65 (MM).
These theoretical values agree with the above calculation values of Table 1.
This means that the computational method used in the new Bohr's helium is correct, too.
If we don't use the reduced mass, the result becomes -13.606 eV, which is different from the experimental value.
So this proves that the electron and nucleus are actually rotating around the center of mass.
Planck constant h of the photon is the same value as that of electron's (or neutron's ) de Broglie's wave.
So can we get the photon (electromagnetic wave) quantized frequency from Bohr model hydrogen ?
Bohr's 1S orbit, the orbit is equal to one de Broglie wavelength, as follows,
(Eq.50)
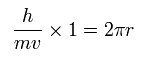
So the electron's frequency (= f ) can be expressed as
(Eq.51)
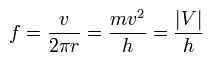
where we use the relation of
(Eq.52)
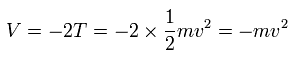
Eq.51 means that if we apply the electromagnetic wave of the frequency (f) of Eq.51, it synchronizes with the Bohr's 1S electron's motion.
As a result, the 1S electron is emitted keeping the "original" velocity (v).
So the frequency of the applied electromagnetic wave agrees with the amount to cancel the Coulomb energy, which binds the electron.
How about the 2S Bohr's electron ?
In the 2S, the orbital length is twice de Broglie's wavelength, as follows,
(Eq.53)
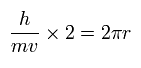
So the electron's frequency becomes
(Eq.54)
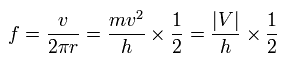
So this result is different from Eq.51.
But as the 2S orbit contains two de Broglie's wave phases, the wave phases return by 1/2 rotation.
So if we use π r instead of 2π r in the denominator of Eq.54, we can get
(Eq.55)
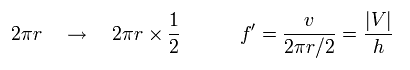
The result of Eq.55 is just equal to Eq.51 of Bohr's 1S orbit.
This means the frequency of the applied electromagnetic wave agrees with the electron's frequency, which cancels the Coulomb energy.
de Broglie's wave of each point on the electron's orbit is oscillating.
And in case of Eq.55, each point oscillates once, while the electron moves half of its orbit (= 1 de Broglie wavelength of 2S orbit.)
So it is thought that the electromagnetic wave acts on each point on the orbit.
(Fig.7) Emitted electromagnetic wave's frequency.
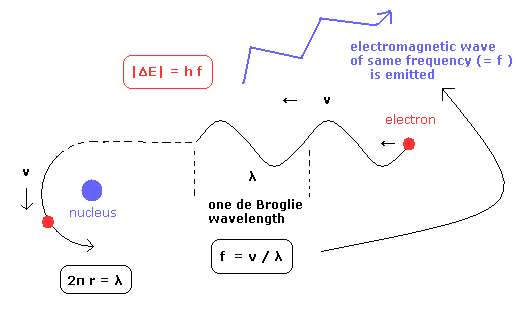
Next we consider the emitted electromangetic wave, when the free electron with the velocity v, which is equal to the Bohr's 1S electron, become bound to the 1S orbit.
(As a result, the velocity v is not changed. )
If we suppose the free elecron's de Broglie's wave frequency is equal to the emitted electromagnetic wave, it can explain the relation of E = hf, correctly.
So these results indicate that the electromagnetic wave's quantized frequency is related to Bohr's electron's de Brolie wave frequency.
And furthermore, if we also consider the kinetic energy change, the photoelectric effect can be explained by Bohr model and "classical" electromagnetic wave.
From the beginning, the kinetic energy of the electron is expressed as de Broglie's wave, so it can easily interact with the electromagnetic wave, as shown in Compton effect.

2011/6/20 updated. Feel free to link to this site.