(Fig.1) Quantum mechanics just artificially adjusting free parameters cannot predict any atomic energies.
Quantum mechanical Schrödinger equations for multi-electron atoms ( such as helium ) and hydrogen molecule ion (= H+ ) are unable to have true solutions or true wavefunctions to conserve the constant total ( ground-state ) energy E (in any different electrons' positions ), so quantum mechanical Schrödinger equations and wavefunctions proved to be false ( this p.2-upper, this p.7 ).
Quantum mechanical Schrödinger equation for only one-electron hydrogen atom can be solved, which solution agrees with successful Bohr atomic model.
Quantum mechanics, which is useless and unable to predict any atomic energies, just artificially chooses fake trial wavefunction or basis sets for unsolvable Schrödinger equations and manipulates various free parameters, which ad-hoc approximation is called variational methods ( this p.25 ).
Unsolvable Schrodinger equations have to find fake solutions giving the lowest atomic energies out of infinite choices of wavefunctions and parameters by approximate variational methods ( this-(2) ).
↑ But it is impossible to look into infinite numbers of parameters, so quantum mechanical (variatinal) methods are useless, unable to predict any atomic or molecular energies ( this p.2-2nd-last-paragraph ).
This-p.1-last says
"The (quantum mechanical variational) theorem does Not tell us (= cannot predict ) how far above the ground state energy"
If this variational methods, which should give the upper bound to a true ground state lowest energy, can find wrong solutions giving energies lower than actual atomic energies, the quantum mechanics is proved wrong ( this-21.1 ).
Actually, physicists can find these wrong solutions disproving quantum mechanics, so they deliberately fix some free parameters called exponent to artificially prevent their chosen fake solutions from giving energies lower than actual atomic energies.
(Fig.2) Quantum mechanics has to artificially choose free parameters to adjust calculated (fake) atomic energies, which cannot predict any true atomic energies.
In fact, in all these quantum mechanical (variational) methods for the unsolvable useless Schrodinger equations, physicists must deliberately manipulate free parameters (= exponent parameters k, ζ, ξ, η of e-kr, e-ζ r, e-ξr, e-ηr..) of artificially-chosen fake wavefunctions to seemingly obtain (fake) total energy close to experimental value ( this p.6-7 ), which is Not prediction of quantum mechanics.
This-p.1 says
"Hamiltonian (= Schrodinger equation's atomic energy ) that cannot be solved exactly and where
perturbation theory cannot be applied"
"One possibility is to use the variational principle: it does Not give you the exact answer but gives you an upper bound to the energy"
↑ If the current only quantum mechanical approximate method called variational method ( this-p.1~6 ) gives wrong energies lower than the true atomic energies (= break the upper bound ), it disproves quantum mechanics. ← This actually happened.
↑ Physicists need to intentionally fix the free exponent parameter k to some desirable values (= so quantum mechanics cannot predict atomic energies ), because if they try to find the exponent parameter k giving the lowest energy ( out of infinite choices ), this can give wrong energies lower than true atomic ground-state (= lowest ) energies ( this p.6-IV says The exponents are considered as adjustable parameters. ).
All Schrodinger equations for multi-electrons atoms such as Helium are unsolvable, useless, unable to predict true atomic energies.
Physicists have to rely on the illegitimate approximation called variational methods artificially choosing fake trial wavefunctions or basis sets with many freely-adjustable parameters to obtain the lowest (fake) total energies as possible.
Only in a two-electron Helium (or lithium ), physicists artificially choose Hylleraas-type (fake) trial wavefunctions including variables of interelectronic distance (= r12 = distance between two electrons-1 and 2, this-p.2 ), which can give (fake) total energies lower than other trial wavefunctions in variational methods.
The problem is that the calculation by this Hylleraas trial wavefunctions is impractical, too time-consuming to apply to atoms with more than three electrons.
↑ It means quantum mechanics can Not obtain energies matching experimental energies of atoms with more than three atoms, even in its illegitimate approximate (= variational ) methods.
Here we show that even the current best (artificially-chosen) Helium trial wavefunctions giving the lowest total energies rely on freely-adjustable parameters (= instead of finding the parameters giving the lowest possible energy ), which can Not predict (Helium) atomic energies in their quantum mechanical variational method ↓
This paper about the current best quantum variational method for helium ground-state energy's p.1-(1)(2), p.3-Table.I says "where αi, βi and γi are complex (free) parameters (= exponent parameters of the artificially-chosen helium Hylleraas wavefunctions ) generated in a quasi-random manner:.
↑ Just adjusting parameters by quasi-random manner giving the helium ground state energy means they can give wrong energies lower than true atomic energies, if they really try to find exponents parameters giving as low energies as possible out of infinite parameter choices, which means quantum mechanics is wrong )"
This paper-p.12-2nd-paragraph says
"Also, I know of no published theoretical attempts to explain the excellent convergence found by Korobov with his highly nonlinear fitting of the
trial wavefunction..
Korobov’s approach may be likened to the work of fitting the Hydrogen
radial wavefunction with a set of gaussians, using floating exponents.
This sounds plausible, but at present it is just more handwaving about flexibility."
This other paper (= one of today's best quantum variational methods for helium ground-state energy )-p.4-left-last-paragraph also says
"The orbital exponent may be treated as a nonlinear (= exponent ) variational parameter,
though this is Not strictly necessary (= they don't try to find the lowest energy by using exponents as strictly-variational parameters )"
p.5-(24), p.9-Table.V intentionally fixed one non-linear parameter β = 1 and another exponent parameter α = 2.20 (= if they more strictly vary these parameters, they could find fake energies lower than true ground state energies ).
Schwartz intentionally fixed an exponent parameter k to 3.5 (= k is Not used as a variational parameter finding the lowest energy, this-introduction-(3), p.1147-Results says the parameter k was fixed at the artificially-chosen value of 3.5 ) to illegitimately obtain Helium ground-state energy by quantum variational method.
Also in the recent calculation, he fixed (= instead of vary ) the exponent parameter k at (the artificially-chosen value of ) 2.0, which was used as an adjustable scale parameter (= to prevent the calculated values from getting lower than true helium energy ) not as a true variational parameter giving the lowest possible energy in obtaining helium ground state energy based on Hylleraas trial wavefunctions ( this p.2-(0.3) ).
Another research also intentionally fixed exponent parameters (= η, ζ ) of helium Hylleraas wavefunctions at (artificially-chosen values of) 6.00 or 6.50 ( this-p.6-lower~p.7-Table.1 ) to deliberately prevent their calculated energies from being lower than true helium ground-state (= lowest ) energy.
Drake also treated the exponent nonlinear parameters as freely optimized scale factors ( this p.4-Table.IV ).
↑ It means quantum mechanical variational methods can get wrong energy values lower than true ground state energies (= in atoms such as helium ) if physicists use various forms of wavefunctions (= including interelectronic distance like Hylleraas ) and really try to find parameters giving the lowest possible energies.
So they intentionally fixed those (exponent) parameters at some round numbers (= like exponent scale parameter k = 2.0, this-p.2-(0.3) ) to avoid lowering the calculated values below the true ground state energies. ← fake variational method
This p.1-introduction-4th-paragraph (and p.5-Table.1 ) says "However, according to recent experimental result (Bergeson et al., 1998), the results from the techniques reported above overestimated the helium ground-state energy" ← Quantum mechanical variational methods turned out to be Not variational, so false.
(Fig.3) Quantum mechanical unsolvable Schrodinger equations have to artificially choose fake unphysical trial wavefunctions in the impractical CI.
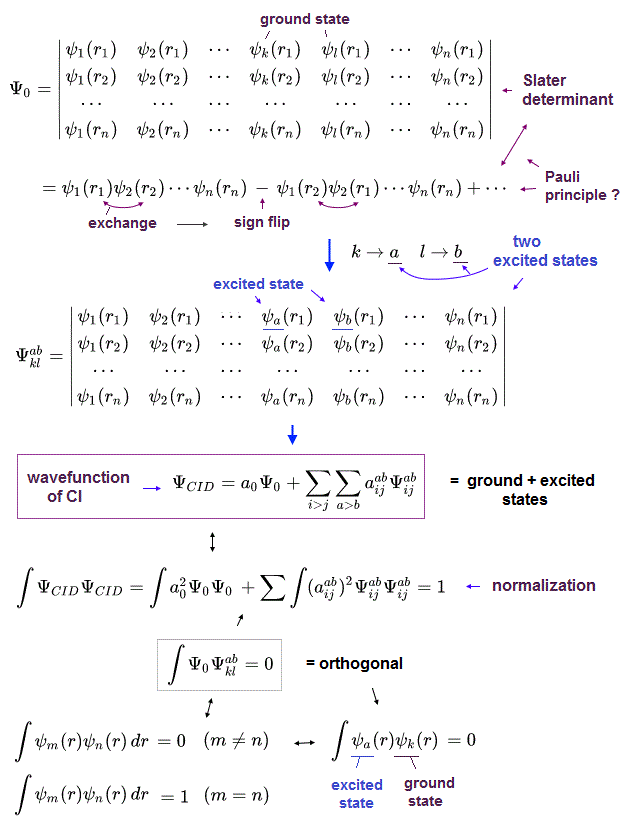
Quantum mechanical ( artificially-chosen ) wavefunctions (for unsolvable useless Schrodinger equation ) obeying the ad-hoc Pauli principle must be expressed as (unphysical) antisymmetric wavefunctions or Slater determinants, whose Schrodinger energy approximate calculation is called Hartree-Fock (= HF ) equations ( this p.6 ).
These quantum mechanical approximate Hartree-Fock (= HF ) or molecular orbital methods are known to be unable to give the total energies close to experimental values even in their chosen trial wavefunctions. ← the difference between this Hartree-Fock equation and true energy is called correlation energy.
The current most-widely used quantum mechanical approximate methods to seemingly get this correlation energy beyond Hartree-Fock is one-pseudo-electron density functional theory (= DFT ) that just artificially chooses fictitious exchange-correlation energy functional and pseudo-potential ( this-p.3-5 ), so DFT is fake ab-initio unable to predict any values.
The unsolvable useless quantum mechanical Schrödinger equations have to rely on the impractical time-consuming approximation called configuration interaction (= CI, this-p.5-last ).
In this impractical (full) CI, the artificially-chosen trial (fake) wavefunctions (= ΨCID ) are expressed as the linear combination of more than one (unphysical) antisymmetric Slater determinants ( this-p.3-4, this-p.21 ).
This impractical CI includes the fictional excited atomic wavefunctions ( this-p.8, this-p.8 ).
They artificially choose and adjust these fictitious exchange and ground-sate atomic trial wavefunctions to give lower (fake) total energies.
↑ The main components of this CI (illegitimately) lowering total energy is the (unreal) exchange energies between (artificially-excited) electrons ( this-p.30-37 ).
Because the artificially-chosen excited and ground-state trial wavefunctions are often orthonormal to each other (= integral of these wavefunctions are artificially made to be zero ), which cannot make the exchange energy between two (fictitious) electrons zero ( this-p.1,7, this-p.3 ). which remain as the (fictitious) correlation energy.
↑ Even this impractically time-consuming full CI cannot give (fake) total energies matching experimental values, because multi-electron atoms with more than three electrons cannot use Hylleraas wavefunctions that can give wrong energies lower than the true atomic energies, which disproves quantum mechanics.
(Fig.4) Coupled cluster (= CC ), which is Not variational, can give wrong energies lower than true ground state energy, so CC is Not a right theory.
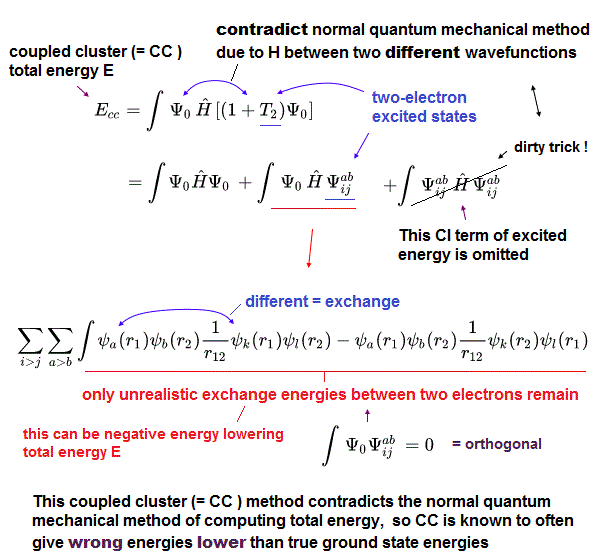
Instead of impractical time-consuming configuration interaction (= CI ), one of the impractical time-consuming approximations called coupled cluster (= CC or CCSD ) theory is often used.
The point is this coupled cluster (= CC ) theory contradicts the original Schrödinger equation, and can give wrong energies lower than the true ground state energies, which means CC is intrinsically a false theory (= CC is Not variational method, though the orthodox quantum variational method is also wrong ).
This-(6.30) says
"The result is a set of equations which yield an energy that is not necessarily variational (i.e., may Not be above the true energy)" ← Coupled cluster (= CC ) is false.
This p.1-left-1st-paragraph says
"it is worth noting that
CCSD (= coupled-cluster with singles and doubles ) is Not variational, and it is also Not guaranteed
to give real-valued energies"
This p.16-top says
"Consequently, the total CC energy is Not necessarily above the
exact ground-state total energy, just as in perturbation theory"
In CC, total energy (= E ) is given in a wrong way putting Hamiltonian energy equation (= H ) between two different wavefunctions like E = ∫Ψ0HΨab (← Not a normal ∫Ψ0HΨ0 or ∫ΨabHΨab, this p.18-(3.15), this p.27-2.29, p.29-2.40 ), which is the trick of CC lowering the total energy illegitimately faster than CI.
The (fake) total energy of the illegitimate CC can be lowered by the unphysically-negative exchange energy between two electrons of ground state and excited state (= ∫ψaψb1/r12 ψkψl, this p.8, this-p.7-lower, this-lower, this-(4) ) like CI.
↑ This means CC deliberately omits the annoying positive excited energy part to illegitimately lower the total energy than CI.
So CC is known to be able to get total energy lower than true ground state energy (= CC is Not variational ), which fact invalidates CC method.
There are many cases where coupled cluster (= CC, CCSD, CCSDT ) disagreed with experimental results.
This p.5-3rd-paragraph says
"The CCSD model systematically overestimates all core excitation energies".
This p.36-3rd-paragraph says
"CC fails for systems
with strong static correlation"
This-abstract-last says
"CCSD(T) overestimates the formation energy"
This p.6-left-2nd-paragraph says
"CCSDT we observe partially strong overestimation of the
total energy"
(Fig.5) MP2 is not variational, because it can give wrong energies lower than true atomic energy illegitimately.
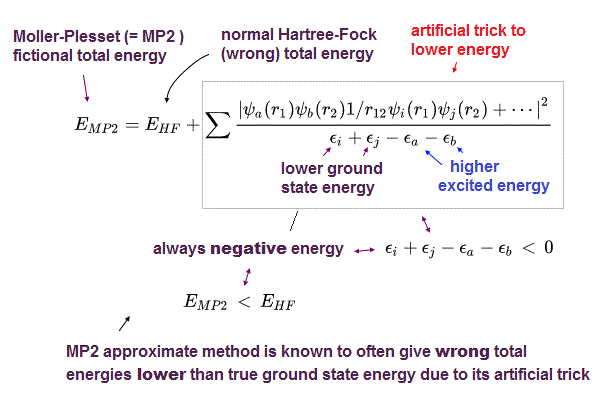
Instead of extremely-time-consuming configuration interaction (= CI ) and coupled cluster (= CC ), one of the illegitimate quantum mechanical approximations called Møller–Plesset perturbation theory (= MP) is often used to give the total energy lower than Hartree-Fock (= HF ) energy using deceitful tricks.
As shown in above figure, MP2 total energy (= EMP2 ) is always lower than Hartree-Fock energy (= EHF ) due to the artificially-introduced second term that is always negative.
The problem is this MP or MP2, which perturbation method (= PT ) is Not variational theory, often gives wrong energies lower than true ground state energies (= overestimation of energies, this abstract-last, this p.7-2nd-paragraph ), which means Møller–Plesset perturbation theory is an unreal theory.
This p.12-last says
"the MPn methodology is Not variational – it is possible that the
MP2 estimate for the correlation energy will be too large instead of too small."
This p.10-last says
"MP theory uses a truncated Hamiltonian, and is therefore Not
variational. That means that one cannot use the calculated energy as a measure
of the quality of the calculation."
This introduction-2nd-paragraph says
"Despite this popularity, the limitations of MP2-like methods are also well-known. In particular, they fail spectacularly for strongly correlated or metallic systems. Furthermore, a strong overestimation of dispersion interactions is observed for large polarizable systems"
This 1st-paragraph says
"it suffers from the usual MP2 overestimation of dispersion."
This p.2-2nd-last-paragraph says
"Thus, the value of E(2), the first perturbation to the Hartree-Fock energy, will always be negative. Lowering the energy is what the exact correction should
do, although the Møller-Plesset perturbation theory correction is capable of overcorrecting it, since it is not variational"
↑ As shown here, Møller–Plesset perturbation theory (= MP2 ) is a defective illegitimate theory.
As a result, all the quantum mechanical methods are wrong, illegitimate and useless theories which must be replaced by the realistic simple useful atomic model.
Feel free to link to this site.
