Top page (correct Bohr model )
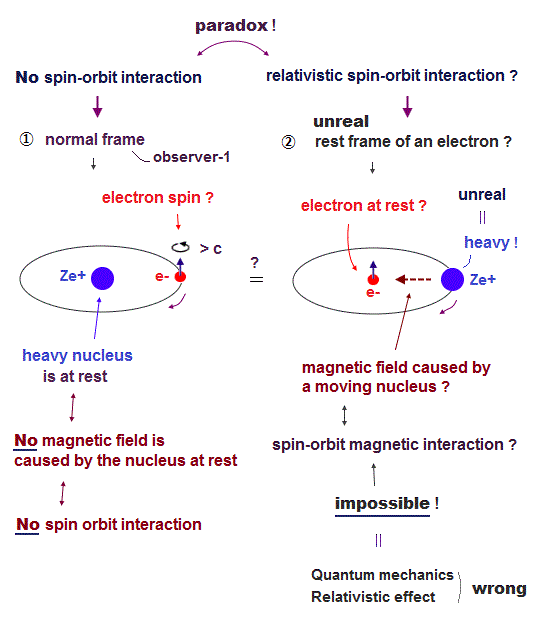
Strange "spin" is NOT a real thing
Fine-structure by Bohr-Sommerfeld model.
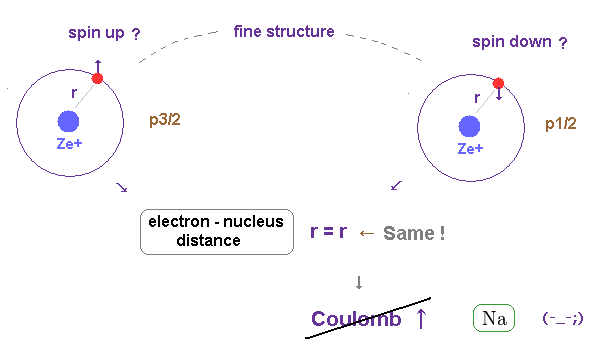
(Fig.1) Spin-orbit interaction is completely false.

As shown on this site and this site, it is said that sodium D lines are due to spin-orbit interaction , which is one of relativistic effects.
But on this page, we can prove spin-orbit coupling is too weak to explain alkali metals such as Na, K, ...
So spin-orbit coupling is completely an illusory concept.
(Fig.2) Dirac's hydrogen = Bohr-Sommerfeld model.
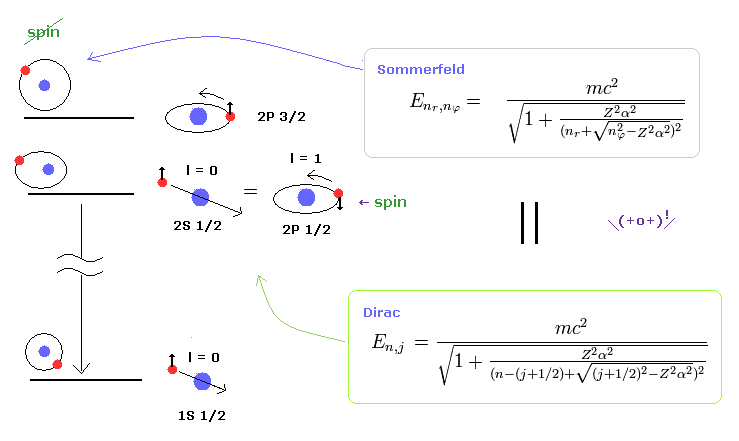
As shown on this site and this site (p.12) , Bohr-Sommerfeld model gives completely the same fine structure as Dirac hydrogen.
Compare this page (= Dirac hydrogen ) and this page (= Sommerfeld model ).
This accidental coincidence is very artificial.
Of course, Sommerfeld model appeared earlier than Dirac equation, so it is obvious that the latter solution imitates the former one.
About the Dirac hydrogen solution, see this site (p.9) and this site (last eq.).
(Fig.3) The same approximate fine structure formula.

On this site (p.9) and this site (p.13), we can get the simple form of energy difference (= fine structure ), which is proportional to Z4/n3.
"Z" is effective central charge, which includes all other charges of nucleus and inner electrons.
And "n" is the principal quantum number, which expresses major energy levels.
In this section, we have derived this approximate formula from the original Dirac (= Sommerfeld ) hydrogens.
(Fig.4)
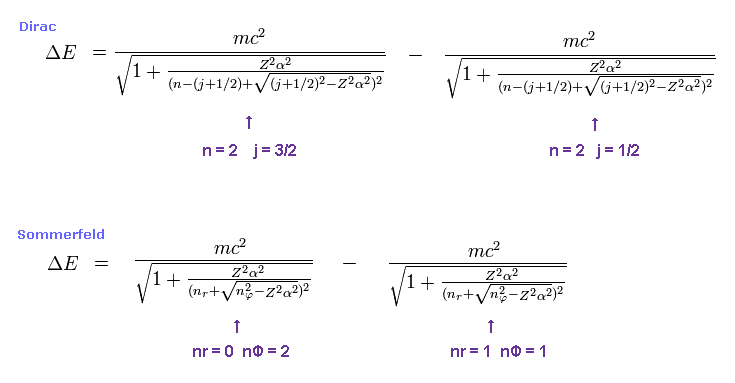
For example, first we get the energy difference between 2p3/2 and 2p1/2 of hydrogen atom.
The principal quantum number "n" is "2" in both states.
Total angular momentum is j = 3/2 in 2p3/2, and j = 1/2 in 2p1/2.
In Bohr-Sommerfeld model, radial number nr = 0 (1) and angular number nφ = 2 (1) corresponds to 2p3/2 (2p1/2).
(Fig.5) ↓ This formula gives the same results.
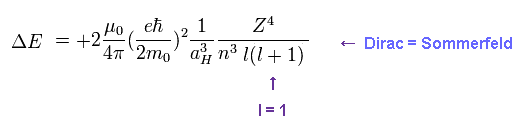
Approximately, we can use Fig.5 instead of the results of Fig.4 as fine structure.
When substituting l = 1 ( angular momentum in Dirac form ) into Fig.5, this formula gives the fine structure between 2p3/2 and 2p1/2.
Of course, Bohr-Sommerfeld model gives completely the same form of Fig.5.
Though Bohr model does NOT have spin, these two models are based on the same mechanism ?
This is a very strange coincidence !
(Fig.6) Hydrogen fine structure.
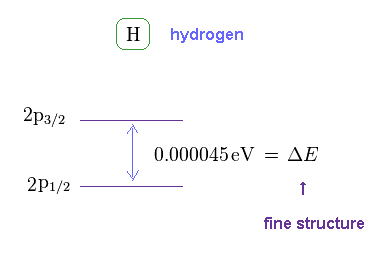
As shown on this site, hydrogen fine structure (= doublet ) between 2p3/2 and 2p1/2 is about 0.000045 eV.
This is a very small value, from which we find spin magnetic moment (= Bohr magneton, again coincidence ! ) is too weak to explain important physical phenomena.
(Fig.7) Energy unit conversion.
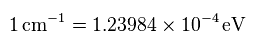
When you see hydrogen energy levels of Nist, energy unit of cm-1 is used instead of eV.
So using this site, we convert the unit of cm-1 into eV (= electronvolt ).
(Fig.8) Nist hydrogen energy data.
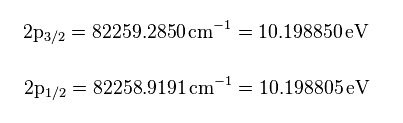
From the hydrogen energy levels of 2p3/2 and 2p1/2 in Nist, we can get the values of Fig.8 in eV.
So the energy difference between these two states becomes
(Fig.9)
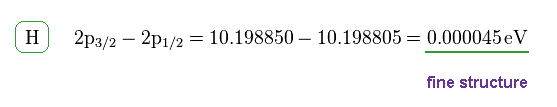
This energy difference is called fine structure, which is the same as Fig.6.
As shown in this section, this energy difference (= ΔE ) can be expressed as the simple form of Fig.10.
(Fig.10) Fine structure
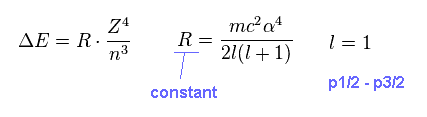
On this page, we investigate whether the equation of Fig.10 is always valid in various atoms and ions.
(Fig.11) Fine structures of H and He+
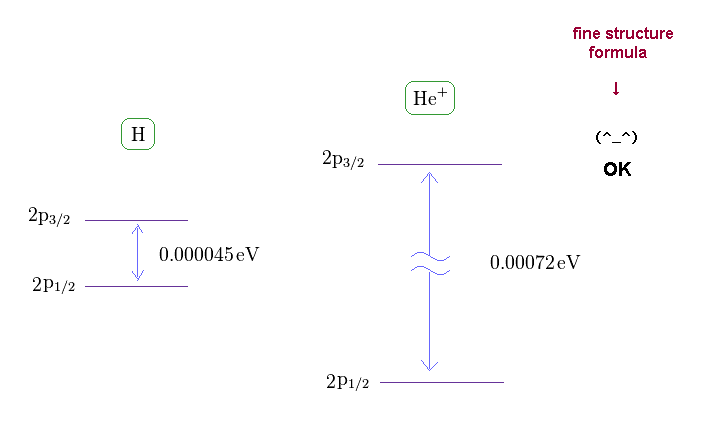
If you see this site, you find the energy difference between 2p3/2 and 2p1/2 in singly ionized helium (= He+ ) becomes 0.00072 eV.
(Fig.12) Central charge Z
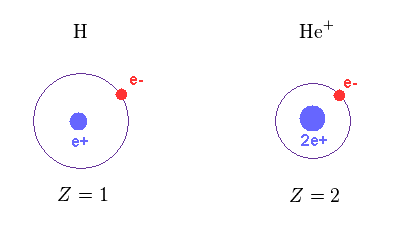
As shown in Fig.12, the central positive charge Z in H and He+ are Z = 1 and Z = 2, respectively.
(Fig.13) Computing each fine structure.
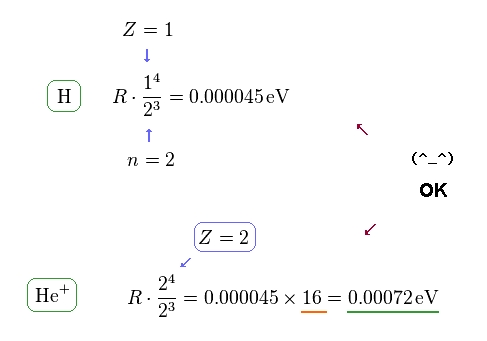
Using the formula of Fig.10, we find this formula is true in both hydrogen and helium ion.
Because the energy difference of He+ (= 0.00072 eV ) is about 16 times larger than hydrogen (= 0.000045 eV ).
This value of 16 is equal to Z4, when substituting Z = 2 into this energy formula.
In this section, we can confirm this formula is correct using JAVA program.
(Fig.14) Fine structure of Li and Be+.
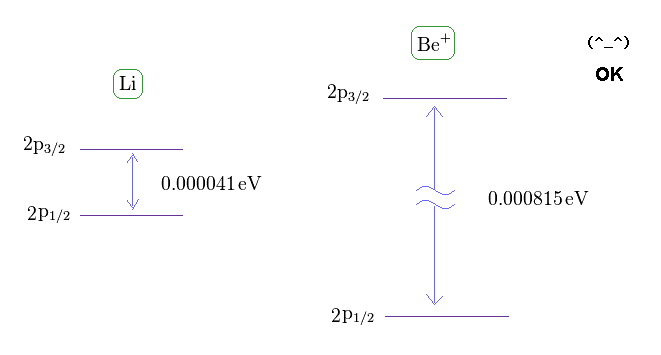
From this site and this site , we can know the energy difference between 2p3/2 and 2p1/2 in lithium and Beryllium ion.
(Fig.15) Central charge of Li and Be+ are close to H and He+.
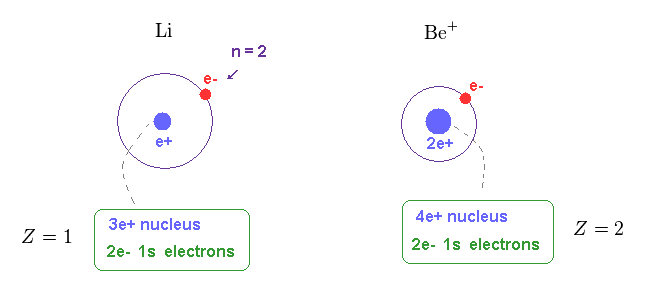
Of course, the central core charge of lithium atom is Z = 1.
Because this central charge Z includes all charges of nucleus and inner electrons.
In the same way, the central charge of Be+ should be close to Z = 2 like He+
(Fig.16) Fine structure formula is effective also in Li and Be+.
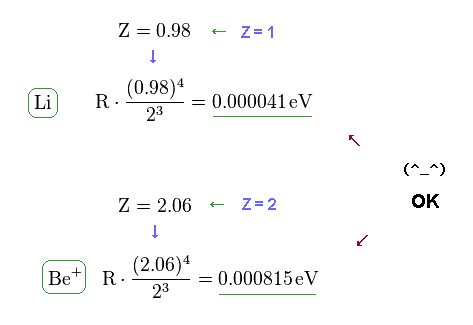
Using the formula of Fig.10 (= Fig.3 ) or computing values by program, we find this fine structure equation is valid also in lithium and beryllium ion.
(Fig.17) Sodium fine structure is too big to be explained by a single electron's spin.
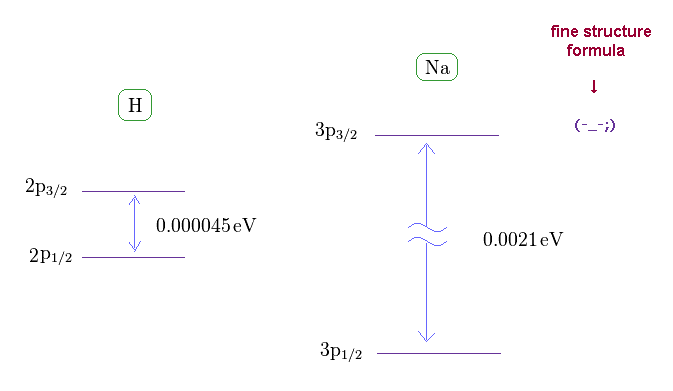
As shown on this site, hydrogen fine structure (= doublet ) between 2p3/2 and 2p1/2 is about 0.000045 eV.
On the other hand, the fine structure between 3p3/2 and 3p1/2 of sodium is as big as 0.0021 eV, as shown on this site.
Approximately, we can consider the outer 3p ( or 3s ) electron of sodium is moving around Z = +1 central core charge.
( "Core" is the total charge of Na nucleus and all electrons contained in n = 1 and 2 orbits. )
From the viewpoint of this outer electron, the core charge is moving around in the opposite direction, which causes magnetic field at the point of the electron having "spin".
As a result, spin-orbit interaction is produced, they insist.
(Fig.18) Central charge Z = 3.54, which is much bigger than Z = 1 in Na !?
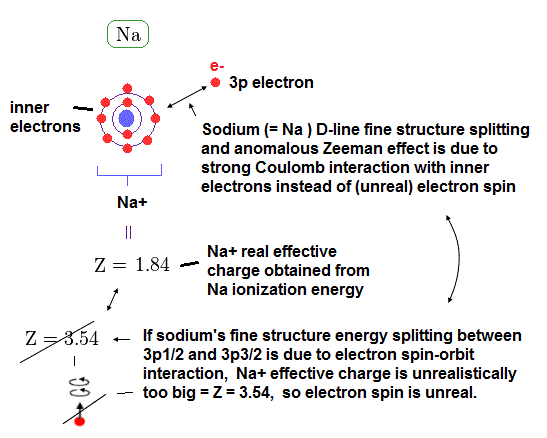
Both in hydrogen and sodium's outer (= 3p ) electron, the effective central (= core ) charges they feel are about Z = +1e.
Because this central charge Z is the sum of nucleus and all inner electrons.
But the discrepancy between these H and Na spin-orbital interactions are too wide.
This means the effective central charge in sodium is much bigger than Z = 1 (= about Z = 3.54 in Na ), which is very unreasonable and unrealistic.
(Fig.19) Effective "Z" becomes too big (= 3.5 ), if spin-orbit coupling is true.
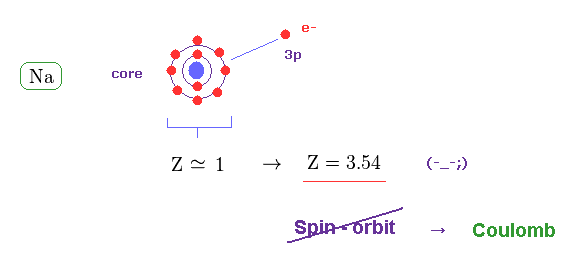
The central charge which 3p valence electron can feed should be close to Z = 1 also in sodium (= Na ).
But when Z = 1, the calculated spin-orbit energy becomes too small, which cannot reach 0.0021 eV.
When Z = 3.54, the fine structure formula gives this 0.0021 eV.
This result proves the spin-orbit coupling does NOT happen in actual fine structure.
(Fig.20) True effective charge Z = 1.84 from ionization energy.
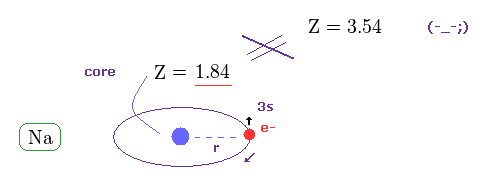
As shown on this site, the ionization energy of Na is 5.14 eV ( n = 3 ).
Comparing this value with hydrogen (= 13.606 eV in n = 1 ), we find the true effective charge of Na is Z = 1.84.
This Z is a little bigger than Z = 1 due to the wide gap of n = 2 inner electrons' shell.
But of course, it cannot reach Z = 3.54 at all.
(Fig.21) Wide discrepancy in Na and Mg+ fine structure.
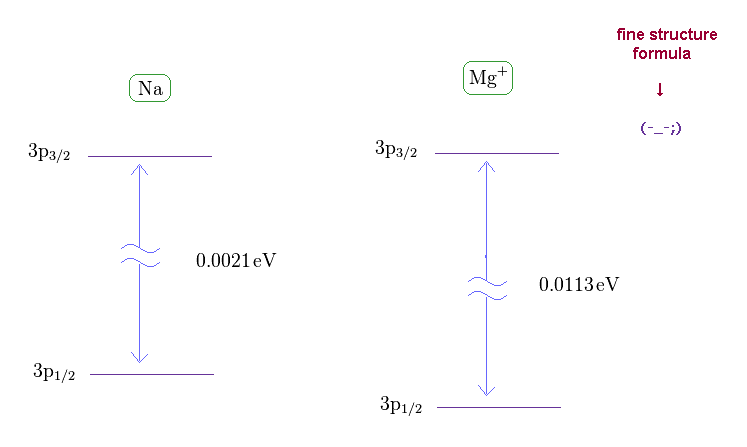
On this site (= Na ) and this site (= Mg+ ) , we can know the energy difference between 3p1/2 and 3p3/2 in Na and Mg+ (= singly ionized magnesium ion ).
(Fig.22) Effective central charge Z become too big in Na and Mg+.
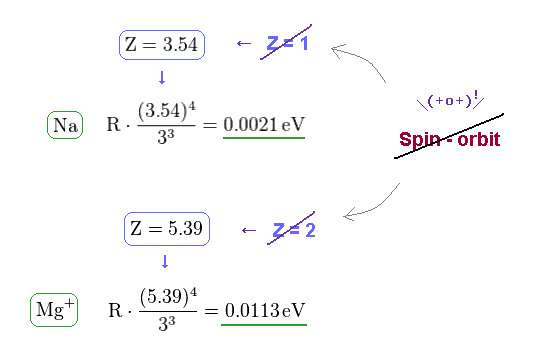
From Fig.21 and the fine structure formula, we find the effective central charge of Na and Mg+ become unrealistically too big.
Z of Na and Mg+ are 3.54 and 5.39, which is much bigger than 1 (= H ) and 2 (= He+ ).
(Fig.23) Unrealistic effective central charge Z.
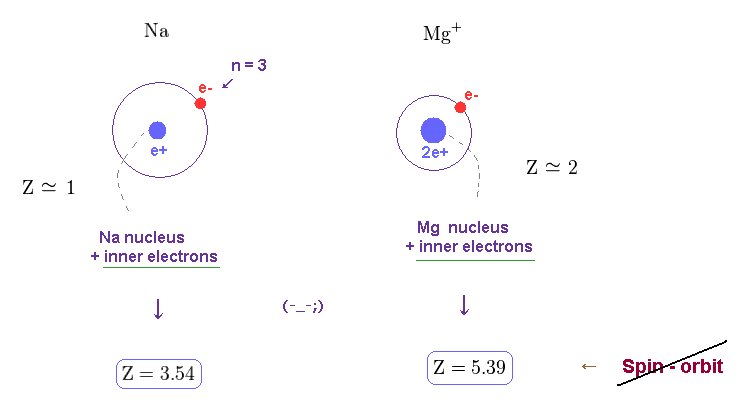
As I said, this effective central charge Z includes all charges of nucleus and inner electrons.
So Z of Na and Mg+ must be close to "1" and "2".
These results show the concept of spin-orbit coupling breaks down in various metals.
As shown on this page, in larger atoms such as K, Cs .., this result becomes much worse, which means Z becomes much more unrealistic values.
(Fig.24) Wider gap in n=2 electron's shell than n = 1.
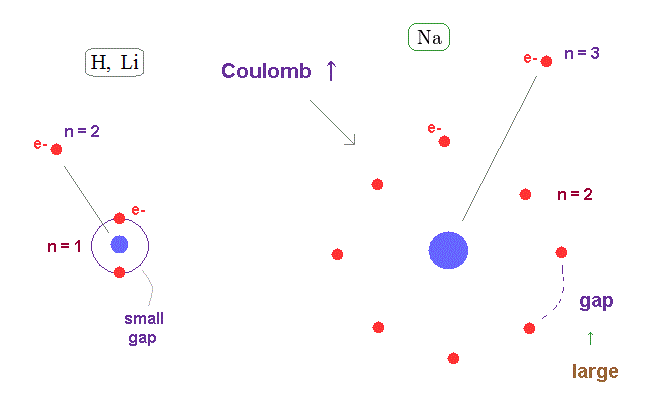
The average orbital radius of n = 2 is much longer than n = 1.
( Atomic radius is proportional to a square of n ).
So the valence electron of n = 3 in Na can feel much stronger Coulomb force through wider gap in n = 2 inner electron's shell than hydrogen and lithium.
This wider gap in inner electron's shell is the main reason why fine structure in metals become large.
We have to consider Coulomb effect instead of (imaginary) spin-orbit interaction.
(Fig.25) The difference in orbital shapes (= elliptic and circular ) causes large fine structure.
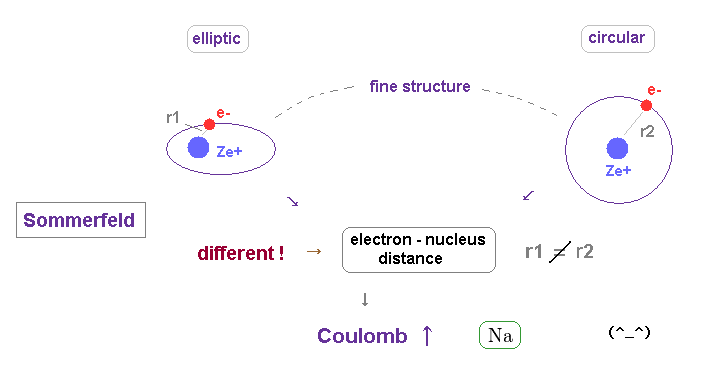
As shown on this page, the fine structure of Bohr-Sommerfeld model is cuased by the different orbital shapes in elliptical and circular orbits.
The average radius of them are the same in hydrogen.
But the perihelion of elliptical orbits is much closer to nucleus than that of circular orbit, which causes the different Coulomb interaction.
(Fig.26) Spin-orbit model cannot cause large Coulomb difference.
On the other hand, if this fine structure is generated by spin-orbit coupling, these two states must have the same orbital shape ( ex. 3p ).
The same orbital shape means there are NO difference in Coulomb interaction.
So spin-orbit coupling model cannot explain large fine structure in metals.
As a result, the fine structure of Bohr-Sommerfeld model proves to be true and real.
(Fig.27) Fine structure by original equation (= Dirac and Sommerfeld ).
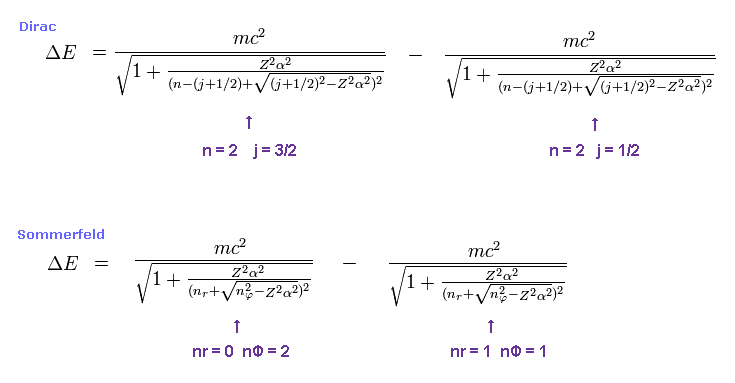
In this section, we compute two equations of Fig.27 and Fig.28 using this JAVA program.
Compile this program as the name of "finest.java".
(Fig.28) Fine structure by Z^4/n^3 form.
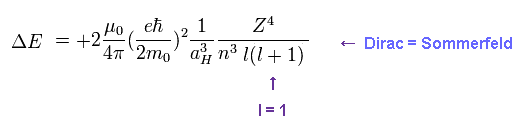
First, we try to compute fine structure of hydrogen (= energy difference between 2p3/2 and 2p1/2 ).
After running this program, input "1" (= Z ), press enter key.
This Z means the central charge.
Next, we input "2" (= n ) as the principal quantum number, and press enter key.
Lastly, input "1", which means we want to compute the energy difference between j=3/2 (= p3/2 ) and j=1/2 (= p1/2 ).
(Fig.29) Input each value. Hydrogen 2p3/2-2p1/2 case.

The computing results become like Fig.30.
The value of "finestructure by original equation" is gotten using Fig.27.
The value of "finestructure by Z^4/n^3 form" is gotten using Fig.28.
(Fig.30) Computing results.
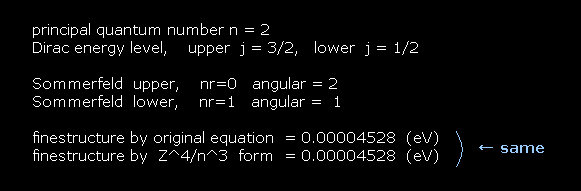
As you see Fig.30, the formula of Fig.27 and Fig.28 give the same results.
This means the approximate fine structure form of Z4/n3 is right.
(Fig.31) He+ ion case.
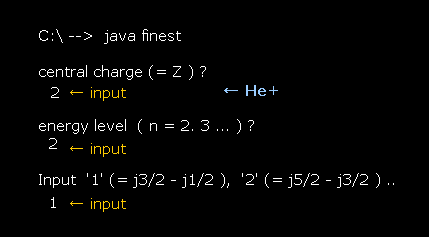
In He+ ion, input Z = 2 instead of Z = 1 in the first question.
Again the formula of Fig.27 and Fig.28 can give almost the same values.
(Fig.32)
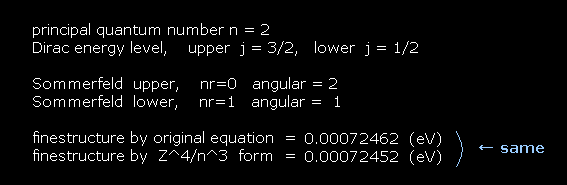
(Eq.1) Dirac's hydrogen = Bohr-Sommerfeld model.

As shown on this site and this site (p.12) , Bohr-Sommerfeld gives completely the same fine structure as Dirac hydrogen.
Compare this page and this page .
This accidental coincidence is very artificial.
About the Dirac hydrogen solution, see this site (p.9) and this site (last eq.).
(Eq.2) The same approximate fine structure formula.

On this site (p.9) and this site (p.13), we can get the simple form of energy difference (= fine structure ), which is proportional to Z4/n3.
"Z" is effective central charge, which includes all inner charges of nucleus and inner electrons.
And "n" is the principal quantum number, which expresses major energy levels.
(Eq.3)
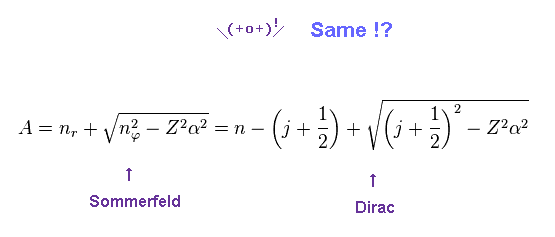
We replace a part of the denominator of Eq.2 by "A".
Of course, Sommerfeld and Dirac equations are the same.
(Eq.4) Conversion from Sommerfeld to Dirac forms.
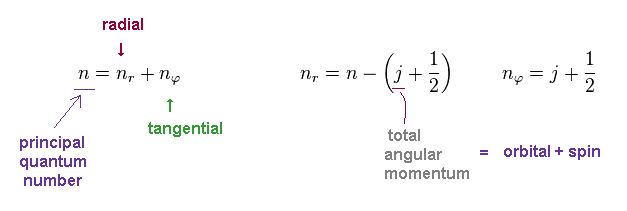
In Bohr-Sommerfeld model, the principal quantum number "n" is the sum of radial (= nr ) and tangential (= nφ ) quantum numbers.
In Dirac equation, they use the common variable "j" as total angular momentum.
This "j" is the sum of orbital (= "l") and spin (= s ) angular momentums.
So even if two states have different orbital angular momentum, their energy levels become the same, when their "j" are the common.
(Eq.5) Total energy.
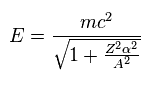
Using "A" of Eq.3, the energy level of Eq.2 can be expresses as Eq.5.
Here we apply Taylor expansion of Eq.6 to this equation.
(Eq.6) Taylor expansion.
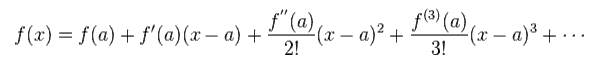
where
(Eq.7)
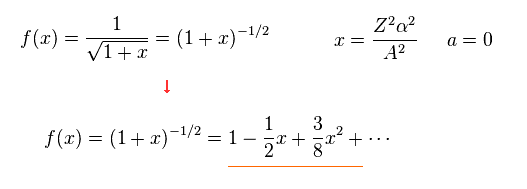
From Eq.7, total energy E of Eq.5 becomes
(Eq.8)
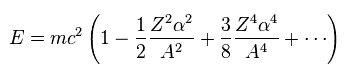
Using Eq.3 and approximation ( fine structure constant α is small ), we obtain.
(Eq.9)
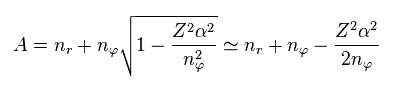
where we use
(Eq.10)
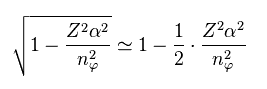
From Eq.9, we have
(Eq.11)
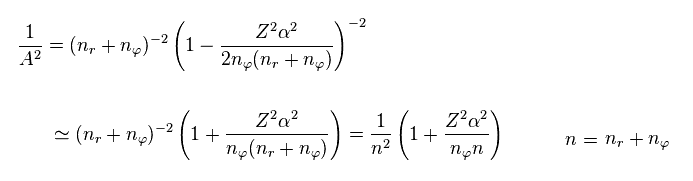
Furthermore, considering fine structure constant α is very small (= 1/137 ), we can use the following approximation.
(Eq.12)
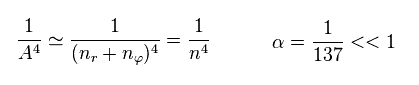
Substituting Eq.11 and Eq.12 into Eq.8, the total energy E becomes.
(Eq.13)
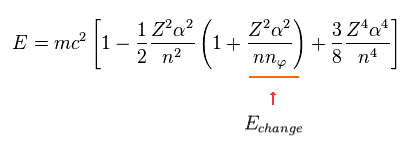
When the principal quantum number "n" is the common value, only angular number (= nφ ) influences the energy values.
So we pick up the term (= third term of Eq.13 ) including this nφ.
(Eq.14)
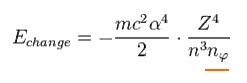
As you see Eq.14, this value is proportional to Z4/n3.
We want to calculate the energy difference between two states with angular momentum nφ and nφ+1 in the same "n".
(Eq.15)
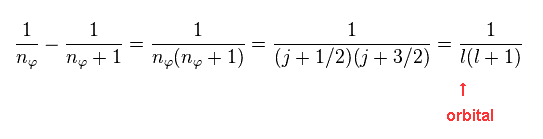
As shown in Eq.4, these two states correspond to two different "j" in Dirac form.
"l" is the orbital angular momentum.
(Eq.16) Energy difference (= fine structure ) between two states in the same "n".
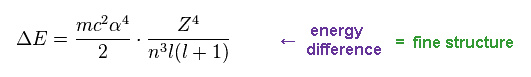
From Eq.14 and Eq.16, we find the energy difference between two states are proportional to Z4/n3.
These two states exist inside the same "n", and their "j" ( or nφ ) are different by one.

2014/8/15 updated. Feel free to link to this site.