Top page ( Quantum mechanics is false )
Strange "spin" is NOT a real thing
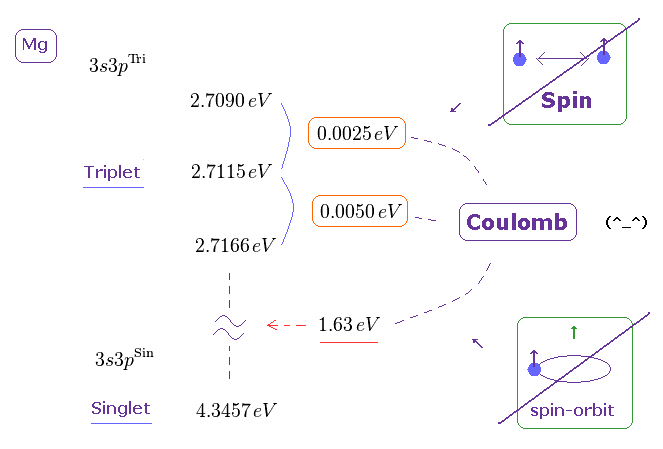
(Fig.1) Triplet, Singlet of Magnesium (= Mg ) mean large "Coulomb" energy ( NOT spin ).

Singlet-triplet energy levels' splitting in alkaline-earth metals such as magnesium, calcium is said to be caused by spin-spin interaction.
But in fact, the electron's spin-spin (magnetic) interaction or spin-orbit (effective) magnetic interaction are too weak to explain the singlet triplet energy splitting.
As shown in Nist, the magnesium singlet (= 3s3p 1p ) and triplet (= 3s3p 3p ) energy levels are in the upper figure, using unit conversion ( cm-1 → eV ).
The energy difference between singlet and triplet is ver big = 1.63 eV.
And the energy difference between three triplet states is about 0.0025 ~ 0.0050 eV, which is also too big to explain by tiny electron spin-spin magnetic interaction..
It is natural to think these singlet-triplet energy splitting is caused by Coulomb electric interaction related to inner electrons instead of fictional electron spin.
(Fig.2) Triplet state ? ← Only "Math", NOT physics.
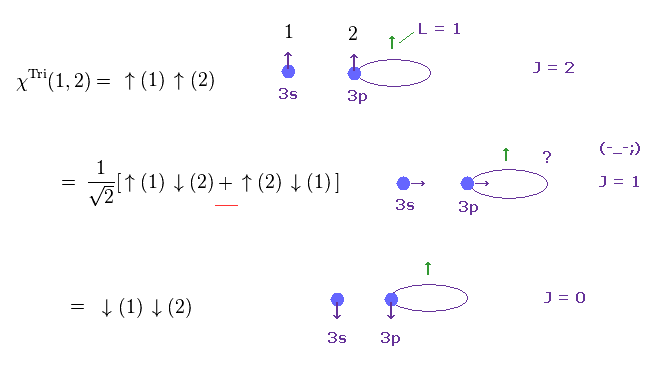
(Fig.3) Singlet state ? ← What is the physical meaning of ± sign ?

The singlet-triplet by electron spin is nonphysical.
As shown in the upper figure, both the singlet and triplet states include two electrons with up and down spins, and only the sign connecting ↑↓ ± ↓↑ is different, which states cannot be expressed by real things.
And it is unnatural that atomic energy levels of singlets have almost No link to triplet energy states.
(Eq.1) Conversion of energy units.
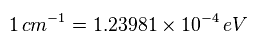
(Fig.4) Spin-spin magnetic dipole energy is too small to explain triplet splitting.
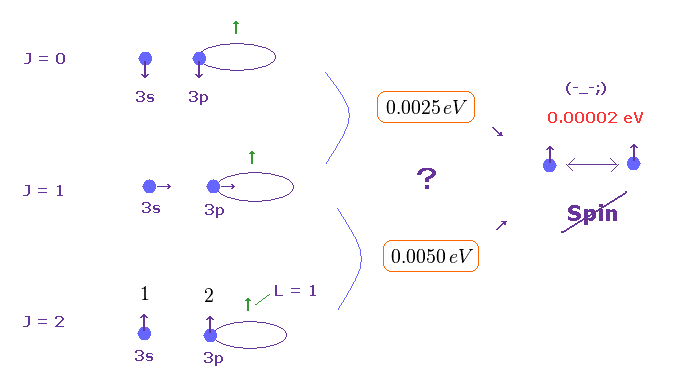
(Fig.5) Spin-spin magnetic energy (= only 0.00002 eV ) is too small to explain actual magnesium's triplet energy splitting (= 0.0050 eV ).
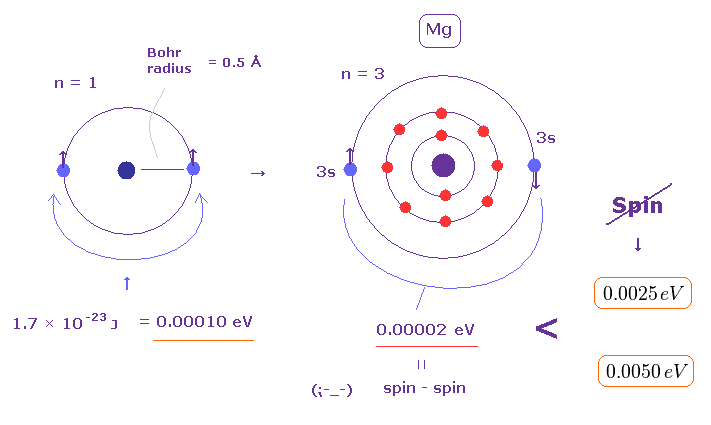
As shown on this and this-(33.9), electron spin-spin magnetic dipole energy is too weak (= less than 0.0001 eV ) to explain magnesium triplet energy splitting (= 0.005 eV ).
(Fig.6) Spin-orbit interaction (< 0.00034 eV ) is too small to explain triplet splitting (= 0.005 eV ).
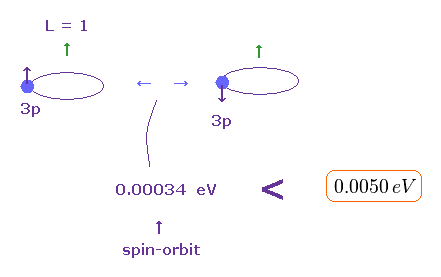
Relativistic spin-orbit magnetic interaction is also too weak to explain the magnesium triplet energy splitting.
(Fig.7) Both spin-spin and spin-orbit magnetic interactions are too small to explain triplet and singlet splitting that is caused by strong Coulomb interaction with inner electrons.
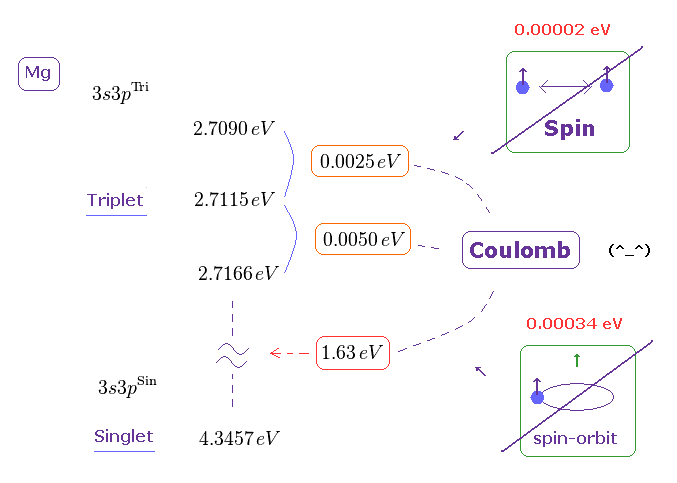
As a result, we find that these triplet and singlet energy splitting are caused by strong Coulomb interactions between inner electrons and valence electrons, neither by spin-spin nor spin-orbit coupling.
(Fig.8) Spin-spin magnetic dipole energy is too small ( < 0.0001 eV )
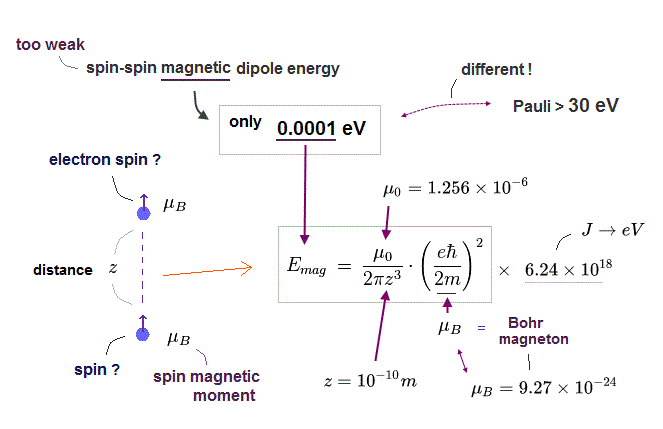
Here we calculate spin-spin magnetic dipole energy or interaction and show the spin magnetic interaction is too weak (= spin magnetic energy is too small ) to explain triplet energy splitting, strong Pauli exclusion repulsion and ferromagnetism, so electron spin is unreal.
When the distance between two electron spins (= spin magnet = Bohr magneton ) is "z ( or distance r apart )", its magnetic energy (= Emg ) becomes like Fig.8. See also this, this p.17, this, this-lower . Each spin magnetic moment is Bohr magneton (= μB )
Unrealistic electron spin is accidentally supposed to have the same magnetic moment = Bohr magneton as the Bohr's atomic orbit, as shown in this-lower.
Using these fundamental constants, you can calculate and estimate spin-spin magnetic dipole energy, which is far smaller (= about 0.0001 eV, when the distance between two spin magnetic moments is about 1 Å = 1 × 10-10 meter, this p.7-(12) ) than energies required to generate triplet splitting (= 0.005 eV ), strong Pauli exclusion repulsion (= about 30 eV ) or ferromagnetism (= 1 eV ), so electron spin is unreal.
(Fig.9) Spin-spin magnetic dipole energy. Part II.
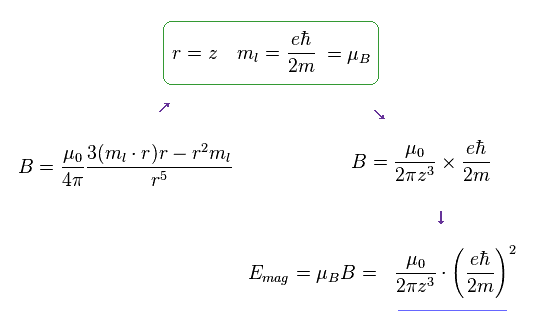
When the direction of "z" is different from spin, the generalized form of magnetic field (= B ) caused by spin becomes like Fig.9.
When "r" is (anti)parallel to ml (= magnetic moment ), this form is just equal to Fig.8.
So we use simple Fig.8 as spin-spin magnetic energy.
(Fig.10)
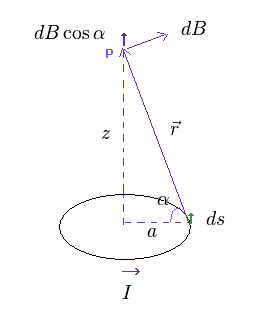
In Fig.10, the circular current I generates the magnetic field (= B ) at the point of "p".
Due to this circular elecric orbit, all magnetic fields other than z direction are cancelled out.
Only the z conponent (= dB cos α ) is left.
(Eq.2)
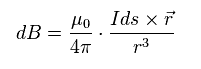
According to Biot-Savart law ( see this site ), magnetic field (= B ) is as shown in Eq.2.
"I" is electric current, "ds" is electric current fragment, and "r" is the distance between this fragment and the point "p".
(Eq.3)
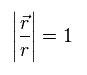
In Eq.2, the unit vector in "r" direction is Eq.3.
Using Eq.3 in Eq.2, the z component of total magnetic field becomes
(Eq.4)
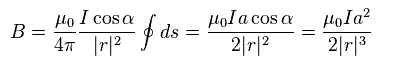
where
(Eq.5)
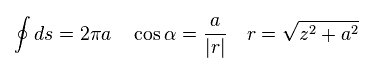
The result of Eq.4 is the same as this site.
Using Eq.5 and the definition of Iπa2 = magnetic moment (= Bohr magneton ), Eq.4 becomes Eq.6.
( About elliptical orbit, see this section. )
(Eq.6) magnetic field B caused by one spin magnet with Bohr magnetoton
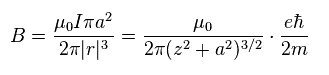
The magnetic energy (= Emg ) is given by magnetic moment (= μB ) × B.
(Eq.7) Spin-Spin magnetic energy.
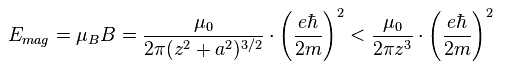
If the circular current is spin, the orbital radius "a" is almost zero in Eq.7 right ( a → 0 ).
( Of course, when this "a" is not zero, this magnetic energy becomes smaller, as shown in Eq.7. )
Eq.7 result is the same as this site (33.9).
If we can know the distance (= z ) between two spins in outer orbitals of magnesium, the magnetic energy of Eq.7 is determined.
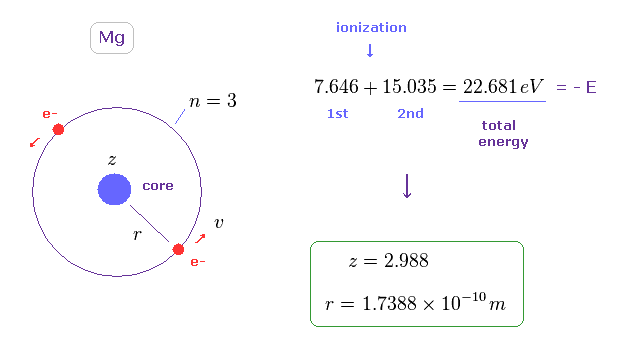
(Fig.11) Estimated radius of 3s orbital in Mg.
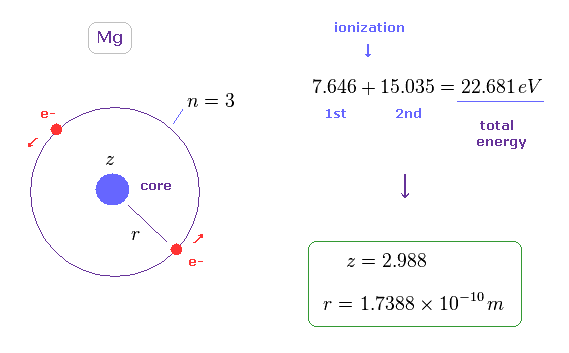
To know the average distance between two spins in outer orbitals of Mg, we use the simple model of Fig.11.
In Fig.11, two ( outer ) electrons are on the opposite sides of the core (= effective positive charge "z" ), and moving on the same orbit (= 3 × de Broglie wavelength ).
We use the sum of the 1st and 2nd ionization energies ( 7.646 + 15.035 =
Using this total energy, we obtain the radius of r = 1.7388 Å, and the central effective charge z = 2.988.
This radius is almost same as this site.
About the detailed calculation, see this section.
(Eq.8) Radius of hydrogen-like atom.
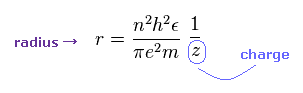
The orbital radius is proportional to a square of principal number (= n2 ), and in inverse proportion to the central charge (= z ).
(Fig.12) Rough estimation of radius of Mg 3s orbital ( z = 3 ).
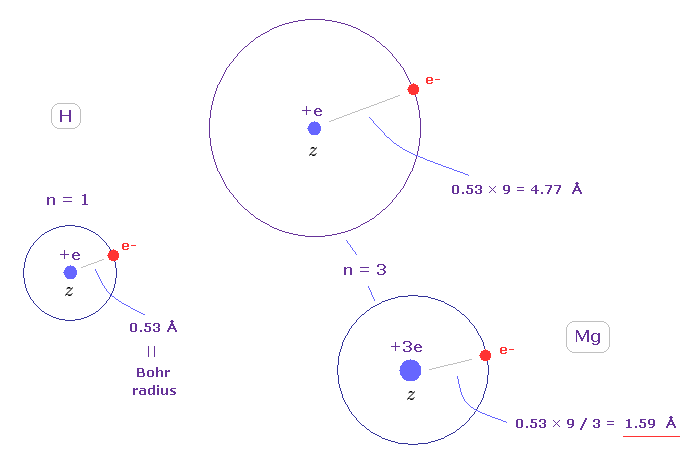
The atomic radius of the ground state hydrogen ( z = 1, n = 1 ) is just Bohr radius (= 0.53 Å ).
So the orbital length of n = 3 is 9 × 0.53 = 4.77 Å.
Suppose the central charge of Mg2+ is about z = 3 ( this z becomes a little bigger than "2" due to "gap" of inner orbitals ).
This Mg radius becomes 0.53 × 9 / 3 = 1.59 Å, which is similar to the result of 1.738 Å of Fig.11.
( Considering the repulsive effect of another outer electron, the actual effective charge becomes less than "3". )
(Fig.13)
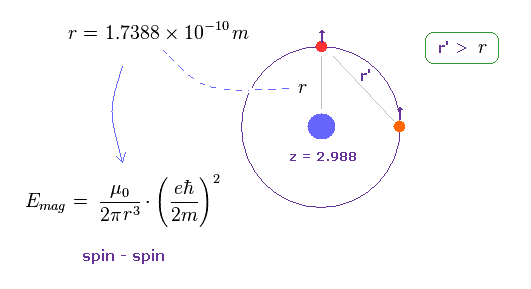
"r" of Fig.11 is radius of outer orbital of Mg.
So the distance (= r' ) between two valence electrons is longer than this radius, as shown in Fig.13 ( r' > r ).
Sspin-spin magnetic energy is given by this and the estimated magnesium radius (= 1.7388 Å )
(Eq.8) Magnesium's estimated spin-spin magnetic energy is too small (= only 2.042 × 10-5 eV )
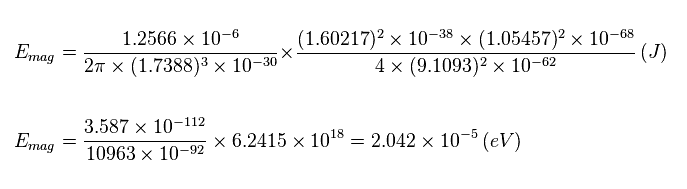
So, the spin-spin magnetic dipole energy is less than 2.042 × 10-5 eV.
This value is very small, which is about 1/100 times the actual triplet splitting (= 0.0025 or 0.0050 eV, see Fig.1 ).
(Fig.14) Spin-Spin magnetic energy is too small (= 2.042 × 10-5 eV = 0.00002 eV ) to explain magnesium triplet energy splitting (= 0.005 eV ).
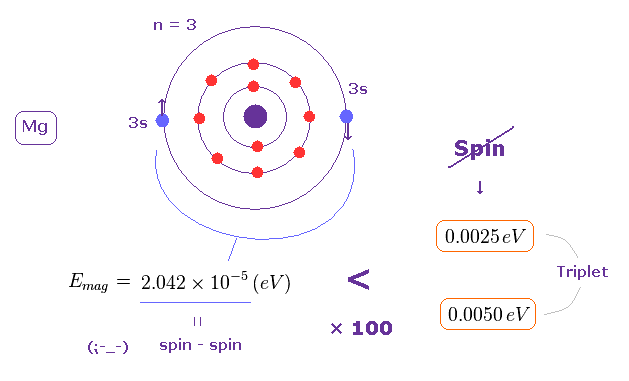
You can easily understand it is impossible to explain triplet splitting using spin-spin magnetic interaction.
In spite of this fact, they never give up this strange "spin".
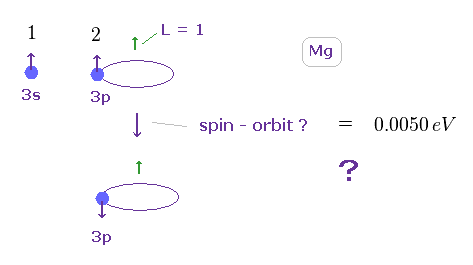
(Fig.15) Spin-orbt magnetic coupling is too small to explain the magnesium's triplet energy splitting (= 0.005 eV ).
(Fig.16) Doublet of hydrogen (= H ) and triplet of magnesium (= Mg ).
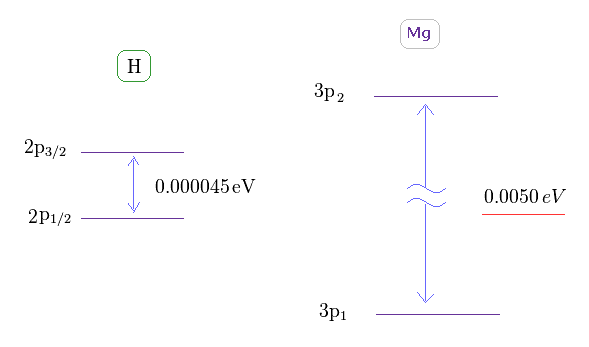
As shown on this site ( or Nist ), hydrogen fine structure (= doublet ) between 2p3/2 and 2p1/2 is about 0.000045 eV.
On the other hand, triplet energy splitting of magnesium is as large as 0.0050 eV. See Nist and use this.
According to the current quantum mechanics, triplet splitting must be caused by change of spin directions in 3s-3p orbitals.
But actually, neither spin-spin nor spin-orbit magnetic energy can explain this triplet energy splitting.
(Fig.17) Core charge of magnesium is much bigger then Z = 2 !?
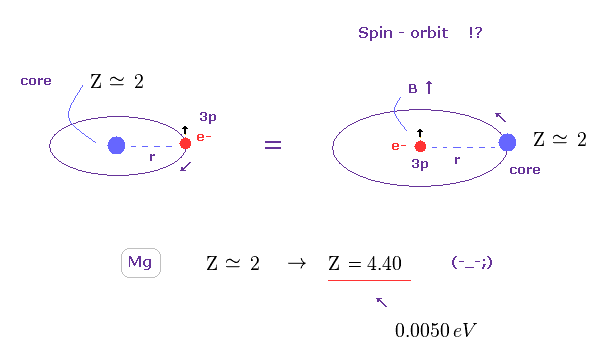
The magnesium has two valence electrons ( in this case, one is 3s, and another is excited to 3p ).
So the Ma2+ ion has about Z = +2 central core charge.
From the viewpoint of 3p electron, core charge Z is moving around 3p electron, and generates magnetic field (= B ), which is the origin of spin-orbit magnetic energy according to the paradoxical Einstein relativistic theory.
But if you try to get triplet energy splitting (= 0.0050 eV ) using relativistic spin-orbit magnetic energy, this central core charge becomes unrealistically as big as Z = 4.40.
This result clearly shows spin-orbit coupling has nothing to do with Mg triplet ( of course, singlet ).
(Fig.18) Energy splitting (= ΔE ) by spin-orbit interaction.
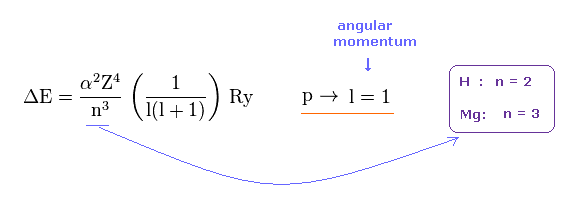
It is known that energy splitting by spin-orbit coupling is proportional to Z4 ( Z is central charge ), and in inverse proportion to n3 ( n is principal quantum number ), as shown on this p.9-(1.37), this p.9-(5.32), this p.3-left-1st-paragraph, this p.9-lower.
↑ Angular momentum quantum number L or l (= ell ) is equal to ( L = 1 ) in all atomic p states, so we need to focus only on Z and n to compare relativistic spin-orbit magnetic energies between different atoms.
Hydrogen doublet is n = 2 energy level. Magnesium in this case is n = 3 energy level.
Angular momentums of "p" orbital are the same in both atoms ( l = 1 in H and Mg ).
(Fig.19) How big is central core charge Z in Mg ?
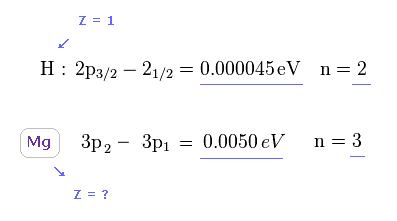
As a result, the central core charge Z of Mg must be much bigger than H to explain large discrepancy between this energy splitting of Mg and H.
( Of course, central charge of H is Z = 1 ).
(Fig.20) Effective core charge of Mg becomes as large as Z = 4.40 !?
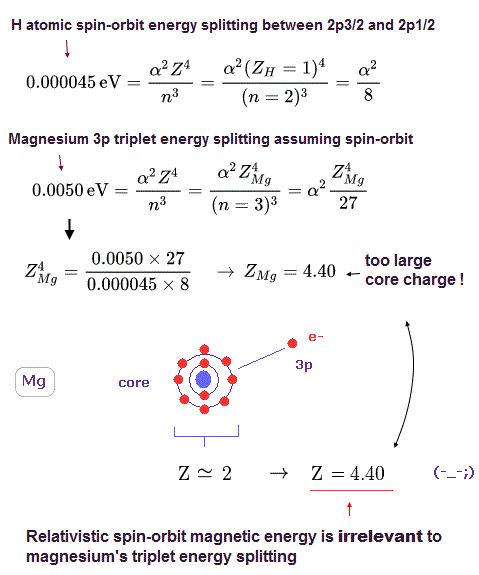
Using Fig.18 and Fig.19 ( comparing the values of H and Mg ), we can know the central core charge Z of Mg.
As shown in Fig.20, this charge of Mg becomes as large as Z = 4.40 !
Of course, this central core charge Z = 4.40 is too big and unrealistic.
This calculation result clearly proves spin-orbit coupling has nothing to do with Mg triplet enegy splitting, because it's too weak.
(Fig.21) What is effective core charge Z in Mg ?
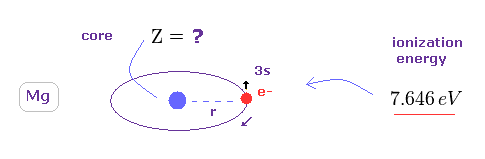
We can know true effective core charge Z based on ionization energy of Mg.
The first ionization energy of Mg is 7.646 eV.
( This electron is "3s". Of course, "3p" electron is farther away from nucleus, so Z becomes smaller. )
(Fig.22)
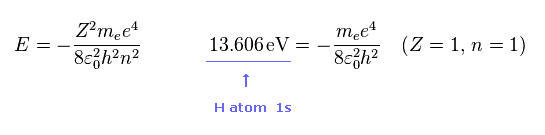
As you know, hydrogen ionization energy of 1s electron is 13.606 eV.
In 1s hydrogen, Z = 1 and n = 1.
(Fig.23) What is effective core charge Z in Mg ?
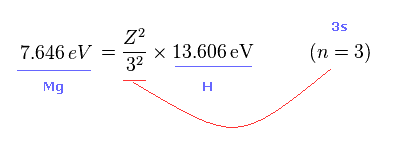
From Fig.21 and Fig.22 we get the relation of Fig.23.
Z of Fig.23 means effective core charge from the viewpoint of Mg 3s electron.
( Caution: this Z contains Mg nucleus and all electrons including another 3s electron except one outmost 3p electron. )
(Fig.24) Effective core charge Z in Mg.
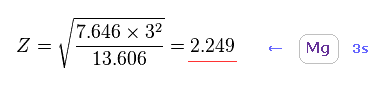
Solving Fig.23, we get the true effective core charge Z = 2.249 based on the experimental magnesium's ionization energy.
(Fig.25) Wide discrepancy between true and "fake" core charges.
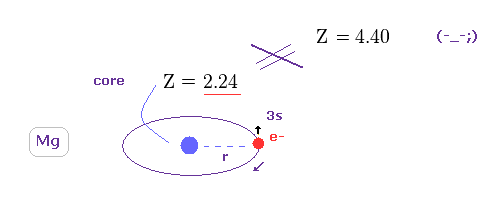
Comparing Fig.24 ( true Z = 2.24 ) and Fig.20 ( Z = 4.40 by spin-orbit ), you can easily find that spin-orbit coupling is too weak to explain Mg triplet (= so the too weak relativistic spin-orbit magnetic interaction needs unrealistically-large fictional core charge Z = 4.40 ).
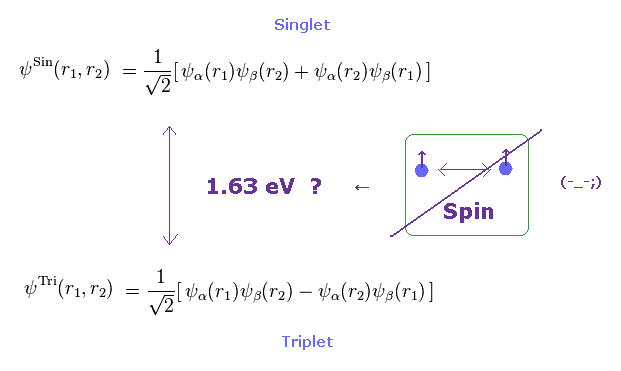
(Fig.26) Triplet, Singlet of Mg have Nothing to do with "Spin" .

Using true effective core charge (= Z = 2.24 instead of the too large Z = 4.40 ), the relativistic spin-orbit magnetic coupling energy becomes as small as 0.00034 eV (= far smaller than the magnesium's triplet energy splitting of 0.005 eV ).
As you see Fig.26, the energy difference between singlet and triplet is much bigger (= 1.63 eV ).
So it is much more impossible to insist this wide energy gap is caused by very weak spin.
They insist this large enery gap (= 1.63 eV ) is due to the difference of (nonphysical) symmetric and antisymmetric wavefunction, as shown in Fig.31.
(Fig.27) "Symmetric" and "antisymmetric" wavefunctions can cause large energy gap ?
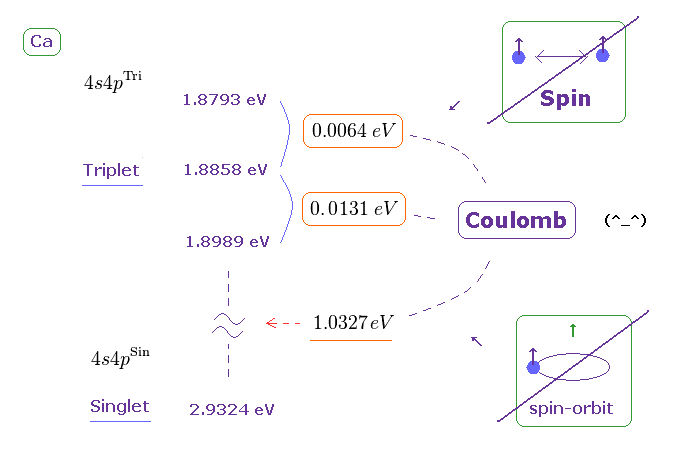
(Fig.28) Triplet, Singlet splitting in Ca is too large for spin-spin (-orbit) coupling.
Triplet and singlet energy levels are on this site.
Converting energy unit ( cm-1 → eV ) by
(Eq.9)
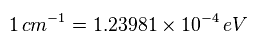
We obtain Fig.28.
If you compare Fig.28 (= Ca ) with Fig.26 (= Mg ), you will understand energy splitting (in triplet ) in Ca is larger than Mg.
So it is much more impossible that spin-spin ( or -orbit ) coupling is involved in this triplet.
(Fig.29) Estimated radius of Ca from ionization energy.
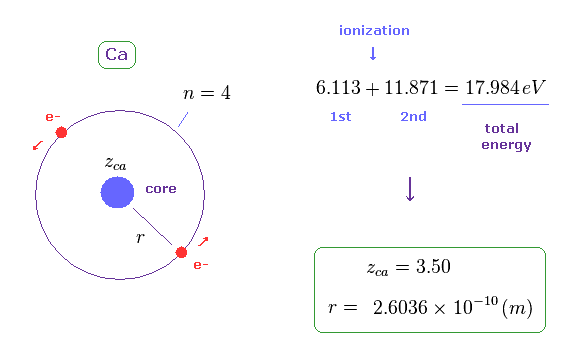
The sum of 1st and 2nd ionization energy of Ca is 17.984 eV, as shown on this site.
Like Fig.11, we suppose helium-like model in Ca, and its total energy is -17.984 eV.
In this model, the radius (= r ) becomes 2.6036 Å, which is longer than Mg.
The calculation method is the same as this section.
(Fig.30) Spin-spin magnetic energy is 1/1000 times triplet splitting in Ca.
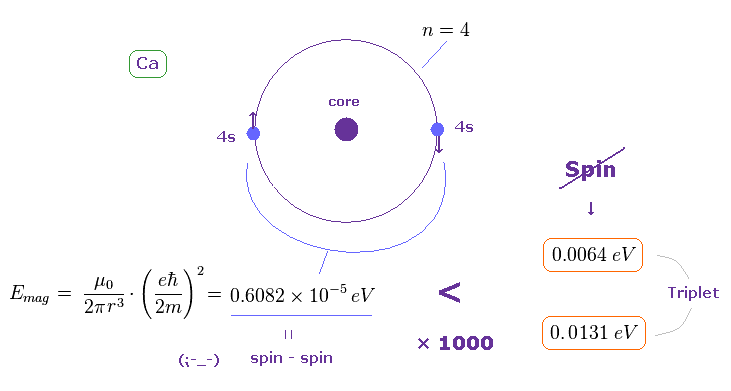
Using the approximate radius of Fig.29, we find the spin-spin magnetic dipole energy in Ca outer orbital becomes very small.
(= 0.6082 × 10-5 eV, about the method, see this )
This result shows it is impossible to explain triplet splitting (= 0.0131 eV in Ca ) by the tyny spin-spin magnetic interactions (= 0.000006082 eV ) also in calcium.
(Fig.31) Doublet of H 2p and triplet of Ca 4p.
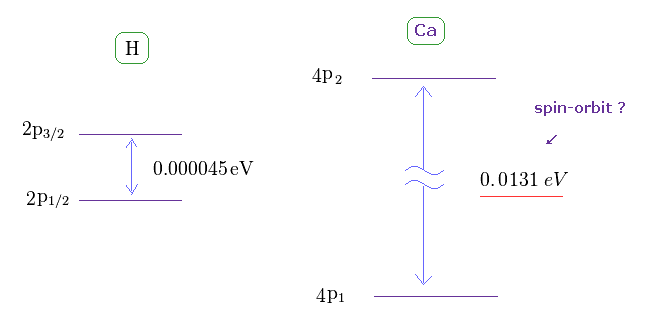
The triplet energy intervals of Ca is much larger than hydrogen 2p doublet.
As I said above, spin-spin interaction has NO relation with this triplet.
So there is ONLY spin-orbit coupling left, if "spin" is involved in this triplet.
(Fig.32) Effective core charge Z becomes unrealistically too large. ( Z = 2 → 6.946. )
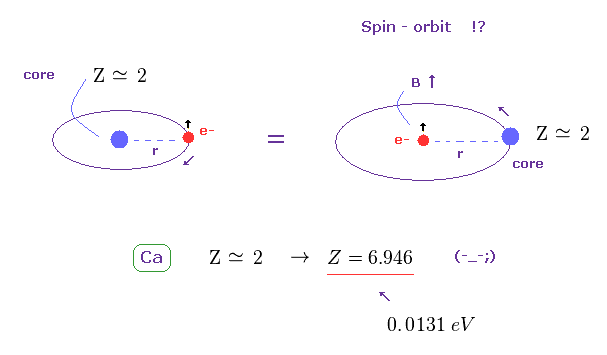
Like in this section, we suppose triplet of Ca is due to spin-orbit coupling (= relativistic spin-orbit magnetic energy ), and calculate effective core charge Z (= total charge containing Ca nuclear and all innter electrons except one outer 4p electron ).
If so, this charge Z becomes unrealistically too big ( Z = 6.946 ) to explain large energy interval of 0.0131 eV.
As a result, spin-orbit coupling proves to be NOT involved in this triplet, either.
(Fig.33) True effective charge Z = 2.68.
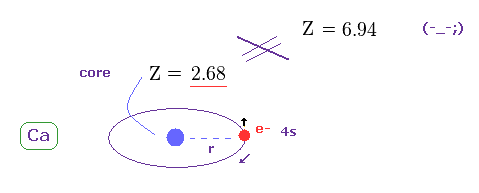
Using the first ionization energy of 6.113 eV, we can know the true effective core charge Z, like in this section.
This true effective charge (= 2.68 ) based on ionization energy is much smaller than Z = 6.94.
Again, spin-orbit coupling proves to have NO relation with triplet splitting.
(Fig.34) Triplet, Singlet splitting in Sr is too large for spin-spin (-orbit) coupling.
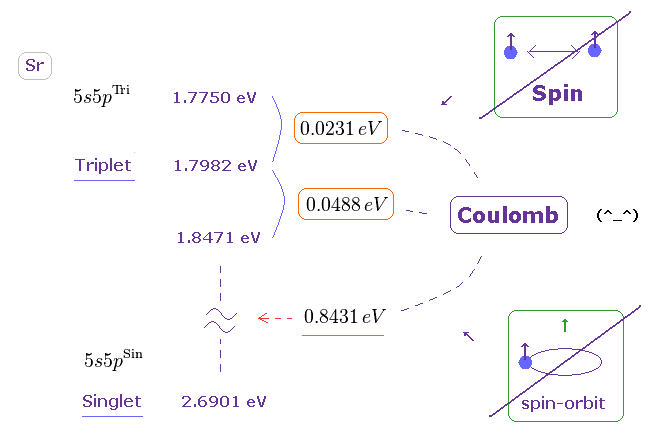
Triplet and singlet energy levels of Sr are shown on this site.
Converting energy unit ( cm-1 → eV ) by
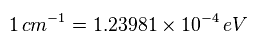
We obtain Fig.34.
If you compare Fig.34 (= Sr ) with Fig.26 (= Mg ), you will understand energy splitting (in triplet ) in Sr is much larger than Mg.
So it is much more impossible that spin-spin ( or -orbit ) coupling is involved in this triplet.
(Fig.35) Radius of helium-like model in Sr.
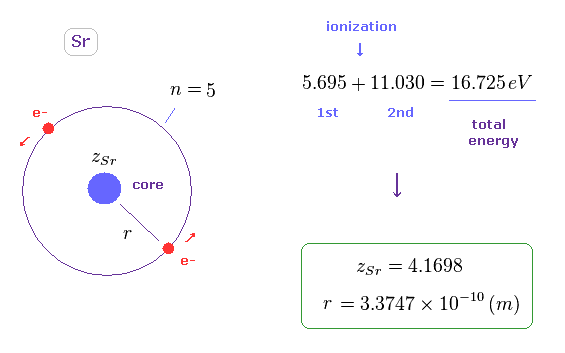
The sum of 1st and 2nd ionization energy is 16.725 eV in Sr, as shown on this site.
Like Fig.11, we suppose helium-like model in Sr, and its total energy is -16.725 eV.
In this model, the radius (= r ) becomes 3.3747 Å, which is longer than Mg.
(Fig.36) Spin-spin magnetic energy is 1/10000 times triplet splitting in Sr.
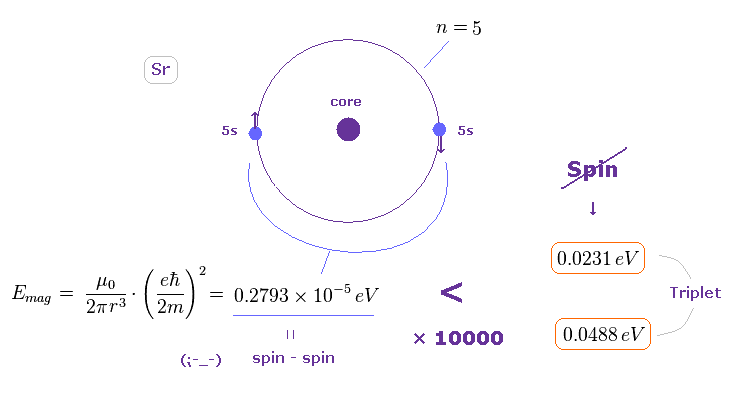
Using the approximate radius of Fig.35, we find the spin-spin magnetic dipole energy in Sr outer orbital becomes very small.
(= 0.2793 × 10-5 eV, about the method, see this section. )
This result shows it is impossible to explain triplet splitting by spin-spin magnetic interactions also in Sr.
(Fig.37) Doublet of H 2p and triplet of Sr 5p.
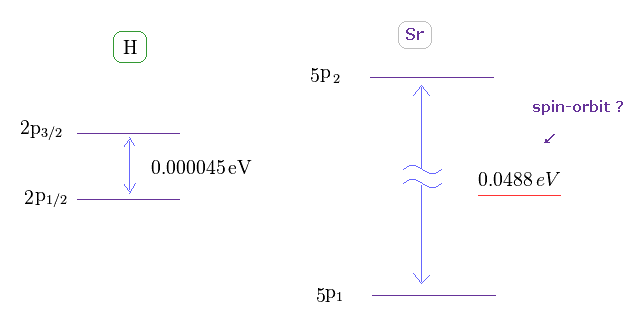
The triplet energy intervals of Sr is much larger than hydrogen 2p doublet.
As I said above, spin-spin interaction has NO relation with this triplet.
So there is ONLY spin-orbit coupling left, if "spin" is involved in this triplet.
(Fig.38) Effective core charge Z becomes unrealistically too large. ( Z = 2 → 11.409 )
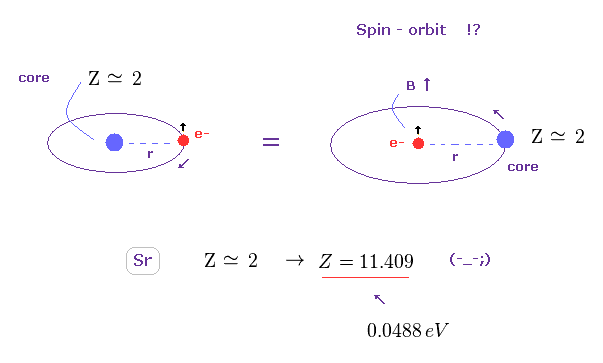
Like in this section, we suppose triplet of Sr is due to spin-orbit coupling, and calculate effective core charge Z.
If so, this charge Z becomes unrealistically too big ( Z = 11.409 ) to explain large energy interval of 0.0488 eV.
As a result, spin-orbit coupling proves to be NOT involved in this triplet, either.
(Fig.39) True effective charge Z = 3.23.
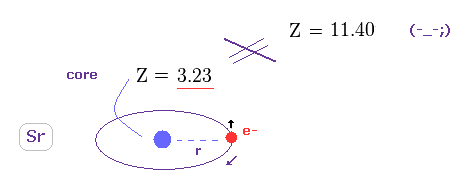
Using the first ionization energy of 5.695 eV, we can know the true effective core charge Z, like in this section.
This true effective charge (= 3.23 ) based on ionization energy is much smaller than Z = 11.409.
Again, spin-orbit coupling proves to have NO relation with triplet splitting.
(Fig.40) Triplet, Singlet splitting in Ba is too large for spin-spin (-orbit) coupling.
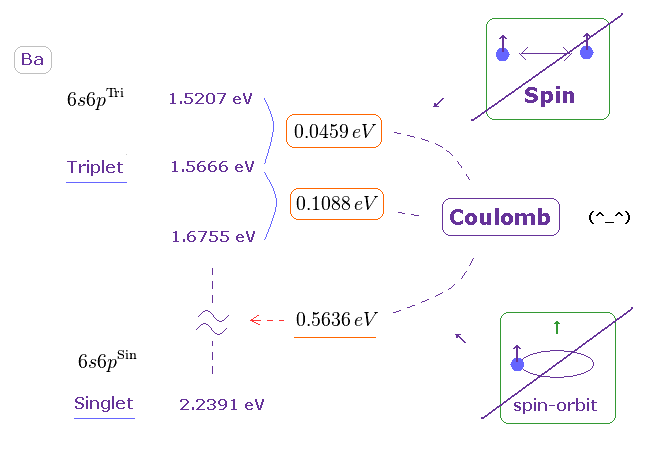
Triplet and singlet energy levels are shown on this site.
Converting energy unit ( cm-1 → eV ) by
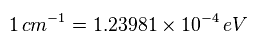
We obtain Fig.40.
If you compare Fig.40 (= Ba ) with Fig.26 (= Mg ), you will understand energy splitting (in triplet ) in Ba is much larger than Mg.
So it is much more impossible that spin-spin ( or -orbit ) coupling is involved in this triplet.
(Fig.41) Estimated radius of Ba.
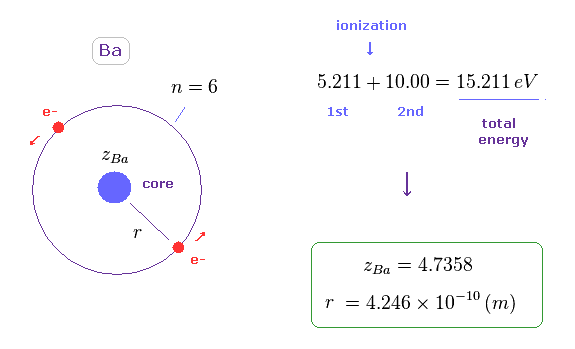
The sum of 1st and 2nd ionization energy is 15.211 eV in Ba, as shown on this site.
Like Fig.11, we suppose helium-like model in Ba, and its total energy is -15.211 eV.
In this model, the radius (= r ) becomes 4.246 Å, which is longer than Mg.
The calculation method is the same as this section.
(Fig.42) Spin-spin magnetic energy is 1/10000 times triplet splitting in Ba.
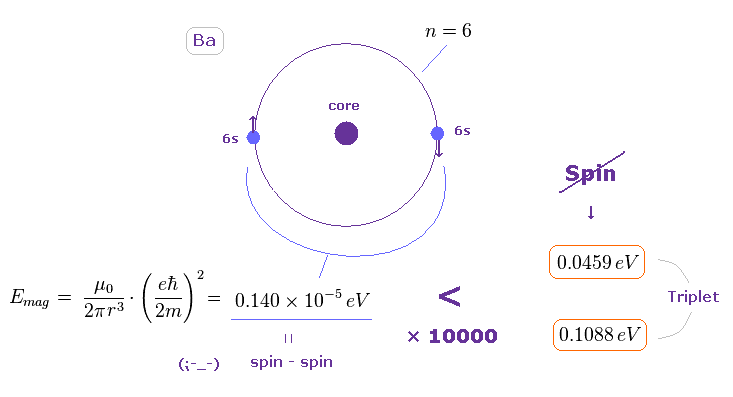
Using the approximate radius of Fig.41, we find the spin-spin magnetic dipole energy in Ba outer orbital becomes very small.
(= 0.140 × 10-5 eV )
This result shows it is impossible to explain triplet splitting by spin-spin magnetic interactions also in Ba.
(Fig.43) Doublet of H 2p and triplet of Ba 6p.
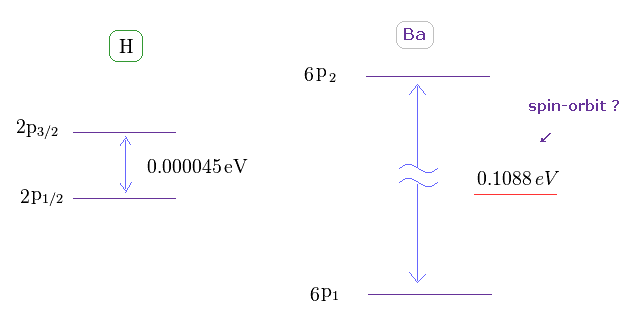
The triplet energy intervals of Ba is much larger than hydrogen 2p doublet.
As I said above, spin-spin interaction has NO relation with this triplet.
So there is ONLY spin-orbit coupling left, if "spin" is involved in this triplet.
(Fig.44) Effective core charge Z becomes unrealistically too large. ( Z = 2 → 15.984 )
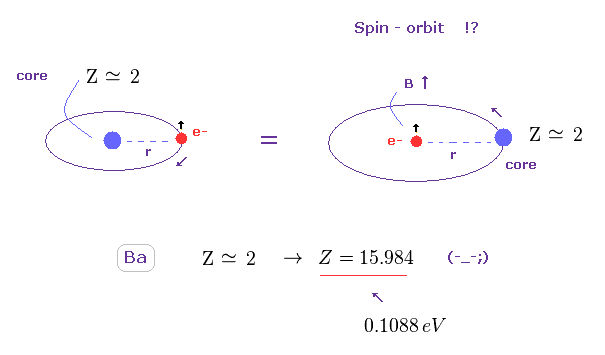
Like in this section, we suppose triplet of Ba is due to spin-orbit coupling, and calculate effective core charge Z.
If so, this charge Z becomes unrealistically too big ( Z = 15.984 ) to explain large energy interval of 0.1088 eV.
As a result, spin-orbit coupling proves to be NOT involved in this triplet, either.
(Fig.45) True effective charge Z = 3.71.
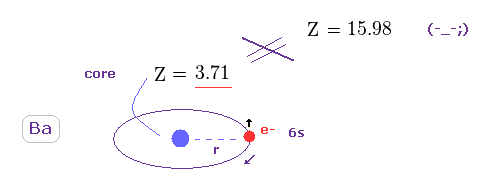
Using the first ionization energy of 5.211 eV, we can know the true effective core charge Z, like in this section.
This true effective charge (= 3.71 ) based on ionization energy is much smaller than Z = 15.984.
Again, spin-orbit coupling proves to have NO relation with triplet spilitting in Ba.
(Fig.50) Energy levels of Calcium (= Ca ).
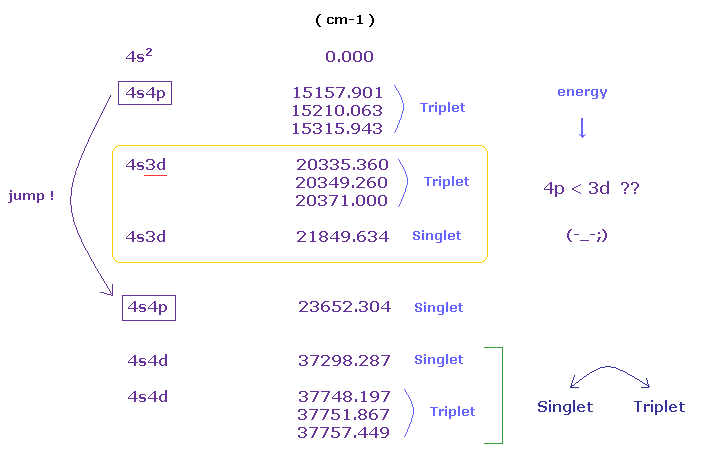
If you see the energy levels of Ca (= Nist ) carefully, you will find quantum numbers and their orders are very unreasonable.
In usual periodic table, "3d" orbitals are lower than 4p orbitals in the energy levels.
But as you see Fig.50, 4p orbital (= triplet ) is lower than 3d orbitals.
( In Fig.50, the top (= 4s2 ) is ground state, and the lower configuration means higher energy levels. )
And in 4s4d configuration, the order of triplet and singlet is reversed.
( Usually, triplet → singlet. But in 4s4d, singlet → triplet. )
(Fig.51) Energy levels of Mg and Sr. "4f" appears ONLY in Mg ?
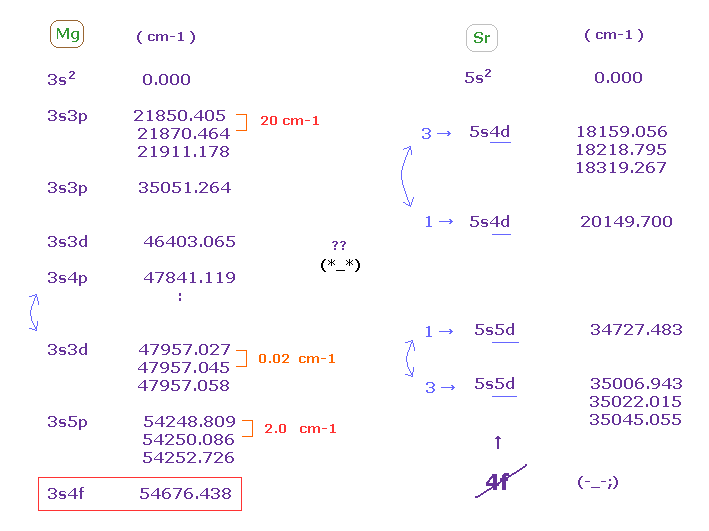
In magnesium, the energy intervals of triplets are chaotic.
( 3s3p-- 20 cm-1, 3s3d-- 0.02 cm-1, 3s5p-- 2.0 cm-1 ).
And "4f" energy levels exist only in magnesium, but don't exist in strontium and barium .
This is strange.
Though "3d" orbital is lower than "4p" in energy levels, but in Mg, "3s4p" becomes lower than "3s3d".
This is strange, too.
In Sr, "triplet" (= 3 ) appears first in 5s4d, but "singlet" (= 1 ) appears first in 5s5d.
Again, this is one of artificial manipulations.
So the concepts of these triplet and singlet were produced by considering ONLY unrealistic quantum numbers.
They completely ignored the magnitude of energy ( ← though very important ! ) and their orders.
(Sp.1)
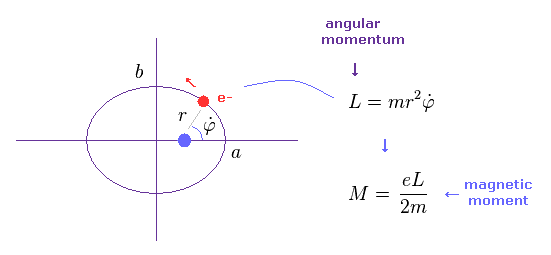
In the upper section, we deal with simple circular orbit.
In this section, we show the magnetic moment of elliptical orbit becomes the same as circular orbit like Sp.1
(Sp.2)
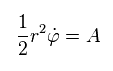
In the system of central force, the areal velocity (= A ) is constant like Sp.2.
(Sp.3)
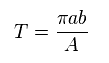
The total area of ellipse is equal to "πab".
Time period (= T ) of one-orbit is given by the total area (= πab ) / A.
Using Sp.2 and Sp.3, the current I becomes
(Sp.4)
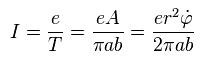
The magnetic moment (= M ) is given by the current I × area.
( When you divide some area into infinitesimal loops, you will find this law holds in any forms of current. )
As a result,
(Sp.5)
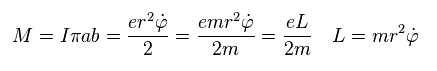
"3p" orbital has the angular momentum of 1 × ħ.
Substituting ħ into Sp.5, we obtain the Bohr magneton as the orbital magnetic moment of "3p".
(Sp.6) 3p = Bohr magneton.
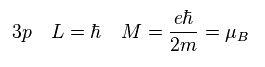
(Sp.7) 3s outer orbitals of Magnesium.
In Sp.7 magnesium model, two 3s outer electrons are moving on the common orbit at the velocity "v", on the opposite sides of the nucleus.
The effective positive charge of the core (= Mg nucleus + all inner electrons ) is "z".
And the orbital radius is "r".
Equating the centrifugal force to the Coulomb force, we have
(Sp.8)
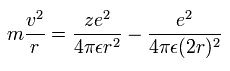
where "m" is the electron mass.
The left side is centrifugal force, and the first term of the right side is Coulomb attractive force between the core and each electron.
The second term is the repulsive force between two electrons.
The circular orbital length is supposed to be an integer (n) times de Broglie wavelength ( λ = h/mv ) of the electron.
(Sp.9)
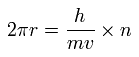
The total energy E is the sum of the kinetic and the Coulomb potential energy of the two electrons, so
(Sp.10)
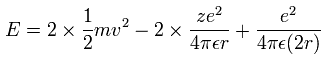
Suppose the total energy E of Sp.10 is equal to the sum of 1st and 2nd ionization energies ( E = -22.681 eV ).
Solving the the simultaneous equations of Sp.8-Sp.10, we can obtain the radius "r" and effective charge "z".
From Sp.9,
(Sp.11)
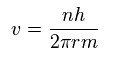
Substituting Sp.11 into Sp.8, we have
(Sp.12)
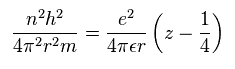
From Sp.12
(Sp.13)
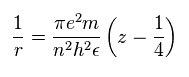
Substituting Sp.11 and Sp.13 into Sp.10,
(Sp.14)
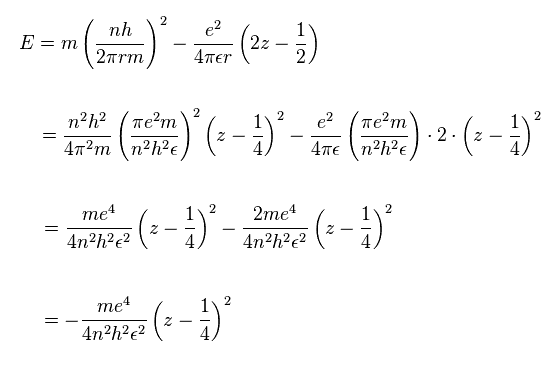
Here we treat Mg with two valence electrons as helium-like atom.
The total energy of these two outer electrons is supposed to be the sum of 1st and 2nd ionization energies ( see this site ) like Sp.15.
(Sp.15)

Substituting Sp.15 ( "eV" → "J" ) and n = 3 into Sp.14,
(Sp.16)
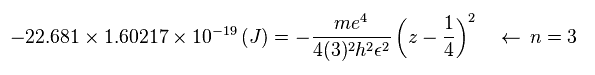
Using the following values,
(Sp.17)
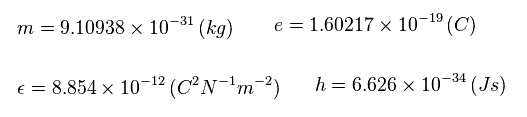
The central effective charge z becomes
(Sp.18)
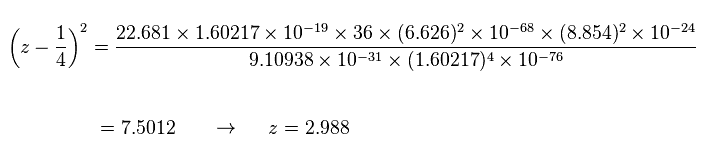
Substituting z = 2.988 and n = 3 into Sp.13, the radius "r" becomes
(Sp.19)
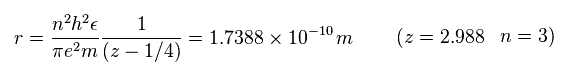

2014/2/21 updated. Feel free to link to this site.