Top page (correct Bohr model including the two-electron atoms)
Electron spin is an illusion !.
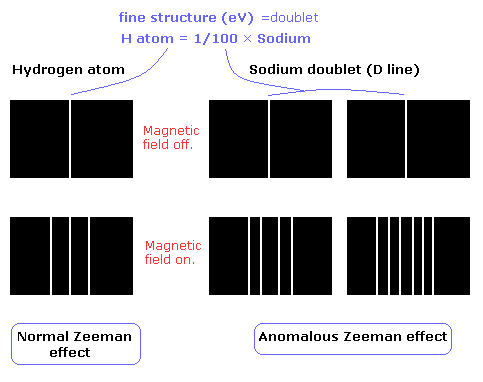
The Zeeman effect of the hydrogen atom shows the expected equally-spaced triplet (= "normal" Zeeman effect).
On the other hand, the sodium D lines (D1 and D2 doulet) show "anomalous" Zeeman effect ( due to the many inner electrons).
( Fig. 1 )

The fine structure of the hydrogen atom is very small (about 0.00005 eV), which is 1/100 of that of the sodium.
So under the normal magnetic field (about 1T), we can not confirm the Lande g factor (=anomalous Zeeman effect) in the hydrogen atom.
Of course, Bohr sommerfeld model can explain the fine structure correctly, though it has no electron spin. (See this page !)
Even if we use Bohr model, we can explain the even-numbered splitted lines (=doublet).
It is said that the normal Zeeman effect is observed in the spin zero states.
But also in the normal Zeeman effect, we can not neglect the electron spin (in the quantum mechanics).
Because the electron spin has as large magnetic moment (= Bohr magneton ) as that of the ħ × orbital motion.
(As a result, the magnetic moments (= Bohr magneton ) of the hydrogen ground state electron are the same in Bohr model and the quantum mechanical model. )
So to be precise, the normal Zeeman effect of the hydrogen atom in Fig.1 is "Paschen - Back effect" (Fig.2 and 3).
In the Paschen-Back effect, when the external magnetic field is stronger than the fine structure's level (= spin-orbital interaction level), the orbital and spin angular momenta become "quantized" in the direction of the magnetic field (B) (See Fig.2).
As the spin g factor (=2) is twice the orbital g-factor (=1), the energy difference under the magnetic field (B) is "Bohr magneton × B" in both of them (due to 2 × 1/2 = 1 × 1).
( Fig. 2 ) Paschen-Back effect of the hydrogen atom. = Normal Zeeman effect.
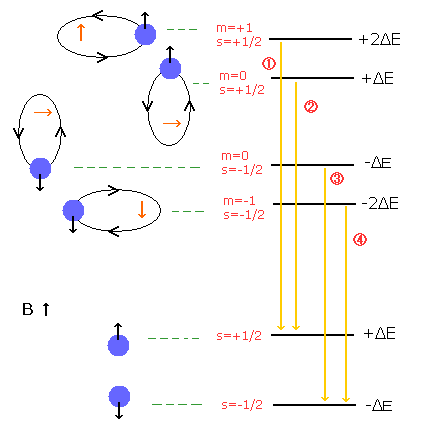
( Fig. 3 ) Paschen-Back effect also shows the equally-splitted triplet lines.
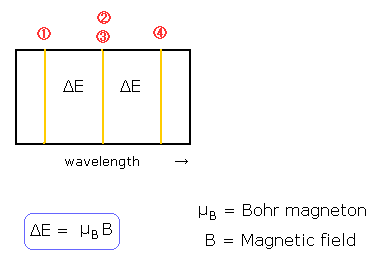
The quantization of the orbital angular momentum in Fig.2 is strange, I think.
Basically, the N pole is attracted to the S pole (S is attracted to N pole) in the external megnetic field.
Or according to the Lorentz force, the direction of angular momentum becomes parallel to the magnetic field.
(Caution: those two effects are opposite, because the Lorentz force causes the dipole to cancel the external magnetic field.)
So the external magnetic field forces the dipoles of the electron magnetic moment to line up in parallel to the external magnetic field.
This means that the electron's orbital plane is "naturally" perpendicular to the external magnetic field.
But in the state of m=0 in Fig.2, the magnetic moment caused by the electron's orbital motion is perpendicular to the external magnetic field !
It is unstable and very unnatural !
On the other hand, Bohr-Sommerfeld model can explain the equally-splitted triplet lines (= normal Zeeman effect), even if it doesn't use the "unnatural" m=0 angular momentum states (Fig.4).
( Fig. 4 ) Paschen-Back effect in the Bohr-Sommerfeld model.
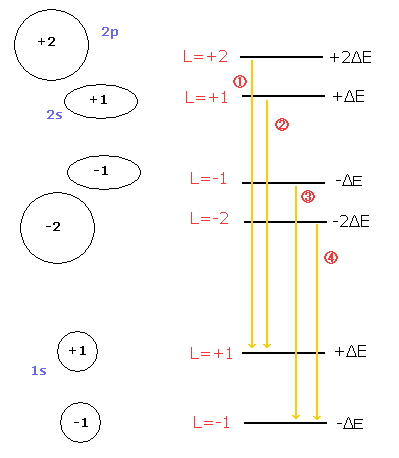
If the external magnetic field is so weak that the relativistic mass difference between 2s and 2p influences the splitted lines, Bohr sommerfeld model can show the even-numbered splitted lines, too.
As the electron speed of 1s state is faster than that of 2s state, the Lorentz force by the magnetic field is stronger in the 1s state.
(Of course, the relativistc effect is stronger in the 1s state than the 2s.)
+1 and -1 of the 1s state in Fig.4 receive the "opposite directioned" magnetic forces (outward or inward).
The relativistic mass changes become different in +1 and -1 of the 1s state.
As a result, the lines 2 and 3 of Fig.4 become separated, which gives "even-numbered" splitted lines.
But it is impossible that we can confirm the anomalous Zeeman effect correctly in the hydrogen atom like the sodium.
Because the energy difference of the fine structure in the hydrogen atom is about 1/100 of that of the sodium.
(We can not observe many lines in the hydrogen atom like the sodium of Fig.1.)
The Bohr Sommerfeld model of Fig.4 doesn't contain the "unnatural" m=0 state.
(This is why Bohr model can explain the Stern-Gerlach experiment in which the atoms are splitted into two.)
Of course, it is possible that the electron's magnetic moment is not completely parallel to the magnetic field also in the Bohr Sommerfeld model, when the external magnetic field is very weak. (In this case, it precesses.)
But in the quantum mechanical model, even if the external magnetic field is very strong, it always contains the "unnatural" m=0 state !

2011/2/11 updated. Feel free to link to this site.