
(Fig.1) No solution → just "choose" trial functions ! = useless

Schrodinger equation of two-electron helium contains interelectronic Coulomb energy. So it has No solution of helium.
They just choose artifical trial function as "imaginary" solution.
"Choosing" convenient hypothetical solution out of infinite choices means Schrödinger equation has no ability to predict multi-electron atoms.
And it's impossible to try infinite kinds of trial wavefunctions and find the one giving the lowest energy in them.
(Fig.2) Insert hydrogen solution e-r/a into Schrödinger equation ↓
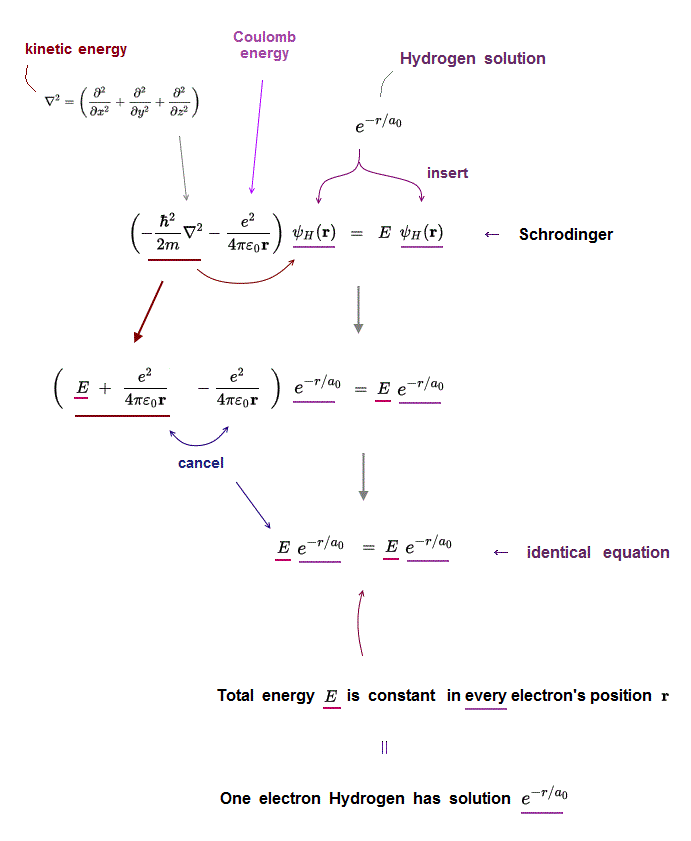
Only one-electron Hydrogen atom has its solution in Schrödinger equation.
Kinetic energy term just cancels out Coulomb energy term to satisfy Schrödinger equation in all electron's position r.
Inserting one of hydrogen solutions (ex. e-r/a ) into Schrödinger equation, you find its identical equation holds true in all position r.
(Fig.3) its kinetic energy terms must cancel all Coulomb terms.
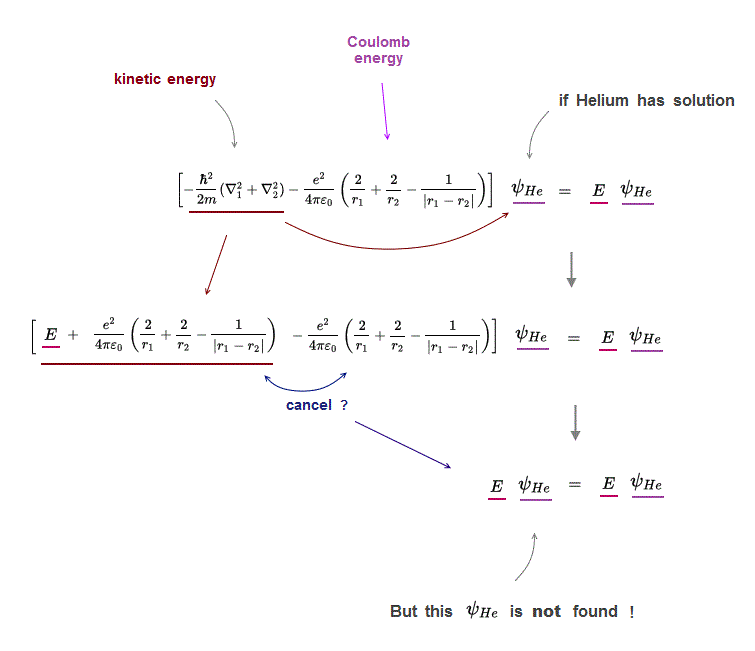
Why multi-electron atoms such as Helium don't have any exact solutions in their Schrödinger equations ?
If Helium has a solution (= ψHe ), when you insert it into Schrödinger equations, its kinetic energy terms need to cancel all Couloumb energy terms to get constant total energy E.
But there is a serious problem in Schrödinger wavefunction.
Schrödinger wavefunction always spreads all space. Its helium approximately consists of two hydrogen wavefunctions, so each electron of helium can move independently everywhere over spreading wavefunction !
It means these three different Coulomb terms must be independently canceled by its corresponding kinetic energy term → three "fake" hydrogens !?
(Fig.4) ↓ Helium atom can be divided into three unreal atoms ?
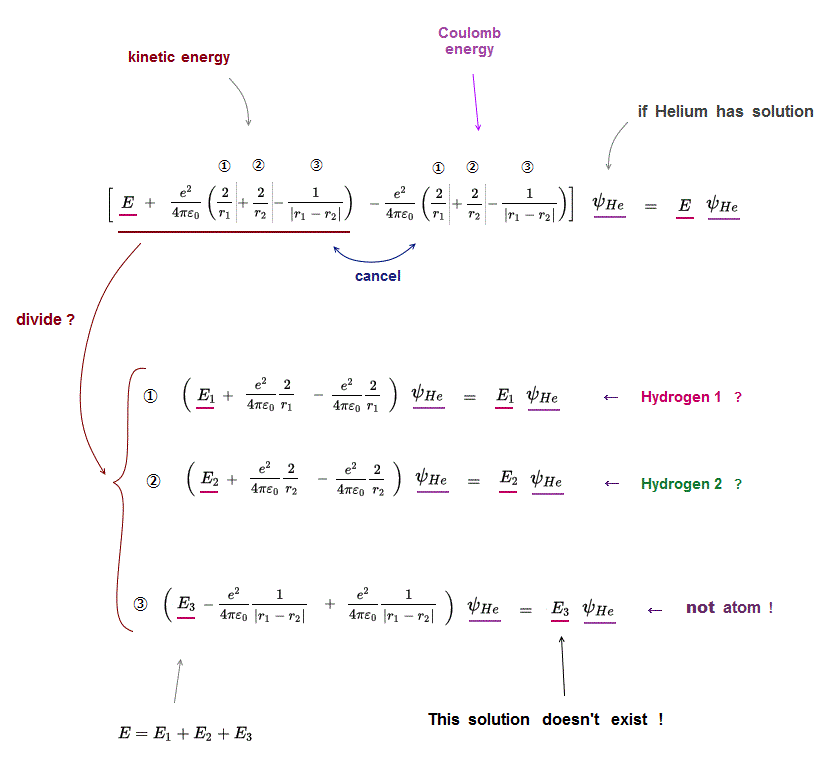
If Helium atom has its solution, it means Schrödinger equation holds true in all its electrons' positions (= r1, r2 ).
In Schrödinger equation helium, three Coulomb energy terms can be changed independently.
So each Coulomb energy term must be cancelled out independently by its corresponding kinetic energy term.
Coulomb term ① must be canceled by its kinetic term ① (← hydrogen ? )
Coulomb term ② must be canceled by its kinetic term ② (← hydrogen ? )
Coulomb term ③ must be canceled by its kinetic term ③ (← unreal atom ! )
This means Helium atom can be divided into three independent atoms which have NO relation to each other, if helium has solution !
Divided (= independent ) energy term cannot express the property specific to the whole atom or molecule.
(Fig.5) ①,② = hydrogen-like ? ③ = unreal electron-electron atom !

If Helium has its solution in Schrödinger equation, three different Coulomb terms have to be cancelled out independently by their kinetic energy terms.
It means, if a helium has solution, a helium atom can be divided into three independent atoms.
①,② are hydrogen-like atoms. ③ is a electron-electron atom which doesn't exist.
Furthermore, each of these three strange independent atoms doen't contain other atoms' information, which cannot describe the whole atom or molecule containing all informations !
For example, average electron-electron energies are different in different atoms or molecules due to their different nuclei.
But the above independent unreal atom (= ③ contains only electron-electron information ) cannot express it !
(Fig.6) ↓ Helium approximate quantum method is just fake !
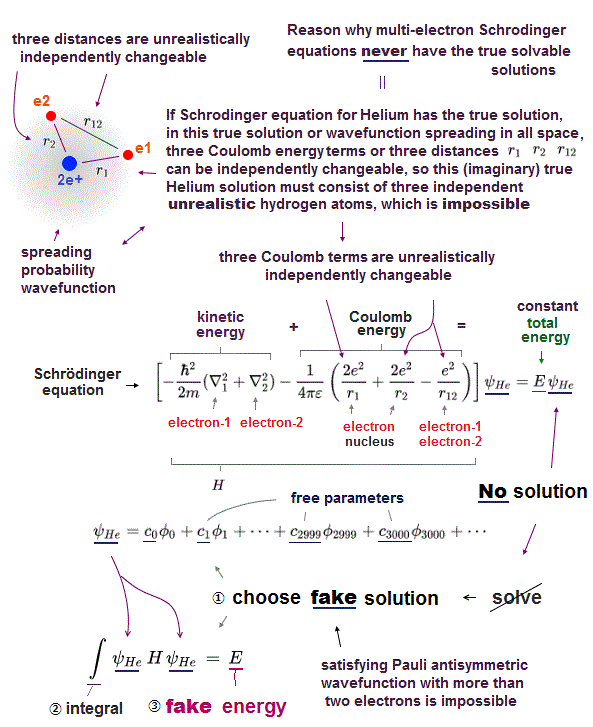
In Helium atom, the first thing you do is choose trial function as "fake" Helium solution, and insert it into Schrödinger equation.
After putting Schrödinger equation between two tial function (= ψHe ), you integrate it instead of solving it, because you cannot solve it.
The total energy E by this method is not true Helium energy.
You just repeat this ( choose different trial functions → insert → integral ) until you can get convenient fake energy.
You have to try infinite different trial functions as Helium fake solution and compare them to find the solution which gives the lowest ground state energy E.
But of course, it's impossible to try infinite kinds of trial function to find the lowest Helium energy E. So Schrödinger equation is useless in Helium.

2017/6/2 updated. Feel free to link to this site.