そのため、彼は 黒体の平均のエネルギー値を次のように定義した。
(Eq.1)
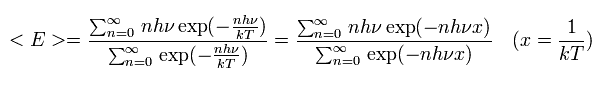
ここでは、分母は、
(Eq.2)
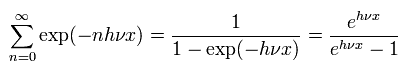
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは幻想である。
ド・ブロイ波による量子ホール効果。
プランク定数 (h) は 1899 年に マックス・プランクによって発見された非常に重要な概念である。
プランクは 黒体放射に関して調べていた。
もし 熱を持つ物体が黒いと それにぶつかる光をすべて吸収する。 そして平衡状態では熱による放射をしている。
ステファン・ボルツマンの法則によれば、温度 T のとき エネルギー E の状態である確率は exp (-E/kT) に比例する。
プランクは 振動数 が ν である電磁波が量子化されていると仮定した。( E = nhν ).
そのため、彼は 黒体の平均のエネルギー値を次のように定義した。
(Eq.1)
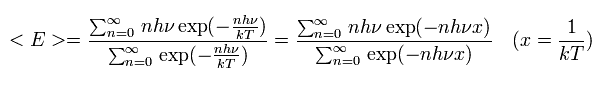
ここでは、分母は、
(Eq.2)
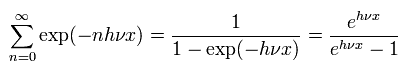
また、Eq.1 の分子は、
(Eq.3)
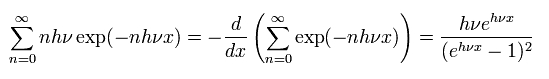
Eq.2 と Eq.3 を Eq.1 に代入すると、E の平均は、
(Eq.4)
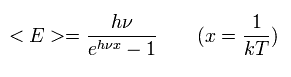
Eq.4 の計算結果から、プランクは 6.55 × 10-34 Js の プランク定数を得た。これは次の現在の最新値とほぼ等しい。
(Eq.5)
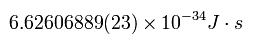
Eq.4 の関係式は Rayleigh Jeans と Wien の式を含んでいる。
Eq.5 の プランク定数は 後で説明する ワット・バランス (Watt balance ) によって得られたものである。
(Steiner R et al, J. Res. Natl. Inst. Stand. Technol. 2005, 110, 1-26)
1905 年、アインシュタインは 光電効果を提案し、1916 年、ロバート・ミリカンが 光電効果を使って実験によって プランク定数を求めた。
彼のプランク定数は 6.57 × 10-34 Js で、プランクの仮説とほぼ同じであった。
重要な点は プランクやミリカンのプランク定数は 電磁波のド・ブロイの関係式をベースにしていることである。
また ワット・バランス法や ジョセフソン効果によるものは 電子の ド・ブロイの関係式をベースにしたものである。
つまり、このことは 黒体放射の量子化されたエネルギーは 電子の量子化された ド・ブロイ波 に基づいていることを示唆している。
後に、中性子の ド・ブロイの関係式が ブラッグ反射によって 精密に測定され、これは 微細構造定数 の計算にも利用されている。この プランク定数は Eq.5 の値とほぼ変わらない。
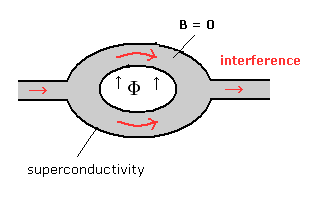
超電導体リングを通過するとき、磁束 (Φ) は 量子化されることが知られている。
弱い磁束が 超電導リングに入ると、リングの磁束に接する境界付近に 磁束をキャンセルする電流が流れる。
結果として、超電導物質本体 (superconductivity) の 磁束密度は ゼロ ( B = 0 ) になる。
これを "マイスナー効果" と言う。
(磁束近くの部分のみ、磁束密度 B はゼロにならず、電流が存在する。)
(Fig.1)
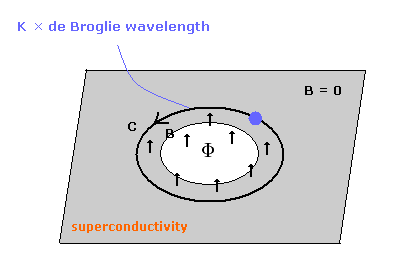
磁束量子 (Φ0) は 超電導体を通過する 量子化された磁束である。
磁束の量子化は アハラノフ・ボーム効果 と深い関係があるが、もとは 1948 年に Fritz London によって提唱された。
(Eq.6) 超電導では磁束は量子化される。
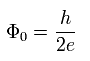
Eq.6 を使って 正確なプランク定数 (h) を得ることができる。
最初に シュレディンガー方程式を使って Eq.6 を求めることにする。
シュレディンガー方程式で Eq.6 を得るには、2つの電子からなる "クーパー対(ペア)" を想定しなければならない。
( クーパー対が "人為的な"概念だという可能性はないだろうか? )
超低温の超電導体では Eq.7 に示すように すべての電子の 位相がそろう傾向にある。
ところで、この電子の位相とはいったい何なのだろうか ??
(Eq.7) 超電導体における波動関数。
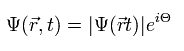
ここでは 位相 (Θ) は 次のように 運動量 (p) と エネルギー (E) から成る。
(Eq.8)
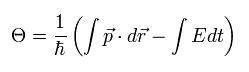
もし 2つの電子間の 反発力を忘れて ”クーパー対 ( -2e )” を仮定すれば、運動量 (p) と エネルギー (E) は次のようになる。
(Eq.9)
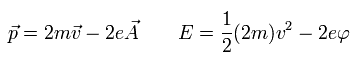
ここでは ローレンツ力 を使っている。 このページも参照のこと。
空間部分のみに注目すると、Eq.8 は、
(Eq.10)
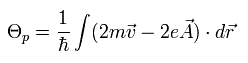
Fig.1 の穴の周囲を一周して、波動関数の位相が元に戻ることを考慮すると、
(Eq.11)
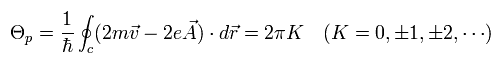
ここで K は 整数である。
マイスナー効果によれば、超電導体における 磁場や電流は無視できる。
そのため、Eq.11 の 電子の速度 (= v ) をゼロにすることができる。
(Eq.12)

ここで、 Φ は 磁束を意味しており、マクスウェルの法則によれば ベクトルポテンシャル (= A ) に囲まれたものである。
アハラノフ・ボーム効果 によれば、ベクトルポテンシャル (= A ) は 磁束密度 (= B ) がゼロのところでも存在する。
Eq.12 から、穴の部分の磁束密度 (Φ) は 次のように 量子化される。
(Eq.13)

ここでは
(Eq.14)
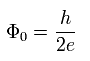
Eq.14 は "磁束量子 (Wb)" と呼ばれるもので、 正確なプランク定数を得るのに使われる。
Eq.14 の逆数を "ジョセフソン定数" と呼ぶ。
ところで、我々は この 位相なるものが何なのか ぜひとも知りたいものである。
ここで 電子が 磁場をキャンセルするために Fig.1 の穴の周囲近くを周回しているとする。
遠心力が ローレンツ力に等しいとき、
(Eq.15)
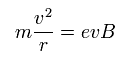
軌道1周 が ド・ブロイ波長の整数倍 に等しいとすると、
(Eq.16)
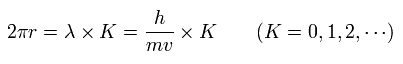
Eq.15 と Eq.16 から、 次を得る。
(Eq.17)
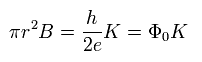
Eq.17 は 次のように Fig.1 の穴の部分を通過する 磁束 (Φ) を意味している。
(Eq.18)
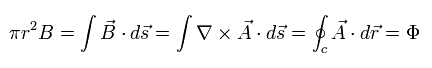
よって、我々は ド・ブロイ波と 古典力学の概念を用いることによって、Eq.13 と Eq.14 の 量子化された磁束を得ることができた。
これはつまり "ミステリアスな" 位相なるものは 穴近くを周回する電子の ド・ブロイ波 であることを意味している。
また、驚くことに、Eq.15 と Eq.16 においては、"奇妙な" クーパー対なるものを使用する必要がないのである。
もともと ”クーパー対”なるものは スピン効果を打ち消すために "意図的に" 導入されたものだと個人的には思う。
( もし 電子スピンなるものが実在すればの話である。 )
あなた達は、どう思われるだろうか?
ジョセフソン効果とは 薄い絶縁体によって隔たれた 超電導体の間を 電流が流れる現象である。
この 2つの超電導体が 非伝導体バリアによって結合しているものを "ジョセフソン結合" と呼ぶ。
1962 年に、ジョセフソンが この効果を予想し、それは SQUIDs などの 量子力学的な circuit で重要な意味を持つ。
ジョセフソン結合のバリアはとても薄いため、弱い刺激を与えれば 電流が流れることができる。
しかし 超電導体などの 無磁場 の状態でさえも このバリアに電流が流れる。(量子トンネル効果。)
もし ド・ブロイ波 によって この量子トンネル効果を説明できれば、このことは ボーア模型によって ジョセフソン効果と量子トンネル効果を説明できる ことを意味する。
(Fig.2) ジョセフソン結合。
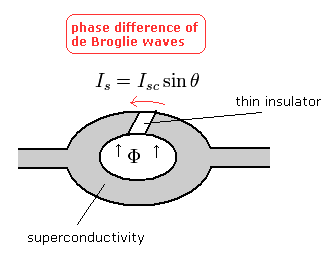
直流ジョセフソン効果とは トンネル効果によって 電磁場が存在しない状態でも 絶縁体間を直流電流が流れる現象である。
(もちろん、超電導の磁場をゼロにするのは 穴付近の電流は Φ をキャンセルするために存在する必要がある。)
この 直流ジョセフソン電流は 次のように 絶縁体を挟んだ位相差の sine に比例する。
(Eq.19)
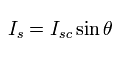
ここでは 位相差 θ は次のように表せる。
(Eq.20)
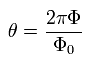
Eq.19 と Eq.20 は 穴の部分の磁束 (Φ) が 磁束量子の整数倍のとき、位相差がゼロになり ジョセフソン電流が生じない。
つまり、我々は ジョセフソン結合は 穴付近の電子のド・ブロイ波の影響を受ける と主張することができる。
よって、量子トンネル効果とは 電子の ド・ブロイ波によって生じるものなのである。
接合間の電位 V を固定すると、位相は 時間とともに 直線状に変化し、電流は交流になる。
(交流ジョセフソン効果.)
マクスウェル方程式によれば、 Fig.2 のリングの電位は次のように表せる。
(Eq.21)
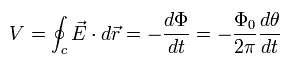
ここでは Eq.20 を使っている。
Eq.21 を 時間 t で積分すると 次を得る。
(Eq.22)
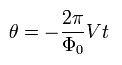
Eq.22 を Eq.19 に代入すると、 次の 交流ジョセフソン電流を得ることができる。
(Eq.23)
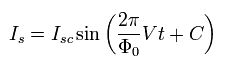
Eq.23 の振動数 は
(Eq.24)
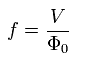
Eq.24 の 振動数は これと同調する マイクロ波で確認することができる。(シャピロステップ。)
そして、この測定された 電圧 (V) は 電圧標準の定義として使用される。
また ジョセフソン効果は Φ0 に プランク定数 (h) が含まれているため、その定義にも使われる。
(もちろん、このプランク定数は Eq.16 の 電子の ド・ブロイの関係式に由来している。)
アハラノフ・ボーム (AB) 効果とは、荷電粒子が 磁場 B や 電場 E が存在しないところでも、間接的に 電磁場の影響を受ける現象である。
そのメカニズムは 電磁ポテンシャルと 荷電粒子の波動関数の相互作用によるとされている。
最もよく登場するケースは、とても長いソレノイドの周囲で 磁場はゼロだが、ベクトルポテンシャルは存在する領域を 荷電粒子が通過するときに その波動関数が 位相変化を受けるという場合である。
この位相変化は 実験で観察されている。
最初に、量子力学的な方法で AB 効果を説明することにする。
(もちろん、ここでも 古典的な ローレンツ力を使用している。)
ベクトルポテンシャル (A) と スカラーポテンシャル (φ) を使って、電磁場のもとでの 電子のハミルトニアンは、
(Eq.25)
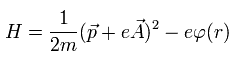
これはローレンツ力を意味している。このページも参照のこと。
マクスウェル方程式によれば、電場 (E) と 磁場 (B) は 次のように表せる。
(Eq.26)
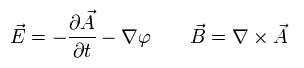
もし これらを次のように変化させると、E と B は Eq.26 と同じ関係式を用いて 新しい ベクトル、スカラーポテンシャルで表すことが可能である。
(Eq.27)
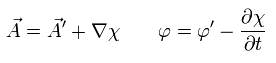
ここで χ は 任意の 値である。
( Eq.27 を Eq.26 に代入してみるといい。 )
これを "ゲージ変換" という。
次に Eq.25 をシュレディンガー方程式で表す。
(Eq.28)
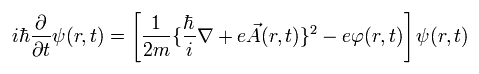
ゲージ変換後も Eq.28 と同じシュレディンガー方程式を満たす必要がある。
(Eq.29)
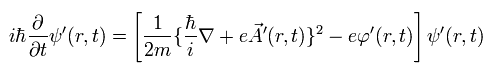
ここで、ゲージ変換後の波動関数を次のように仮定する。
(Eq.30)
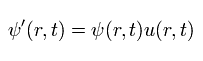
Eq.30 と Eq.27 を使って、Eq.29 の エネルギーとスカラーポテンシャルの項は次のようになる。
(Eq.31)
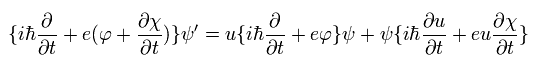
また、Eq.29 の運動量とベクトルポテンシャルの項は次のようになる。
(Eq.32)
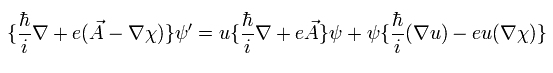
Eq.32 には もう一回 次のように 演算子をかける必要がある。
(Eq.33)
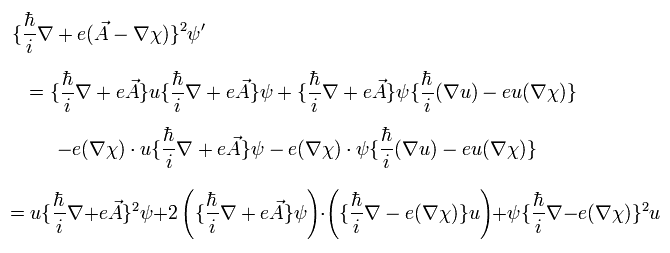
ここで ( ... ) の中の ∇ は 外の関数に作用しない。
Eq.31 と Eq.33 を Eq.29 に代入すると、次の関係式を満たすとき、それは Eq.28 と一致する。
(Eq.34)
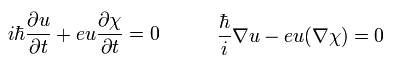
Eq.34 の解は、
(Eq.35)
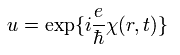
つまり Eq.30 は、
(Eq.36)
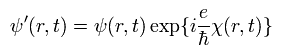
ここで 磁場は 半径 r0 の ソレノイドの中に限定されると仮定する。
(ソレノイドの外側の磁場はゼロとする。)
そのため、ベクトルポテンシャル (A) は次のように表せる。
(Eq.37)
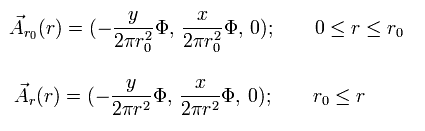
Eq.26 と Eq.37 から、 磁束密度 (B) は、
(Eq.38)
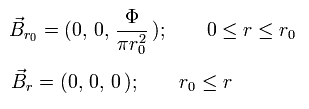
ここで、
(Eq.39)
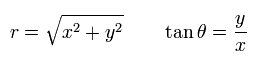
Eq.37 より、ソレノイドの外側のベクトルポテンシャルは 次のように "接線方向" のみ存在する。
(Eq.40)
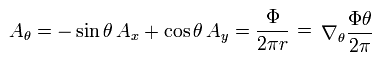
ここで、
(Eq.41)
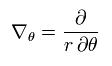
Eq.40 より、Eq.27 の ゲージ χ を 次のように仮定すると、A' はゼロになる。
(Eq.42)
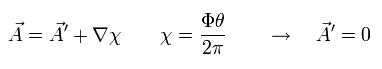
この状態のとき、元の波動関数は 次のようになる。
(Eq.43)
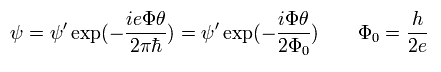
Eq.43 によれば、波動関数の位相は 2 × Φ0 単位で変化する。
(この結果は 上の磁束量子の結果と異なるように見える。)
(Fig.3)
長いソレノイドの代わりに、超電導体を使う。すると、Fig.3 に示すように 磁束は 穴と その付近のみに限定される。
ここで電流を流して 穴の 磁束 (Φ) を変化させ 電気抵抗を測定する。
2つの通路からの 電流は互いに干渉して その干渉パターンによって 抵抗が変化する。
実験結果は 電気抵抗が 2 × Φ0 の周期で変化した。
これは Eq.43 のシュレディンガーの波動関数が 正しいという意味なのであろうか?
(Fig.4)
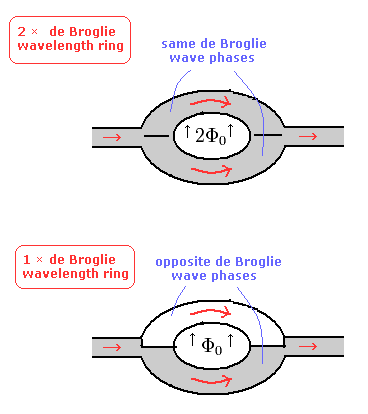
ボーアモデルの ド・ブロイ波によれば、磁束量子 が 2 × Φ0 のとき、2 × ド・ブロイ波 が 軌道1周に含まれる。(Fig.4 の上の図。)
この場合は、2つの電流は 同じ位相のド・ブロイ波の影響を受ける。
しかし 磁束密度が 1 × Φ0 (Fig.4 の下図) のとき、2つの電流は 異なった位相の ド・ブロイ波の影響を受ける。
結果として、干渉パターンは 2 × Φ0 周期で変化する。
ジョセフソン効果などの章で クーパー対 (= -2e ) を使っていたにも関わらず、 上のシュレデインガー方程式が クーパー対を使用しないことは 不自然である。
一方で、ボーアモデルによる ド・ブロイ波は "自然に" アハラノフ・ボーム効果を説明することが可能である。
プランク定数測定の最も精密な方法は、”ワットバランス”法 である。
ここでは ワットバランス法について説明し、水素原子のエネルギー準位が そのプランク定数で正確に表せるか調べることにする。
(Fig.5)
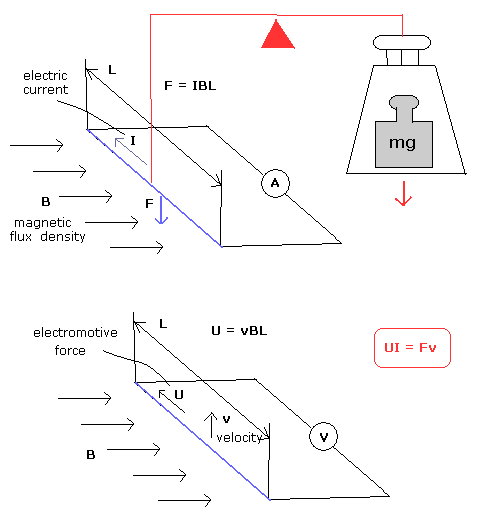
長さ L の 導体のワイアに 磁場 B に垂直な方向に電流が流れており、IBL の力を受ける。(Fig.5 の上図。)
ある質量に重力定数gをかけた mg の力に釣り合うように その電流を変化させる。
電流を正確に測定するためには、量子ホール効果によって定義された "標準の電気抵抗" を使用する必要がある。
強磁場と超低温の 2次元電子系において、ホール伝導度が量子化 ( e2/h ) されることが知られている。
このホール効果の プランク定数も 電子のド・ブロイ波に由来する。
(ド・ブロイ波による量子ホール効果。も参照のこと。)
この量子化された値は 電気抵抗標準の定義に使用される。
同じ ワイアを同じ磁場 (B) の中を 速度 v で運動させる。(Fig.5 の下図。)
ファラデーの誘導法則によれば、電位差 U が ワイアに生じて その大きさは vBL に等しい。
そのため、未知の量である B と L が次の関係式から除去される。
UI = Fv
上の電位差 U は Eq.24 の ジョセフソンの方法によって精密に測定できる。
結果として、ジョセフソン効果と ホール効果に基ずく プランク定数の正確な値を得ることができる。
(よって、ワットバランス法は 電子の ド・ブロイの関係式のプランク定数を表していると言える。)
上のワットバランス法は 水素原子スペクトラムから得られる リュードベリ定数を使用していない。
そのため Eq.5 のプランク定数を用いて 水素原子の実験値を正確に計算することができれば、ワットバランス法によるプランク定数は 正しいことが証明される。
ボーア模型の水素では、遠心力がクーロン力に等しい。
また、軌道長は 次のように ド・ブロイ波長の 整数倍である。
(Eq.44)
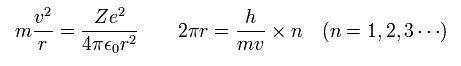
Eq.44 から、次の 半径 (r), 速度 (v), エネルギー (E) を得ることができる。
(Eq.45)
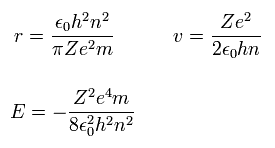
トップページに示すように、我々は 実験値に等しい 精密な新しいボーアのヘリウムをあらわすことに成功した。
この新しい方法では、微小時間ごとに 微小移動区間に含まれる クーロン力と ド・ブロイ波の数を計算した。
コントロールとして、我々は この新しいボーアのヘリウム法を用いて ボーア模型の水素原子の基底状態のエネルギーを計算してみることにする。
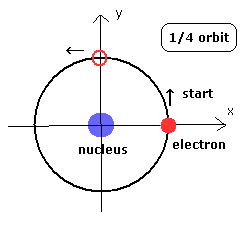
(Fig.6) ボーアの水素原子の 1S 軌道。
ボーアの 1S 水素原子軌道計算の サンプル JAVA プログラム。
中のソースプログラムをそのままテキストエディタ(メモ帳など)にコピー and ペースト すれば、簡単にコンパイルと実行できる。
(この class file name は Hyatom なので、このテキストエディタを "Hyatom.java" とセーブしてコンパイルしてほしい。)
上のプログラムでは、次の新しい単位を使用する。
(Eq.46)
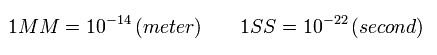
Eq.46 から、 速度と加速度は、
(Eq.47)
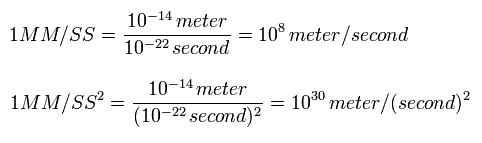
1 SS (= 10-22 sec ) ごとに、クーロン力から 加速度の x と y 成分を 次のように計算する。
( 軌道は x-y 平面にあると仮定する。)
(Eq.48)
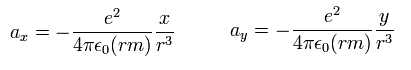
ここでは (rm) は 水素原子の換算質量を意味する。
また、1 SS ごとに、微小移動区間に含まれる ド・ブロイ波の数を計算して それを次のように足し合わせていく。
(Eq.49)
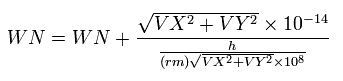
ここでは 分子は 1 SS ごとの 移動距離 (meter) を意味し、分母は ド・ブロイ波長 (meter) を意味している。
VX と VY は 速度の成分 (MM/SS) を意味している。
また、上のプログラムは Eq.45 を使って、全エネルギー |E| と 半径 (MM) の理論値も計算している。
その結果を Table 1 に示す。
last VY ( 1/4 周後の 電子速度の y 成分 ) がゼロのとき、電子軌道は 安定になる。(Fig.6 参照。)
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -13.580 | 5301.0 | 0.25017 | 1.00068 |
| -13.590 | 5297.0 | 0.25008 | 1.00032 |
| -13.5983 | 5294.5 | 0.25000 | 1.00000 |
| -13.600 | 5294.0 | 0.24999 | 0.99996 |
| -13.610 | 5290.0 | 0.24989 | 0.99956 |
全エネルギーの 実験値は、-13.59844 eV である。
エネルギーの相対論的な補正値 は -0.00014 eV で、この値は適切である。
Eq.45 からの エネルギーの理論値は -13.5983 eV である。
また、Eq.45 からの半径の理論値は 5294.65 (MM) である。
これらの理論値は 上の Table 1 の計算値に 一致する。
このことは、ボーアのヘリウムで使用したコンピューター計算法も正しかったことを意味している。
もし 換算質量を用いなかったら、結果は -13.606 eV になり、これは 実験値と異なる。
この事実は 電子と原子核が 重心の周りを 実際に回っていることを示している。
光子のプランク定数 h は 電子(もしくは中性子)の ド・ブロイ波と同じ値である。
ということは、ボーアモデルの水素原子から 光子(電磁波)の 量子化された 振動数を得ることはできるのだろうか?
ボーアの 1S 軌道では、軌道の長さは 次のように ド・ブロイ波長に等しい。
(Eq.50)
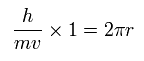
そのため、電子の振動数 (= f ) は 次のように表せる。
(Eq.51)
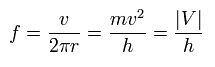
ここでは 次の関係式を使う。
(Eq.52)
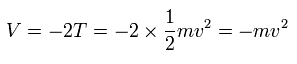
Eq.51 は Eq.51 の振動数 (f) の電磁波をあてると、それは ボーアの 1S 電子の運動に 同調することを意味する。
結果として、1S 電子は "元の" 速度 (v) を保ったまま 放出される。
つまり、照射される電磁波の振動数は 電子を束縛する クーロンエネルギーをキャンセルする量に一致する。
2S の ボーアの電子の場合は どうであろうか?
2S では、軌道長は 次のように ド・ブロイ波長の2倍になる。
(Eq.53)
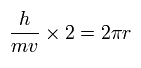
そのため 電子の振動数は、
(Eq.54)
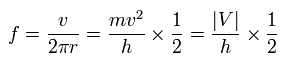
この結果は Eq.51 のと違うように見える。
しかし、2S 軌道は 2つの ド・ブロイ波の位相を含んでいるため、1/2 回転で 波の位相が戻ることになる。
よって、Eq.54 では、2π r のかわりに π r を使うと、次を得る。
(Eq.55)
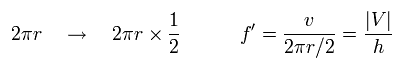
Eq.55 の結果は ボーアの 1S 軌道の Eq.51 にちょうど等しい。
このことは、照射した電磁波の振動数は クーロンエネルギーをキャンセルする 電子の振動数と一致することを意味する。
電子軌道の各地点における ド・ブロイ波は振動している。
Eq.55 の場合は、電子が その軌道を半周する間に 軌道の各地点は 1回 振動する。
つまり、電磁波は 軌道の各地点のド・ブロイ波に作用すると考えられる。
(Fig.7) 放射された電磁波の振動数。
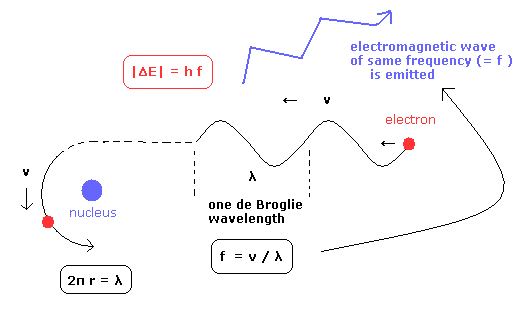
次に 放射される電磁波の場合である。ボーアの 1S 電子と等しい速度 v の自由電子が 1S 軌道に落ちていく過程を考える。
(結果として、速度 v は 変化しない。)
もし、自由電子のド・ブロイ波の振動数が 放射される電磁波に等しいをすると、それは E = hf の関係式を正確に説明できる。
これらの結果は 電磁波の量子化された振動数は ボーアの電子の ド・ブロイ波の振動数に関係していることを示唆している。
さらに 運動エネルギーの変化を考慮すると、光電効果は ボーア模型と "古典的な"電磁波によって説明可能である。
運動エネルギーの場合は 最初から ド・ブロイ波 として 表されているため、それは コンプトン効果に示されるように 簡単に電磁波と相互作用できる。

2011/6/22 updated This site is link free.