トップページ (2電子原子も含む正確な新ボーア模型)
シュレデインガー方程式はボーアゾンマーフェルト模型の間違いバージョンである。
リーマン,リッチ,アインシュタインテンソルの導出
シュヴァルツシルト解の導出と GPS 時間補正。
相対論は電磁気学において破綻している。
最初に 特殊相対性理論と量子力学の緊密な関係について簡単に振り返ってみる。
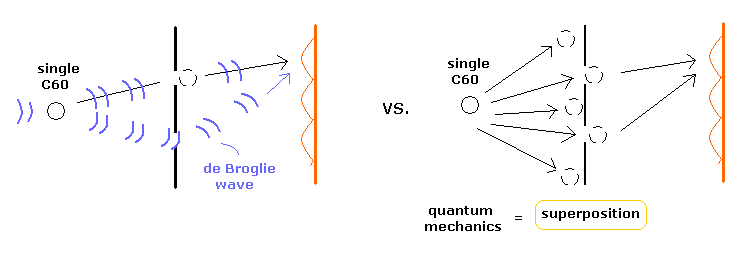
(Fig.1) 単一の C60 のフラーレンが自分自身と干渉する。

相対性理論は いわゆる "エーテル" を否定し、最高スピードである光速を順守するために 時間と空間が伸び縮みして調節するという奇妙な概念を導入した。
つまり 電子などの波動関数に "実在の"ドブロイ波を使用できないことになる。なぜなら Fig.1 左に示すように "実在"のドブロイ波は "エーテル"に他ならないからだ。 ( このページも参照のこと。 )
量子力学における 超光速の ( もしくは 多世界様の ) 波動関数の収縮は 現実性がないに等しい。
Fig.1 の右の量子力学によれば 2重スリットにおいて 単一の C60 分子が 多世界様の重ね合わせの原理で 何と 同一時間にあわゆる場所に存在できることになる。
これはつまり 非現実性の量子力学と エーテルの実在性を否定した相対論は 手を結びあっているということになる。
(Fig.2) 相対論によれば 空間は 非常に多くの種類の粒子であふれかえっている。
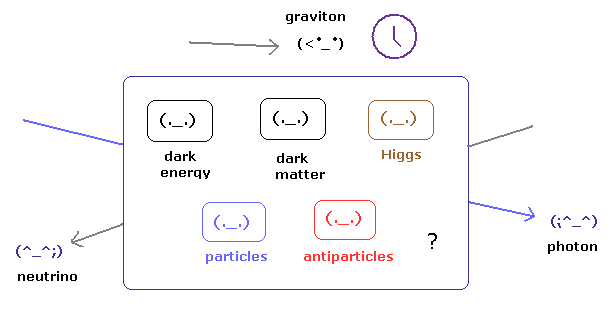
基本的に ファンタジーの世界は別として この世界には 空間は1つしかない。
ご存じのとおり、特殊相対論は 真空中の "エーテル" を否定したので 真空の空間には 何も含んではいけないことになる。
しかし 現在の相対論的な場の量子論によれば、真空中には ダークエネルギー、ダークマター、ヒッグス粒子、粒子と反粒子の無限のペアなどの非常に多種類の粒子や物質であふれかえっているのである。
さらに 光子やニュートリノなどは これらの非常に混みあった空間内を まったく"無傷"な状態で 通り抜ける特殊能力があることになる。
そして 重力子は 力としてだけでなく 奇妙な時間の遅れを引き起こす能力があることになる。
しかし こんなにいろんな物質であふれかえった空間上を うまい具合に 光子やニュートリノが素通りできる モデルは はっきり言って無理がありすぎると思われる。
(Fig.E-1) 1つの電線が 2つに分離??
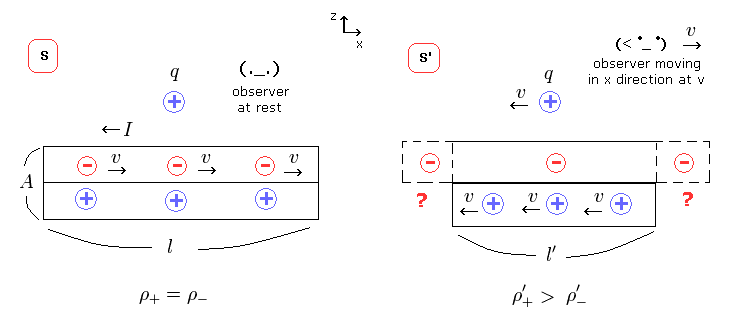
このページに示したように、相対論による電荷と電流密度の関係式によれば、何と 観測者の単純移動だけで 中性の電流 (= プラスとマイナスの電荷数が同じ ) から 奇妙な電荷を発生させてしまう。
例えば Fig.E-1 の s 慣性系の視点からは 誰か電線に対して静止している人がある決まった電線の両端を切断したとしよう。
その中性の電線の内部には 同数のマイナスとプラスの電荷が入っているだろう。
しかし s' の視点 (= Fig.E-1 の右 ) から 同じ人が決まった電線の両端を切断すると 何とそこには プラスの電荷のほうが多く含まれていることになる。
これはつまり 明確にローレンツ変換自体が間違いということになる。
(Fig.E-2) 2つの同一の人工衛星における 双子のパラドックス
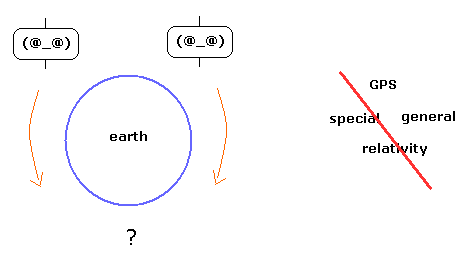
特殊相対論によれば、ローレンツ変換不変な固有時間は 動く物体に伴った時計の時間を示している。
ある観測者 (= A ) の視点からは 別の観測者 (=B ) の固有時は必ず遅れることになる。
しかし 観測者 B の視点からは A の固有時が必ず遅れることになる。
これが有名な "双子のパラドックス" である。
このページに示したように、2つの同一の人工衛星が 地球周囲の同一の軌道上を正反対の方向に進んでいるとすると、それらの固有時はパラドックスを示すことになる。
( 一般相対論と遠心力ポテンシャルを考慮すれば これが立派にパラドックスであることを示すことができる。)
つまり 有名な GPS における相対論の補正は 特殊相対論による補正も行っているため 双子のパラドックスを含んでいることになる。
[ 偉人達の量子論に対する格言 (英文) ]

最も重要なことは 量子力学上最も重要な貢献をした シュレディンガー自身が 現在の波動関数の確率解釈に同意していないことである。
彼は かの有名な シュレディンガーの猫を用いて 量子力学を批判した。
シュレディンガー、アインシュタイン、ド・ブロイは 実在主義者だった。
アインシュタインは 生涯 量子力学を認めなかった。
( 「迷走する物理学」 リー・スモーリン著 参照のこと。 )
また 量子力学の偉人の1人である ディラックは 量子電磁力学の 発散繰り込み手法に批判的だった。
驚くべきことに、後に 彼は "エーテル"を復活させようとしていたらしい。( 「量子の海、ディラックの深淵」グレアム・ファーメロ著 参照のこと。)
ファインマンは 10次元の超ひも理論に批判的だった。
つまり 現在の量子論は 物理界の偉人達の承認を得ていないのである。
これはとても重要なことである。
良く知られているように、クーロン力とローレンツ力などの 電磁気力は 我々の世界で重要な役割を果たしている。
一般相対論は 重力を説明するために導入された。
では 重力と電磁気力の違いは何なのだろうか??
(Fig.3) 重力版 電磁気力は存在しない。
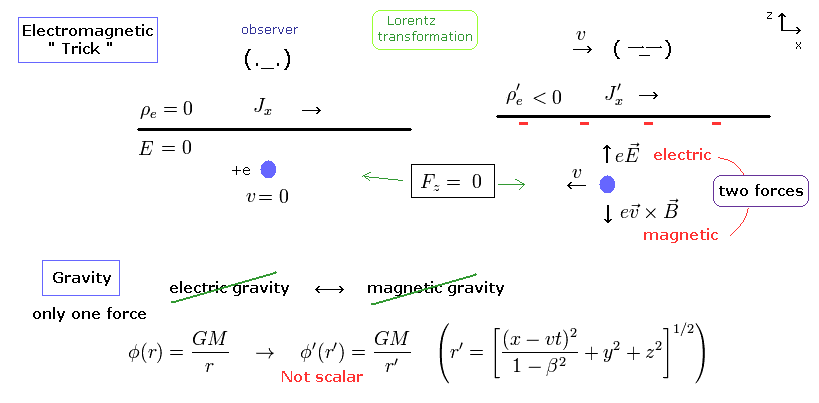
特殊相対論によれば、世界中のすべての物理現象は いかなる慣性系でも同じように見えなければならない。
これは 観測者が 異なった速度で運動しているときでさえ、対象物の反応は同じに見えることを意味している。
電磁気力には クーロン力 (= 電場の力 ) と ローレンツ力 (= 磁場の力 ) の2種類の力が存在する。
これらの2つの異なった力を うまく組み合わせることによって、電磁気学は 特殊相対論に組み入れられた。
( しかし このことによって 非常に奇妙な観測者の超能力を生じることになってしまった。このことは後で説明するが・・)
相対論は電磁気学で破綻している。も参照のこと。
もちろん 地球とともに動くエーテルを認めれば これら奇妙なローレンツ変換や 相対論の非常に厳しい制限を使用する必要がなくなるので この電荷と電流のパラドックスも消失する。
しかし 重力には たった1種類の力しか存在しない。
つまり 重力は このトリックが使用できない。
また ローレンツ変換による 異なった慣性系において 重力の関係式 ( GM/r ) が Fig.3 に示すように変わってしまう。(= つまりスカラーではない。)
すなわち 重力の関係式は 動く観測者には 異なって見えることになる。
この深刻な状態 (= "数学的な"理由によるが ) を回避するために、重力を キャンセルさせて 特殊相対論にマッチさせる必要がでてきた。
これが ( 重力を消去した )局所慣性系と呼ばれるものである。
(Fig.4) 観測者 (= observer ) は 対象物に触れることなく重力を消去できるのか ??
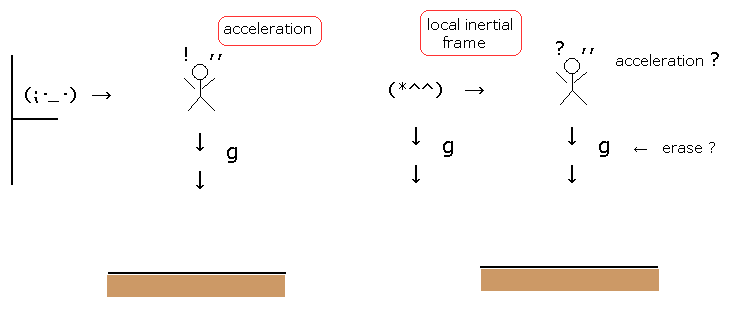
重力によって地面に向かって落下している人がいるとしよう。
もちろん、静止している観測者 (= Fig.4 の左 ) から見ると 対象の人は 重力の影響を受けているように見えることは間違いない。
しかし 一般相対性理論によれば 重力に従って落下している観測者からみたら 対象の人は重力の影響をまったく受けていないことになっている。( Fig.4 の右 )
そのため この状態では いわゆる ローレンツ共変な ミンコフスキー慣性系を使用できることになる。これを等価原理という。
しかし 本当にそうだろうか?
対象に何ら触れたりしない観測者がどういう行動をしようが、重力によって落ちている対象の人間は 重力を感じていることはあたりまえの話である。
光は質量ゼロのため 重力はゼロ ( m × g = 0 ) である。しかし Fig.10 のように 一般相対論はいつのまにか 上記の論理を光のものにすり替えてしまうのである。
つまり 一般相対論では 観測者は 対象の重力を消去させる力があることになっている。
もし 通常のミンコフスキー空間に移行して特殊相対論を使えないとしたら、一般相対論は無意味なものになってしまう。
一般相対論においても 特殊相対論は必要不可欠なものなのである。
よって特殊相対論が間違っていると 一般相対論も間違いということになる。
(もちろん 特殊相対論が 重力を説明できないので 一般相対論も相対性理論にとっては必要である。)
最初に ローレンツ変換の基本的なルールについて説明する。
もし このページをまだ読んでいなければ 先に読むように。
(Fig.5) 2つの慣性系 ( K と K').
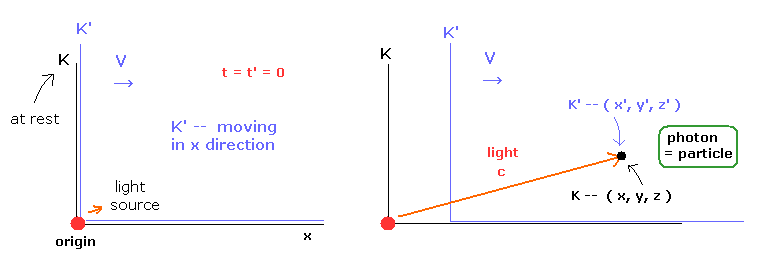
Fig.5 に示すような K と K' の2つの慣性系があるとする。
K' の慣性系は K に対して 速度 v で x 方向に動いている。
各時空から見た座標は K では ( t, x, y, z )、K' では ( t', x', y', z' ) である。
t = t' = 0 の時間のとき、これら2つの慣性座標系の原点は 空間上の同一地点にあるとする。
また t = t' = 0 のとき、原点の光源から光が放出されるとする。
もし 光の速度が いかなる慣性系においても c だとしたら 次の方程式を満足しなければならない。
(Eq.1)
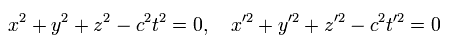
ここで t と t' は K と K' の慣性系からみた時間である。
K' の (x', y', z', t' ) が 次の関係式をみたしているとき、
(Eq.2)
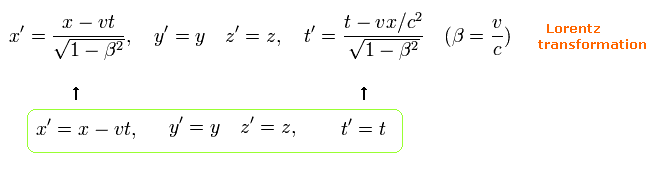
Eq.2 を Eq.1 に代入してみれば Eq.1 の関係が成り立っていることがわかる。
(Eq.2')
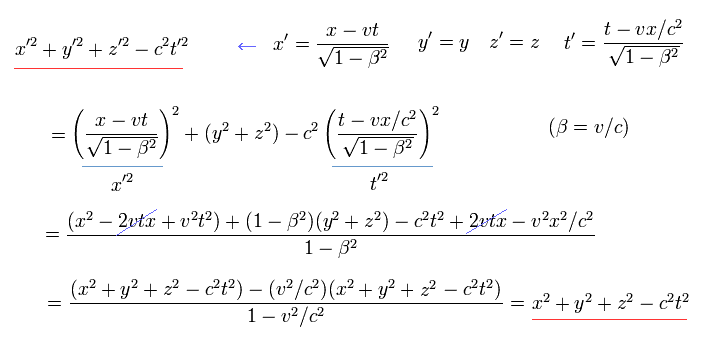
Eq.2 は x 方向への "ローレンツ変換" のブーストという。
一般的には スカラーの距離=世界長さ (= s2 or ds2 ) は 4元ベクトルの二乗で表される。
(Eq.3)
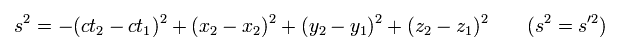
Eq.2 のローレンツ変換は 次のように行列で表すことができる。
(Eq.4)
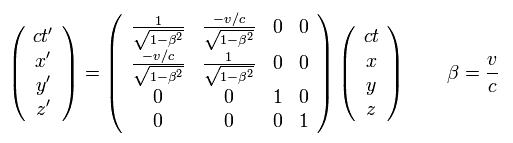
そのため 時間変数として t の代わりに x0 = ct を使うと便利である。.
(Eq.5)
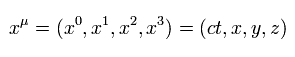
添え字 (= 0, 1, 2, 3 ) が Eq.5 のように上側にあるとき、これを 反変ベクトル (contravariant vector) と呼ぶ。
Eq.5 を使うと、 Eq.4 のローレンツ変換は次のように表せる。
(Eq.6)
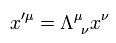
ここで ローレンツ変換の行列は、
(Eq.7)
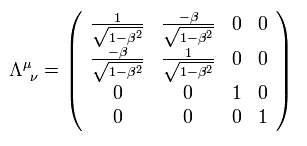
1つの項で 同じ文字を2回使用すると ( Eq.6 の ν のように ), これは その文字に対して ν = 0 + 1 + 2 + 3 と合計することを意味する。
例えば、Eq.7 を用いると ct' は、
(Eq.7')
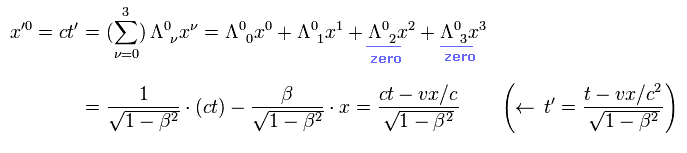
これは Eq.2 に等しい。
また ミンコフスキー空間の計量テンソルを次のように定義する。
(Eq.8)
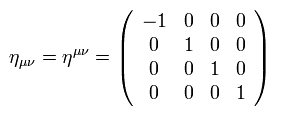
注意: このページでは η が ミンコフスキーの計量テンソルを表す。 "g" は 一般化した計量テンソルを表し、これは 4元ベクトル xμ の関数である。
このミンコフスキーの計量テンソルを用いると、 共変ベクトル (covariant vector) は、
(Eq.9)
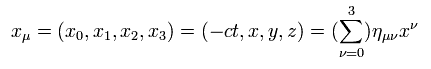
つまり 添え字が下にあるとき、 x0 = - ct のみマイナスとなる。
Eq.8 と Eq.9 の意味は、
(Eq.9')
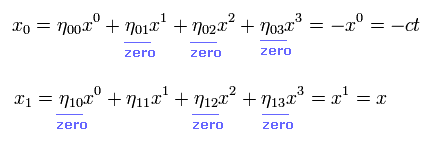
これらの反変 共変ベクトルを用いると、 Eq.3 のスカラー距離は、
(Eq.10)
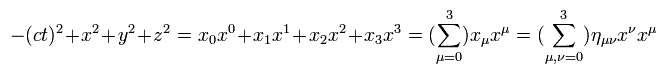
Eq.8 より
(Eq.11)
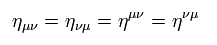
と
(Eq.12)
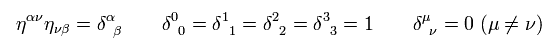
ここで δ は "クロネッカーのデルタ" である。
Eq.12 は ηη = 1 (単位行列) を意味している。
Eq.6 は 次のように表せる。
(Eq.13)
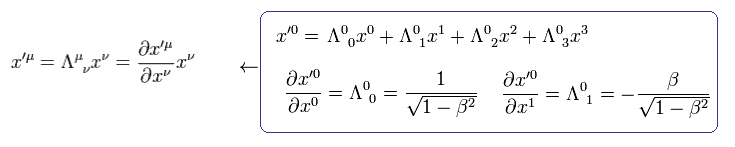
Eq.13 は 反変ベクトルの変換を表している。
Eq.10 と Eq.13、 スカラー距離はローレンツ変換で不変であるという事実より、
(Eq.14)
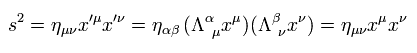
よって
(Eq.15)
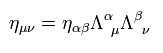
Eq.8 から
(Eq.16)
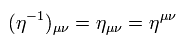
逆行列 × 行列は 次のように 計量テンソル行列、ローレンツ変換行列共に 単位行列になる。
(Eq.17)
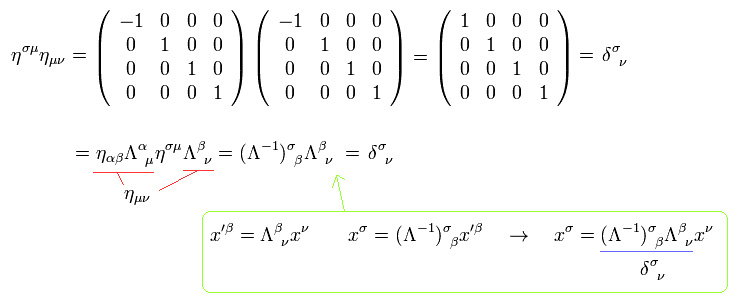
ここで Eq.15 を使った。
Eq.17 より ローレンツ変換の逆行列は、
(Eq.18)
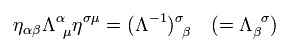
Eq.18 を用いて、 Eq.9 の共変ベクトルは ローレンツ変換で 次のように変化する。
(Eq.19)
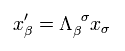
ここで Eq.19 を証明する。 Eq.18 を使うと、 Eq.19 は
(Eq.20)

Eq.9 と Eq.12 から、 η × 共変ベクトル = 反変ベクトル。
Eq.20 の両辺に ησ β をかけて、
(Eq.21)
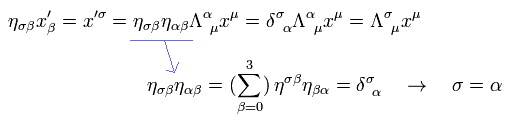
これは Eq.13 と同じである。結果的に Eq.19 は正しい。
Eq.18 から、共変ベクトルの変換 (= Eq.19 ) は 次のように表せる。
(Eq.21')
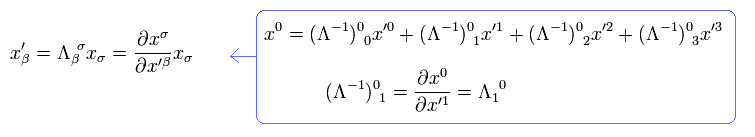
次に 偏微分演算子がローレンツ変換のもとで 共変ベクトルとして変換されることを示す。
(Eq.22)
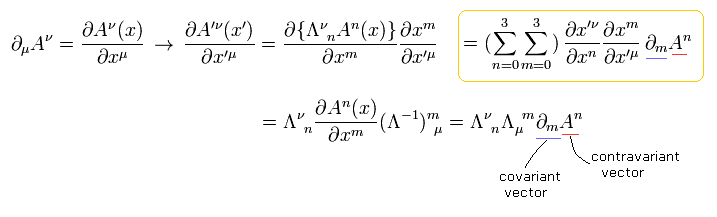
ここでは Eq.18 と Eq.13 の逆の関係式を使っている。
Eq.22 は ベクトル Aνの偏微分が いわゆる "テンソル"であることを示している。
Eq.22 では、 Aν は ローレンツ変換のもとで 反変ベクトルとして変化し、偏微分演算子は 共変ベクトルとして変化することを示している。
つまり 偏微分の添え字 (= μ) は Eq.22 では 下の位置にある。
基本的に 混合テンソルは ローレンツ変換のもとで 次のように変換する。
(Eq.23)
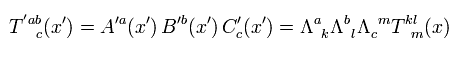
上で述べたように、相対論によれば 電磁気学は 正しく相対性理論に組み入れることに成功したことになっている。
しかし本当にそうだろうか?
一般相対論は 局所ローレンツ対称性に依存している。そのため 電磁場における特殊相対性理論が間違っていたとしたら 一般相対論も間違いということになる。
マクスウェル方程式は、
(Eq.24)
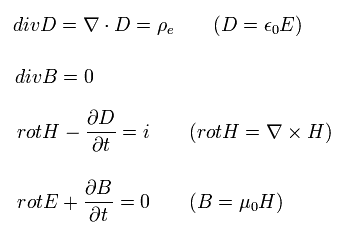
ここで E と H は それぞれ 電場と磁場を表している。
D と B は それぞれ 電束密度、磁束密度である。
このページでは 電流 i は Jμ ( μ = 1, 2, 3 ) とも表すことにする。
相対性理論では 電場、磁場は 次のベクトルポテンシャル (= A ) と スカラーポテンシャル (= φ)で表す。
(Eq.25)
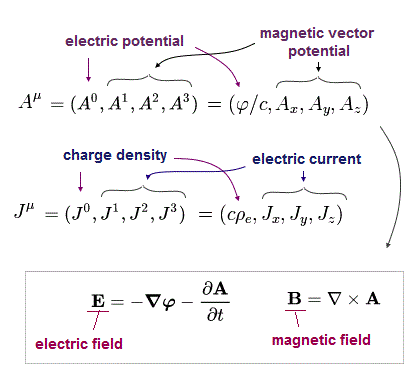
ここで ρe と J は それぞれ 電荷密度 と 電流密度である。
もし これらのベクトル、スカラーポテンシャル、電荷、電流密度を 相対論的な4元ベクトルとして定義しなかったとしたら、 電磁気学は 相対論を満たさない。
しかし これら Eq.25 の定義は 後で説明するが 観測者の単純移動による非常にミステリアスかつ奇妙な現象を引き起こしてしまうことになる。
相対論は電磁気学で破綻している。 も参照のこと。
(Eq.25-2) 4元ベクトル。

つまり これらの "人為的な" 4元ベクトルは Eq.4 のように変化する。
また 共変ベクトルは 上で述べたように ゼロ成分のみ マイナスになる。
(Eq.25-3)
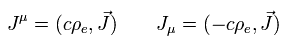
スカラーポテンシャルも φ/c = A0 = - A0。
ベクトル、スカラーポテンシャルを用いて 電場 (E) と 磁場 (B) を表すと、
(Eq.26)
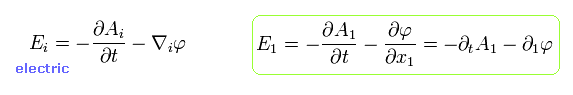
(Eq.27)
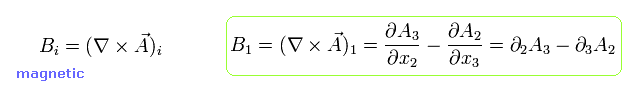
反対称テンソル ( Fμ ν ) を次のように定義する。
(Eq.28)
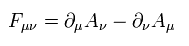
ここで A は ベクトルもしくはスカラーポテンシャルである。
空間座標 ( i = 1, 2, 3 ) の 偏微分記号は次のように書く。
(Eq.29)
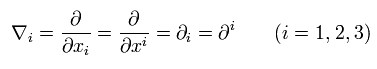
すでに述べたように、 Eq.29 の符号は添え字の位置で変化しない。
ゼロ成分 (= 時間 ) の偏微分記号は、
(Eq.30)
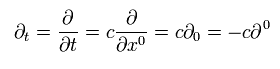
添え字 " 0 " が 上の位置にあるとき、時間微分は マイナスとなる。
なぜなら Eq.22 に述べたように 通常の偏微分は 共変ベクトルとして変換されるからである。
Eq.26、 Eq.27、Eq.28 より、 電場 (= E) と 磁場 (= B) は次のように表される。
(Eq.31)
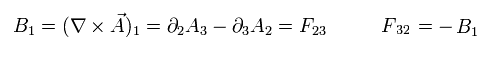
(Eq.32)
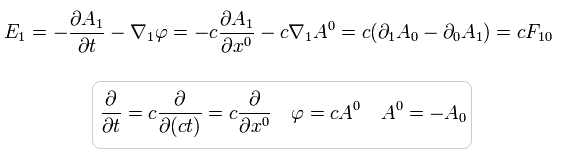
ここで A0 = - A0 = φ/c.
基本的に 電荷密度と電流密度 (= 電荷の流れ ) は 次を満足する必要がある。
(Eq.33)
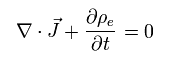
相対論によれば、観測者の動きに関係なく 電荷量は保存される。
つまり Eq.33 の式は ローレンツ不変でなければならない。
( もちろん "地球のエーテル" を認めれば 奇妙なローレンツ変換や4元ベクトルの概念を使用する必要はなくなる。 )
Eq.33 は 4元ベクトル ( xμ ) を使うと、
(Eq.34)
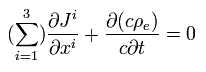
ct は x0 で置き換えられる。
ここで 4元ベクトル (= 4元電流密度 ) は、
(Eq.35)
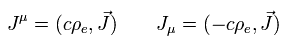
Eq.34 は次のように表せる。
(Eq.36)
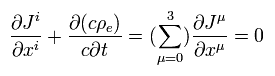
これは 反変ベクトル (= Jμ ) と 共変ベクトル (= 微分演算子 ) の組み合わせのため ローレンツ変換不変な スカラーになる。
ここで実際に Eq.36 がスカラーであることを示す。
ローレンツ変換のもとでは、 xμ による微分は、
(Eq.37)
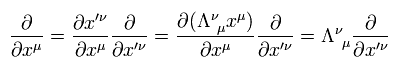
Eq.37 を Eq.36 に代入すると、次を得る。
(Eq.38)
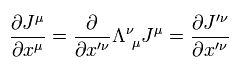
結果的に、Eq.36 (= Eq.33 ) は ローレンツ変換不変であることが証明された。
(Fig.6) 観測者 (= observer) の ”超能力”!
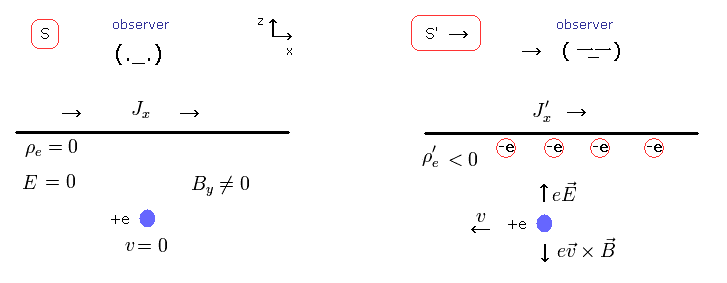
Fig.6 では、電流 Jx は 同数の プラスの陽子とマイナスの電子を含んでいる。
つまり この電流は定常かつ 中性である。(つまり 電荷密度 ρ はゼロである。)
Fig.6 の S 慣性系では、観測者と電荷 +e は静止している。つまり この電荷は いかなる外力を受けていない。( eE = evB = 0 )
しかし Fig.6 の S' 慣性系 (= 観測者が 一定の速度 v で右方向へ動いている ) から見ると、電荷 +e は 逆方向である左の方へ 速度 v で動いていることになる。
つまり この電荷 +e は 電流Jから 磁気的なローレンツ力 (= evB ) を受けることになる。
しかしこの場合は、電荷 +e は 観測者の運動に応じて 下向きに動いてしまうことになる。
この矛盾を回避するために、相対論は Eq.25 の 相対論的な4元ベクトルを定義したのである。
奇妙なことに、この理論によれば 何と 観測者の動きに応じて もともと中性の場所に マイナス電荷が自然発生してしまうのである!
( もちろん 上で述べたとおり もともとここに存在するプラスとマイナスの電荷量は等しくしてある。 )
Eq.25 の ベクトルポテンシャル、スカラーポテンシャル、電荷密度、電流密度は ローレンツ変換で Eq.6, Eq.7 ( Eq.25-2 ) のように変化する。なぜなら それらは4元ベクトルだからである。
(Eq.39)
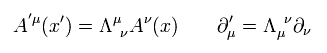
定常電流 J は 中性で かつ x 方向である ( Fig.6 の左 )。 つまり 電荷と電流密度は、
(Eq.40)
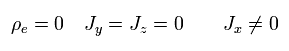
結果的に y 方向の磁場 ( By > 0 ) が生成される。 ( 電場 E はゼロである。)
(Eq.41)
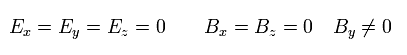
Eq.26、 Eq.27、 Eq.39 を使うと、 右方向へ動いている観測者から見る電磁場は ( S'、 Fig.6 の右図 )、
(Eq.42)
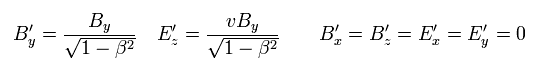
ここで Eq.42 を証明する。
Eq.40 より、 電流 J は x 方向のみで、定常かつ一様とする。 すると ベクトルポテンシャル A は、
(Eq.42-2)
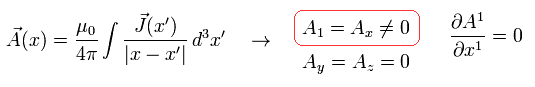
A0= ( φ/c ) = A2 = A3 = 0、 Eq.25-2、 Eq.42-2、 と ローレンツ変換の逆 ( Eq.4 で -v を +v に変える ) 考慮すると、
x 方向の電場は ローレンツ変換で次のように変化する。
(Eq.42-3)
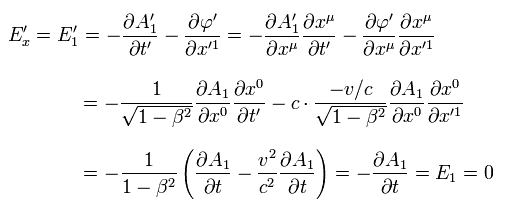
ここで x0 = ct と β = v/c である。
Eq.42-3 は 電場 Ex は ローレンツ変換で変わらない (= 0) ことを示している。
磁場の場合は、
(Eq.42-4)
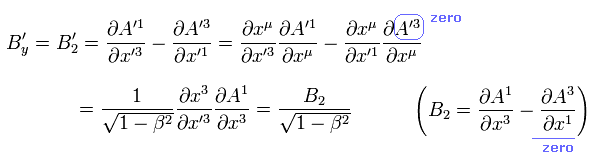
同様に Eq.42 を示すことができる。
結果的に 観測者が動いているときでさえ、電荷 +e は z 方向 ( もしくは y 方向 ) へ動かないことになる。 なぜなら ローレンツ力 (= evB ) が 電場による力 (= eE ) に等しくなるからである。
(Eq.43)
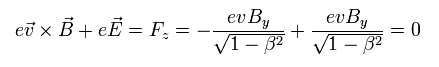
しかし もともとマイナスとプラスの電荷量がまったく等しい中性のところに なぜ 電場 (= E ) が生じてしまったのだろうか??
トリックは Eq.25 の 電荷と電流密度の4元ベクトルの関係にある。
動いている観測者から見ると、これらは次のように見えることになる。
(Eq.44)
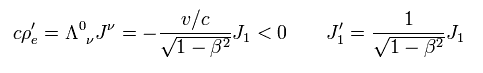
驚くことに Eq.44 は 観測者が 電流に対して何もしていないのに マイナスの電荷が自然発生してしまったことを意味している!
(Fig.7) 観測者の "見る力" が電荷を自然発生させた ??
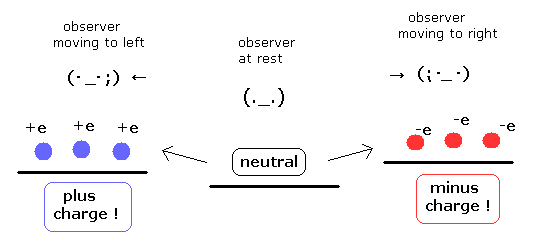
Fig.7 に示すように、中性の電流は 観測者の動きの向きに応じて マイナスかプラスの電荷を自然発生することができるのである。
これは非常に奇妙である。
( すでに述べたように これは ローレンツ変換そのものが原因である。)
基本的に 中性電流 i は 次のように プラスとマイナスの電荷の相対運動である。
(Fig.8) 中性の電荷は中性のままである!
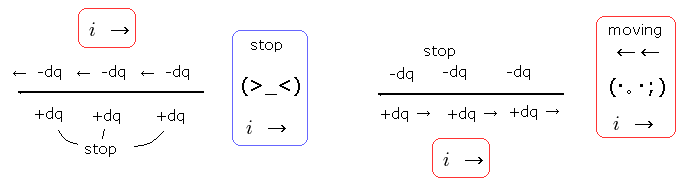
そこに何も与えなかったら 中性の電荷が中性のままであることはあたりまえの話である。
これが 相対論的な電磁気学における 最も重要なトリックである。
もし これらの奇妙な現象を否定したとしたら、それは 特殊(かつ 一般)相対性理論と QED が間違いということになる。
通常の教科書によれば、動いている観測者の視点からは 電線が収縮して見える (= ローレンツ収縮 )。
また Eq.7 の ローレンツ変換のもとでは、電荷密度 ρ が大きくなる。 ( 電荷密度は 4元ベクトルの1つである。)
結果として、全電荷 = 電荷密度 × 電線の長さ は ローレンツ変換で 変化しないことになる。
しかし この説明は Eq.44 の定義と一致しない。
通常の教科書は プラスかマイナスの電荷 片方のみの視点でしか説明していないのである。
このコメントが本当なら、ローレンツ変換で プラスとマイナスの電荷密度 両方とも 大きくなることになる。なぜなら 両方の電荷とも 同一の ローレンツ収縮した電線の中にあるからである。
Eq.44 では、マイナスの電荷密度のみ増加している。両方の電荷とも 同一の電線内にあるにも関わらずだ。
つまり、相対論的な電磁気学は 完全に 電荷の保存則を破っていることになる。
相対論は電磁気学で破綻している。 も参照のこと。
-----------------------------------------------------------------------------------------
(Fig.W-1) 電線のループは回転する?それともしない?
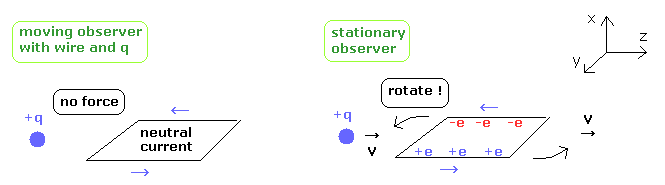
最近の興味深い報告によれば、何と ローレンツ力が特殊相対論と一致しないらしい。
( Masud Mansuripur, Trouble with the Lorentz law of Force: Incompatibility with Special Relativity and Momentum Conservation. Phys.Rev.Lett 108, 193901, 2012.)
この論文は z-y 平面上の 電流の流れているループのうち、z 方向の2つの電線における 上記の全電荷の保存則の破れを用いているようである。
Eq.44 に示したように、静止した (= stationary) 観測者からの視点では 電気的に中性な電流のループ線に突如として プラスもしくはマイナスの電荷が発生することになる。
(この論文では、電線と電荷 q は z 方向に速度 v で動いている。そのため 静止した観測者からは 電線は z 方向に動いている。)
このループ線中の z 方向の2本の電線の電流の流れは 互いに逆方向であるため、これらは互いに逆の電荷密度 ( + もしくは - ) を生じさせる。
そのため、静止した観測者から見たら、もう1つの電荷 q が この電荷双極子を回転させることになる。
ところが、この電線と電荷 q と伴に動いている観測者からしたら、もちろんそれは回転することはない。
これは 明らかにパラドックスである。実は 相対論は Eq.43 のローレンツ力の関係式が成り立つ方向以外には対応できないのである。
これを解決するには まったく別の仮想の回転中心をこしらえたりするしかない。
つまり このパラドックスは 解決されていないのである。
( 隠れた電磁場の運動量はこのパラドックスを解決できたか も参照のこと。 )
-------------------------------------------------------------------------------------------
Eq.24 から 真空の電磁場エネルギーを導くことができる。
( このページも参照のこと。 )
E と Eq.24 の3番目の式の内積 と H と Eq.24 の4番目の式の内積は、
(Eq.45)
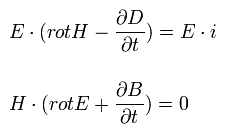
Eq.45 で 上の式 引く 下の式は、
(Eq.46)
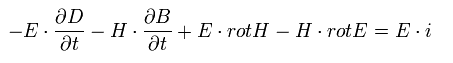
次の公式を使うと、
(Eq.47)
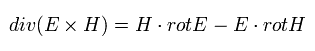
また次の関係式、
(Eq.48)
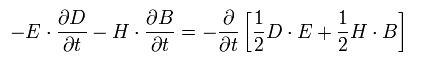
かつ次の定義も使うと、
(Eq.49)
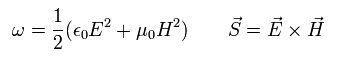
次を得る。 ( 真空で 電流密度 i = 0 )
(Eq.50)
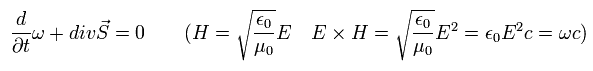
そのため彼らは Eq.50 は 電磁場のエネルギー (= ω ) と その流れ ( S = ポインティングベクトル ) の関係式だと主張しているのである。
しかし このページに示したように、単一電子 (もしくは陽子) の周囲の電磁場のエネルギー は Eq.49 の ω で表せない。
なぜなら Eq.49 の電場のエネルギーは 単一電子に含まれる無限小電荷 (= dq ) 間の位置エネルギーを意味しているからである。
しかし 単一電子はそれ以上分解できないし、 かつ それよりも小さな無限小電荷より形成されているわけでもない。
(Fig.9) 単一電子 -e = -dq -dq -dq -dq ... ?
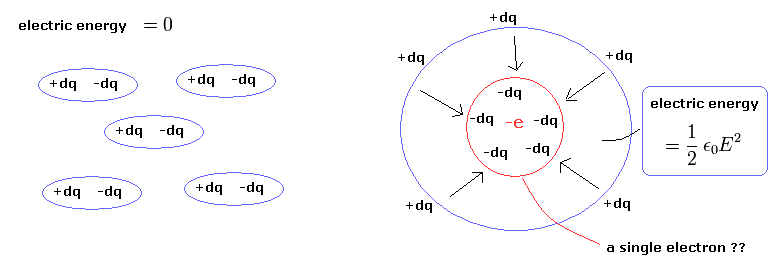
これは ボーアの電子がエネルギー放射するという誤解の要因である。
実は 特殊 (かつ 一般) 相対論は Eq.49 の真空の電磁場エネルギーに完全に依存している。
( もし Eq.49 の ω がエネルギーを意味しないとしたら、 相対性理論 ( と QED ) は 相対論的なエネルギー・運動量テンソルを満足しなくなる。 )
エネルギー・運動量テンソルという概念は 重力や一般相対論にとって 非常に重要な概念である。
Eq.51 から Eq.70 は このページの最後の章に移動した。
上で述べたように、特殊相対論は 電磁場のように重力を説明することができなかった。
( しかし 相対論的な電磁気学は 上で述べたような非常に奇妙な4元ベクトルに依存しているが・・・)
そのため 重力のみによって影響を受ける時空間について考える必要がある。
( これはつまり、重力を消し去ることができたとしたら、この時空間は ローレンツ変換のミンコフスキー時空間と等しくなることを意味する。 )
重力を消し去るには、Fig.4 右図で示したように、我々観測者が重力に従って落下しなければならない。(= 自由落下 )
( これを 局所慣性系と呼び、ここでは 特殊相対論が有効である。)
重力のある環境で、静止した観測者 (= 落下してない) の視点からの スカラーである距離は
(Eq.71)
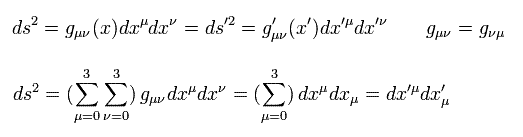
ここでは Eq.79 の定義を用いた。
このスカラーの距離は Eq.3 のミンコフスキー時空間のものと一致しなければならない。
これはつまり、 gμν(x) (= "一般化された" 計量テンソル ) は リーマン空間とミンコフスキー空間の "連結" に関係していることを意味している。
もちろん、この連結は重力と関係していることは言うまでもない。
Fig.4 右図に示したように 観測者が重力に従って落下している視点からでは この gμν は Eq.8 のミンコフスキーの計量テンソルに等しくなる。
これらの 共通のスカラーの定義や 重力を観測者で消去するシステムは 完全に人為的な定義であることを肝に銘じておく必要がある。
そして この一般相対論における スカラーを用いた非常に厳しい制限が 超弦理論などを 物理というより 単なる抽象的な数学上の概念にしている根源である。
加速を含む一般座標変換は、
(Eq.72)
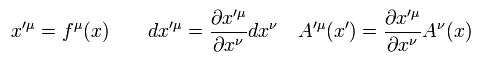
Eq.72 は 反変ベクトルの一般座標変換である (Eq.13 も参照のこと)。
知ってのとおり、特殊相対論では この変換は Eq.4 のようにならなければならない。 これは加速を含んでいない。
この変換が加速のとき、 f(x) は 2回微分可能となる。
( ローレンツ変換の Eq.6 は 1階微分可能である。 この場合は 偏微分は Eq.7 の Λ となる。 )
目指すものは Fig.4 右図に示したように、重力の方向へ加速することによって ミンコフスキー時空間へ移ることである。
もしミンコフスキー時空間へ移らないと 一般相対論そのものは無意味なものとなってしまう。
リーマン時空間の偏微分導関数は (ミンコフスキー時空間と同じように )、
(Eq.73)
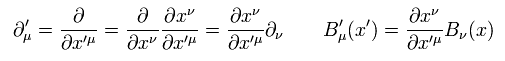
Eq.73 は 一般化された共変ベクトルである。
Eq.21' も参照のこと。
Eq.14 のように、 Eq.72 を Eq.71 に代入すると、次を得る。
(Eq.74)
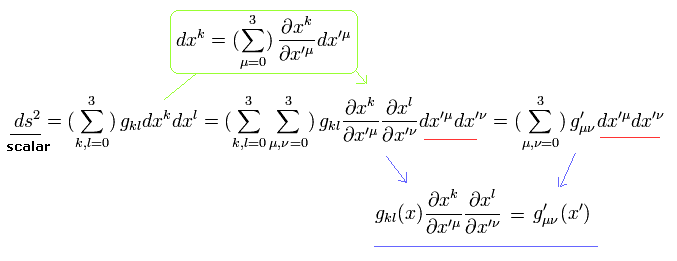
つまり 計量テンソル g は 2階のテンソルとして変化する。
( これが "テンソル" と呼ばれる所以である。 )
Eq.72 の一般座標変換によって ミンコフスキー時空間へ移行すると、次のように この計量テンソルは (局所的に) ミンコフスキー計量テンソルになる。
(Eq.75)
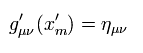
すでに述べたように この定義は 重力が観測者によって消去できるという 人為的な前提に基づいている。
Eq.74 と Eq.75 より、 各行列式を考慮して、 (= 行列式 × 行列式 × ... ),
(Eq.76)
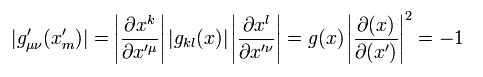
ここでは ミンコフスキー計量テンソルの行列式 = -1 ( Eq.8 ) を用いた。
そのため 一般化した計量テンソルの行列式 g(x) は 次のようにマイナスとなる。
(Eq.77)
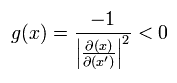
また 次のように gμν を定義する。
(Eq.78)
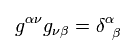
一般的に Eq.8 のミンコフスキーの計量テンソルと違い、 gμν は gμν に等しくない。
また Eq.78 は次を満たす。
(Eq.79)
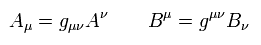
ここで Aν と Bμ は 反変ベクトルであり、 Aμ と Bν は 共変ベクトルである。
Eq.79 は 次によって確かめられる。
(Eq.80)
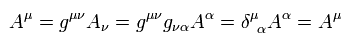
リーマン,リッチ,アインシュタインテンソルの導出 (12/9/29) のページで、 次の重要な関係式を得た。
(R-1) 共変ベクトルの平行移動。
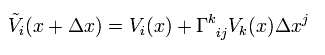
(R-2) 反変ベクトルの平行移動。
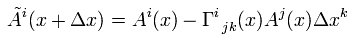
(R-3) 計量テンソルによるクリストッフェル記号 -1。
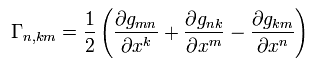
(R-4) 計量テンソルによるクリストッフェル記号 -2。
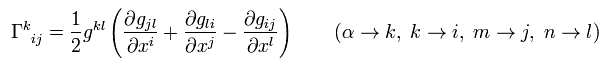
(R-5) クリストッフェル記号の一般座標変換。
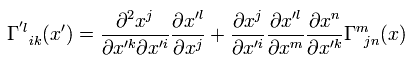
(R-6) 共変ベクトルの共変微分。
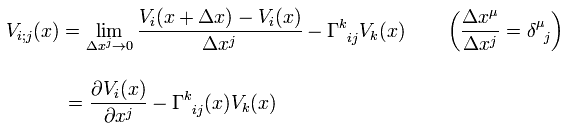
(R-7) 反変ベクトルの共変微分。
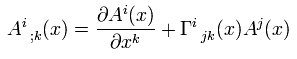
(R-8) リーマン曲率テンソル。
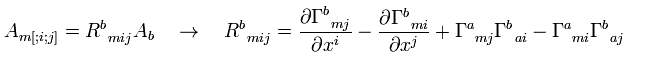
(R-9) リーマン曲率テンソルの対称性。
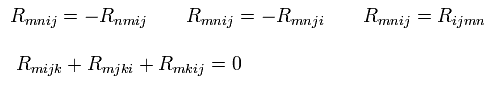
(R-10) リッチテンソル。
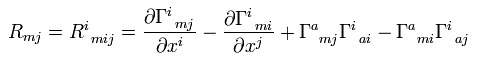
(R-11) スカラー曲率。
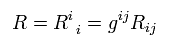
(R-12) ビアンキの恒等式。
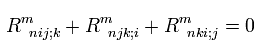
(R-13) アインシュタインテンソル。

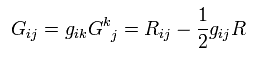
(R-14) アインシュタインテンソルによるリッチテンソル。
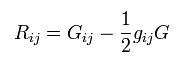
もしまだ リーマン幾何学 を読んでいなければ最初にそちらを読むように。
相対論によれば、異なった慣性系からの 速度 (= u(t) ) は異なる。
(Eq.81)
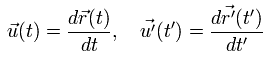
そのため dt の代わりに、次の固有時 (= τ ) を使うと、
(Eq.82)
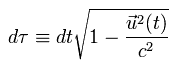
とても便利である。 ( このページも参照のこと。 )
なぜなら この固有時は 運動する物体とともに動く系のものと定義されたもので、次のように ローレンツ変換不変な スカラー値だからである。
(Eq.83)
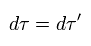
Eq.81 の代わりに、 次の4元速度 (= ω )を使う。これらは ローレンツ変換のもとで 4元ベクトルとして変化する。
(Eq.84)
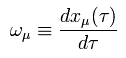
慣性系における自由粒子のラグランジアンは 次のように表せる。 ( Eq.82 を使って )
(Eq.85)
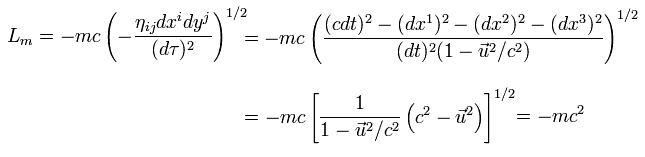
Eq.85 のラグランジアンはローレンツ変換不変なスカラーであるため、運動方程式はすべての慣性系で有効となる。.
作用 S の極小を考えると、 運動方程式を意味するオイラー・ラグランシュ方程式を得る。
(Eq.86)
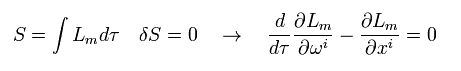
Eq.84、 Eq.85、 Eq.86 から、 次の自由粒子の運動方程式を得る。
(Eq.87)

例えば、 その 1 成分は、
(Eq.87-2)
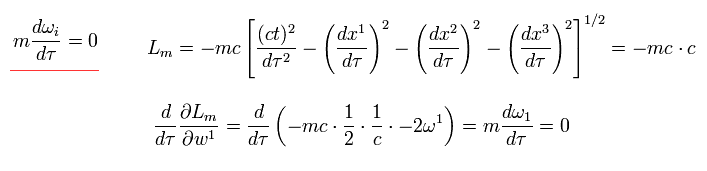
Eq.85 のように、 Eq.71 の計量テンソルを用いて、重力のみのもとでの (自由)粒子を定義できる。
(Eq.88)
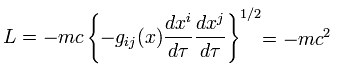
ここで
(Eq.89)
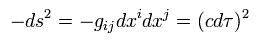
そのため 重力のもとでの Eq.88 のラグランジアン (= -mc2 ) は Eq.85 に等しくなる。
Eq.88 における 作用の変分は、
(Eq.90)
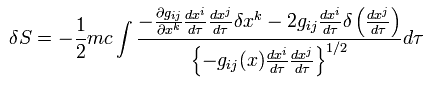
ここで 分子の2項目は、
(Eq.91)
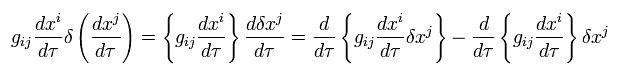
Eq.88 から、Eq.90 の分母は c、 よって Eq.90 は、
(Eq.92)
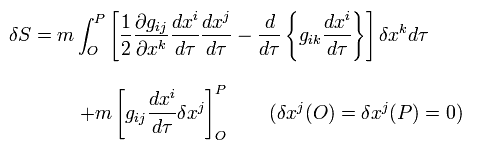
ここで 2行目はゼロである。
また Eq.92 の2項目は、
(Eq.93)
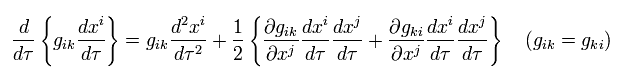
ここで 2項目を 2つに分離した。
Eq.93 を Eq.92 に代入して、 その変分がゼロのとき、
(Eq.94)
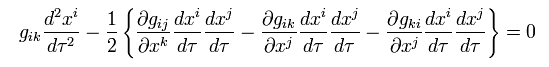
Eq.94 に gmk をかけると、最初の項は、
(Eq.95)
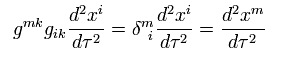
R-4 (= クリストッフェル記号 ) を使うと、Eq.94 の他の項は、
(Eq.96)
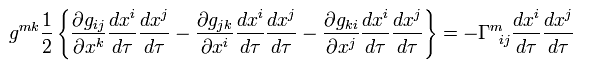
Eq.94、 Eq.95、 Eq.96 から、 重力のみのときの運動方程式を得る。
(Eq.97)
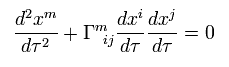
ここで 2項目は重力による加速度 (= g) を表している。
つまりすでに述べたように、クリストッフェル記号 ( これは一般化された計量テンソル gμν から構成される ) は重力と関係している。
Eq.84 の4元速度 ω を用いると、 Eq.97 は、
(Eq.98)
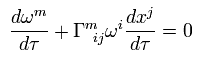
よって、
(Eq.99)
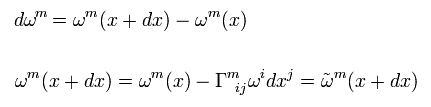
R-2 を使うと、 重力だけのもとでの 4元ベクトル ω は 平行移動することになる。
つまりすでに述べたように、平行移動は 重力のみによる粒子の動きを意味している。
実際のところ、重力場が少し複雑だと、重力のもとでの運動方程式を得ることは 非現実的なくらい難しくなる。
そのため 一種の近似を使わなければならない (= 非常に弱い静的な重力場のもとでの )。
( しかし この一般相対論における近似は あまりにも多くを省きすぎている気がするが・・)
そのため この弱い重力のもとでは、 計量テンソルは 次のようにほとんどミンコフスキー η と同じになる。
(Eq.100)

また この計量テンソルが時間に依存しない (= static ) と仮定する。
(Eq.101)
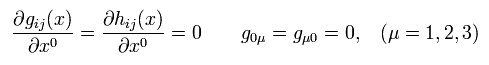
また gμ 0 ( μ = 1, 2, 3 ) はすべてゼロとする。
さらに 粒子の速度 (= ωμ, μ = 1, 2, 3 ) が非常にゆっくりしているとする。
(Eq.102)
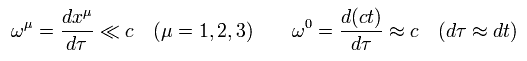
微小量の2次の効果を無視して ( 例えば h(x) × h(x) )、 Eq.100 を使うと、R-4 のクリストッフェル記号は、
(Eq.103)
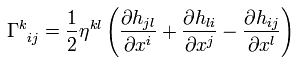
Eq.103 を 重力のもとでの運動方程式 (= Eq.97 ) に代入して、速度が無限小であることを考慮すると、
(Eq.104)
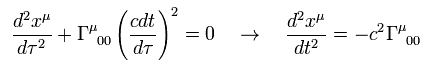
Eq.102 に示したように、 ωμ × ωμ (μ = 1, 2, 3) は近似的にゼロである。
Eq.101 と Eq.103 を考慮すると、
(Eq.105)
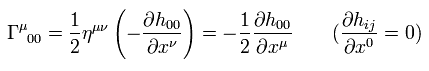
ここで μ は ゼロではいけない。
Eq.104 と Eq.105 から、次を得る。
(Eq.106)
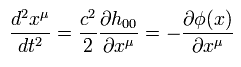
ここで φ(x) は、 重力場のポテンシャルである。
Eq.106 より、 h00 と g00 は 重力場のポテンシャルを用いて 次のように表せる。
(Eq.107)
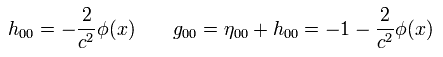
Eq.69 の電磁場のケースのように、重力の場合にも エネルギー運動量テンソルを導入する。
( そのため 電磁場のエネルギー・運動量テンソルが無意味だと、重力でも無意味となる。)
R-13 のアインシュタインテンソルを エネルギー運動量テンソルとして使用すると、 この方程式は アインシュタインの重力場方程式と呼ぶ。
(Eq.108)
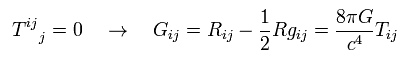
エネルギー密度 T00 は 質量エネルギー密度を意味しているので、
(Eq.109)
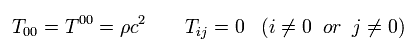
ここで ρ は質量密度である。
ここで Eq.106 が Eq.108 の非常に弱いかつ静的な重力場の状況のときにも成り立つか確認する。
Eq.108 に gij をかけて、
(Eq.110)
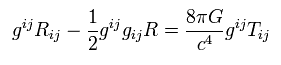
次の定義を使い、
(Eq.111)
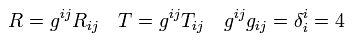
(ここで Eq.78 を使った。)
Eq.111 を Eq.110 に代入して、 108 を使うと、
(Eq.112)
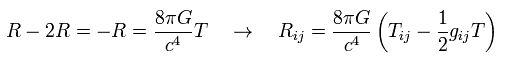
Eq.78 から、 無限小の計量テンソルは次のように表せる。
(Eq.113)
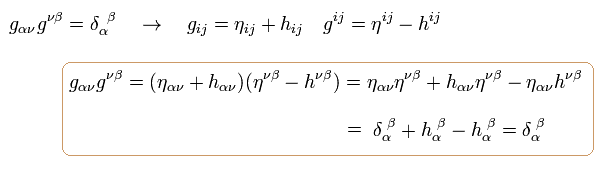
静的な真空では、 すべての Tμν ( T00 を除く ) はゼロになるため、
(Eq.114)
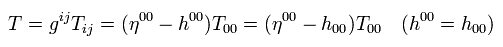
Eq.114 を Eq.112 の R00 に代入して、
(Eq.115)
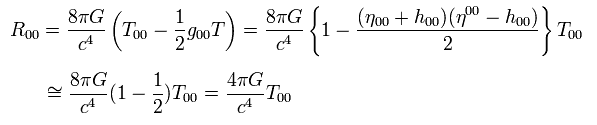
ここで η00 × η00= 1 を使い、 2次の無限小値を無視した。
R-10 の リッチテンソルを使うと、,
(Eq.116)
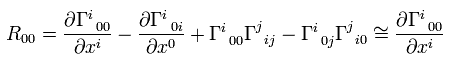
ここで Eq.101 と Eq.103 を用いて、 2次の無限小値を無視した。
Eq.103 と Eq.116 から、
(Eq.117)
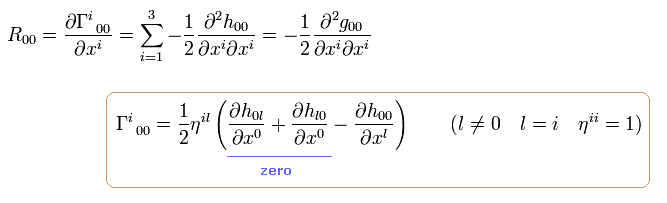
Eq.107、 Eq.109、 Eq.115、 Eq.117 から 次を得る。
(Eq.118)
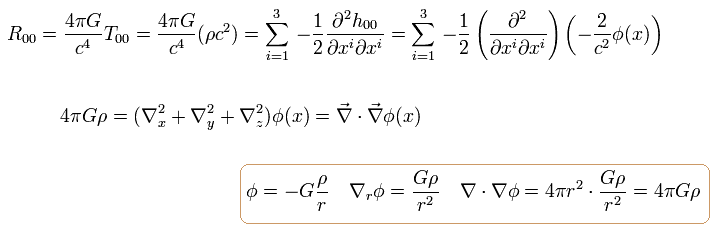
Eq.118 は ニュートン力学の重力に等しい。
ニュートン力学の重力と合うように、 Eq.108 のアインシュタインの重力場方程式を選んだのである。
そのため アインシュタインの重力とニュートンの重力が等しいことはしごくあたりまえのことである。
また このページに示したように、一般相対論の近似は あまりにも省きすぎである。
これだけ省いた近似で わずかな差を示すことが果たして信頼性を示せるのか疑問である。
計量テンソル g の共変微分がゼロであることを考慮して、 ( このページ の Eq.51 を参照のこと。 ) Eq.108 に次のような別の項を追加できる。
(Eq.119)
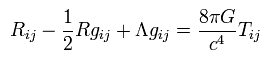
この Λ を "宇宙項" もしくは "宇宙定数" という。
しかし、Eq.119 は ニュートン力学の Eq.118 と一致しない。
そのため 宇宙項が非常に小さいときのみ、 Eq.119 を使うことができる。
シュバルツシルト解 (計量) は 1915 年の アインシュタイン方程式の最初の解であり、 ブラックホールの存在を予言した。
( しかし、ブラックホールは直接的には発見されていない。 )
このケースでは 質量 M の点粒子が 原点にあり、 重力場は球対称であり かつ静的としている。
( そのため シュバルツシルトの計量は 最初から地球のようなものを想定していた。 )
極座標を用いて、
(Eq.120)
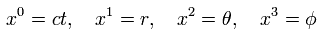
詳細な計算は シュヴァルツシルト解 と GPS のパラドックス を参照のこと。
重要なのは時間成分であろう。
Eq.107 から、重力場のポテンシャル φ(r) = -GM/r (= ニュートン力学 ! ) である。
(Eq.124)
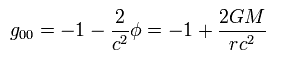
つまり、
(Eq.125)
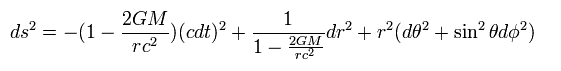
Eq.125 から、 半径 r が次より小さいとき、
(Eq.126)
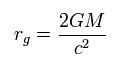
g00 はプラスになってしまい、space-like を意味する。
Eq.126 の半径を シュバルツシルト半径と呼び、 "ブラックホール" に関係している。
要するに ブラックホールは 相対論的な因果律に矛盾しているのである。
しかし 彼らは 一般相対論をあきらめなかった。なぜなのだろうか?
もちろん、アインシュタイン自身は ブラックホールの存在を信じていなかった。
相対論をあきらめることは すなわち 相対論的なディラック方程式を 何か別のもので置き換えなければならないことを意味している。
そのため結局 因果律に反する結果が出ても 諦められなかったのである。
これが 相対論に反する奇妙なブラックホールが生き残ったメインの理由である。
Eq.89 から、 固有時は、
(Eq.127)
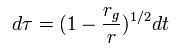
ここで dt は無限遠 (= 重力がゼロ ) での時間である。
Eq.127 は 重力が強くなるほど、時間が遅れる ことを意味する。 しかし この現実の世界で はたしてそんなことが起こり得るのだろうか??
Fig.10 は 簡単にイメージしたものである。
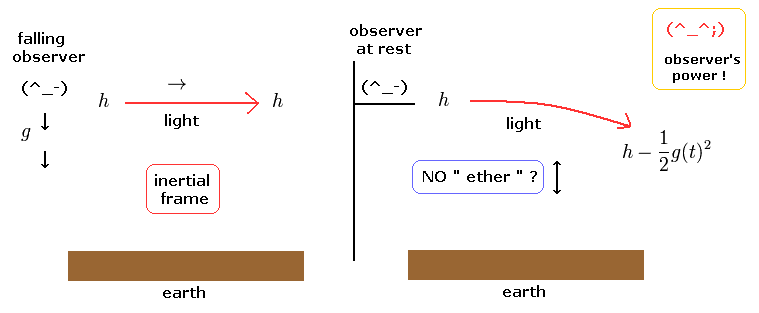
観測者が重力によって落下しているとき、 光はミンコフスキー空間のようにふるまう ( Fig.10 の左図 )。
これはつまり、観測者が地球に対して静止しているとき、 光は 1/2 gt2 地球のほうへ曲がることを意味している。光に質量がないにも関わらずだ。
よって 地球に近付くほど (= 重力が強くなるにつれ )、 時間が遅れて 光はゆっくり進み、これによって光を地球方向へ曲げるというわけだ。
しかし この説明にはいくつか奇妙な点がある。
最初に、Fig.4 で述べたように、たとえ観測者が地球方向へ落ちていようとも、対象へ作用する 重力はなくなっていない。
つまり 観測者の”見る力” が超能力のようで、Fig.7 の 観測者が ただ見るだけで 電荷を生じさせるのと似ている。
結論から言って、相対性理論においては観測者の存在は特別すぎるのである。これは量子力学に似ている。
それに Fig.4 に示すように もともと質量のある物体にたいして慣性系を定義したのに、いつの間にか質量ゼロの光に問題がすり替わってしまっている。
また、相対論においては エーテルが禁止されている。そのため 真空に何も含んでいないのに どうして ゼロ質量の光が重力によって 曲げられるのだろうか?
これは非常に奇妙である。
(Fig.11) " 地球のエーテル " による一般相対論。
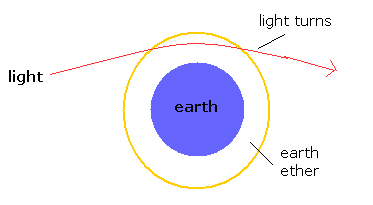
このページで述べたように、もし我々が 地球に引きつけられる 地球エーテル を認めたら、マイケルソン・モーリーの実験を説明できる。.
同じように エーテル (= 光の媒質 ) が地球に引きつけられたとき、光が地球方向へ曲がると考えることは極めて妥当である。
もしくは 地球へ近いほど 誘電体があることを考慮すると、地球へ近づくほど 光の速度が遅くなり 地球のほうへ曲がると考えることもできる。
時間が遅れると、電磁波の周期が長くなりかつ 光の振動数が小さくなると言われている。
そのため、彼らは 光が 星の重力場から放射されるとき、星から遠くの地点で観測すると、その波長が長く (= 赤方偏移 ) なると主張しているのである。
しかし 時間や時計のすすみの遅れなんて本当に起こっているのだろうか??
すでに述べたように、光の媒質であるエーテルが 重力のほうへ引きつけられてるとしたら、光が星に近くなるほど それはそこに留まりやすくなる。
( 結果的に 星から放射される光の波長は 引き伸ばされる。)
もちろん、星に近付くほど 誘電体があることを考慮して、速度が遅いところから速いところへ放射されれば 波長は引き伸ばされるだろう。
もしくは、重力の引きつけによる 光のエネルギーロスなども考慮して それが振動数に影響を与えるとも考えられる。
”便利な 光子”は 様々な物質で満たされた宇宙を”無傷”で通り抜けられるのか?
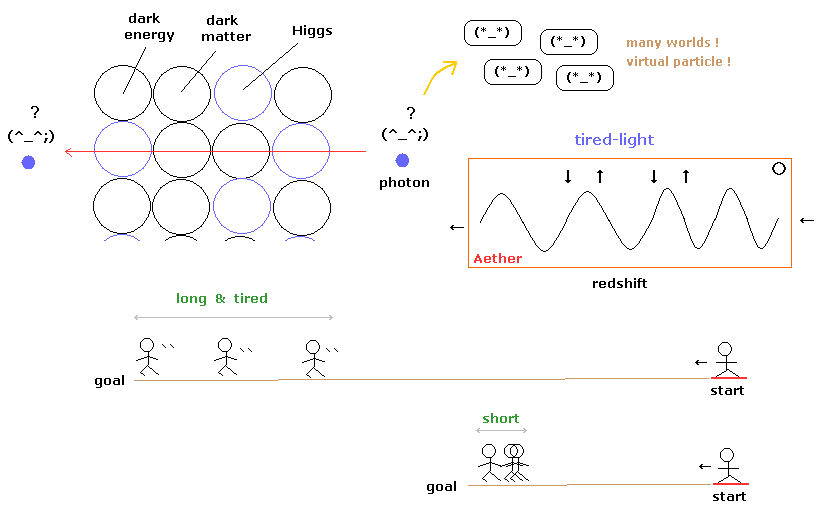
実際には 重力は弱すぎるのである。
そのため 星レベルの実験となり、容易に他のいろんな要因の影響を受ける。
例えば、衛星の時間に与えると言われる重力の効果は 1日でたったの 38 マイクロ秒である。
”時間、時計の遅れ”のような奇妙な考えは 実験結果を説明するとき 最も後回しにすべきことであろう。
一般の教科書には よく 様々な実験によって一般相対論の正当性が証明されたと書かれている。
しかし実際には それは一部にすぎない。
例えば 銀河全体の回転などは 一般相対論ではまったく対応できない。
なぜなら たとえ銀河全体に含まれているすべての質量を考慮しても 銀河の回転に必要なエネルギーに到達できないからである。
(Fig.12) ダークマターは ”宇宙空間のエーテルの回転”である。
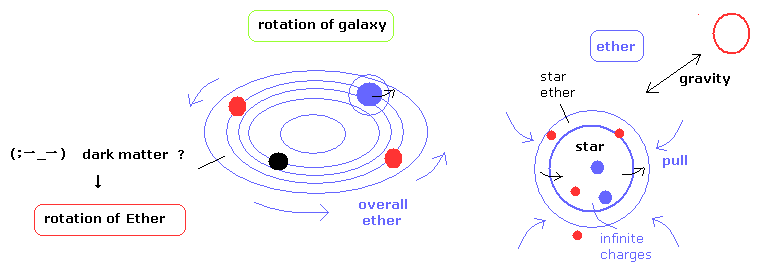
これはつまり 一般相対性理論が破綻していることを意味している。
この欠陥を穴埋めするために 奇妙なダークマター (暗黒物質) なるものが導入されたのである。
このダークマター (とダークエネルギー) は 宇宙の大半 を占めるといわれているが、まったく実態が分かっていない謎のものである。
もし エーテル を認めたとしたら、これらの現象を容易に説明することができる。
( もちろん これをするには、上で述べたように ディラック方程式から ボーア・ゾンマーフェルト模型に戻る必要がある。)
すると、銀河全体の回転は 宇宙空間のエーテルの回転によって生じると解釈される。( コップの中に含まれている水全体が回転しているのを思い浮かべるといい。)
星 (地球) は 互いに媒質 (= エーテル) を介して引きあっている無限の電荷集団から成り立っており、それらが一緒に動いていることは自然なことである。
一般的に 物はより安定化しようとし、無限のプラスとマイナスの電荷集団は互いに引き合って安定になろうとする過程で 周囲のエーテルを引きこむ形となる (= 星のエーテル )。
例えば、空中を飛行している飛行機の中の空気は 飛行機といっしょに動いている。
これが 宇宙と地球 (= 星) のエーテルの運動であると推察される。
また 宇宙空間における 大量の電荷 (= 質量) の 不均衡が 宇宙空間のエーテルを介した重力を生じると考えられる。
( また "ニュートリノ" は エーテル中を伝わる ドブロイの縦波と考えるのが自然である。)
---------------------------------------------------------------------
最近の興味深い報告では 重力は実は存在しない というのがある。
( Erik Verlinde, On the origin of gravity and the laws of Newton, Journal of high energy physics, 2011, 4, 29. )
重力の非常に弱いことを考えると、重力は クーロン力なども含む様々な要因の総合的なものと考えるのが自然と言える。

2012/4/12 updated This site is link free.