
( xμ、 pμ、kμ は 4元ベクトルである。 )
トップページ (2電子原子も含む正確な新ボーア模型)
QED の g因子のページに戻る。
場の量子論のページに戻る。
このホームページでは、(-1, +1, +1, +1) バージョンの計量テンソルを使用している。
つまり、4元ベクトルのゼロ成分のみ 添え字の位置によって変化する。
もし、(+1, -1, -1, -1) バージョンの計量テンソルに変換したいときは、Eq.1, Eq.2 に示すようにするといい。
(Eq.1)

( xμ、 pμ、kμ は 4元ベクトルである。 )
また、行列は、
(Eq.2)
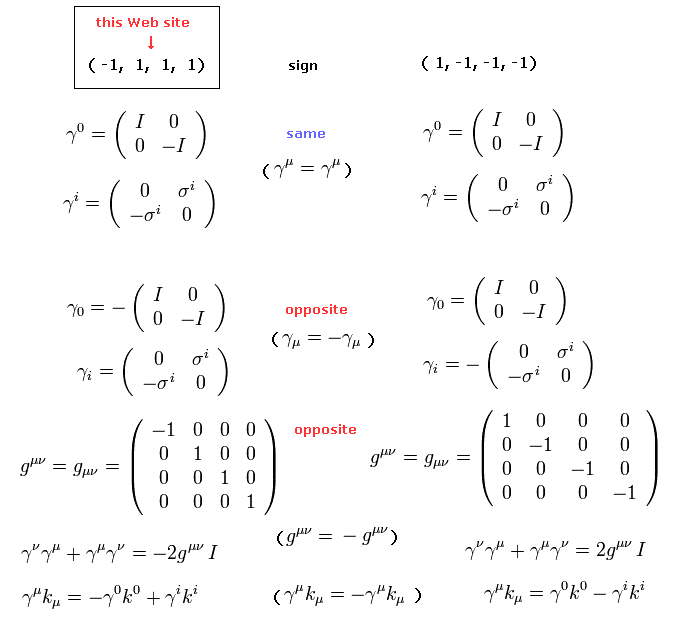
基本的に、式の意味は、両バージョンで まったく同じである。
表記の仕方のみが違うだけである。
要するに、もしバージョンを変更したいときは、適切な箇所で 符号を ( + → -, もしくは - → +) のように変更するとよい。
ここで、このページの Eq.85 の式の変換を証明する。
(Eq.3) = (Eq.85)
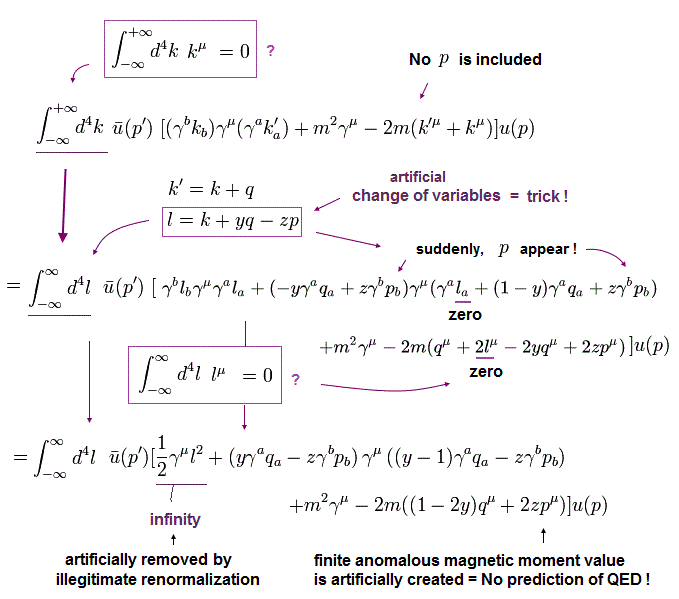
ここでは
(Eq.4)
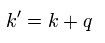
Eq.4 では、 "q" は 光子、 "p" は 電子、 "k" は 電子の伝播関数である。
ここで このページの Eq.80 の "l" を使用する。
(Eq.5)
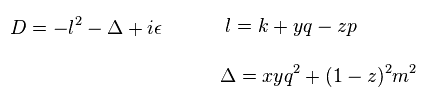
Eq.5 を使うと、 Eq.3 の最後の項 (3行目) は 次のように表せる。
(Eq.6)
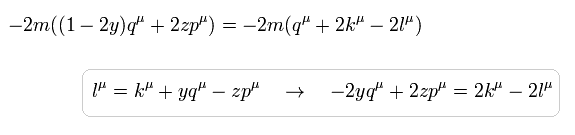
このページ (Eq.80) に示したように、分母 D3 は l2 を含んでいる。
つまり、分母は l の偶関数である。
これは つまり、分子が奇関数のとき、積分は次のようにゼロになる。
(Eq.7)
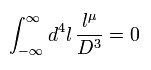
実際に Eq.7 は 無限大の力を利用している。
新しい変数 l は k を 有限量 シフトさせて作ったものであることを忘れてはいけない。(Eq.5 を参照のこと。)
もし 積分変数 k が -∞ から +∞ でなければ この l は 偶関数にも奇関数にもなれない。
つまり Eq.7 の便利な道具は 無限大に依存している。
Eq.7 を使うと、Eq.6 の最後の項は ゼロになる。そのため Eq.3 の3行目は,
(Eq.8)
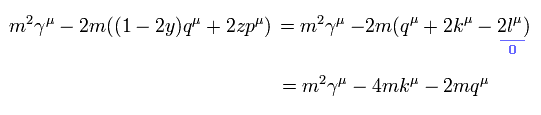 <
<
Eq.4 を使うと、 Eq.3 の 1行目は、
(Eq.9)
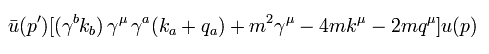
結果的に Eq.8 は Eq.9 の最後の3つの項に等しい。
お気づきかもしれないが、 この QED の手法は このページの Eq.10' と Eq.10'' に示すように 間違った数学である。
Eq.5 を用いると、Eq.3 (2行目) の2項目は、
(Eq.10)
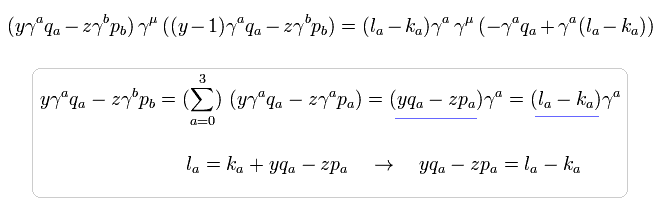
Eq.10 (右辺) の中の 1つの項は 次のように表せる。 (ここで 左側の添え字 a を b に変更している。)
(Eq.11)
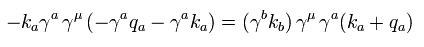
つまり、 Eq.11 は Eq.9 の残りの項に等しくなる。
要するに、Eq.3 (2行目) の残りの項はゼロにならなければならない。
( これらの "ゼロ"の項は 意図的につけられた。)
Eq.10 の別の項は、
(Eq.12)
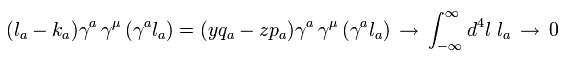
Eq.12 は l の奇関数のため、積分するとゼロになる。
同様に Eq.10 の次の項もゼロになる。
(Eq.13)
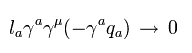
Eq.10 に最後に残った項は、
(Eq.14)
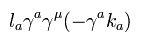
ここで次の公式を使う。
(Eq.15)
Eq.15 は 次の関係式を使うと証明できる。
(Eq.16)
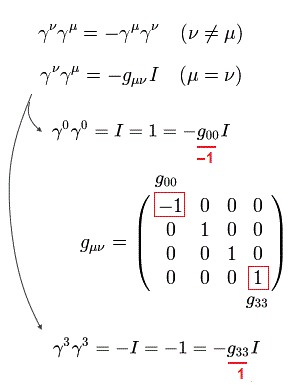
Eq.16 は 次のような意味である。
(Eq.H-1)
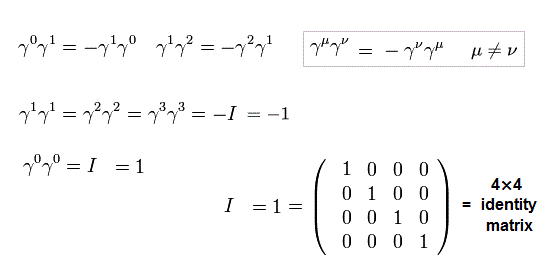
例えば、γ0γ0 = I ( = 4× 4, 単位行列 ),
(Eq.H-2)
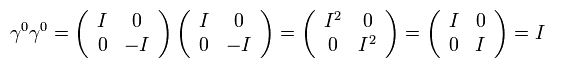
また、 γ行列は 次のような反交換関係を満たす。
(Eq.H-3)
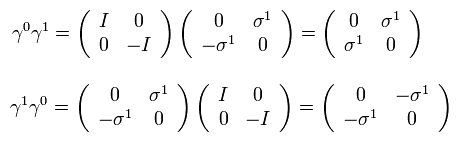
次に Eq.15 を証明する。 例えば Eq.15 の μ がゼロのとき、
(Eq.H-4)
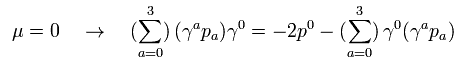
Eq.16 と Eq.H-1 の関係を用いると、Eq.H-4 の左辺は、
(Eq.H-5)
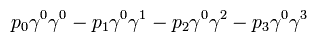
ここでは 反交換関係を用いた。
Eq.H-5 は次に等しい。
(Eq.H-6)
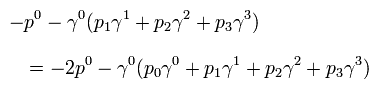
ここでは
(Eq.H-7)
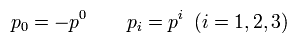
結果的に Eq.H-4 が正しいことが分かった。
( 同様に Eq.15 の他の数字のときも正しいことも分かる。 )
また、次の公式も使う。
(Eq.17)

μ が ν と異なるときは、 それは 奇関数となるため、積分すると Eq.17 はゼロになる。
gμν を Eq.17 の両辺に付加すると、
(Eq.17-2)
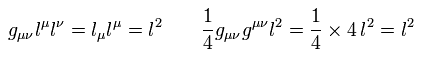
ここでは次を使った。
(Eq.17-3)
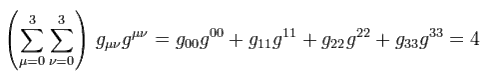
よって Eq.17 が正しいことが分かる。
Eq.15 を使うと、Eq.14 は、
(Eq.18)
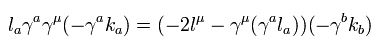
ここで 右側の γ と k の 添え字 a を b に変更している。
つまり、l と k をそれぞれ1つずつ含む項は ( k → l ) のように変更することができる。
(Eq.20)
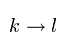
なぜなら、 l と k の差の部分は もう1つの l の奇関数の性質によって積分で消えてしまうからである。
すると、Eq.18 の最初の項は、(Eq.17 を用いて)
(Eq.21)
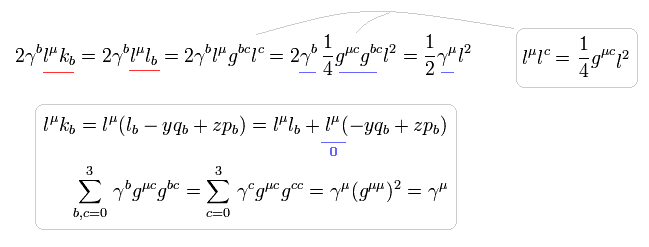
ここでは c と b に関して 0-3 成分の和をとった。
計量テンソルgより、μ = b = c のケースのみ残る。 そのため gμcgbc = 1.
また、Eq.18 の2番目の項は 次のようになる。
(Eq.22)
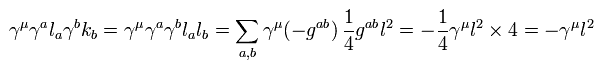
ここでは γaγb = -gab.
また Eq.17 と Eq.17-3 を用いた。
Eq.3 (2行目) の最初の項, Eq.21, Eq.22 を足し合わせると、
(Eq.22-2)
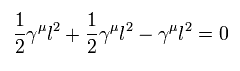
結果、Eq.3 を証明することができた。
(Fig.1) Eq.3 = Eq.10 のまとめ。

次に Eq.85 (= Eq.3 ) が このページ の Eq.88 (= Eq.23 ) に等しいことを証明する。
(Eq.23) = (Eq.88)

ここでは ディラック方程式が満たす 次の関係式を用いる必要がある ( このページ (Eq.5-12) も参照のこと。)
(Eq.5-12)

つまり、
(Eq.24)
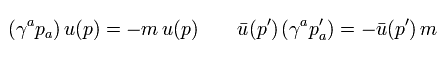
運動量とエネルギーは 次のように保存されている。
(Eq.25)
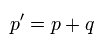
Eq.25 では、p と p' は それぞれ "in" と "out" の電子を表している。
重要な点は Eq.5-12 と Eq.25 を満たす必要があるとき、"q" は 仮想光子になり、 これは 相対論に従わない。
Eq.24 と E.25 から、
(Eq.26)
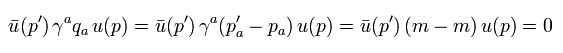
Eq.24 と Eq.25 を使うと、Eq.23 (1) の 2項目は、
(Eq.27)
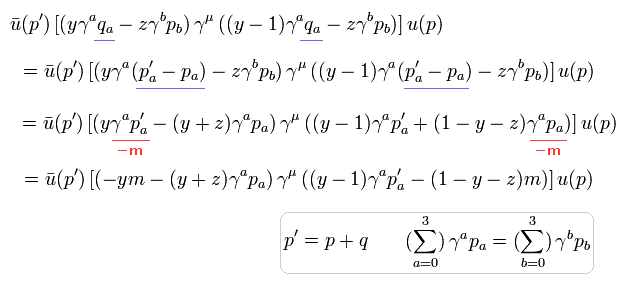
(Eq.15)

Eq.15 と Eq.24 を使うと、Eq.27 の最後の行に含まれる 項は,次のように変化する。
(Eq.28)

また Eq.27 の最後の行に含まれる 別の項は
(Eq.29)
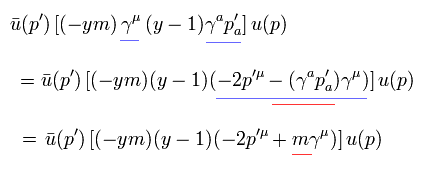
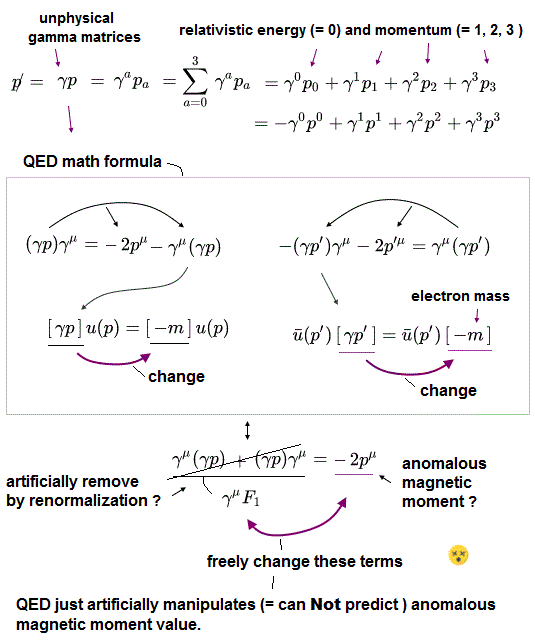
お気づきのとおり、彼らは p を γμ の右、p' を 左に移動させ "-m" に変更させようとしている。
そのため もし 仮想光子 "q" がゼロのとき、p' = p となり、わざわざ "-m" に変更するために それらを移動する必要がなくなる。
また Eq.27 の最後の行に含まれる 別の項は
(Eq.30)
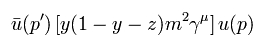
そして Eq.27 の最後の項は
(Eq.31)
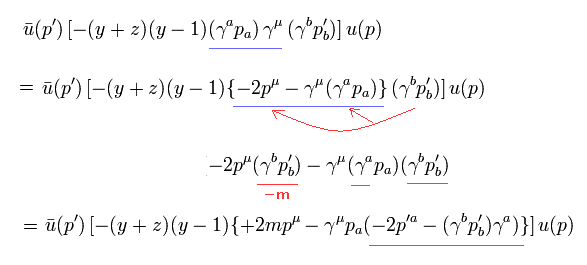
Eq.15 と Eq.24 を使って、Eq.31 に含まれる1つの項は
(Eq.32)
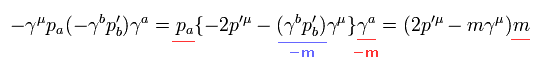
Eq.25 を使って、Eq.31 の別の項は、
(Eq.33)

ここでは 次の関係式を使っている。
(Eq.34)
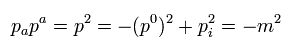
別の質量殻条件は、
(Eq.35)
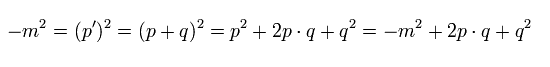
Eq.35 より、
(Eq.36)
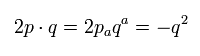
後で q2 = 0 にするため pq = 0 になる。この場合 仮想光子 q 自体が ゼロになる ( q = 0 ) 、
すると、g因子の値は 1つに決まらないことになる。
上記の計算結果をすべて足せば Eq.23 を証明できる。
( p' = p + q、 x + y + z = 1、 また Eq.23 の残りの項も足し合わせる。)
(Fig.2) Eq.23 のまとめ。
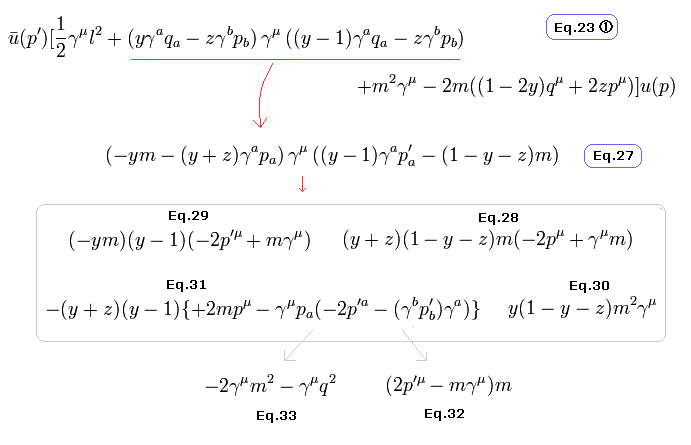
次に実際に足し合わせてみる。
最初に γμ 項 (= 頂点 ) の外の値を計算する。
Eq.23-1 の 2行目から γ を含んでいない 項をピックアップする。
(Eq.37)
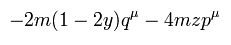
Eq.28 と Eq.31 から、 pμ の項は、
(Eq.38)

Eq.37 と Eq.38 の項から、pμ 項の合計 は、
(Eq.39)
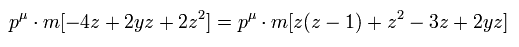
Eq.29 と Eq.32 (= Eq.31 の1つ ) から、p'μ 項の合計 は、
(Eq.40)
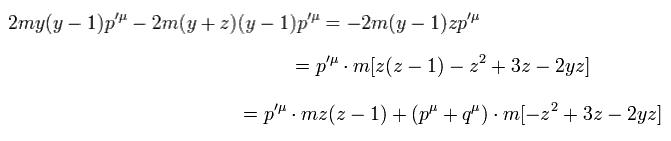
ここでは p' = p + q を使用している。
Eq.37 と Eq.40 から、qμ 項の合計 は、
(Eq.41)
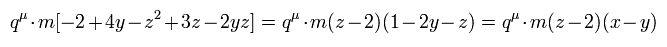
ここでは x + y + z = 1 を使っている。
Eq.39、 Eq.40、 Eq.41 から、 Eq.23-2 の2行目を得ることができる。
次に、Eq.28、 Eq.29、 Eq.30、 Eq.32 (= Eq.31 の1つ )、 Eq.33 (= Eq.31 の1つ )、 Eq.23-1 の2行目より、 γ 内の m2 項の合計 は、
(Eq.42)
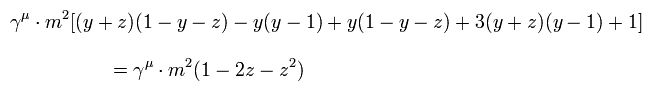
Eq.33 (= Eq.31 の1つ ) から、γ 内の q2 の項
(Eq.43)
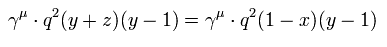
結果、Eq.23-2 の最初の行を得ることができた。
このセクションは このページの Eq.4-7 (Eq.4-4) から Eq.4-11 の内容を移したものである。
(Eq.4-4)
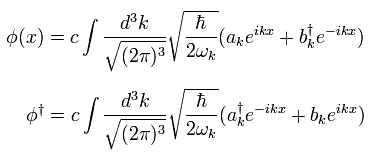
例えば、次の 伝播関数を計算する。 これは 粒子の伝播を意味するものである。
(Eq.4-7)
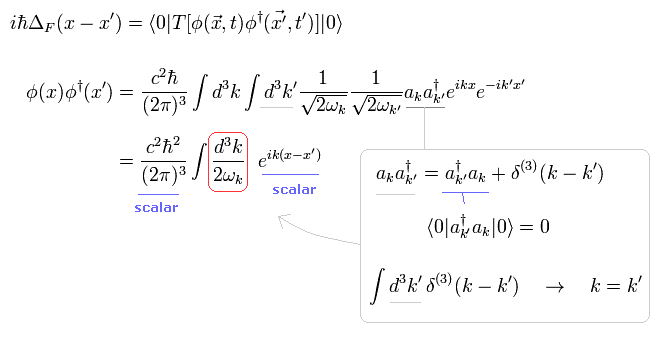
ここでは Eq.4-19 を用いている。
(Eq.4-19)
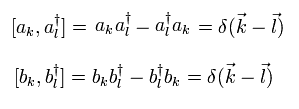
Eq.4-4 の2つの ω の平方根は 次のように変化する。
(Eq.4-8)
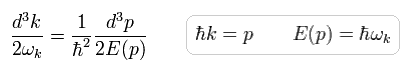
1つの d3k は積分するため、もう1つの k のみ残っている。
ここで 次の デルタ関数の公式を使う。
(Eq.4-9)
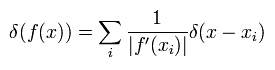
Eq.4-9 の公式を利用すると、 次の式を得る。
(Eq.4-10)
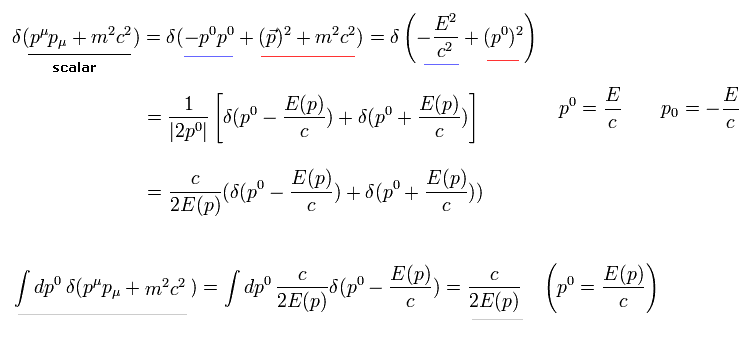
ここでは Eq.4-1 を使った。
(Eq.4-1)
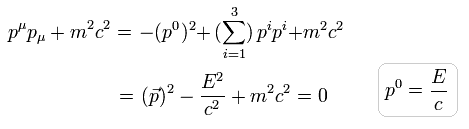
Eq.4-10 に d4p を付け加えて Eq.4-10 を p0 で積分すると 次の式を得る。
(Eq.4-11)
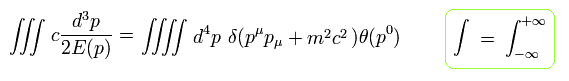
ここで θ は "階段関数" を意味する。
Eq.4-11 は d4p 積分と Eq.4-1 を含むため、これは ローレンツ不変である。
もちろん、ローレンツ不変にするには この積分範囲を マイナス無限大から無限大までする必要がある。
つまり Eq.4-8 も ローレンツ不変である。
お気づきのとおり、 c や h などの係数は ローレンツ変換を不変に保ったままでも 自由に, 変更可能である。
そのため、我々が "人為的に" 正しいエネルギーを得るために これらの値をいじることは可能なのである。

2011/6/1 updated This site is link free.