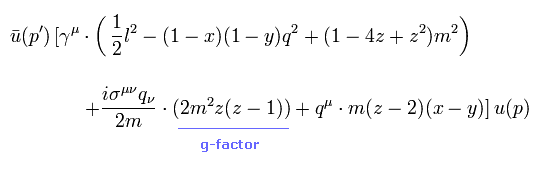
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは実在しない。
特殊相対論は間違っている。
QED の異常磁気モーメントの計算の詳細。
量子力学が非常に奇妙な世界にも関わらず信頼されている最も主要な要因の1つが 量子電磁力学における異常磁気モーメントの高次の計算の正確さであろう。
ラムシフトは これに比べて非常に難しい実験で曖昧な部分が多い。
また、QED のラムシフトの計算も 異常磁気能率に比して 別の自己エネルギーを組み合わせたりだとか 少し実験結果に合わせるために 技巧に走る傾向にある。
このページでは、この異常磁気モーメントの QED による計算値が 実は
かなり込み入った計算だが、実は 通常の自由粒子のディラック方程式 (= 質量殻 ) と γ行列の関係式を用いれば g因子の計算ができ、かつ操作も可能であることを示す。
このページでは 電子を扱っているが、質量定数などの部分を変更すれば そのまま他の粒子に適用可能である。
(Eq.1) 標準的なg因子。
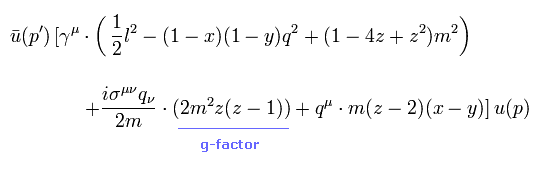
(Eq.2) 操作されたg因子。
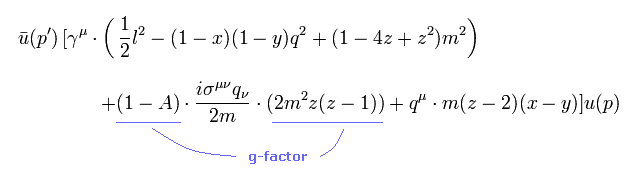
Eq.2 の青の部分が g因子の操作された部分である ( "A" の値は 任意である。 ).
結果的に g因子は 人為的に 操作できるのである。
このページ (Eq.5-12)に示すように、 自由粒子のディラック方程式 (= 質量殻 ) は
(Eq.3)
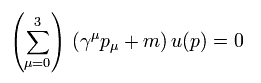
同じ添え字 (= μ) が 同一の項で 2回使用されているとき、 4つのベクトル (0-3) の合計を意味する。
ここでは 自然単位 ħ = 1、 c=1、 ( -1, 1, 1, 1, ) バージョンの計量テンソルを使用している。
そのため ディラック方程式は 次のように表せる。
(Eq.4)
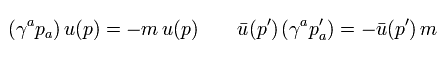
ここでは 添え字 "a" に関して 0 から 3 を足し合わせている。
このページに示したように、ディラックのγ行列は 次の関係式を満た
(Eq.5)
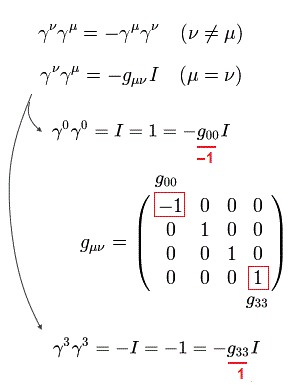
Eq.5 は、
(Eq.6)
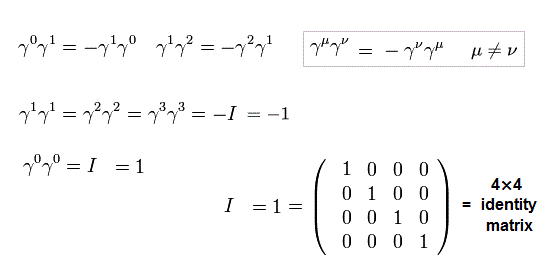
例えば、 γ0γ0 = I ( = 4× 4、単位行列 )、
(Eq.7)
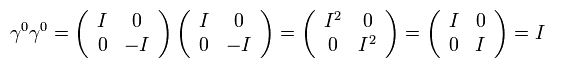
また γ 行列は 次のように 反交換関係を満たす。
(Eq.8)
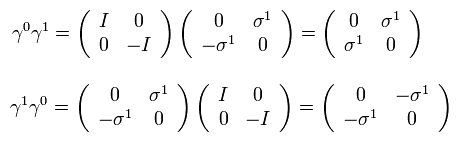
Eq.5 の関係式を用いると、Eq.3 のディラック方程式は クライン・ゴルドン方程式に等しいことがわかる。
(Eq.9)
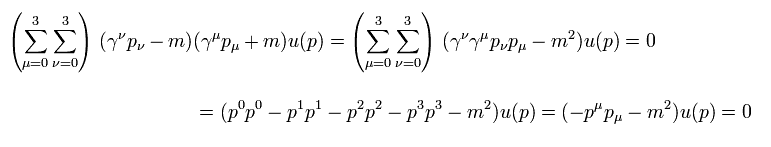
ここでは ( -1, 1, 1, 1 ) バージョンの計量テンソルを使用している。
γ行列の 反交換の性質のため、他の項は消える。
このページに示したように、2つの電子 ( in と out ) と 1つの光子の 次の関係式が ここでは使用されている。
(Eq.10)
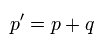
Eq.10 と Eq.4 を満たすということは、この光子は アインシュタインの質量殻条件に従わない仮想光子であることを意味する。
つまり この光子 q は タキオンである。
Eq.9 のように、Eq.4 のディラック方程式は 次のクライン・ゴルドン方程式に等しい。
(Eq.11)
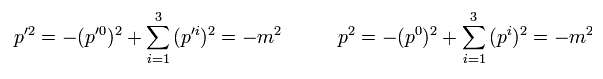
各電子 ( p' と p ) は アインシュタインのエネルギーと運動量の関係式を満足する。
Eq.10 と Eq.11 から、 次を得る。
(Eq.12)
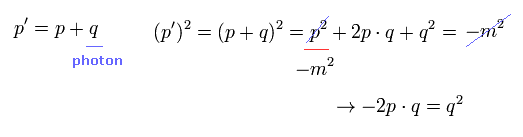
QED の g因子の計算では、g因子の値を得るために q2 = 0 (= 光子の質量ゼロ ) の条件を 選ぶ必要がある。
つまり "pq" もゼロになる。
(Eq.13)
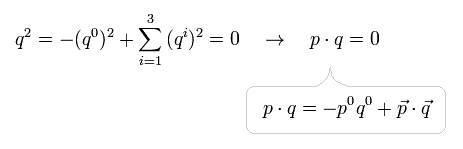
ここで "pq" も アインシュタインの公式を意味している。
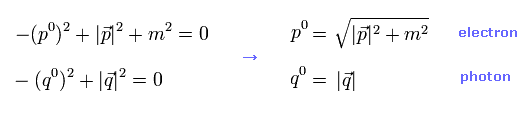
つまり、 "pq" を 次のように表せる。
(Eq.15)
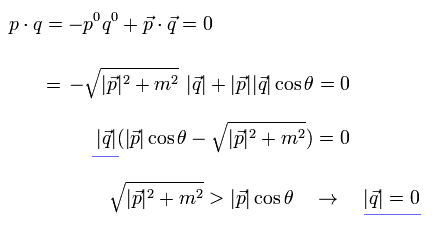
Eq.15 から、"q" のすべての成分は ゼロになるため、 p' = p となる。
(Eq.16)
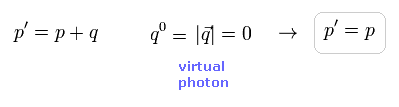
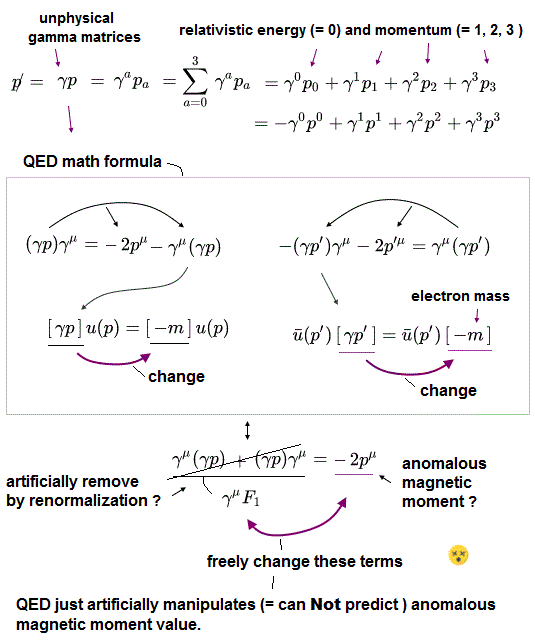
これらの 非常に緩い条件 (= 仮想光子が質量殻を満たす ) の下で、 QED は 他のものも含めて 様々な値を操作できることになる。
このセクションでは この事実を明確に説明することにする。
つまり 自然界の法則は 様々な値を決定するのに QED に従っていないのである。
なぜなら 自然界の法則が QED に従っているとしたら、g因子は 単一の値に決まらなければならないからである。
( また QED は 単純に 基本的な数学の計算が間違っている。)
通常のディラック方程式に加えて、次の重要な関係式を用いる。
(Eq.17)
Eq.17 は g因子の余分な値を γ の頂点の部分に移動させ 人為的に除去するのに非常に重要である。
例えば Eq.17 の μ がゼロのとき、
(Eq.18)
Eq.5 と Eq.6 の関係式を用いると、Eq.18 の左側は
(Eq.19)
ここでは 反交換関係を使用している。
Eq.19 は 次に等しい。
(Eq.20)
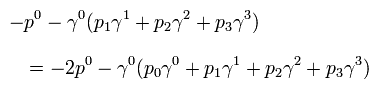
ここでは
(Eq.21)
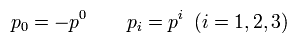
結果的に Eq.18 を証明することができた。
( 同様に Eq.17 も正しいことが分かる。 )
このページに示したように、次を得た。
(Eq.88)
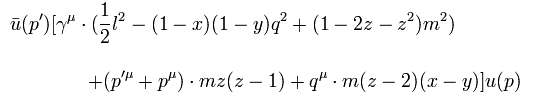
次の関係式を Eq.88 に使用すると、Eq.1 を得ることができる。
(Eq.22)
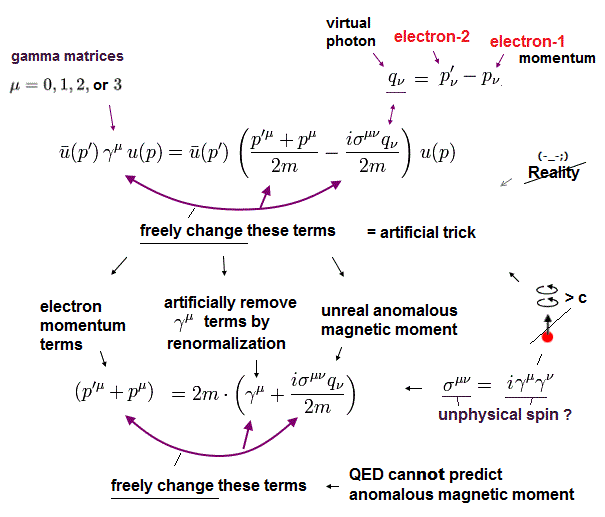
最も重要なところは 次の項の変化である。
(Eq.23)
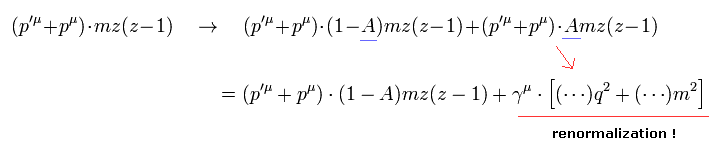
ここでは "A" の値は 任意である。
Eq.23 の操作ができると、g因子は自由に操作できることになる。
( q2=0 と γ の項の繰り込みも用いて。 )
Eq.17 の重要な関係式を用いて、
(Eq.24)
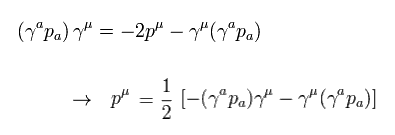
次を得る。
(Eq.25)
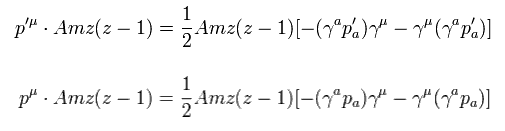
Eq.4 の 通常のディラック方程式を用いると
(Eq.4)
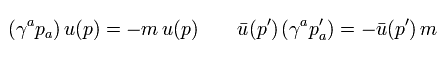
Eq.25 の上部の式の最初の項は
(Eq.26)
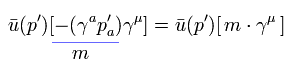
(Eq.27) 右サイドの p' の 左サイドへの移動。
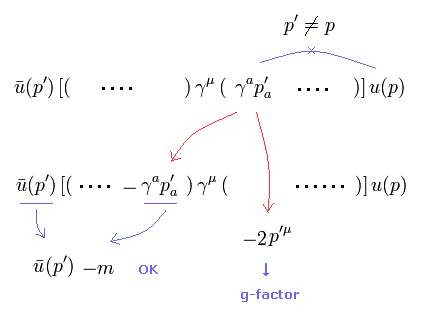
Eq.27 では、 p' が右サイドにあるとき、Eq.4 を用いて それを -m に変更できない。
そのため p' を左サイドへ移動させて それを -m に変化させている。
この過程においても g因子の一部が生成される。
しかし Eq.16 に示すように、仮想光子が q = 0 のとき、それを移動させることなく 自由に "-m" に変更できる。
(Eq.28)
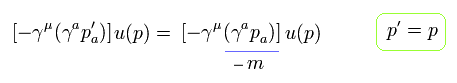
結果的に Eq.25 上部のすべての項を " γμ m " の項に変更することができる。
つまり g因子の操作に成功したというわけである。
(Eq.29) 仮想光子 q = 0 → g因子は自由に操作できる。

同様に、Eq.25 の下の項も " γμ m " の項に変更できる。
結果的に 元の式を次のように変更できることになる。
(Eq.30)
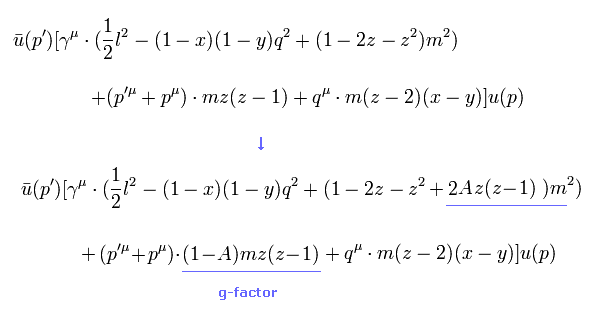
Eq.22 の置き換えを Eq.30 に使用すると、Eq.2 の 操作されたg因子が得られることになる。
(Eq.2) 操作されたg因子 !
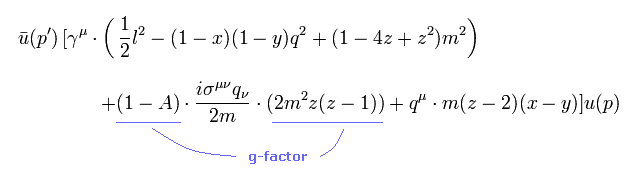
重要なカギとなるプレイヤーは このページに示したように 仮想光子である。
( もちろん、仮想光子が g因子のところに現れた時点で QED は間違いということになる。なぜなら それは相対論に従わないからである。)
(Fig.1) p' = p + q. ( q = 0 )
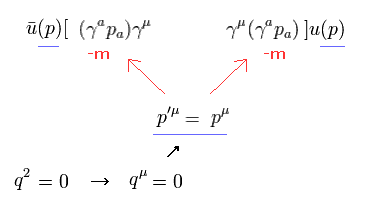
Fig.1 に示すように、 q = 0 のとき、 p' と p の違いはなくなる。
左 (p') と 右 (p) サイドが "p" になるため、 g因子は 簡単に変更できる。
また Eq.1 の 頂点 (スピン) 補正は ラムシフトの1部をしても使用されている。
つまり ラムシフトの値も 単一のものに 定まらない ことになる。
( ただし QED によるラムシフトの計算は もっと人為的で込み入っているが・・。)
このページに示したように、
(Eq.99)

(Eq.100)
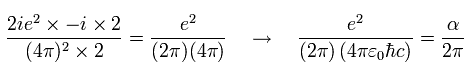
(Eq.103)
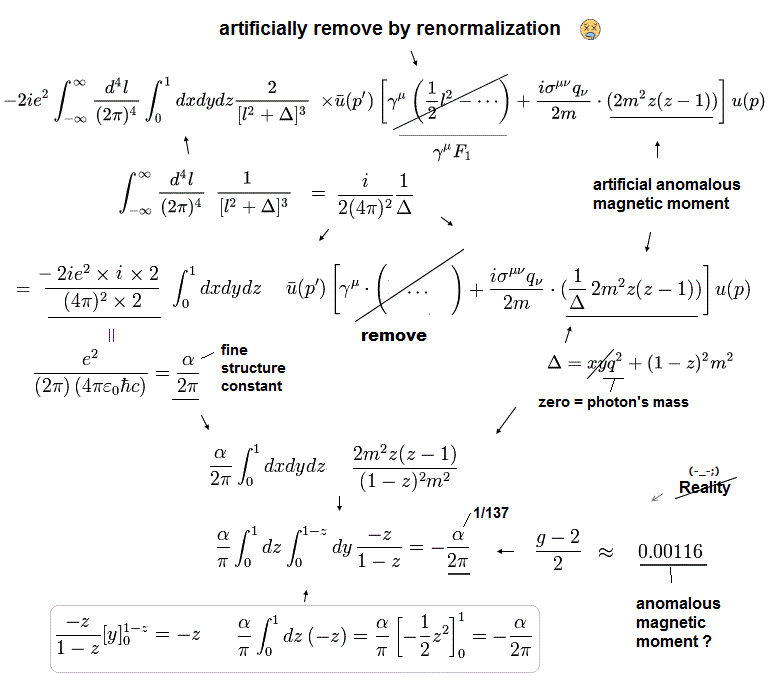
(Eq.107)
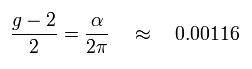
つまり Eq.2 において、Eq.107 のこの値は 0.00116 × (1-A) になるのである。
この A は 任意の値を取れる。
もちろん、すべてのオーダーで、"ボーア磁子" が使用されているため、この操作は可能である。

2013/1/25 updated This site is link free.