トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。単なる数学上の産物。
微細構造定数 (fine structure) の真実。
繰り込みによる 電子g因子計算の真実。
ディラック方程式を用いると、電子のg因子が "自然に" 得られると言われている。
( さらに 量子電磁力学の 繰り込みによって 少し補正ができるとされているが、この補正は ディラックのg因子 2 をベースにしている。)
(Fig.1) 電子スピン (= ボーア磁子 ) = 円運動 (= ボーア磁子 ) ?
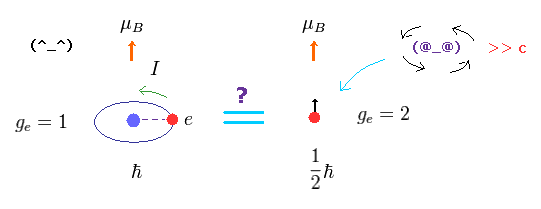
しかし このページに示したように、もし ボーア模型を使用すると、そのg因子は 1 になり、その最小の角運動量は ħ ( 1/2 ħ でなく ) になる。
結果的に 実験で直接測定できる 磁気モーメント (= g因子 × 角運動量 ) は ボーア軌道と 電子スピンで同じになる。
( 1 × 1ħ = 2 × 1/2ħ 。)
さらに ボーア軌道を使用すれば、超光速の電子のスピン速度や 奇妙な2価性に振り回されることがなくなる。
ところで この電子のg因子 2 というのは 本当に ディラック方程式からの 自然な結果なのだろうか?
また どうして 2 じゃなくて 例えば 1.7、3.5、2.3 ではだめなのだろうか?
ここでは 実際に ディラック方程式からg因子を導出する。
重要な点は 電子の磁気モーメント (磁気能率) は 純粋に ボーア軌道に由来しているということである。(= ボーア磁子。 )
もし このページ ( 場の量子論 ) を まだ読んでいなければ 先に読んで欲しい。
このページでは ミンコフスキーの計量テンソル g は
(Eq.1)
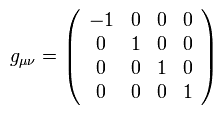
γ 行列は、
(Eq.2)
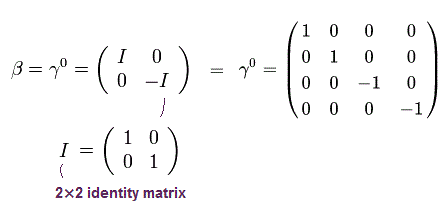
" I " は 2 × 2 単位行列である。
また
(Eq.3)
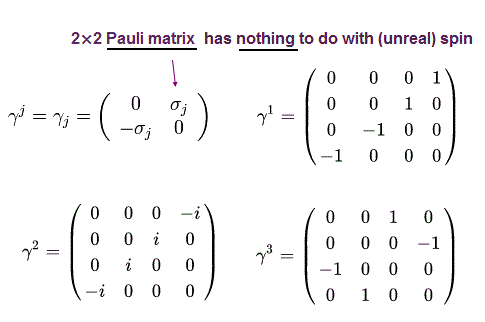
ここで σj は 2 × 2 パウリ行列である。
(Eq.4)
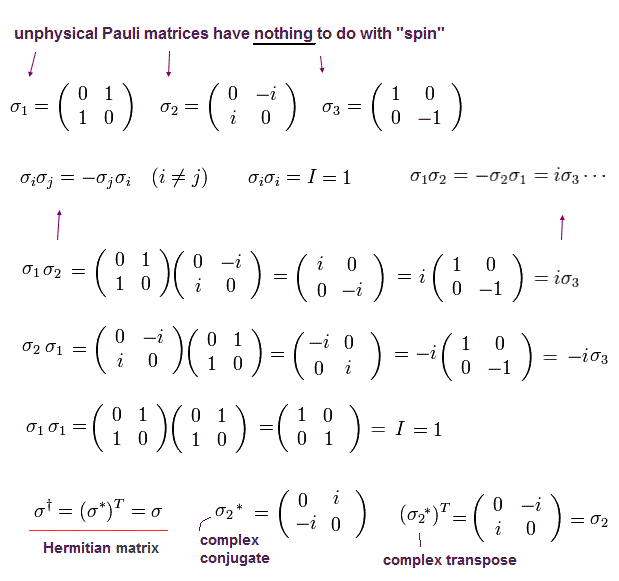
このページ (Eq.5-12) に示したように、ディラック方程式は、
(Eq.5)

上記の γ 行列を用いると 次を得る。
(Eq.6)
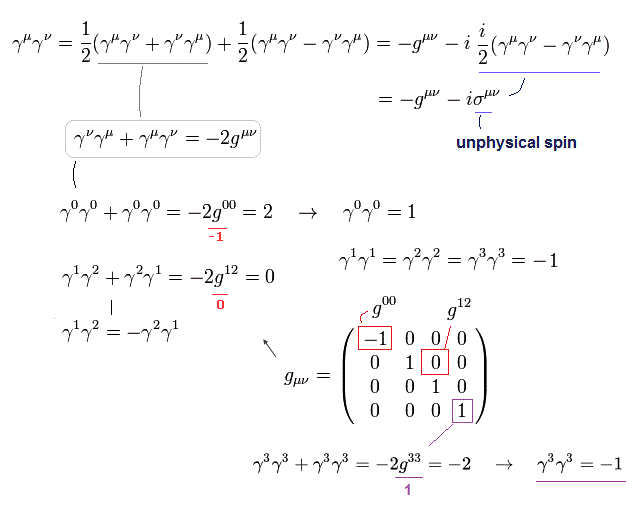
Eq.6 の σ は 次のように定義される ( この σ は 4 × 4 行列である。 )
(Eq.7)

これが 4 × 4 のスピン形式である。
お気づきのとおり、この スピン行列には ゼロ成分が含まれており、磁気モーメントとは 関係がない。
これは スカラーポテンシャルとベクトルポテンシャルを同じ次数にしたからである。
しかし 彼らは この形式から 磁気モーメントを得ようとしている。
ここで 次を用いる。
(Eq.8)
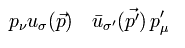
Eq.6 の右側から Eq.8 の最初の演算子をかけると、
(Eq.9)

ここでは Eq.5 を使用した。
Eq.6 の左側から Eq.8 の2番目の演算子をかけると、
(Eq.10)

最後の項は σ の 反対称の性質を使っている ( Eq.7 も参照のこと )。
Eq.9 の 両辺を -mc で割ると、
(Eq.11)
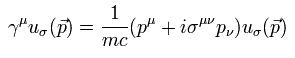
Eq.10 の μ と ν を入れ替えて、それを -mc で割ると、
(Eq.12)
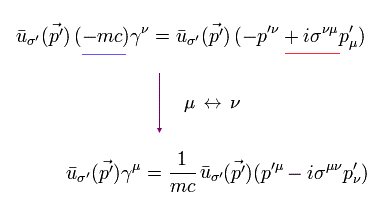
Eq.11 の左側から Eq.13 の最初の演算子をかけて、 Eq.12 の右側から Eq.13 の2番目の演算子をかける。
(Eq. 13)
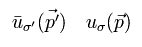
そして これら2つの結果を足し合わせて それを 2 で割ると 次を得る。
(Eq.14)
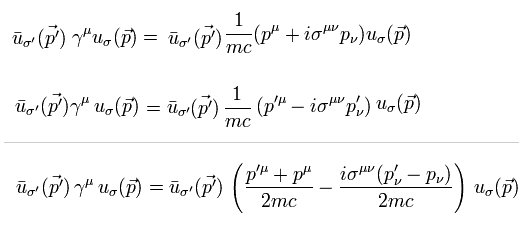
ここでは
(Eq.15)
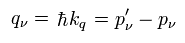
この "q" は ( 仮想 ) 光子 = 外磁場 である。
この定義によると、電子の運動量 (= 速度 ) が 定常 ( p' - p = 0 ) のとき、外磁場は存在していても、ゼロになってしまう。
これは奇妙である。
p' - p = q の関係式と c = ħ = 1 の定義を用いると、 Eq.14 は、
(Eq.16)
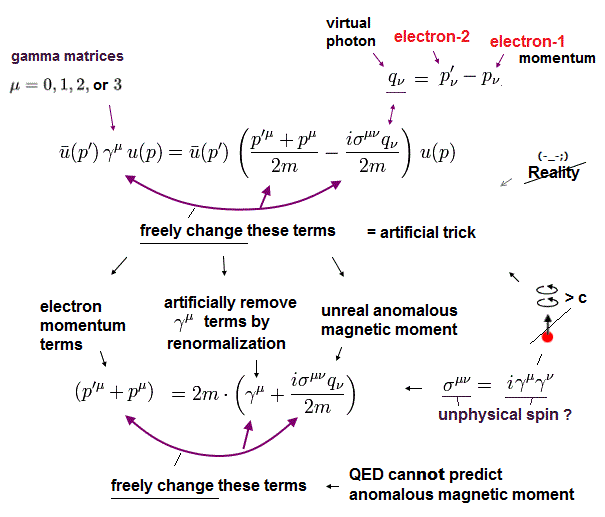
Eq.16 は g因子の繰り込み計算 に使用される重要な式である。
このページに示したように、ベクトルポテンシャル A は 指数関数を含んでおり、Eq.7 と Eq.16 から スピン・磁気相互作用 が得られる。
(Eq.17)
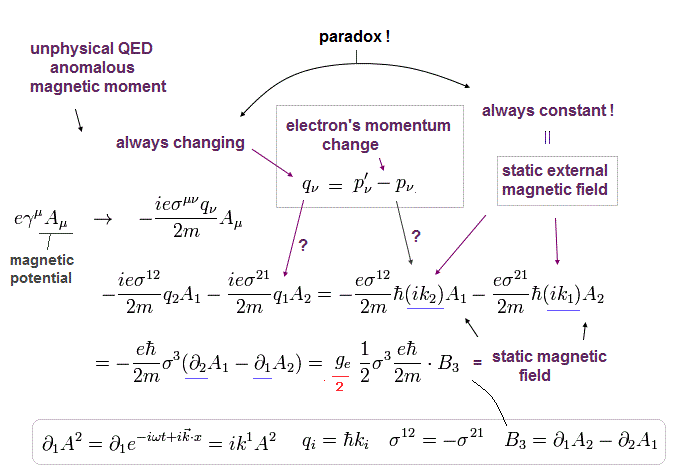
ご存じのとおり、スピン角運動量を "1/2" と定義する。すると 電子のg因子 (= ge ) は "2" となる。
つまり g因子 "2" というのは 自然な帰結ではないのである。
"ボーア磁子" に合わせるために "2" になったのである。
ボーア磁子は、
(Eq.18)

スピンの "z" 成分は、
(Eq.19)
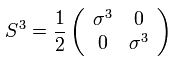
シュレディンガー方程式の形式においても、量子力学は 次のような数学的なトリックを使用している。
( このページも参照のこと。 )
(Eq.20)
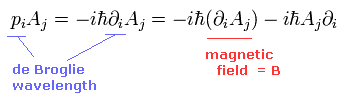
ここで p (= 電子の運動量 ) は 導関数を含んでおり、それは Aj の前と後に作用している。
つまり 電子のドブロイ波 が 外磁場のベクトルポテンシャルの微分に すり変わっているのである。
これも奇妙である。
ご存じのとおり、時間に依存する シュレディンガー方程式は 次のように表せる。
(Eq.21)
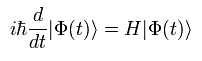
すなわち シュレディンガー描像における 固有関数 ( Φ(t) ) は 時間変数 (= t ) を含んでいる。
初期状態 ( t = 0 ) を次のように定義する。
(Eq.22)
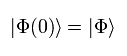
ハミルトニアン (H) が 時間非依存のとき、 Eq.21 の解は、
(Eq.23)
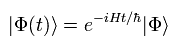
場の量子論 (QFT) は シュレディンガー描像の代わりに ハイゼンベルグ描像をよく使用する。
なぜなら、繰りこみの 主要な場は 固有関数よりもむしろ 演算子だからである。
(固有関数そのものは QFT や QED では あまり重要でない。)
つまり ハイゼンベルグ描像では 次のように 演算子 A(t) が 時間依存性なのである。
(Eq.24)
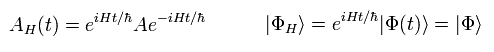
( 代わりに 固有関数 (Φ) は ハイゼンベルグ描像では 時間非依存である。)
Eq.24 から その A(t) が 次の ハイゼンベルグの運動方程式 を満たすことが分かる。
(Eq.25)
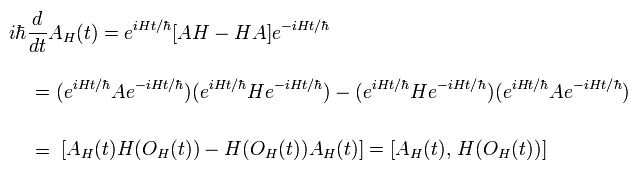
ここでは ハミルトニアンの各演算子 ( OH(t) ) は Eq.24 のように表現される。
ハミルトニアンは 次のように分割できる。
(Eq.26)
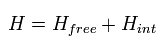
それぞれ、自由エネルギー項 と 相互作用項を表している。
ここで 相互作用描像の演算子を次のように定義する。
(Eq.27)
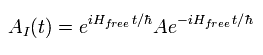
QED において 重要な部分は まさに相互作用項にあり、固有関数が 相互作用ハミルトニアンによって次のように時間発展すると仮定する。
(Eq.28)

ここで U(t) は、
(Eq.29)
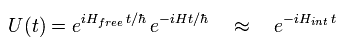
U(t) は 相互作用描像の伝播関数 もしくは 時間発展演算子と呼ばれるものである。
Eq.29 の共役な演算子は、
(Eq.30)
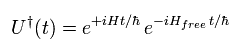
つまり、 U† U = 1 となり、 U(t) は ユニタリー演算子である。
Eq.27 の 相互作用描像の演算子 AI(t) は Eq.4 の ハイゼンベルグ描像の演算子 AH(t) と Eq.29 と Eq.30 の U(t) を用いて、次のように表せる。
(Eq.31)
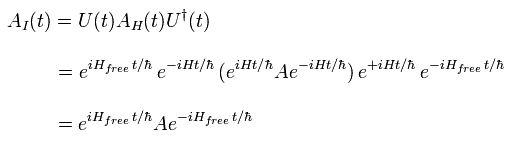
電子のg因子の摂動計算をするためには Eq.29 よりも もっと具体的な表現の U(t) が必要である。
Eq.29 より、U(t) の簡単な微分方程式は、
(Eq.32)
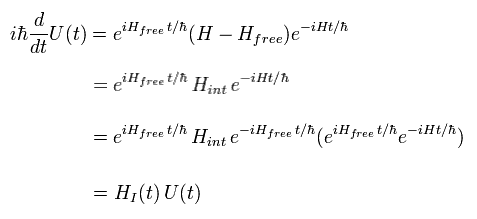
ここで 初期状態は、 U(0) = 1.
これはつまり、 Eq.32 は 次に等しくなることを意味する。
(Eq.33)
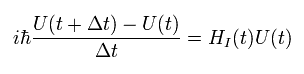
よって、
(Eq.34)
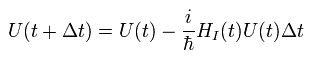
Eq.34 の右側から Eq.30 の U† をかけると、
(Eq.35)
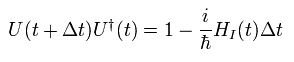
ここで 次のように定義する。
(Eq.36)
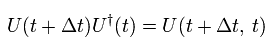
( なぜなら U† は 時間が ゼロから t への後退を意味するからである。 )
Eq.36 を使うと、Eq.35 は次のように表せる。
(Eq.37)
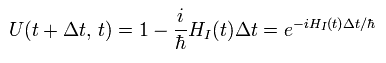
Eq.37 は 無限小時間である。 Eq.37 の U を 次のように結合すると、
(Eq.38)
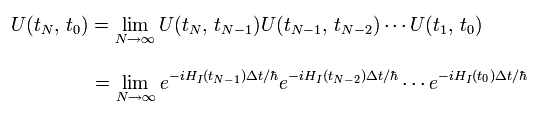
一般的に、相互作用ハミルトニアン ( HI(t) ) は 時間 t が異なると、交換しない。
Eq.38のいろんな U(t, t') は 時間が後になるほど左側というように 時間順序で並んでいることに注意。
そこで Eq.38を 次の 時間順序積演算子を使って 簡単に表現できる。
(Eq.39)
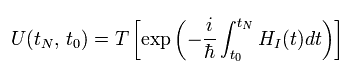
Eq.39は もし この記号 T を取り除くと、各 U(t, t') は Eq.38 のように 時間順序に 自動的に配列することを示している。
(つまり、この記号 T の中では 我々は自由に U(t, t') を交換することができるため、Eq.39 のような 1つの指数関数に結合できる。)
伝播関数は 場の演算子が 2つのみ含まれた ( 2 × φ ) 最も簡単な形式のグリーン関数である。
グリーン関数の一般化した形は、
(Eq.40)
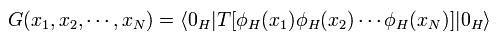
ここで H は 最初に説明した ハイゼンベルグ描像の意味である。
Eq.31 から ハイゼンベルグ描像と相互作用描像の演算子は、
(Eq.41)
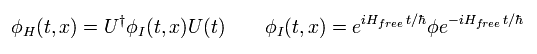
ここで ユニタリー演算子 U(t) は 次を満たす。
(Eq.42)
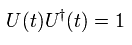
Eq.41 と Eq.42 を Eq.40 に代入して、
(Eq.43)
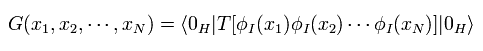
最初のセクションで言ったように 時間順序積 T の中では、演算子の順序を自由に変更できる。
時間 t = 0 のとき、真空のエネルギーがゼロと定義する。
(Eq.44)
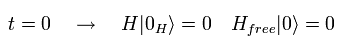
(注意: ハイゼンベルグ描像の真空は 普通の真空とは違う。 なぜなら それは 無限大の運動量を含む 無限の仮想粒子 を含んでいるからである。 )
Eq.44 から、
(Eq.45)
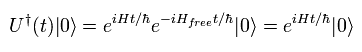
ハイゼンベルグ描像における 固有状態の完全系は、
(Eq.46)
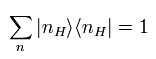
Eq.46 を Eq.45 に代入して、
(Eq.47)
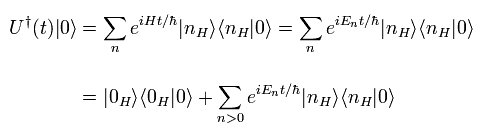
ここで En > 0 である。
ここで 次の虚数時間を考える。
(Eq.48)
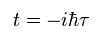
時間が → - ∞ のとき、
(Eq.49)
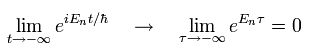
すなわち Eq.47 の ゼロエネルギーの状態のみ残ることになる。
( この部分は 非常にイメージが難しい。しかし 何度も言うように この”数学上の世界”が 場の量子論である。仕方がない。)
Eq.47 と Eq.49 から、
(Eq.50)
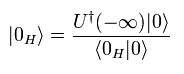
同じようにして ( Eq.45 から Eq.50 までと ), 次の式を得る。
(Eq.51)
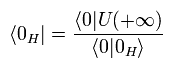
Eq.50 と Eq.51 から、
(Eq.52)
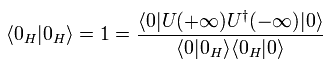
つまり、
(Eq.53)
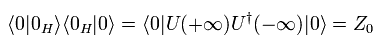
Eq.50, Eq.51, Eq.53 を使って、 Eq.43 の グリーン関数は、
(Eq.54)
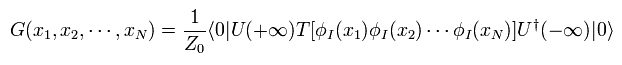
すでに述べたように、 U(t) 演算子を 時間順序積 T の中に入れると、 それらの順序を自由に変更できる。
(Eq.55)
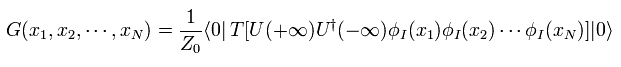
Eq.36 - Eq.39、 Eq.55 を使って、
(Eq.56)
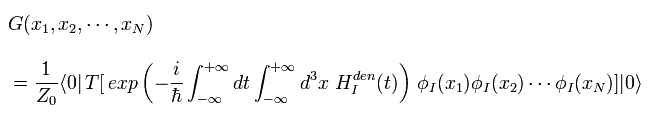
ここで Hden は 相互作用ハミルトニアン密度 である。 そのため Eq. 56 は それを空間座標で積分している。
Eq.53 の Z0 は U(t) に含まれる 無限大の 非結合のダイアグラム (真空泡) を表している。
そのため、分子の中の 遊離した 真空泡 は この分母の Z0 によって除去される。
結果として、それは 場の演算子 (φ) と結合したダイアグラムのすべての合計となる。
Eq.56 は ファインマンダイアグラムを表す基本となるので 非常に重要である。

2011/1/23 updated This site is link free.