(Eq.1)
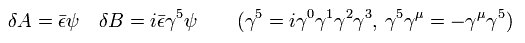
ここで 次を使っている。
(Eq.2)
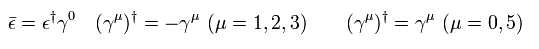
ε は ディラックスピノルの変化量 (× γ0) で、 ψ は 通常の ディラックスピノルを意味している。
つまり Eq.1 では、 変換後でも ボゾンの項は "数" (= 転置スピノル × スピノル ) のままである。
トップページ (2電子原子も含む正確な新ボーア模型)
超ひも理論は本当なの?
特殊相対論は間違い?
ひも理論から タキオンを除去するには 超対称性が必要である。
超対称性とは 超対称性変換のもとで 不変であることを意味している。
ここでは 通常の 4次元のラグランジアンを用いて ある形式のラグランジアンが 超対称性変換のもとで不変であることを示す。
( 超対称性粒子とは そのペアの粒子と 同じ質量などをもつが スピンが 1/2 異なるものをいう。)
超対称性変換のもとで、 ボゾン (= A と B ) は 次のように変化する。
(Eq.1)
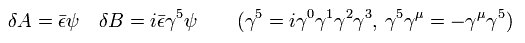
ここで 次を使っている。
(Eq.2)
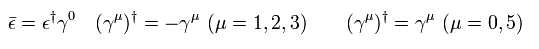
ε は ディラックスピノルの変化量 (× γ0) で、 ψ は 通常の ディラックスピノルを意味している。
つまり Eq.1 では、 変換後でも ボゾンの項は "数" (= 転置スピノル × スピノル ) のままである。
また フェルミ粒子 (= ψ ) は 次のように変化する。
(Eq.3)
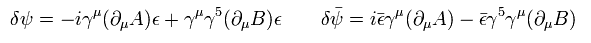
ここで A は "ボゾン" を意味している。
ここで 次のラグランジアンを考慮する。
(Eq.4)
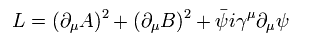
Eq.4 の最初の項は、 Eq.1 の超対称性変換で 次のように変化する。
(Eq.5)
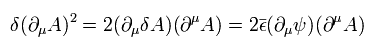
Eq.4 の2番目の項は 次のように変化する。 ( Eq.1 を使用して。)
(Eq.6)
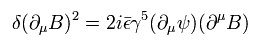
Eq.4 の3番目の項 (= フェルミ粒子 ) は次のように変化する。
(Eq.7)
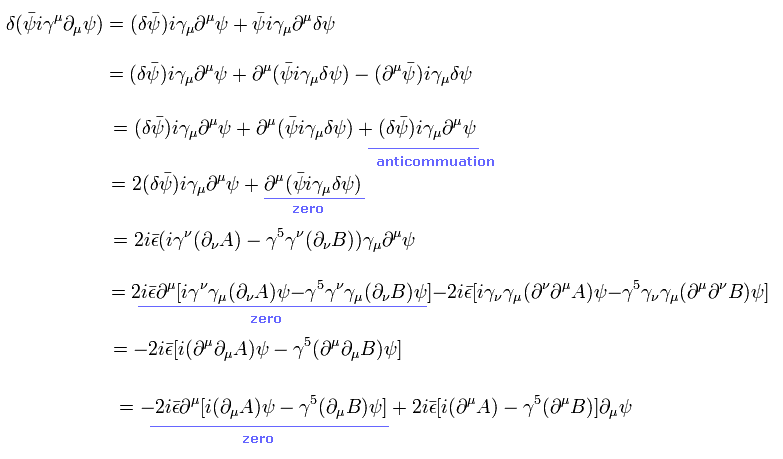
ここのみ (+1, -1, -1, -1) バージョンの計量テンソルを使用している。
また、ラグランジアンの作用積分によって、 全微分の項はゼロになっている。
Eq.5、 Eq.6、Eq.7 の合計はゼロである。
結果的に Eq.4 のラグランジアンは 超対称性変換のもとで 不変である。
しかし お気づきのとおり、Eq.1 と Eq.2 の変換形式や定義などは 非常に "人為的な"数学上のみのものであり、現実から遊離していると言わざるを得ない。
ひも理論は 通常の QED に比べて 紫外発散が少なくなる。
しかし ひも理論も 指数関数で表される 無限の調和振動子を使用している。
そのため、時間 t がゼロのとき、発散を生じさせる可能性をもっている。
(Eq.8)
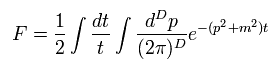
Eq.8 は D-次元から見た ウィック回転後の ある確率振幅を意味している。
t がゼロのとき、この指数関数は定数になり 打ち消されない。
Eq.8 のケースは ウィック回転後の t → 0 における 対数発散を意味している。
例えば、Eq.8 の 1/t は e-Et を エネルギーに関して積分すると得られる。
( この場合は、次元を合わせるため 1/t が使用されている。)
もしこの発散が残ると、重力を含む様々な複雑な相互作用が 発散してしまい、取り除くことが難しくなる。
Eq.8 の発散を防ぐため、ひも理論は F が t=0 を含まない定義を導入した。
しかし この定義を正確に使用するには この変換が 確率振幅の変化を生じさせないことを証明する必要があった。
Eq.8 の質量項 (=m ) は ひもの内部振動を意味している。
(Eq.9)
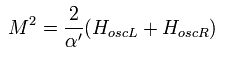
つまり Eq.8 は 次のように表せる。
(Eq.10)
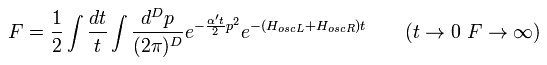
ここで 次の公式を使う。
(Eq.11)
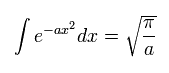
Eq.11 を使用すると、 Eq.10 は、
(Eq.12)
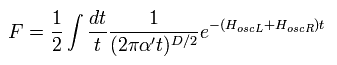
対称性を保つために、左回りと右回りのハミルトニアンが同じになる必要がある。
そのため 次の因子を付け加える必要がある。
(Eq.13)
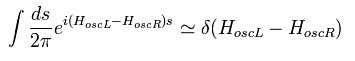
このページに示されるように、左回りと右回りの空間変数の符号は逆である。
そのため、Eq.13 の s を 2次元のひもの 空間変数のように扱える。
Eq.12 と Eq.13 を結合すると、
(Eq.14)
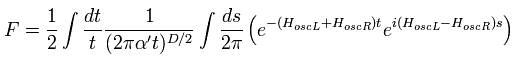
ここで 変数を次のように変換する。
(Eq.15)
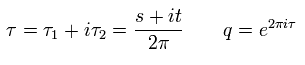
そのため
(Eq.16)
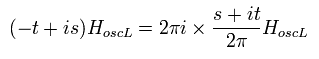
Eq.14 は次のように表せる。
(Eq.17)
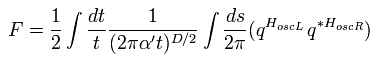
ここで 空間変数 s が -π から π の範囲、また 時間 t がゼロを避けると仮定する。
(Eq.18)
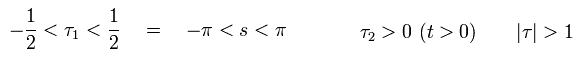
Eq.18 の定義は Eq.8 の発散を生じさせない。
Eq.18 の定義を有効にするには、Eq.18 の定義が 確率振幅全体に影響を与えないことを証明する必要がある。
ここで 次の変換 (= モジュラー変換 ) を使用する。
(Eq.19)
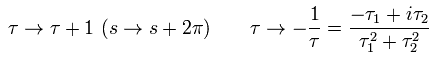
Eq.19 は 変数 "s" が 2π の間隔周期であることを意味している。
また 確率振幅が 2つの変数のスケール変換と "s" のフリップで変化しないことを意味している。
なぜなら、2-D の奇妙なひもを定義したとき、これらの2つの変数は 任意のものでなければならないからである。
このページの Eq.76 と Eq.84 で、ボゾンのハミルトニアンは、
(Eq.20)
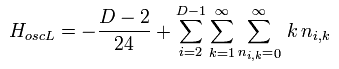
もちろん、ここでは 奇妙な ゼータ関数を使用している。
ボゾンの数は任意である ( "n" は 0 から ∞ )。
そのため その指数関数は、
(Eq.21)
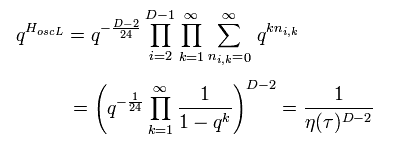
ここで qk の等比級数の和を計算している。
またここでは、 デデキンドのイータη関数を定義している。
(Eq.22)
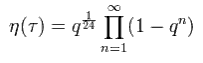
Eq.15、 Eq.21 から、 Eq.17 は次のように表せる。
(Eq.23)
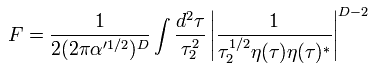
ここで次を使っている。
(Eq.24)
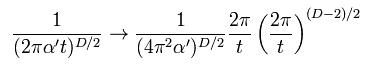
Eq.19 のモジュラー変換のもとで、
(Eq.25)
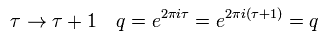
Eq.23 は 変化しない。
また デデキンドのイータ関数は次のように変化することが知られている。
(Eq.26)
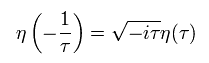
Eq.19 から、
(Eq.27)
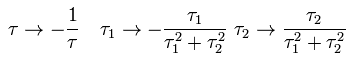
また Eq.15 から、
(Eq.28)
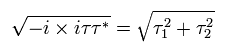
Eq.26、 Eq.27、Eq.28 から、Eq.23 の振幅は モジュラー変換 (Eq.19) で不変である。
(Eq.29)
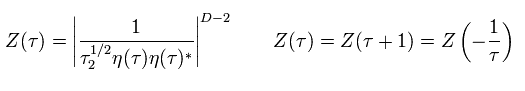
Eq.15 から、 Eq.23 の残りの部分も変化しない。
タキオンを除去するには、次のように "人為的な" 定義をしなければならない。
(Eq.30)
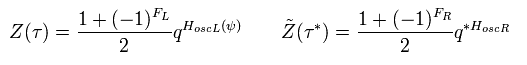
Eq.30 は GSO 射影 と呼ばれるものである。
(-1)FL は H が "奇数" の数の NS セクターのひもを含んでいるとき、それがマイナスになることを意味している。
つまり、Eq.30 のユニタリ変換のもとで、左回りと右回りの各ひもについて、偶数の数の NS セクターが含まれる状態のみ残すことになる。
NS セクターは 反周期境界条件、R セクターは 周期境界条件の意味である。
( 注意: R セクターの "R" と、右回りの "R" を混同しないように。)
そのため ボゾンとフェルミ粒子を含んだ振幅は ( D=10 のとき )、
(Eq.31)
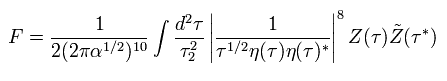
ボソンの部分は 上で示したように モジュラー変換で不変である。
そのため フェルミ粒子の部分の不変性を証明すればいい。
このページの Eq.99 から、 NS セクターのフェルミ粒子部分は、
(Eq.32)
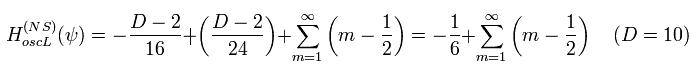
ここでは ボゾンの真空を除いている。
最初に、 Eq.30 の "1" の部分 (= (-1)FL なしのほう ) を考える。
GSO 射影なしの NS セクターは、
(Eq.33)
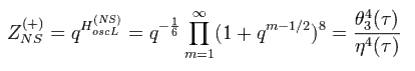
ボゾン (= 数 "n" が 0 から ∞) と違い、 フェルミ粒子の数 n は 反交換関係のため、"0" もしくは "1" しかとれない (= パウリの排他原理 )。
ここで 楕円シータθ関数 が次のように定義される。
(Eq.34)
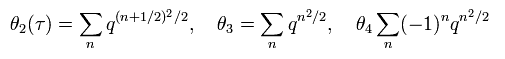
また、 "R" セクターのハミルトニアンは、
(Eq.35)
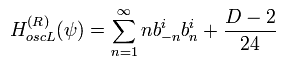
ここで
(Eq.36)
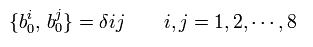
"R" セクターのフェルミ粒子は 反交換関係を満足するが、その角振動数はボゾンのように整数である。
( これは 単なる定義なため、このルールに従わなければならない。)
NS セクターと異なり、"R" セクターのフェルミ粒子は ゼロの角振動数 (= ゼロエネルギー) の "縮退" を含んでいる。
8 (= 10-2 ) の振動子は R-セクターのハミルトニアンと交換できる 4ペアの生成消滅演算子を含んでいる。
(Eq.37)
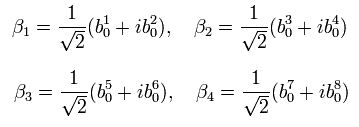
(Eq.38)
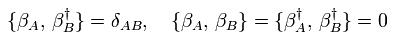
4種類の生成演算子は R-セクターの基底状態が 24 = 16 種類の状態 (=各ゼロエネルギー粒子があるかないか) を含んでいることを意味している。
結果的に Eq.35 から、 R-セクターの振幅 (D=10) は、
(Eq.39)
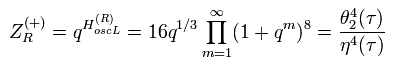
ここで n → m で フェルミ粒子の数は "0" か "1" である。
次に Eq.30 の (-1)FL が 振幅に作用する場合を考える。
NS-セクターのフェルミ粒子数が "1" のとき、 それはマイナスになる。そのため Eq.33 は、
(Eq.40)
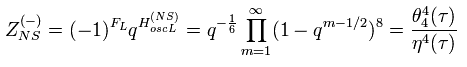
また、(-1)FL が作用すると、 "R"-セクター のフェルミ粒子はゼロになるとする。つまり (-1)FL は NS-セクターのみに作用することになる。
(Eq.41)
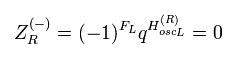
ここで (-1)FL のもとで、 NS-セクターの真空が "マイナス" になると仮定する。
(Eq.42)
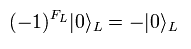
Eq.42 は NS-セクターの真空が Eq.30 の GSO 射影の結果 除去されることを意味している。
そのため GSO 射影のもとでのすべての結果をたすと、フェルミ粒子の分配関数は、
(Eq.43)
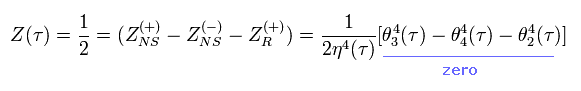
Eq.43 では、 位相の違いにより R-セクターの符号が逆になっている。
Eq.42 により、 GSO 射影のもとでの NS-セクターもマイナスになっている。
( これはちょっと思い浮かべるのが難しいが・・。 )
楕円シータ関数の公式によれば、Eq.43 の最後の項は 必ずゼロになる。
これは フェルミ粒子のケースも モジュラー不変であることを意味している。
この場合は D=10 の次元のときのみ成り立つ。
Eq.42 に示したように、NS-セクターの真空は Eq.30 の GSO 射影の結果 除去される。
また 同数の R セクターの 同じ質量をもつフェルミ粒子が ボゾンの真空をちょうど打ち消す (逆符号のため)。
また もちろん、NS と R セクターのひもは Eq.43 に示したように 同数である。
これはつまり 同じ質量をもつ超対称性粒子が タキオンの真空を排除したことを意味する。
( あなたがたは この非常に抽象的な理由を理解できただろうか?)
残念ながら、ここには 何の具体的なイメージやリアリティーがない。
現在のひも理論は ご覧のとおり、数学上のみの非現実的な世界の中だけをさまよっている感じである。
あなたがたはどう思われただろうか?
次元 "10" という値は、ゲージ固定と それによって生じるセントラルチャージのアノマリーの除去からも得られる。
最も重要な点は、これらの "数学的な"概念が この現実の世界と 実際にリンクしているかどうかということである。

2012/7/21 updated This site is link free.