ベクトル A を x で偏微分し、かつそれを一般座標変換すると、
(Eq.1)
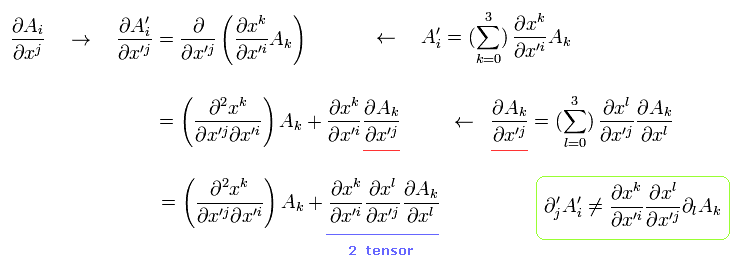
トップページ (2電子原子も含む正確な新ボーア模型)
一般相対性理論は本当に正しいのか??
もし このページ ( 一般、特殊相対論 ) の前半部分をまだ読んでいないようなら最初に読むように。
ベクトル A を x で偏微分し、かつそれを一般座標変換すると、
(Eq.1)
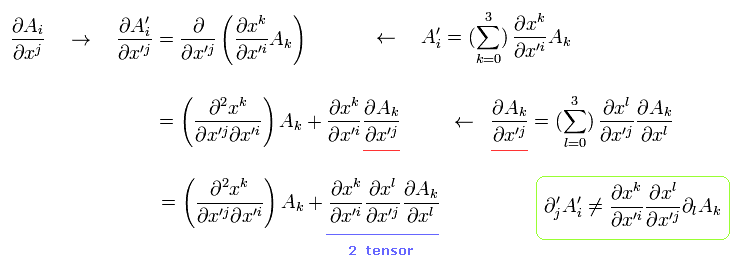
これは 次のミンコフスキー空間のときとは違う。
(Eq.2)
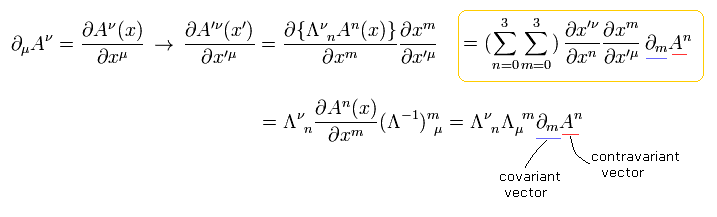
なぜなら 一般座標変換 (= "一般化された" ローレンツ変換 ) は 2回微分可能だからである ( Eq.1 の右辺の最初の項 )。
Eq.1 の 右辺の2項目のみだったら、ベクトルAの導関数は 座標変換に関してテンソルのように変化することを意味している。
もし 偏微分演算子が共変4元ベクトルでないとしたら、計算が非常にやっかいになってしまう。
そのため リーマン時空間では 新しい 微分 (= 共変微分 ) を次のように定義する。
(Eq.3)
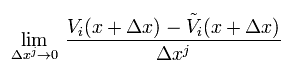
Eq.3 の 分子は x+Δx のみを含んでいるため Eq.1 の右辺第一項のような項がでてこなくなり テンソルとなる。このことは後で説明する。
いずれにしろ Eq.3 や Eq.4 の定義は 相対論の共変形式に合わせるための人為的な定義と言わざるを得ない。
ここでは チルド-V は 平行移動したベクトルであり、 次のように定義される。
(Eq.4)
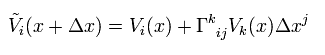
ここで 係数 Γ は クリストッフェル記号 (もしくは アフィン接続係数 ) と呼ぶものである。 また V(x) の変化量は もとの V(x) の値と、 Δx に比例すると仮定した。
また Eq.4 が次を満たすとする。
(Eq.5)
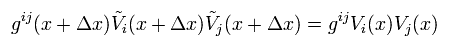
Eq.5 は 次に等しい。
(Eq.5-2)
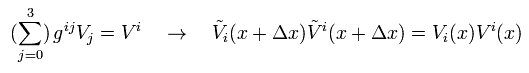
Eq.4 に示す 平行移動された チルド V の意味が理解できただろうか?
計量テンソル g(x) は 位置によって変化する。なぜなら 重力が位置によって異なるからである。
Eq.5 は 異なった場所 x でさえも スカラーの距離が不変であることを意味している。
もちろん スカラー距離は リーマン空間とミンコフスキー空間両方に共通の値である。
このページに示したように 自由粒子のエネルギー (E) と 運動量 (=p) のスカラー距離は 次のように 静止質量エネルギーに関係している。
( もちろん、この静止質量エネルギーは 一般座標変換でも不変である。)
(Eq.6)
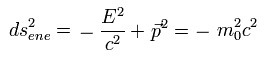
しかし 何か別の外力、例えば電磁気力 (ポテンシャル) などが 自由粒子に作用すると、Eq.6 のスカラー距離は変化する。
つまり、Eq.6 の定常なスカラー距離は 重力のみによるベクトルの変化を意味している。(= クーロン力などの 他の力は存在せず。)
ここで 反変ベクトル V の 平行移動を得ることにする。
(Eq.6-2)
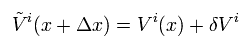
Eq.6-2 と Eq.4 を Eq.5-2 に代入して、
(Eq.6-3)
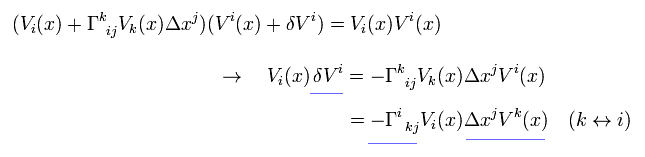
ここでは 2次の無限小を無視した。
結果的に 反変ベクトルの平行移動は、
(Eq.6-4)
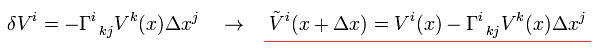
g(x+Δ) を展開すると、
(Eq.7)
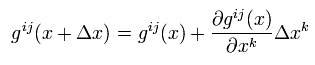
Eq.4 と Eq.7 を Eq.5 に代入して、
(Eq.8)
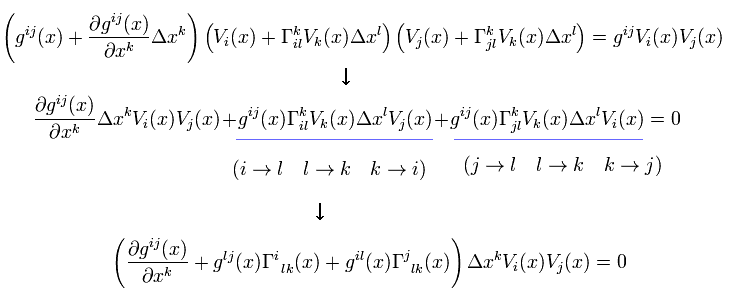
ここで Δx の2次の項を無視した。
( 縮約する 2つの添え字の記号は自由に変えることができる。 ex. i i → k k )
Eq.8 は 任意の Δx と V で成り立つ。 そのため次を得る。
(Eq.9)
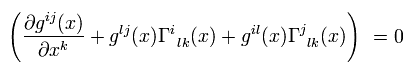
クリストッフェル記号が次を満たすと仮定する。
(Eq.10)
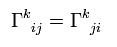
ここで 次の関係式を証明する。
(Eq.11)
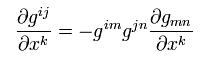
計量テンソルは次を満たす。
(Eq.12)
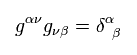
Eq.12 より、
(Eq.13)
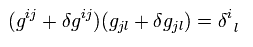
δg の2次の項を無視して、
(Eq.14)
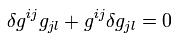
Eq.14 に grl をかけて、
(Eq.15)
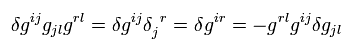
次のように添え字を変えて、
(Eq.16)
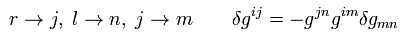
Eq.11 を証明できた。
Eq.9 の2項目は、
(Eq.17)
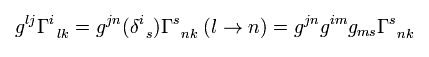
また Eq.9 の3項目は、
(Eq.18)
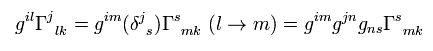
Eq.11、 Eq.17、 Eq.18 を Eq.9 に代入して、
(Eq.19)
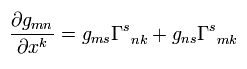
ここで 次を定義する。
(Eq.20)
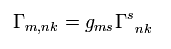
Eq.19 は、
(Eq.21)
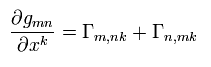
Eq.21 の添え字を変えて、
(Eq.22)
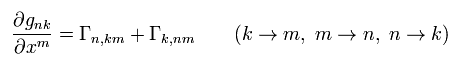
同様に、
(Eq.23)
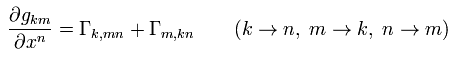
( Eq.21 + Eq.22 - Eq.23 )/2 は、
(Eq.24)
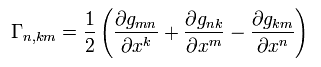
ここで Eq.10 を使った。
次の関係式を用いて、
(Eq.25)
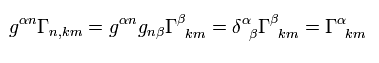
Eq.24 は、
(Eq.26)
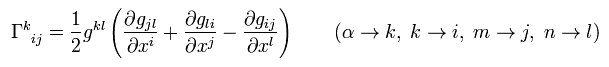
よって クリストッフェル記号を 計量テンソル g を用いて表わせた。
すでに述べたように これらのクリストッフェル記号や計量テンソルgは その地点における重力と関係している。
このページで述べたとおり、一般相対論では 共変形式に合わせるために たくさんの人為的な定義があると言っていい。
もちろん 一般相対論の式は ほとんどが解けない。
非常に単純化した近似や 非常に小さな効果だけから 一般相対論を全面的に信じることは難しい。
無視できるほどの小さな効果よりも ダークマターなどの ビックな矛盾について考慮するのが先であろう。
上で述べたように チルド Vi (x+Δ) は 計算を楽にするためには 共変ベクトルである必要がある。
一般座標変換のもとで (= "一般化された" ローレンツ変換 ), この チルド V は次のように変化する。
(Eq.27)
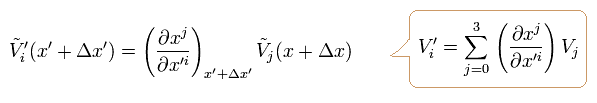
ここで次の関係式を使う。
(Eq.28)
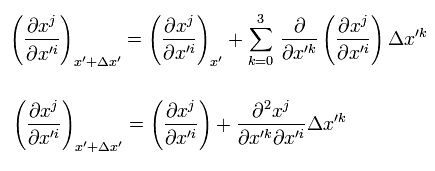
Eq.4 と Eq.28 を Eq.27 に代入して、
(Eq.29)
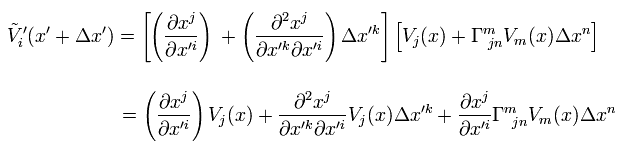
Δx の2次の項を無視した。
次の関係式を使うと、
(Eq.30)
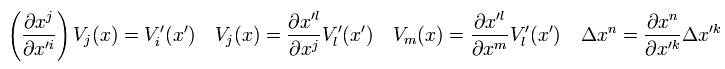
Eq.29 は、
(Eq.31)
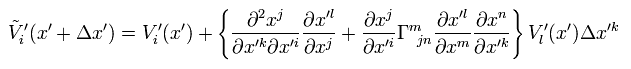
Eq.4 のように、
(Eq.32)
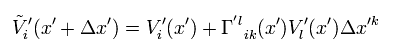
Eq.31 が Eq.32 に等しいことを考慮して、次を得る。
(Eq.33)
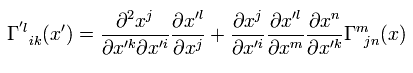
お気づきのとおり、 Eq.33 の第2項目のみが残ったとしたら、 このクリストッフェル記号は 3階の混合テンソルとして変化する。
これはつまり クリストッフェル記号はテンソルでないことを意味している。 (= 共変や反変ベクトルではないということ。 )
また Eq.4 の チルド V を 共変ベクトルにするには、クリストッフェル記号は 一般座標変換のもとで Eq.33 のように変化しなければならない。
Eq.3 を 次のように共変微分として定義する。
(Eq.34)
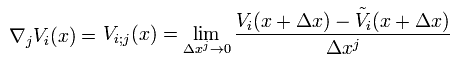
Eq.5 や Eq.6 で述べたように、 もし重力のみ存在するとしたら、 Eq.34 はゼロになる。
つまり、Eq.34 は リーマン時空間における 重力以外の外力による変化を意味している。
Eq.4 を Eq.34 に代入して、
(Eq.35)
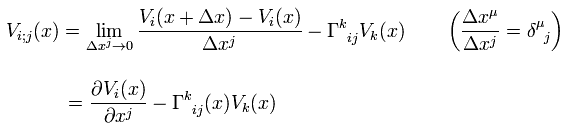
Eq.35 を 共変ベクトル Vi(x) の 共変微分 と呼ぶ。
Eq.6-4 から、反変ベクトル Vi(x) の 共変微分は、
(Eq.35-2)
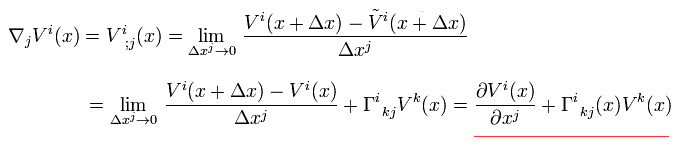
Eq.35 は 2階の共変テンソルとして変化する。
なぜなら チルド V を共変ベクトルにするために Eq.27 を定義したからである。
( もちろん、 V や Δx は 最初からベクトルである。 )
また通常の微分と違い Eq.34 の共変微分の分子の ベクトル V(x + Δx) と "チルド V(x + Δx)" は 同一地点 (= x + Δx ) に存在する。
そのため 共変微分は 位置の変化による ( x → x+Δx ) 座標変換の変化を考慮する必要がなく、Eq.1 の第1項目のような項が現れないため、テンソルとなる。
ここで 実際に Eq.35 が 2階の共変テンソルであることを計算して確かめる。
Eq.1 と Eq.33 を用いると、 Eq.35 は 一般座標変換のもとで 次のように変化する。
(Eq.35-3)

ここでは 次を使っている。
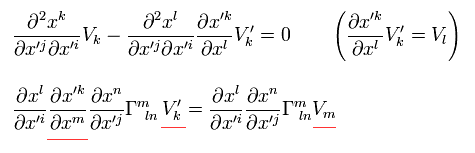
最後の項では、" n " を " l " に交換して、かつ " n " を " k " に置き換えた。
次に 2種類のベクトル A と B が次を満たすことを証明する。
(Eq.36)
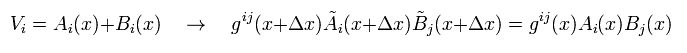
Eq.36 の V=A+B を Eq.5 に代入して、
(Eq.37)
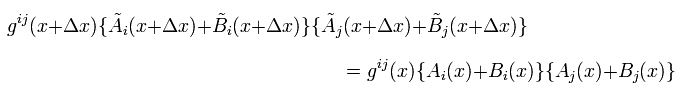
次の関係式を使うと、
(Eq.38)
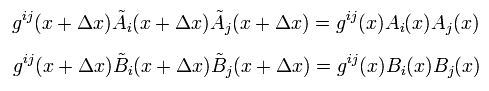
Eq.36 を証明することができた。
次の関係式を使うと、
(Eq.39)
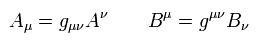
Eq.36 は 次のように表せる。
(Eq.40)
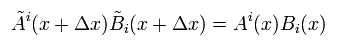
( 定義: gij = gji )
Eq.6-4 で述べたように、反変ベクトルは 平行移動で次のように変化する。
(Eq.44)
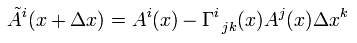
よって 反変ベクトル A の共変微分は、
(Eq.44')
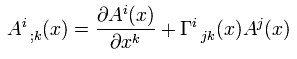
次に 混合テンソル ( 反変 A + 共変 B ) の平行移動を考える。
(Eq.45)
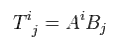
Eq.4、 Eq.44 を使うと、 Eq.45 は次のように変化する。
(Eq.46)
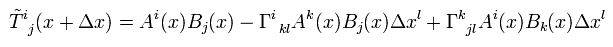
ここで添え字を変えて、 Δx の2次の項を無視した。
次の関係式を使うと、
(Eq.47)
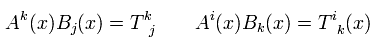
Eq.46 は、
(Eq.48)
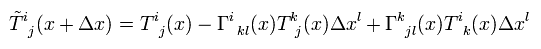
結果的に 混合テンソルは ( Eq.4 + Eq.44 ) のように変化する。
また テンソルの共変微分は、
(Eq.49)
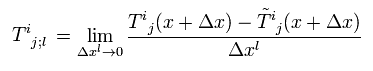
(Eq.50)
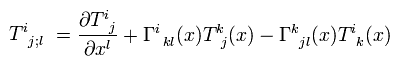
Eq.50 を用いると、計量テンソル g (= 共変 × 共変 ) の共変微分は、
(Eq.51)
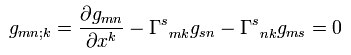
Eq.19 より、 Eq.51 はゼロになる。
反変計量テンソル gij の共変微分もゼロになる。 ( Eq.12 と Eq.51 を使って。 )
(Eq.52)
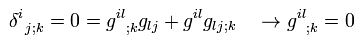
次に 2次の共変微分 ( Δxi と Δxj に関して ) を行う。
Eq.53 の1行目は 共変テンソル ( Am ;i ) の Δxj による共変微分を意味している。 (Eq.51、Eq.50、Eq.35 も参照のこと。)
(Eq.53)
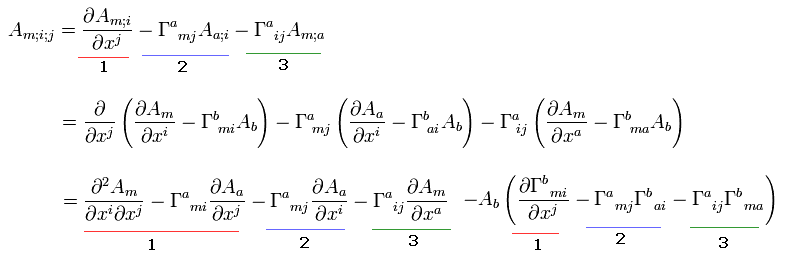
Eq.53 では、Eq.35 や Eq.50 を2回用いて 添え字も適宜 変更している。
各番号 ( 1, 2, or 3 ) は 同じ項由来であることを表している。
共変微分の順序 ( Eq.53 の i と j ) を変えて、片方からもう片方を引き算すると、
(Eq.54)
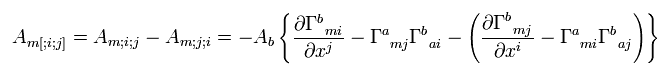
ここでは Eq.53 の最後の行の 5番目と6番目の項のみ残る。
Eq.54 は次のように表せる。
(Eq.55)
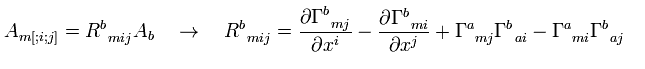
この4階のテンソル R を リーマン曲率テンソルと呼ぶ。
もし このリーマン曲率テンソル R のすべての成分がゼロのとき、 微分は交換可能になり、これはすなわち ミンコフスキー時空間を意味する。
Eq.55 の A が 反変ベクトル Vm のとき、
(Eq.56)
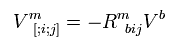
ここで Eq.44' のテンソルの共変微分を用いて、Eq.53 のように計算した。
共変な4階テンソル R は 計量テンソル g × Eq.55 より、
(Eq.57)
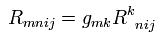
もし 座標変換によって x 地点で 局所慣性系 (= 局所ミンコフスキー空間) に移ると、Eq.24 と Eq.26 のクリストッフェル記号 Γ は ゼロ になる。( x 地点で g = η, Γ = 0 ).
そのため g (= η = x 地点の g ) の 1次の微分と Γ が 局所慣性系である x地点において ゼロになる。
しかし g の2次の微分はゼロでない可能性もある。
この場合 (= 局所ミンコフスキー ) において、 Eq.57 のリーマン曲率テンソルは ( Eq.55 と Eq.26 を用いて )
(Eq.58)
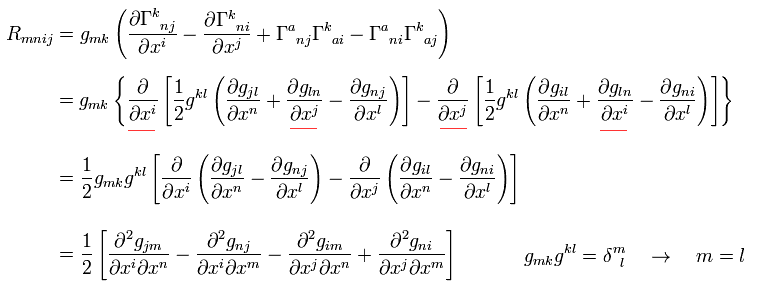
Eq.58 の2行目で、 赤い線の2つの項が互いに打ち消しあう。
そして g の2次の微分が残る。
Eq.58 から、 次の関係式を証明できる。
(Eq.59)
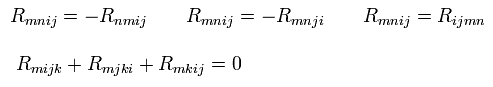
そして 座標変換で リーマン時空間に戻ると、
(Eq.60)
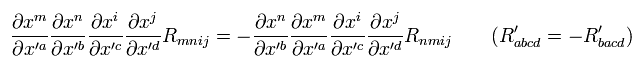
Eq.60 は Eq.59 が すべてのリーマン時空間で成り立つことを意味している。 なぜなら R はテンソルだからである。
Eq.55 の リーマン曲率テンソル の 最初と3番目の添え字 (= i i ) を縮約 (= 0 から 3 まで足す ) すると、
(Eq.61)
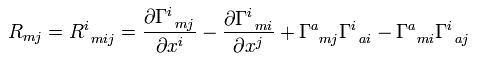
Eq.61 は リッチテンソルという。
リッチテンソルは次のように 対称 Rij = Rji である。
(Eq.62)
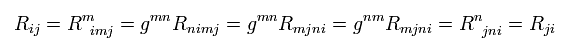
ここで Eq.59 を使った。
さらに リッチテンソルを縮約して、
(Eq.63)
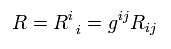
これを スカラー曲率 という。
次の関係式を証明する。
(Eq.64)
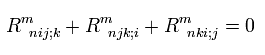
Eq.64 は ビアンキの恒等式という。
Eq.64 は5階のテンソルである。つまり Eq58 から Eq.60 のように、 もし Eq.64 の局所慣性系で関係を証明できたら、 Eq.64 は 一般化されたリーマン空間でも成り立つことになる。
局所慣性系では、 クリストッフェル記号 (= g の1次導関数 ) は局所的にゼロである。
( gの2次導関数はゼロでないかもしれない。 )
つまり Eq,55 より、
(Eq.65)
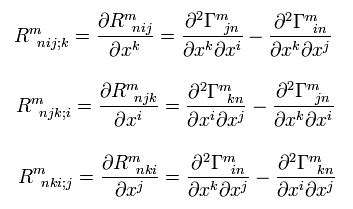
Eq.65 の3つの式を足すと、 右辺はゼロになり、 Eq.64に等しくなる。
Eq.64 に 計量テンソルgをかけて、
(Eq.66)
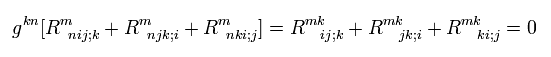
Eq.51 と Eq.52 に示したように、 計量テンソル g の共変微分はゼロである。
そのため g は定数のように扱えて、共変微分の中に入れることができる。
そして Eq.66 で j を m に変えて、 m に関して縮約すると、
(Eq.67)
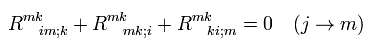
Eq.67 の2項目は、スカラー曲率 (= Eq.63) の共変微分であり、 1、3項目は同じである。 ( 添え字を変えて ),
(Eq.68)
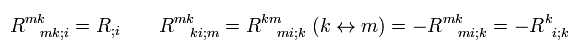
ここで Eq.59 を使った。
Eq.68 より、 Eq.67 は、
(Eq.69)
 この G は アインシュタインテンソルという。
この G は アインシュタインテンソルという。
お気づきのとおり、 Eq.69 は 電磁場などの エネルギー運動量テンソルの関係に似ている。
共変な2階のアインシュタインテンソルは、
(Eq.70)
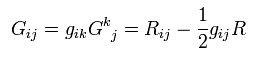
よって、共変な2階のアインシュタインテンソルの発散もゼロとなる。
(Eq.71)
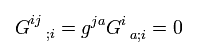
すでに述べたように、 計量テンソル g は共変微分で定数のように扱える。
Eq.69 のアインシュタインテンソルを縮約して、
(Eq.72)
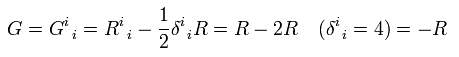
Eq.72 を Eq.70 に代入して、
(Eq.73)
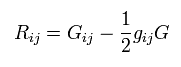
リッチテンソルはアインシュタインテンソルで表せる。
計量テンソル g の行列式は 余因子 Y を用いて表すことができる (= 余因子展開 )。
(Eq.74)
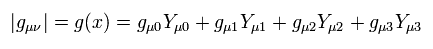
ここで
(Eq.74-2)
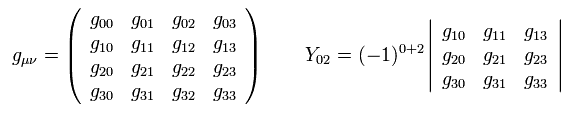
ここで Y の μ は 単なる記号として扱い それに関して縮約は行わない。
g の逆行列は、
(Eq.75)
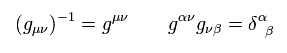
Eq.74 を部分積分して Eq.74 に Eq.75 をかけて δ 関数にすると、
(Eq.76)
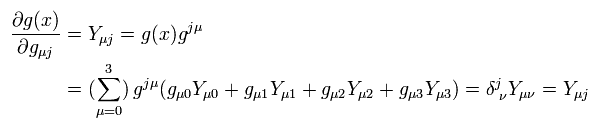
Eq.76 から、次の重要な公式を得る。
(Eq.77)
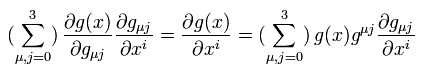

2012/4/12 updated This site is link free.