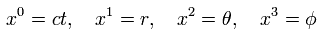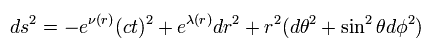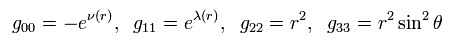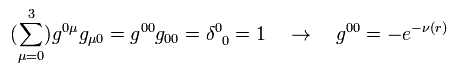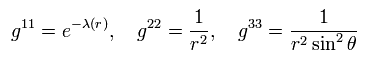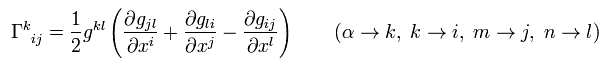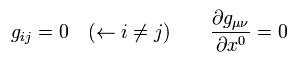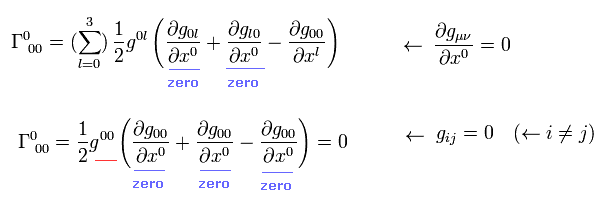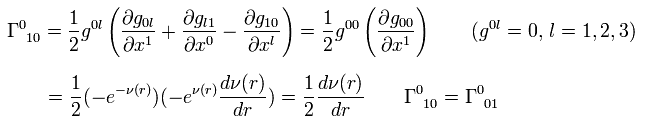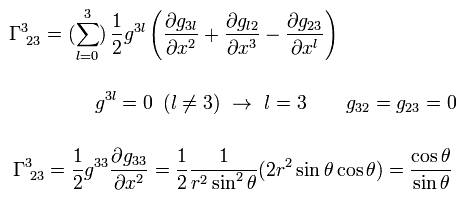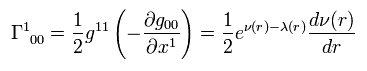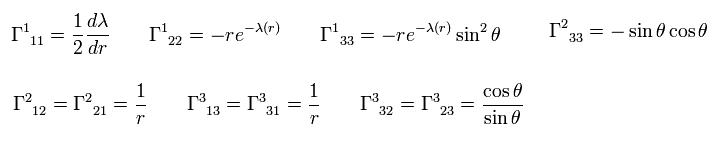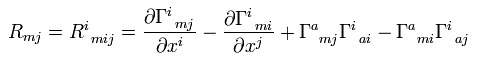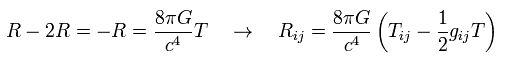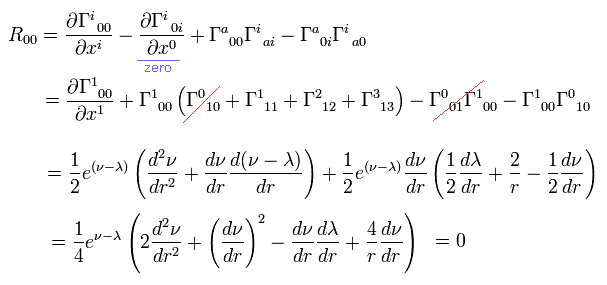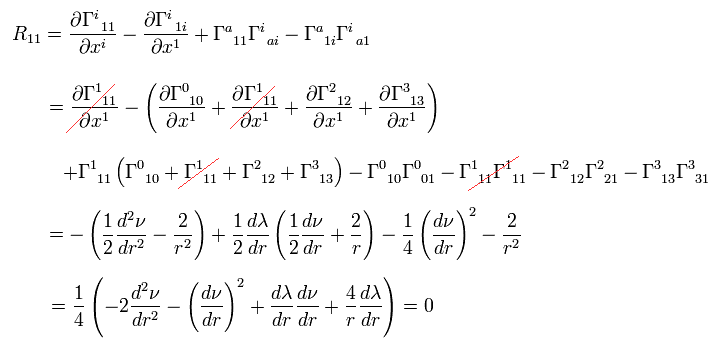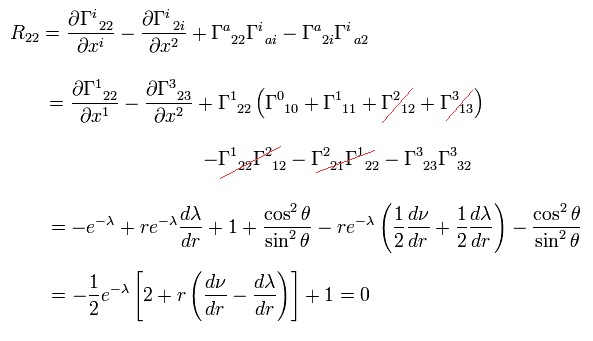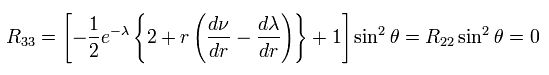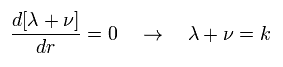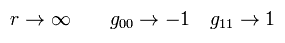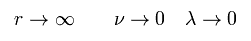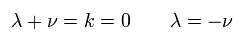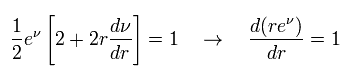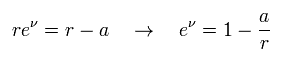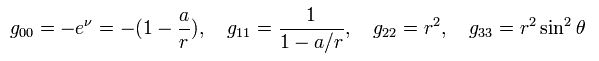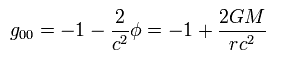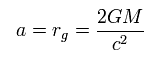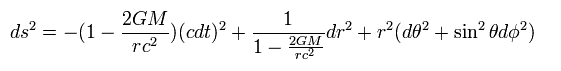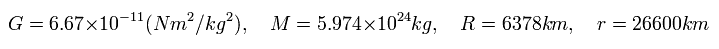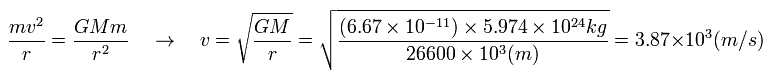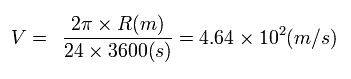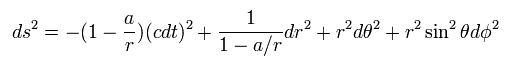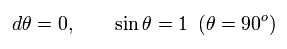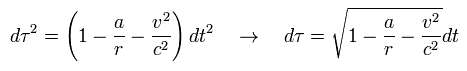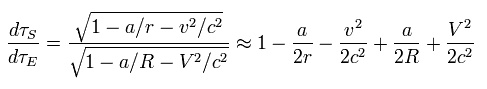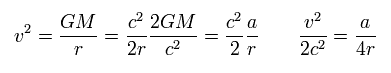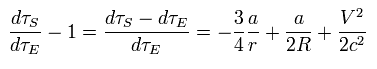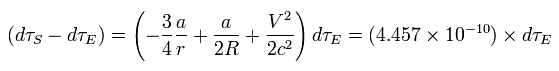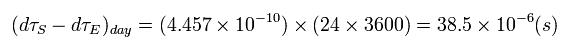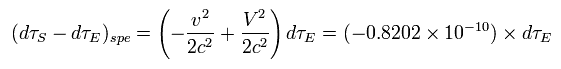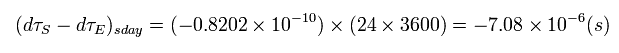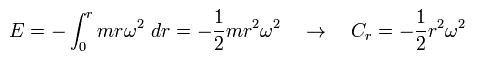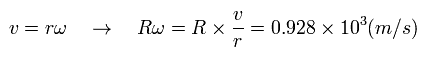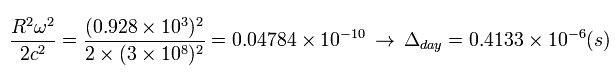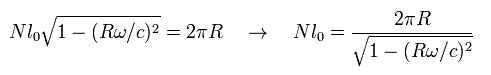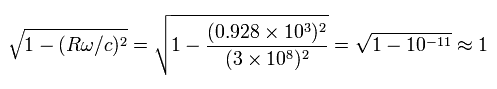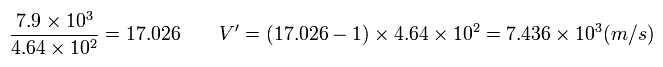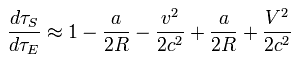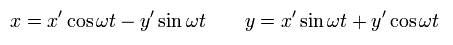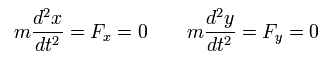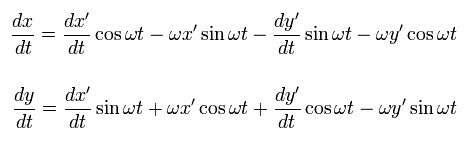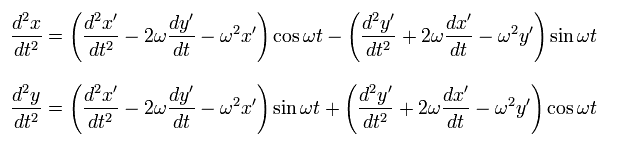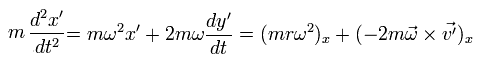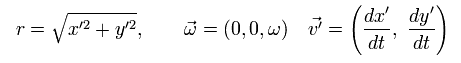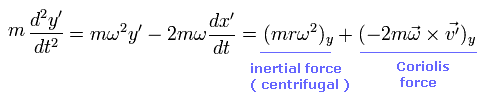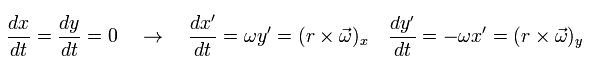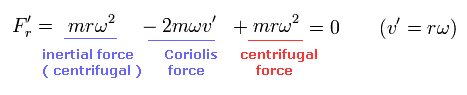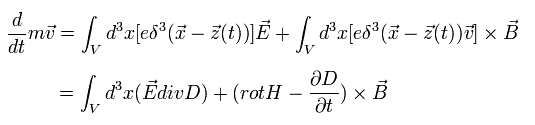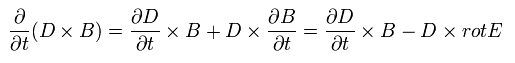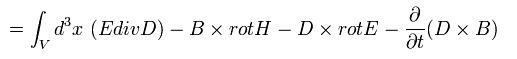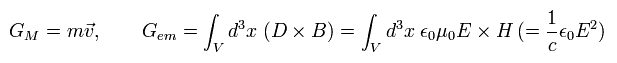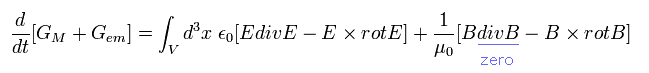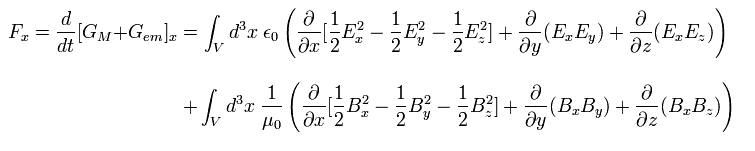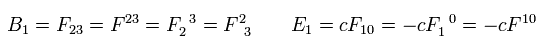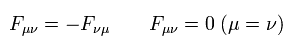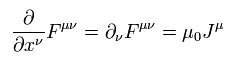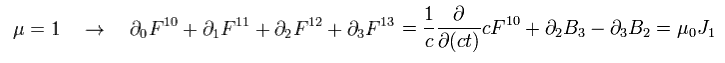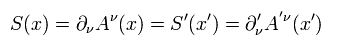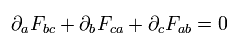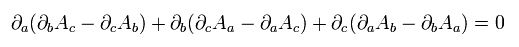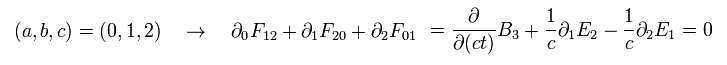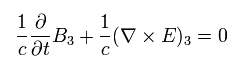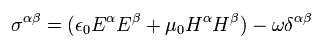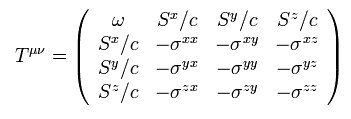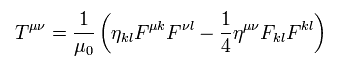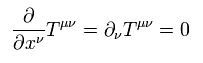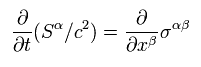GPS 衛星の時計の時間補正は本当に相対論的補正なのか?
トップページ (2電子原子も含む正確な新ボーア模型)
一般、特殊相対論は本当は間違い?
リーマン、リッチ、アインシュタインテンソル。
シュヴァルツシルト解の導出。
このページの Eq.119 まで読んでない方は先にそちらを読まれるように。
シュバルツシルト解 (計量) は 1915 年の アインシュタイン方程式の最初の解であり、 ブラックホールの存在を予言した。
このケースでは 質量 M の点粒子が 原点にあり、 重力場は球対称であり かつ静的 (= 時間微分はゼロ ) としている。
( そのため シュバルツシルトの計量は 最初から地球のようなものを想定していた。 )
極座標を用いて、
(Eq.1)
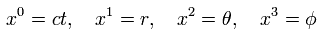
計量テンソル gμν × 各座標は次のように表せる。 ( 球対称を考慮して ),
(Eq.2)
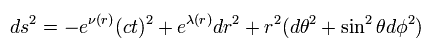
ここで
(Eq.3)
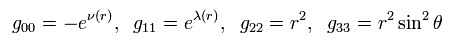
他の計量テンソルはゼロとする。
gμν は 次のように定義してある。
(Eq.4)
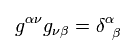
一般的に ミンコフスキー計量テンソルと違い、 gμν は gμν と等しくない。
Eq.3 と Eq.4 より、
(Eq.5)
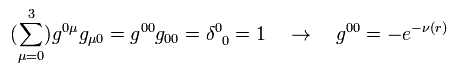
と
(Eq.6)
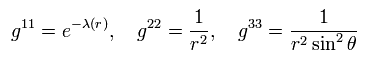
このページに示したように、クリストッフェル記号は、
(Eq.7)
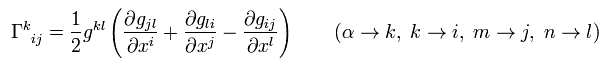
計量 g は 静的で Eq.3 に限定されている。
(Eq.7-2)
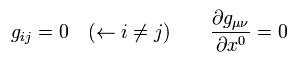
Eq.3、Eq.5、 Eq.6、 Eq.7 より、 次を得る。
(Eq.8)
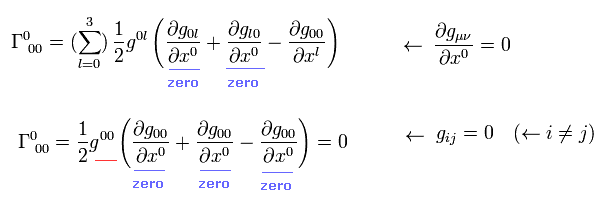
つまり Eq.8 の クリストッフェル記号はゼロとなる。
Eq.8 のように、ほぼすべての クリストッフェル記号は Eq.7-2 の非常に厳しい制限のために ゼロとなる。
同様に、
(Eq.8-2)
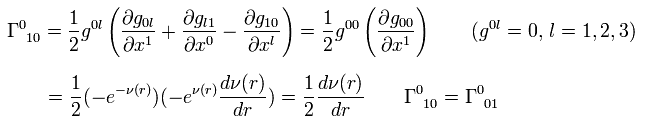
(Eq.8-3)
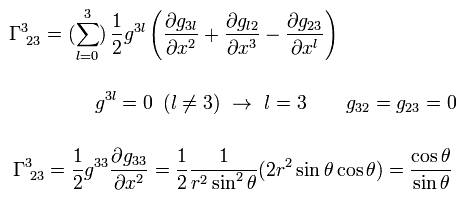
と
(Eq.9)
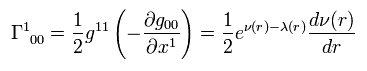
同じように、
(Eq.10)
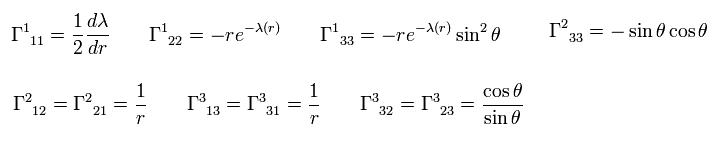
他のクリストッフェル記号はすべてゼロとなる。
リッチテンソルは、
(Eq.11) .
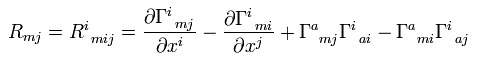
(もし リーマン曲率テンソルの1番目と4番目を縮約したなら、 Eq.11 にマイナス符号をつけるように。 )
このページの Eq.112 に示したように、 リッチテンソルは エネルギー運動量テンソル T を用いて表すことができる。
(Eq.112')
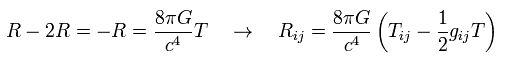
真空では、すべてのエネルギー運動量テンソルはゼロになるため、リッチテンソルも ゼロになる。
( 注意: リーマン曲率テンソルはゼロではない。 )
Eq.8,9,10 と Eq.11 より、次を得る。
(Eq.12)
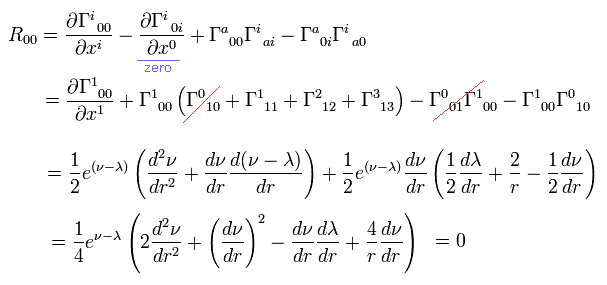
(Eq.13)
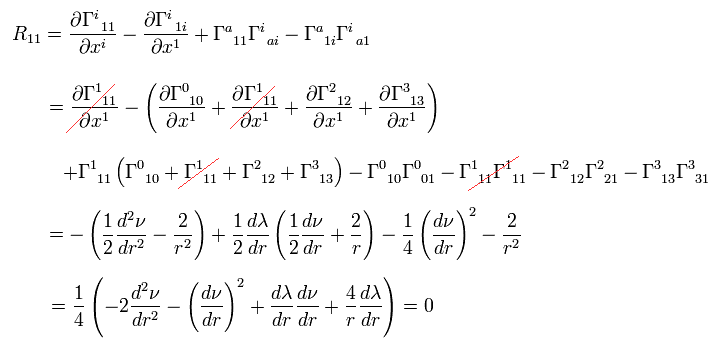
(Eq.14)
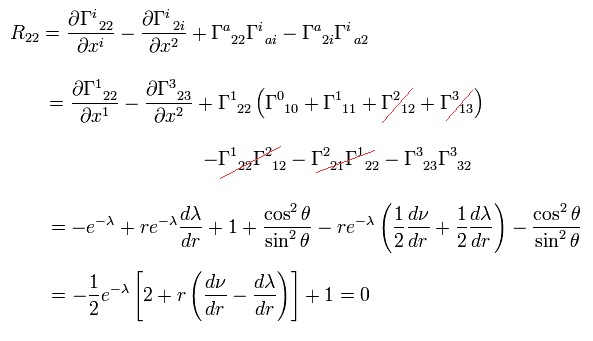
(Eq.15)
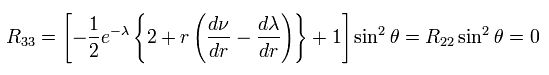
Eq.13 を Eq.12 に代入して、次を得る。
(Eq.16)
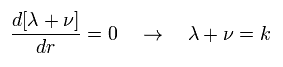
ここで k は 定数である。
r → ∞ の無限遠では、 重力をゼロとする。 (= g がミンコフスキー計量テンソルになる。),
(Eq.17)
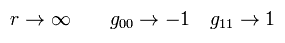
Eq.3 と Eq.17 より、
(Eq.18)
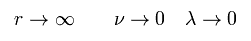
Eq.16 と Eq.18 から 次を得る。
(Eq.19)
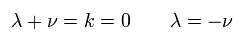
Eq.19 を Eq.14 に代入して、次を得る。
(Eq.20)
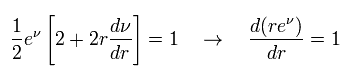
Eq.20 を積分して、
(Eq.21)
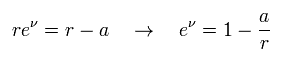
ここで a は定数である。
Eq.21、 Eq.19、 Eq.3 より、 各計量テンソルは、
(Eq.22)
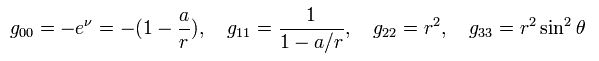
このページの Eq.124 ( Eq.107 ) に示したように、 これは ニュートン力学の重力ポテンシャル φ(r) = -GM/r にマッチしなければならない。
つまり g00 は 次のようになる必要がある。
(Eq.124')
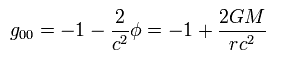
Eq.22 と Eq.124' から、 "a" は 次に示す "シュヴァルツシルト半径" を意味する。
(Eq.23)
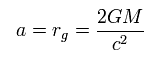
結果的に、 Eq.2 は 次の シュヴァルツシルト解となる。
(Eq.24)
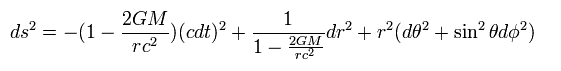
GPS 衛星の時計は本当に相対論効果を示すのか?
ここで 次の値を用いる。
(Eq.25)
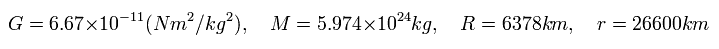
ここで G は "重力定数"、 M は 地球の質量。
R は 地球の半径、 r は 地球の中心から 人工衛星までの距離である。
衛星の遠心力が重力と等しいとすると、
(Eq.26)
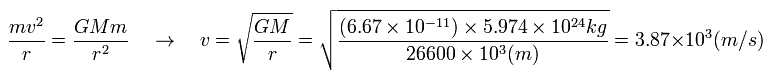
Eq.26 の v は 衛星の速度である。 (静的な地球に対する。)
地球は1日1回転することを考慮すると、 地球上のある地点における速度 V は、
(Eq.27)
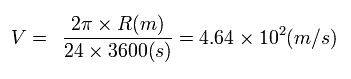
ここで 分母は 1 日の秒数を表している。
Eq.23 と Eq.24 より、
(Eq.28)
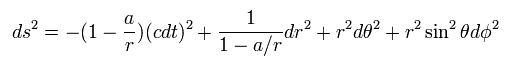
ここで 地球と衛星の距離 r が 一定とする ( dr = 0 )。 また 次の条件を満たすように回転しているとする。
(Eq.29)
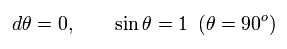
このページの Eq.89 に示したように、 ローレンツ不変なスカラーである 固有時 (= τ ) と Eq.29 を用いて、
(Eq.30)

Eq.30 から、固有時の変化は、
(Eq.31)
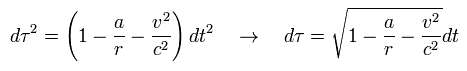
Eq.31 を使うと、 衛星の時間 (= τS ) と 地球上の時間 (= τE ) の 比は、
(Eq.32)
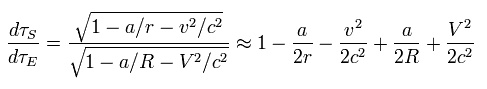
Eq.26 と Eq.23 から、
(Eq.33)
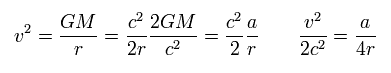
Eq.33 を Eq.32 に代入して、
(Eq.34)
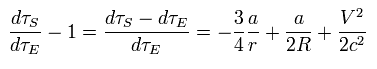
ここで、
(Eq.35)

つまり 地球のシュヴァルツシルト半径は わずか 0.9 cm となる。
Eq.25、 Eq.27、 Eq.34、Eq.35 から、 次の関係式を得る。
(Eq.36)
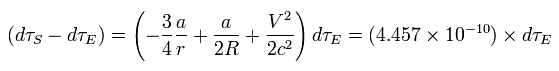
つまり 衛星の時計は 地上の時計に比べて 1日あたり次の時間 速くすすむことになる。
(Eq.37)
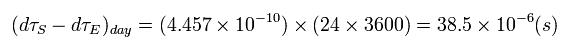
よって 一般と特殊相対論の効果による時間補正は 1日あたり 38 マイクロ秒ということになる。
Eq.32 から 特殊相対性理論の効果のみを抜き出すと、
(Eq.38)
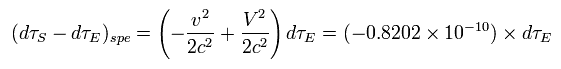
つまり 特殊相対論のみ考慮すると、衛星の時計は 1日に 次の時間だけ 遅くなる。
(Eq.39)
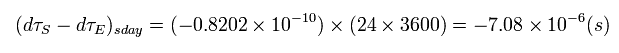
これはつまり、一般相対論のみ考慮すると、衛星の時計は 1日に 38+7 = 45 マイクロ秒 速く進む。
衛星における 双子のパラドックス。
双子のパラドックスは相対論における思考実験の1つである。 双子の1人 (= B ) が 高速のロケットに乗り 宇宙空間へ旅にでて戻ってきたとき、固有時の進みが遅いため スタート地点に残った もう一人の A が自分より老けてしまうことになる。
しかし これを B の視点から見れば、高速で 動いているのは A の方になるため、Aのほうが時間の進みが遅くなり 結果 B のほうが老けてしまうというパラドックスである。
(Fig.1) ふたごのパラドックス。
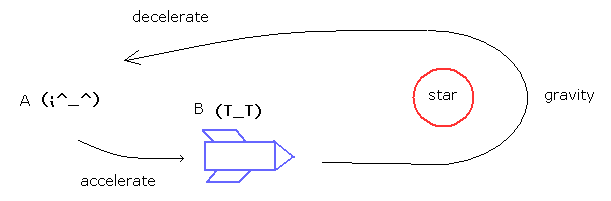
通常の教科書では、B のほうは 宇宙空間に飛び立つのに加速し、Uターンするのに 星の重力などで加速され、最後に元の位置に戻るときに減速するので、B のほうだけ 加速の影響で 時間の進みが遅くなるので パラドックスでないと説明している。
しかし、上の章の GPS の場合はどうであろうか??
人工衛星からの視点では、地上の地点のほうが 衛星よりも 速く動いている。
( これはつまり 上の 特殊相対論による補正が真逆になることを意味する。)
そのため 衛星から見ると 衛星の時計は 1 日に 45 + 7 = 52 マイクロ秒 速く進むことになってしまう。
よって 衛星の時計の自動補正を 1日 38 マイクロ秒でなく 52 マイクロ秒にしなければならなくなる。
これは パラドックスである。
もちろん、通常の 双子のパラドックスと異なり、すでに 重力の影響は盛り込んである。
また 衛星は接線方向へ動くため、地球との距離 r は固定のため r や R は ローレンツ収縮しない。
つまり 通信シグナルの到達時間は同じである ( t = (r-R)/c. )。
また この人工衛星はコンスタントに速度 v で動いており 止まったりはしない。
正確な値を得るには 衛星の時間補正で コンスタントに 1日 特殊相対論の補正 (= 7 マイクロ秒) をしなければならないことになっている。
よって この相対論効果による衛生の時間補正は不合理であると思われる。
また、このページ (= 全電荷量の保存の破れ ) と このページ (= 直角レバーのパラドックス) に示したように、相対論には 他に致命的なパラドックスが存在する。
重要な点は これらの補正は 1 日に 38 マイクロ秒という 非常にわずかな量ということである。
そのため、大気中のシグナル電磁波の速度の変化や、地球の周りの 誘電体など 他の要因の影響を受けやすい。
また 上の シュバルツシルト解の計算なども はっきり言って 単なる”近似”である。
つまり 上の GPS の時間補正の結果のみから 相対論が正しいとは言えないということである。
地球の周囲に "実在のエーテル" があるとしたら、そのエーテルや 他の誘電体などは 地球に近づくほど 凝集傾向になるだろう。
( GPS では 放射された電磁波の振動数をもとにした 原子時計を使用している。)
例えば、ヘリウム内の音速は 通常の空気内の音速に比べてかなり速い。なぜなら ヘリウムが 空気より軽いためである。
空気内の分子が 重くなるほど、その空気を振動させるのに より時間がかかるからである。
遠心力も含めた 双子のパラドックス。
(Fig.2) 地球の周囲を回る人工衛星 (= B )
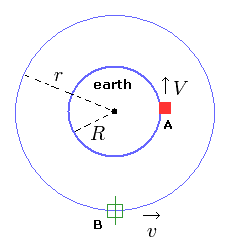
一般相対性理論によれば、回転座標系からの視点だと、遠心力も重力のように扱う必要がある。
この場合は、重力ポテンシャル ( φ = -GM/r ) のように、次のような 遠心力ポテンシャル (= Cr ) を導入する。
(Eq.40)
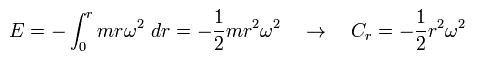
ここで r は 半径、 ω は 角振動数である。
( もちろん、遠心力ポテンシャルが 本当に "時間の遅れ"を引き起こすかどうかは非常に疑わしいが。)
上記のセクションの状況では、地球上の物体 (= Fig.2 の A ) が1日に1周する間に、人工衛星は地球の周りを2周する。
この人工衛星 ( Fig.2 の B ) からの視点では、地球上の物体は逆方向に1周 (= 2-1=1 ) することになる。
この人工衛星に対して静止した 回転座標系では、地球上の物体の速度は 方向は逆だが Eq.27 の元の V と等しくなる。
人工衛星の角振動数 ω を使用して、
(Eq.41)
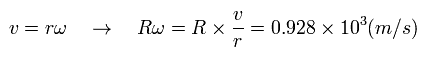
Eq.41 を用いて、 周回する衛星 (= B ) からの視点では、Eq.32 は次のように変化する。
(Eq.42)
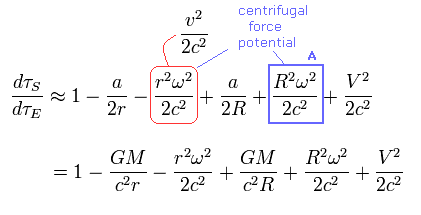
Eq.42 と 上記セクションの Eq.32 を比較すると、
(Eq.32)
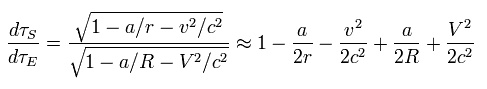
周回する衛星からの視点では、人工衛星の時計の時間が 実験系 (= 全体の静止系) よりも速くすすむことになる。
その時間の差は Eq.42 の A の項にあたる。
基本的に、観測者の視点に応じて 物体それぞれの 時計の固有時間が変化することはあってはならない。
つまり、これは完全に パラドックスである。
Eq.41 を用いると、 この時間差は、
(Eq.43)
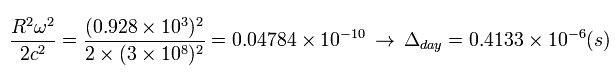
つまり パラドックスの時間差は 1日 0.4 マイクロ秒になる。
この値は小さいが 日に日に 矛盾は大きくなっていく。
---------------------------------------------------------------
回転座標系からの 1周の軌道長はわずかながら 長くなる。
人工衛星からみた 地球1周の長さを N × l0 とする。
ここで l0 は 短い棒1つの長さで、 地球の周囲にこの棒が N 個並べてあるとする。
全体の静止系からみると、各棒は ローレンツ収縮している。一方 半径 R は収縮していない。
そのため、周回する衛星からの視点では、地球の周囲の長さ (= N l0 ) は 次のように見える。
(Eq.44)
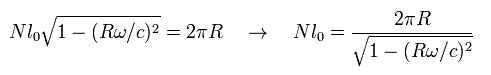
これは 衛星から見ると、 地球1周の長さが 2π R よりも わずかに長くなる。
( このページも参照のこと。 )
しかし、この効果は無視できるほどである。なぜなら、
(Eq.45)
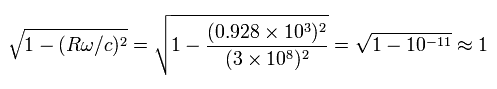
もちろん、この Eq.45 の効果も考慮すれば、Eq.42 の V が少し大きくなるため、 パラドックスの時間差はさらに大きくなる。
----------------------------------------------------------------
[ 地球すれすれを周回している人工衛星。 ]
このパラドックスは 人工衛星が 地球すれすれを運動しているとき ( r = R ) さらに顕著になる。
Eq.26 (= 遠心力が重力につりあう ) より、 この場合の衛星の速度 v は、
(Eq.46)

Eq.46 の速度のとき、この衛星は 1日に地球の周囲を 約17周する。
つまり、この衛星からの視点では、地球上の物は 1日 17-1 = 16 周することになり、その速度 V' は、
(Eq.47)
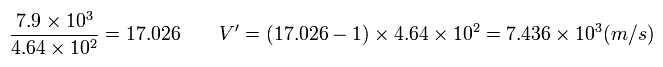
Eq.32 のように、全体の静止系からでは、地球と衛星の間の時間差は、
(Eq.48)
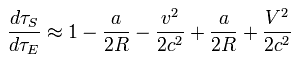
ここで r = R で、 v と V (= Eq.27 ) は それぞれ 衛星と地球上の物体の速度を表す。
Eq.27、 Eq.46、 Eq.47 を用いて、 衛星からの視点では、 Eq.48 は次のように変化する。
(Eq.49)
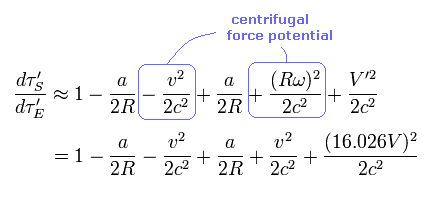
Eq.48 と Eq.49 より、 1日あたりの パラドックスの時間差は、
(Eq.50)

つまり 地球すれすれの衛星の場合は このパラドックスの時間差が 1日に何と 57マイクロ秒にもなる。
これはすなわち GPSの時間補正に 特殊相対論的補正は 正確に使用できないことを意味している。
結果的に GPS の時間は 相対論的効果を意味していない。
(Fig.3) 2つの似た衛星が互いに逆方向を同じ速度で運動している。
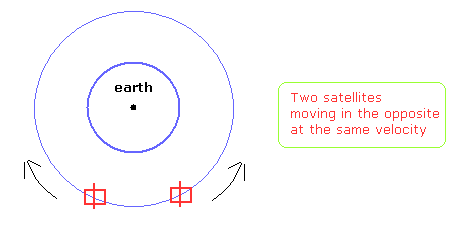
Fig.3 では、2つの似た人工衛星が ほぼ同一軌道上を 同じ逆方向の速度で 周回している。
上記の重力、遠心力ポテンシャルすべてを考慮しても、これは 明らかにパラドックスと自己矛盾を含んでいる。
1つの衛星からの視点では、もう1つの衛星の時計が遅れることになる。
逆の視点からは 相手の時計が遅れることになる。
( 互いにすれすれを横切るとき、互いの時間を伝えあうことができる。)
つまり、GPS の時計補正に特殊相対論的効果が必要な場合は、相対論的効果そのものが間違いということになる。
一般相対論における力とは何か?
(Fig.4) "慣性力" と "抗力" の違いは ?
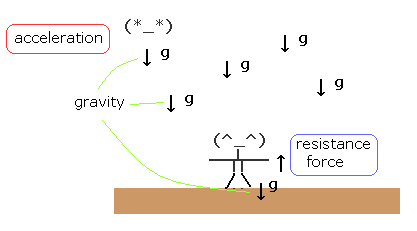
ここでは 重力や 慣性力がなぜ特別扱いされているか説明することにする。
Fig.4 では、1人が地上に立っており、彼は "重力" と 地上からの"抗力" (resistance) を受けている。
これらの2つの力は釣り合っているため、彼は 地上に静止していられる。
もう1人は重力によって落下している (= 自由落下)。
このケースは、一般相対論によれば、自由落下している人は 特殊相対論のみに従い、いわゆるミンコフスキー空間にいることになり、地上の人は 一般相対論に従うことになる。
これらの違いは何なのだろうか?
(Fig.5) ”グローバルな” (= global ) 力 vs. ”局所的な”(= local ) 力。
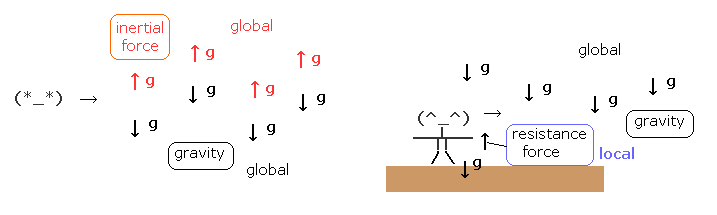
自由落下している人からの視点 (= Fig.5 左 ) では、この世界のすべてのものが 上方向に加速している。
これはつまり グローバルな変化 (= 加速 ) を意味している。
もちろん、重力は この世界の すべてのものに作用している。つまり 重力も "グローバル" な力 (= 加速) なのである。
Fig.5 の左のケースでは、これら 慣性力と重力という グローバルな力 (= 加速) が互いにキャンセルしあうため、ミンコフスキー空間となる (= グローバルな力がゼロ )。
一方、地上に立っている人からの視点では (= Fig.5 の右 )、グローバルな力は 重力の1つしかない。
地面からの抗力は 立っている人にしか作用していない。つまり 抗力は "局所的"な力なのである。
この場合は 彼は ”リーマン空間”を見ていることになる。結果的に "グローバル"な力のみが 世界空間の歪みや 奇妙な ”時間の遅れ”を引き起こすことになる。
[ 遠心力 (ポテンシャル) は、回転系においては "グローバル"な力である。 ]
(Fig.6) S'系 が S静止系に対して 反時計まわりに回転している。.
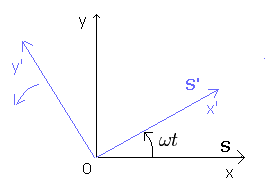
Fig.6 では、 S'の系が S に対して 角速度 ωt で 反時計方向に回転している。
S' からの座標 ( x', y' ) と、S からの座標 ( x, y ) は 次の関係にある。
(Eq.51)
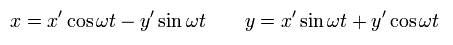
S に対して静止しておりかつ何の力も受けていない物体があるとする。
(Eq.52)
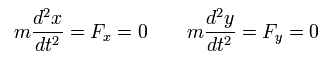
Eq.51 を 時間 t で微分して、
(Eq.53)
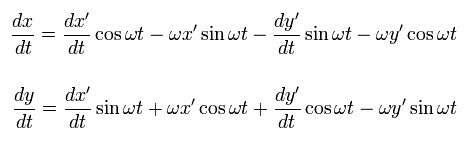
Eq.53 を さらに微分して、
(Eq.54)
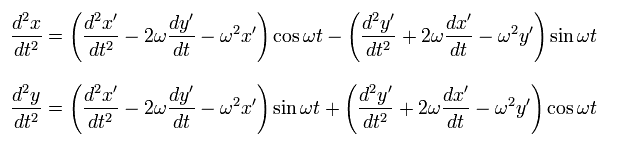
Eq.54 の上の式に cos ωt、 下の式に sin ωt をかけて、それらを足し合わせると、Eq.52 の条件のもとで、
(Eq.55)
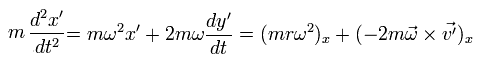
ここでは、
(Eq.56)
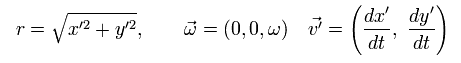
同じように、Eq.54 の上の式に -sin ωt、 下の式に cos ωt をかけてそれらを足すと、Eq.52 の条件のもとに、
(Eq.57)
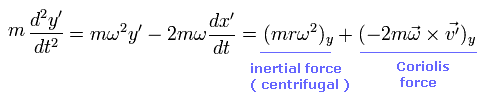
Eq.55 と Eq.57 では、最初の項は 遠心力由来の慣性力 (inertial force) を表し、2つめの項は コリオリ力を表している。
重要な点は、慣性力 (= 遠心力) は、位置変数のみの関数だということである。
すなわち この世界のすべての物は この慣性力を受ける。よって "グローバル"力である。
この位置変数に関して、この慣性力 (遠心力)は、位置エネルギー (= 遠心力ポテンシャル) を生じることになる。これは上のセクションで説明した。
一方、コリオリの力は 速度のみに関係しており、かつこの速度に対して垂直な方向である。
つまり、ローレンツ力の磁気力のように、コリオリ力は ポテンシャルエネルギーとは関係ない。
S 系に対して静止している物体を S' の回転系からみると、次の速度で運動している。
(Eq.58)
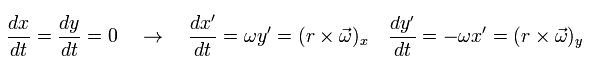
これは S' から見ると、この物体は 速度 rω で 時計方向に回転している。
もちろん、この物体は S 系に対して静止しているため、S' から見ても 動径方向の力はゼロにならなければならない。
Eq.55、 Eq.57、 Eq.58 を考慮すると、 S' 系からの動径方向の力は、
(Eq.59)
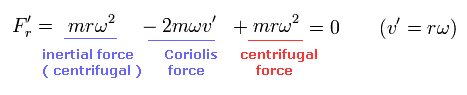
Eq.59 の最初の項は グローバルな "慣性力" を意味しており、これは系全体の回転から生じる。
上で述べたように、この力は 遠心力ポテンシャルと関係している。
また 2番目の項が コリオリの力である。
この物体は 速度 rω で運動しているため これに垂直方向に コリオリの力を受けることになる。
そして最後の項が S'系からみた 普通の”遠心力”である (Eq.58 参照)。
結果的に S とS' 系両方からみても 動径方向の力はゼロになる。
電磁場の共変形式。
このセクションは このページから移動してきたものである。
[ 電磁場の運動量の保存。 ]
点電荷 e が ローレンツ力と 電場によって運動しているとき、その運動方程式は、
(Eq.51')
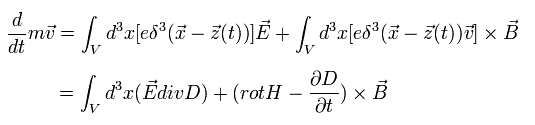
ここで Eq.24 (このページ) の関係式を用いた。 また 電荷の動き (= ev ) を 電流 i と解釈した。
しかし この解釈は間違いである。
このページに示したように、 運動する単一電子の周囲の磁場は 必ず 変動する電場によって表すことができる。
電流 i というのは連続でなければならない。 しかし単一電子は不連続である。
また 我々は 同じ磁場を2回重複してカウントしてはならない。.
ここで 次の関係式を使う。
(Eq.52')
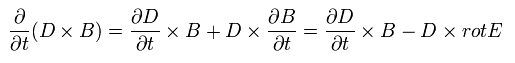
Eq.52' を Eq.51' に代入して、
(Eq.53')
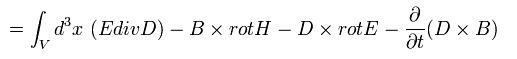
ここで A × B = - B × A.
粒子と電磁場の運動量を次のように定義する。
(Eq.54')
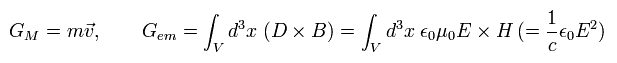
Eq.52'、 Eq.53'、 Eq.54' から 運動方程式は、
(Eq.55')
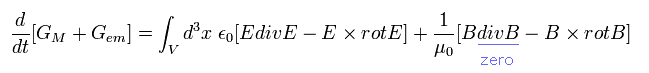
ここで B div B = 0 を追加した。
Eq.55' から、 電磁場の力 F の x 成分は、
(Eq.56')
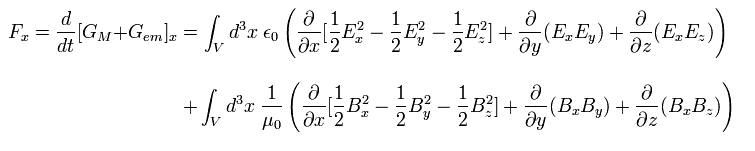
これは 相対論的なエネルギー運動量テンソルに使われている非常に重要な式である。
しかし 真空の電磁場のエネルギー ω がエネルギーでなければ、 Eq.54' は 電磁場の運動量を意味しない。
[ローレンツ不変なマクスウェル方程式。 ]
反対称テンソルを使って、 電磁場の x 成分は、
(Eq.57')
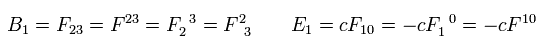
反対称テンソルは次の関係式を満たす。
(Eq.58')
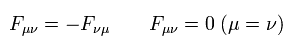
これらの関係式を使うと、マクスウェル方程式は次のように表せる。
(Eq.59')
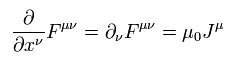
例えば μ = 1 のとき、
(Eq.60')
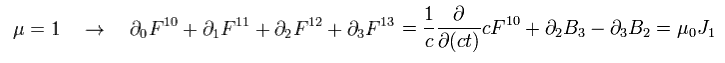
εμ = 1/c2 や Eq.57' を使うと、 Eq.60' はマクスウェル方程式に等しいことがわかる。
すでに述べたように すべての変数 (= x, A and J ) は 4元ベクトルとして変化する。つまり Eq.59' は ローレンツ不変なテンソルとして変化する。
これはつまり Eq.59' のマクスウェル方程式は ローレンツ共変 (= Eq.59' の式の”形”がローレンツ変換で変化しない。)
Eq.59' では、2つのベクトルを縮約している。 ( ν を 2回使っている。 また それらは 反変と共変ベクトルのペアである。),
(Eq.61')
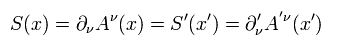
Eq.61' は ローレンツ不変なスカラーである。
また 次の関係を満たす。
(Eq.62')
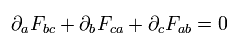
次のように 反対称テンソル Eq.62 に代入すると理解できる。
(Eq.63')
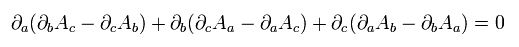
Eq.62' は 残りのマクスウェル方程式を意味する。 例えば、
(Eq.64')
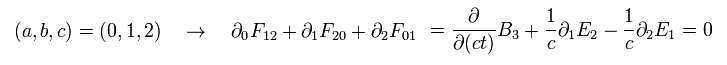
(Eq.65')
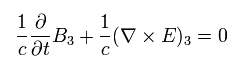
これは 最後のマクスウェルの式である。 もちろん Eq.62' はローレンツ共変なテンソルである。
重要なことは これらの相対論的なマクスウェル方程式は 4元ベクトル の前提条件に完全に依存していることである。
しかし この前提条件は 深刻な問題を引き起こす。
ここで 次を定義する、
(Eq.66')
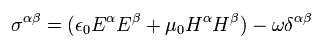
と
(Eq.67')
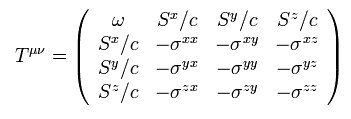
ここで ω と S は 真空のエネルギー と ポインティングベクトル を意味する。
Eq.67' は 次のような ローレンツ共変なテンソルを意味する。
(Eq.68')
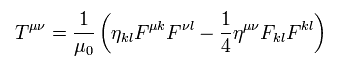
これは 電磁波における エネルギー運動量テンソルと呼ばれるものである。
次の関係式を定義すると、
(Eq.69')
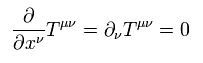
μ = 0 のとき、 Eq.69' は エネルギーとポインティングベクトル と等しい。
また μ = 1, 2, もしくは 3 のとき、
(Eq.70')
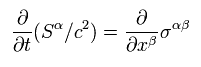
Eq.70' は Eq.56' (= 運動量と力 ) に等しい。
おそらく ベクトルポテンシャル A のいう概念は ローレンツ共変性にマッチするために考案されたものだろう。

2012/5/22 updated This site is link free.