トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。
超ひも理論 vs. ループ量子重力理論。
ゴーストと BRST 変換はリアルなのか?
このページでは、どうして 弦理論の臨界次元が ボソンで 26 次元 ( 超弦理論で 10 次元 ) になるのかを、ゲージ固定と セントラルチャージ(中心電荷)によるアノマリーの視点から説明することにする。
基本的に 経路積分法は 弦理論において 相関関数を考慮するときに重要な概念である。
しかし この経路積分法というのは 調べてもらうとお分かりになると思うが、現実の世界でまったく役に立たない。
なぜなら 最初と最後の途中経路にある すべての変数について 対称性を保つために 無限大から無限大の積分をしなければならないからである。
もし ゲージをどれかに固定すると それによる アノマリー(異常項)が生じる。
その異常項はセントラルチャージという奇妙な数学的な概念と関係しており、対称性を保つために これを除去するのに 何と 26 (もしくは 10) 次元の世界が必要になってくるというわけである。
( しかし、こんな非現実的な余剰次元に頼るぐらいなら、対称性も含めたその前提条件が間違っているという発想には いたらないのだろうか? と思ってしまう。)
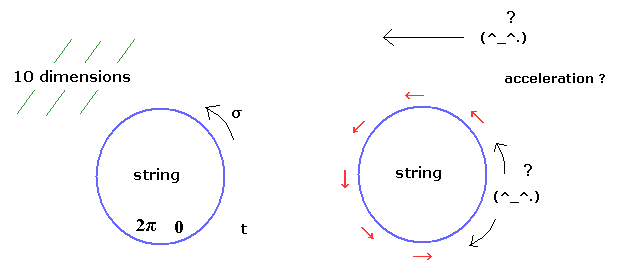
(Fig.1) 超ひもは 現実の”ひも”とは違う。

最初に 世界面上の 空間1次元+時間1次元のひもは実在のものでは表せない。
なぜなら ひも理論は 基本的に 0 から 2π で元に戻る 円形をしており、これを表現するには 少なくとも空間2次元 (x,y) か (r, θ) が必要になってくるからである。
つまり この奇妙な世界面では 物体は ひもの方向に進めない。(このページも参照のこと。)
(Eq.0-1) 数学上のトリック。
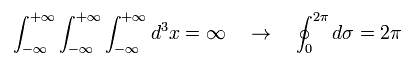
Eq.0-1 に示すように、もし 1次元の人為的なリングを定義すると、Eq.0-1 左の無限大の 空間積分が Eq.0-1 右の 単純な 2π で表すことができる。
また 共形場理論 では、1次元のリングは 閉じた円の複素積分と見なすことができる。
つまり 単に数学上の理由のみのために この 1+1 次元のひもが選ばれたと言っていい。
(Eq.0-2) グラスマン数 "c".
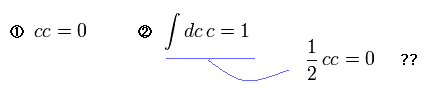
ひも理論の共形場理論では 私達の世界の 非常に重要な次元の数を決定する際に 人為的な グラスマン数を使用している。( このページも参照のこと。 )
Fig.0-2 の "1" の定義は Fig.0-2 の "2" の定義と矛盾している。
( "1" を満たすなら、 "2" はゼロになるべきだが ゼロでない。)
これらの定義は 私達人間による人為的なものであり、自然界の法則そのものを意味していない。
この2次元のひもの位置や大きさ が 標的空間 (= 26 もしくは 10 次元のミンコフスキー背景空間 ) に対して 任意のものをとっても、ひもの運動方程式が変わってはいけない。
つまり この厳しすぎる数学的な対称性のせいで この ひもを実在のもので表現することは不可能である。
このページでは 対称性理論に容易に扱えるように 時間成分をウィック回転した ユークリッド空間を用いる。
つまり ミンコフスキー計量テンソルは次のようになる。
(Eq.1)
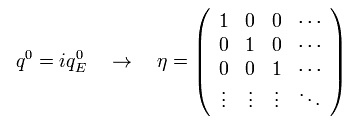
つまり、 ( -1, 1, 1 ..) バージョンの代わりに ( 1, 1, 1, ...) バージョンを用いる。
ある座標変換のもとで、計量テンソル g のスケールが 次のように変わる場合、
(Eq.2)
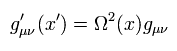
これを "共形変換"という。
次の無限小変換のもとで、(2次の無限小は無視して)
(Eq.3)
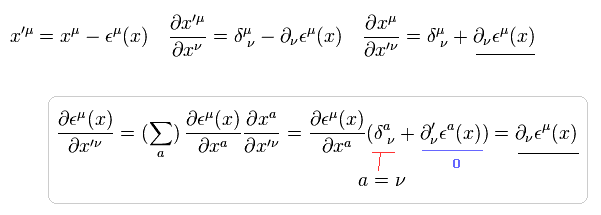
計量テンソルは次のように変化する。
(Eq.4)
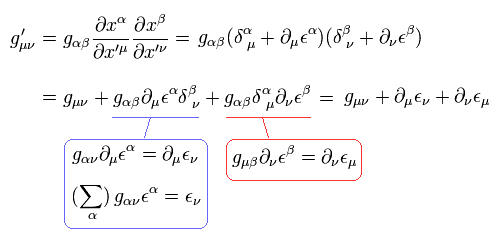
ここでは 次を使った。
(Eq.5)
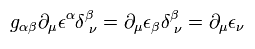
Eq.2 より、 Eq.4 は 次を満たす。
(Eq.6)
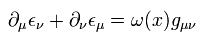
ω の形が A+ Bxμ のような x の一次式のとき、ε は x に関して二次式にならなければならない。
(Eq.7)
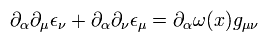
基本的に、並進、回転、スケール変換は 次のように表せる。
(Eq.8)
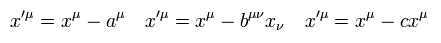
2次元 ( 空間1+時間1 ) の世界面では、ユークリッド空間の計量テンソル g は、
(Eq.9)
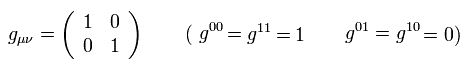
(反変な)計量テンソルは次のように変化する。
(Eq.10)
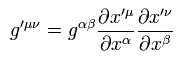
Eq.2 と Eq.9 より、 次の関係式が満たされる必要がある。
(Eq.11')
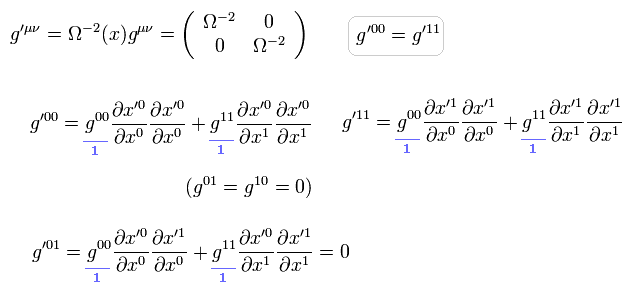
つまり
(Eq.11)
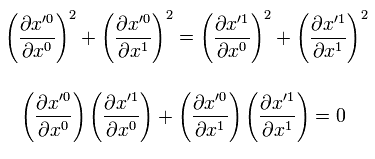
Eq.11 は 次の式を含んでいる。
(Eq.12)
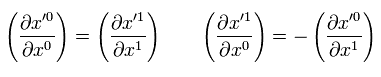
Eq.12 は 次の複素平面における コーシー・リーマンの式に等しい。
(Eq.13)
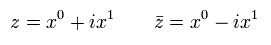
つまり、もし 座標変換後の 複素数 z' が z に関して 微分可能(正則関数)なら Eq.12 は自動的に満たされる。
Eq.13 より、 実数の x0 (= 時間 ) と x1 (= 空間 ) は 次のように表せる。
(Eq.14)
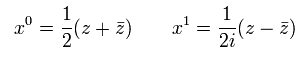
また 微分演算子を次のように定義する。
(Eq.15)
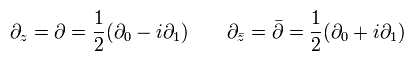
と
(Eq.16)
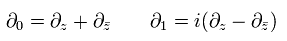
Eq.9 と Eq.13 から、 スカラーの長さは、
(Eq.17)
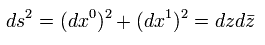
よって、z の計量は、
(Eq.18)
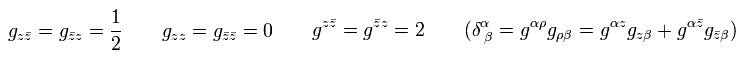
一般的に、共形変換は次のように表せる。
(Eq.19)
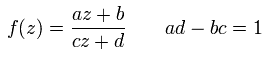
例えば、並進変換は、
(Eq.20)
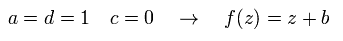
スケール変換や回転は、
(Eq.22)
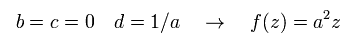
反転は、
(Eq.23)
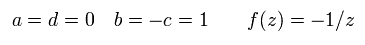
場が次のように変化するとき、
(Eq.24)
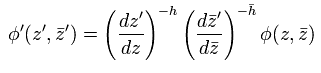
この場を プライマリー場 と呼ぶ。
そして、 "h" を "共形ウェイト" という。
例えば、この変換の 共変テンソル (= bzz) は、
(Eq.25)
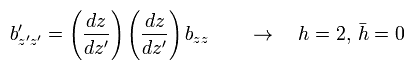
つまり、 "h" に関してウェイトは "2" である。
次に ストレスエネルギーテンソル (エネルギー運動量テンソル) Tμν について説明する。(最初に 4次元空間で。)
ストレスエネルギーテンソルは 様々な座標変換の下での 作用 S の不変性から得ることができる。
次の無限小座標変換のもとで、
(Eq.26)
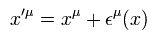
作用 S の変化は、
(Eq.27)
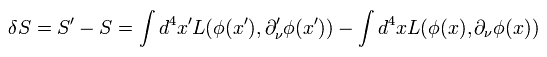
ヤコビアンは 変換のもとでの行列式で表わされる。
(Eq.28)
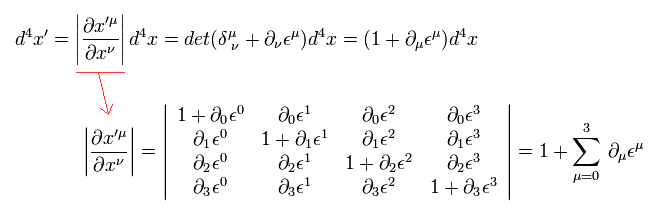
2次以上の無限小は無視している。そのためこれだけ簡潔な表現になる。
ラグランジアン L の変化は、
(Eq.29)
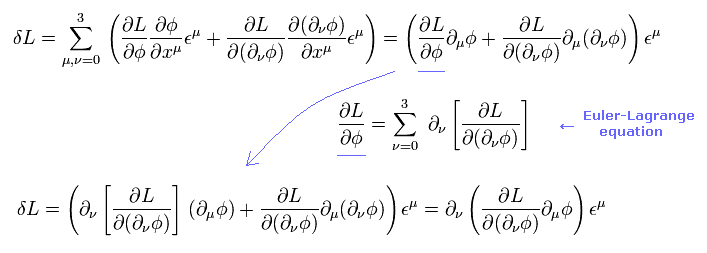
オイラーラグランジュ方程式は、
(Eq.30)
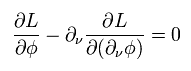
Eq.30 を Eq.29 に代入して、 かつ Eq.27 と Eq.28 を用いると、次を得る。
(Eq.31)
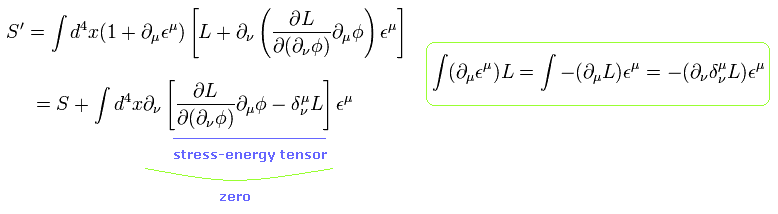
作用 S は 変換のもとで不変なスカラーである。( S'-S = 0 )
結果、ストレスエネルギーテンソルを得ることができた。(この係数は変更できる。)
Eq.13 の z と bar-z が次のような無限小変化をしたとき、
(Eq.32)

Eq.24 のプライマリー場は、次のように変化する。
(Eq.33)
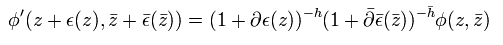
つまり、
(Eq.34)
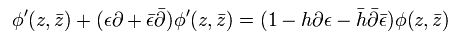
場の無限小変換を次のように定義する。
(Eq.35)
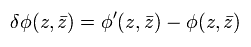
Eq.34 と Eq.35 から、 場の無限小変換は、
(Eq.36)
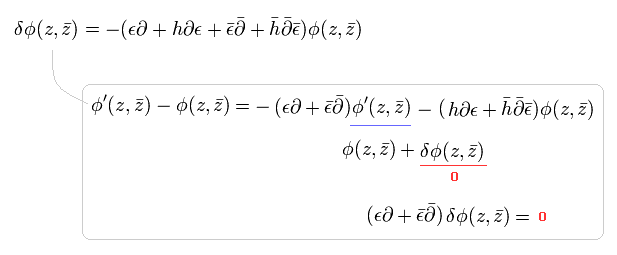
相関関数は 経路積分を用いて 次のように表せる。
(Eq.37)
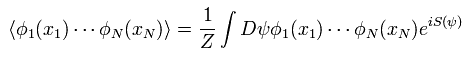
ここで ψ は 積分変数を意味する。
(Fig.2) 経路積分は "実在性の" 物理なのか ?
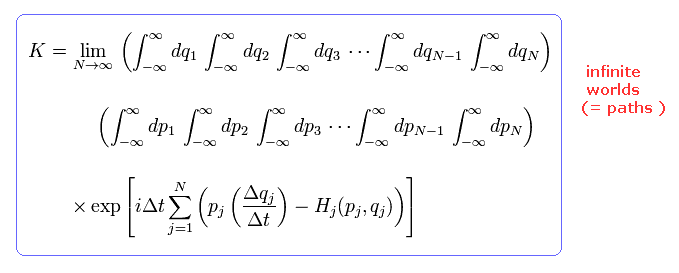
相対論的な場の量子論では、最初と最後の途中の経路にあるすべての通り道を重ね合わせなければならない。
つまり、あらゆる変数に関して 無限大から無限大の積分をしなければならない。
非常に厳しい対称性を保つためには、関数は すべての状態を含まなければならないと彼らは主張しているのである。
しかし あなた方は この多世界様の経路積分が 実在性の物理で 実際に役立つと思われるだろうか?
各積分変数は すべての種類の状態を含んでいるため、次のように書きかえることができる。
(Eq.38)
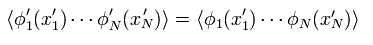
ここでは x を x' にも変更した。
Eq.24 と Eq.38 から、
(Eq.39)
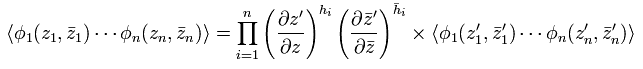
Eq.32 を使うと Eq.39 は、
(Eq.40)
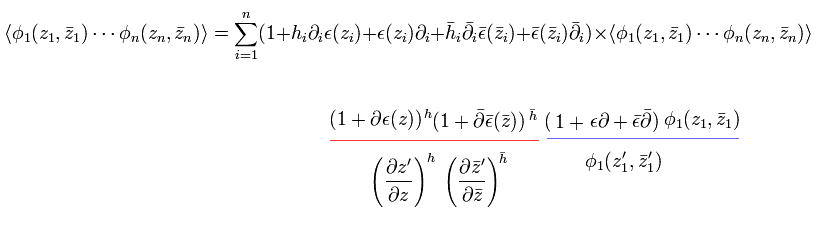
そのため、
(Eq.41)
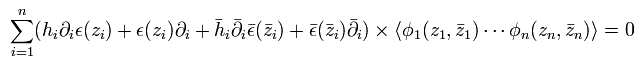
次のような無限小変化を考える。
(Eq.42)
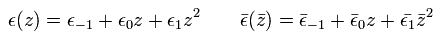
2点相関関数を次のように定義する。
(Eq.43)
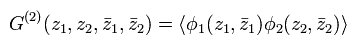
Eq.42 の無限小変換が 次の単純な並進変換のとき、
(Eq.44)
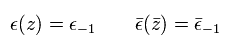
Eq.41、 Eq.43、Eq.44 から、
(Eq.45)
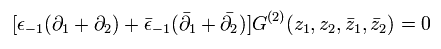
ε と bar-ε は 互いに独立である。
そのため Eq.45 が成り立つには、 相関関数は次の形になる必要がある。
(Eq.46)
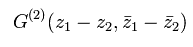
ここで
(Eq.47)
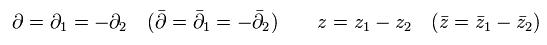
これはつまり G は (z = z1 - z2) と その bar-付きの関数になる必要がある。
次に 無限小スケール変換を考える。
(Eq.48)
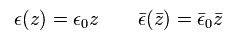
Eq.41 と Eq.48 から、 次を得る。
(Eq.49)
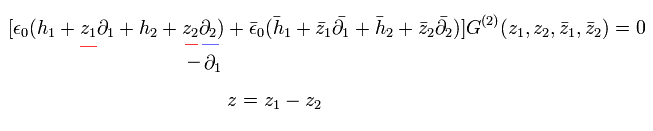
Eq.47 と Eq.49 から、 z 部分の方程式は、
(Eq.50)
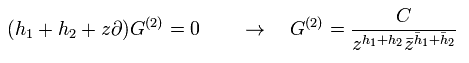
最後に 特殊共形変換について考える。
(Eq.51)
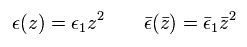
Eq.51 と Eq.41 から、
(Eq.52)
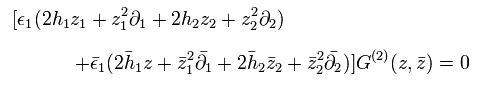
Eq.47 を使って、
(Eq.53)
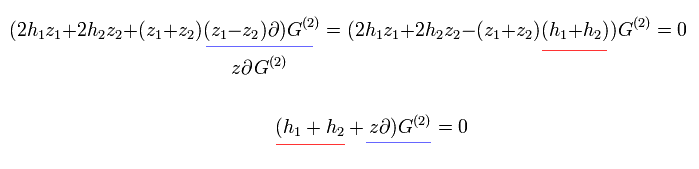
よって、次を得る。
(Eq.54)
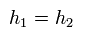
このセクションでは 自由スカラー場 (= ボソン ) の作用 について扱う。
このスカラーボソン場は 標的空間が 何と 26 次元にもなる必要がある。
まずは この 26 成分のうちの1つを扱う。
ユークリッド空間の計量 (Eq.9) での 通常のボソン場の作用 S は、
(Eq.55)
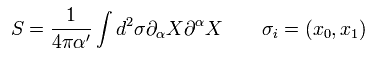
ユークリッドの計量では、添え字 α の位置 (上とか下) は重要ではない。
また、Eq.55 では、計量 g は Eq.9 に固定してある。
なぜなら、たとえ Eq.2 の共形変換を Eq.55 にしても、計量の行列式の平方根が 計量の変化を打ち消すからである。
(= このページ ( ワイル対称性 Eq.40、 Eq.47-Eq.49 ) を参照のこと。 gαβ の表記を hαβ に変えて。 )
Eq.13、 Eq.15、 Eq.18 の複素平面では、Eq.55 の作用 S は 次のようになる。
(Eq.56)
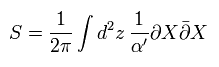
なぜなら ヤコビアンは、
(Eq.57)
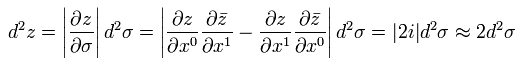
また、
(Eq.58)
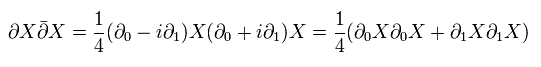
よって、 Eq.55 は Eq.56 に等しいことが分かった。
経路積分法を用いて、X 場の遷移を考える。
相関関数は次の汎関数微分で変化しない。
(Eq.59)
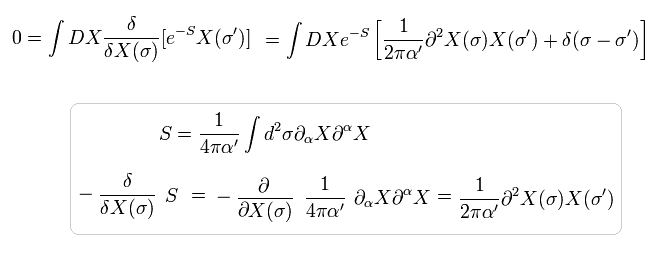
ここでは Eq.55 の作用と 部分積分を用いて 符号を変えた。
( × 2 は 微分によって生じた。 )
また 汎関数微分は 積分内部に作用するので
(Eq.60)
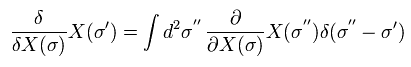
Eq.59 から、次を得る。
(Eq.61)
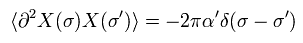
注意:このデルタ関数は2次元であり、偏微分は x0 と x1 の合計である。
(Eq.61-2)
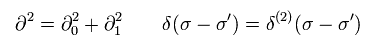
ここで 次の公式を用いる。
(Eq.62)
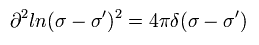
Eq.62 を証明する。
最初に σ' = 0 とする。
Eq.62 を x0 と x1 で微分する。
(Eq.63)
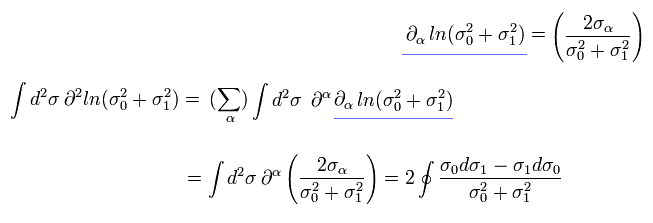
Eq.63 の 分母は (1,1) の計量でスカラーである。
Eq.63 の 分子 に 次のグリーンの公式を用いる。
(Eq.64)
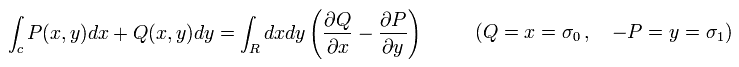
(Fig.3) 反時計回りの線積分 = c.
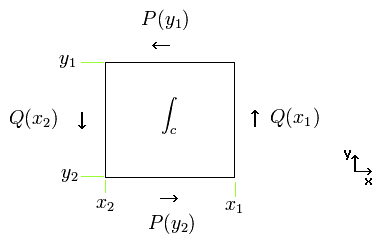
Fig.3 により、 Eq.64 の右辺は、
(Eq.65)
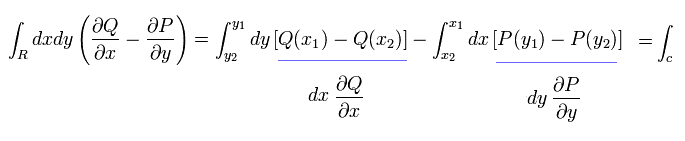
これは 反時計回りの線積分に等しい。
ここで極座標を用いる。
(Eq.66)
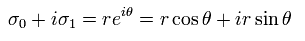
すると 次を得る。
(Eq.67)
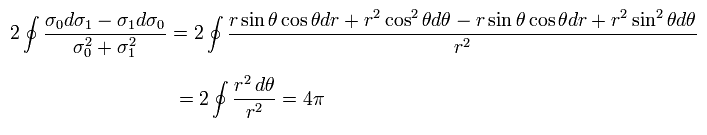
結果的に Eq.62 を証明できた。
Eq.62 を Eq.61 に代入すると、次を得る。
(Eq.68)
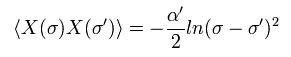
Eq.56 より、 Eq.30 のオイラー・ラグランジュ方程式は、
(Eq.69)
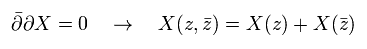
これはつまり、 X は z と bar-z の項に分離できることを意味している。
Eq.13 より、
(Eq.70)
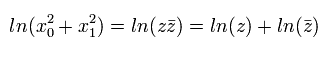
Eq.70 を用いて、Eq.68 の z の項のみピックアップする。
(Eq.71)
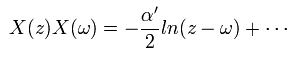
Eq.71 から、 次を得る。
(Eq.72)
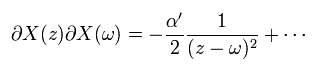
Eq.56 と Eq.31 より、 このスカラーの作用のストレスエネルギーテンソルは、
(Eq.73)
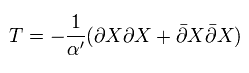
ここで -2π をかけている。
Eq.72 と Eq.73 から、T×T の 演算子積展開 (OPE) は、
(Eq.74)
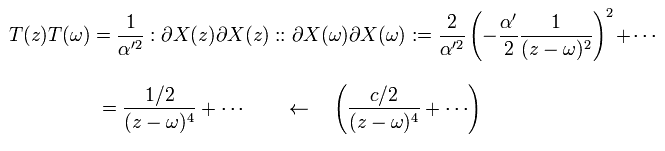
ここで : : は 正規順序積というものだが、あまり気にしなくていい。
X-X の組み合わせは 2通りあるため、Eq.74 には "2" が付加されている。
OPE は 相関関数を考えるとき重要である。
定義により、Eq.74 の "c" を セントラルチャージと呼ぶ。この意味は後で説明する。
このセントラルチャージは 臨界次元 ( ボソンでは 26 次元 ) に影響すると彼らは主張している。
Eq.74 の場合では スカラーボソンのセントラルチャージは "1" で D 次元だと 1×D となる。
しかし 残念ながら ここには リアリティーや現実と結びついたものなどは何も存在しない。
実際に計算を役に立たせるには ゲージや計量 g を何らかの値に固定しなければならない。
計量をあるゲージに固定するために 次のデルタ関数を使用する。
(Eq.75)
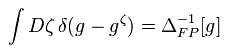
と
(Eq.76)
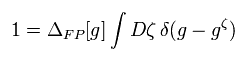
このページ (ゴーストと BRST 変換は物理 ?) で、 非常に奇妙な概念であるゴースト と グラスマン数 ( b, c ) を導入した。
(Eq.77) グラスマン数の性質。
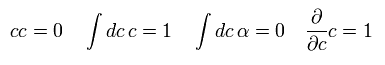
上記に示したページで、次のゴーストの作用を得た。
(Eq.78)
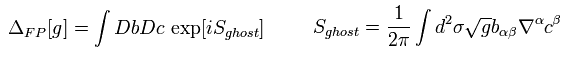
ここで bαβ∇αcβ は "スカラー" を形成している。
また ユークリッド時空間の計量 g は Eq.9 にゲージ固定で固定してある。
Eq.13、 Eq.16、 Eq.18 と Eq.57 を用いて、
(Eq.79)
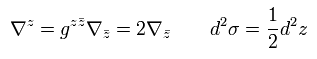
Eq.78 の作用は 次のように変化する。
(Eq.80)
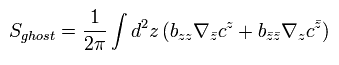
ここで "b" を 対称かつトーレース和ゼロと定義する。
(Eq.81)

よって 表記を次のように変える。
(Eq.82)
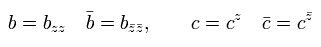
最終的に 次のゴースト作用を得た。
(Eq.83)
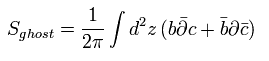
Eq.30 のオイラー・ラグランジュ方程式と、 Eq.83 より、 次の関係式を得る。
(Eq.84)
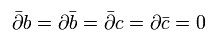
つまり b と c は z のみの関数である (= ホロモルフィック ).
また bar-b と ba-c は bar-z のみの関数である (= 反ホロモルフィック ).
Eq.59 のように、(b,c) の相関関数は 次から得られる。
(Eq.85)
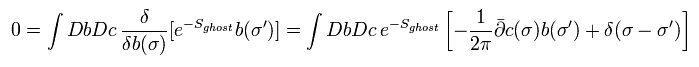
Eq.83 と Eq.85 から、 次を得る。
(Eq.86)
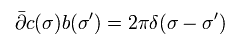
同様に、
(Eq.87)
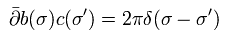
ここでは 部分積分と、反交換の性質を利用している。
Eq.83 より、 次の相関 ( b-b と c-c ) はゼロになる。
(Eq.88)
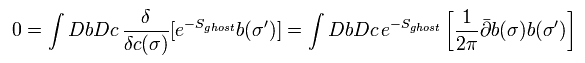
次の公式を用いる。
(Eq.89)
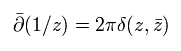
Eq.89 を bar-z に関して積分すると、
(Eq.90)
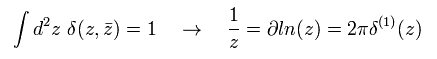
Eq.62 と Eq.70 を用いて、
(Eq.91)
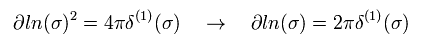
Eq.90 を得た。
Eq.86、 Eq.87、 Eq.89 から 次を得る。
(Eq.92)
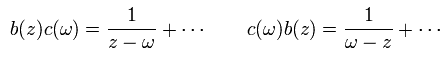
ここで Eq.43 と Eq.46 を用いた。
Eq.31 と Eq.83 を用ると、 (b,c)-ゴースト のストレスエネルギーテンソルは、
(Eq.93)
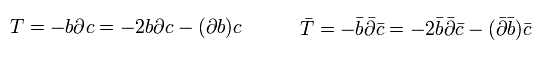
Eq.73 のように、 -2π を乗じている。
Eq.93 では、 部分積分をして b と c の両方の変分ができるようにしてある。
結果的に、Eq.93 より、ストレスエネルギーテンソルのペア (= TT ) は 次のようになる。
(Eq.94)
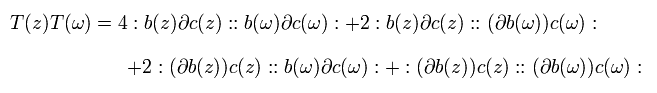
Eq.92 と 次の関係式を用いて、
(Eq.95)
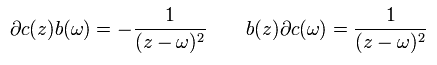
と
(Eq.96)
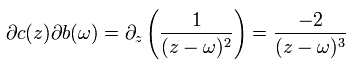
次を得る。
(Eq.97)
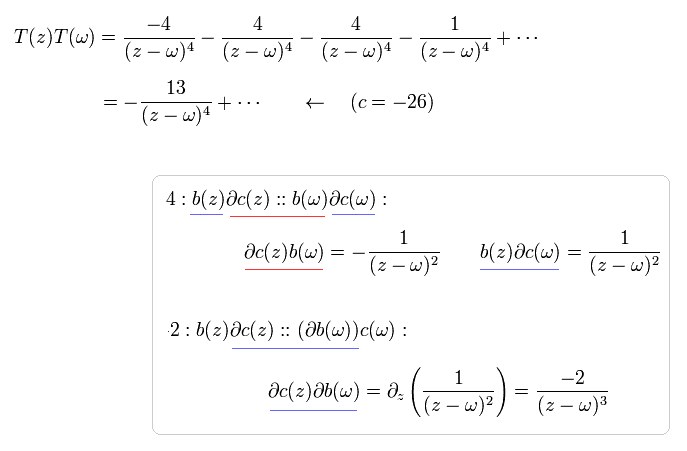
つまり、b,c-ゴーストのセントラルチャージ c は、 -26 となる。
Eq.74 に示したように、D 次元のスカラー場の セントラルチャージ は "D" である。
つまり、セントラルチャージ全体がゼロになるには D が 26 次元 にならなければならない!
(Eq.98)
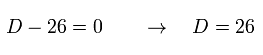
残念ながら、ここにはリアリティーのかけらもない。
(フェルミ粒子に関しても同様に新たなゴーストをこしらえて、結果 10 次元を得る。)
しかし まず最初に (b,c)- ゴーストは 単なる 数学上のゴースト である。それなのに このゴーストから "物理的" かつ "実在性" の ストレスエネルギーテンソルを得ることができるのだろうか?
後で説明するが、セントラルチャージがゼロになることは、群論における 対称性にとって重要である。
(Eq.99)
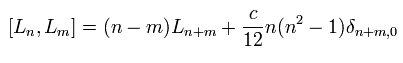
このページ ( Virasoro 代数とセントラルチャージ ) を参照するように。
Eq.99 の "c" がゼロでないと、 Eq.99 は 群論 と 対称性 にとって美しくないというわけである。
また このページ (Eq.25, 26, 27, 31, 32)に示したように、セントラルチャージの存在は 量子力学の 変換の生成子 (Q) と 無限小変換の関係を ある状況で壊してしまう。
そのため 彼らは Eq.99 のセントラルチャージがゼロにならなければならないと主張している。
そのかわり、奇妙な 26 次元 (もしくは 10 次元) を受け入れなければならないのである。
残念ながら、これらは単なる "数学" であり、リアリティーがない。
( 余剰次元と 非対称のどっちが深刻 と思われるだろうか? )
さらに、彼らは BRST 不変性や 超対称性のような 人為的な数学上の対称性を導入しようとしている。
つまり 彼らは 現実世界ではなく、単なる "数学上"の対称性のみを追及しているような感じである。

2012/8/24 updated This site is link free.