Top page ( All quantum mechanical methods including DFT are wrong )
QM/MM
(Fig.1) Quantum mechanical methods fail in actual science.

In fact, all quantum mechanical calculation methods including the most popular one-pseudo-electron density functional theory (= DFT ) are wrong and useless
In present condensed matter physics and protein interaction, they depend on density functional theory (= DFT ) as quantum mechanical method.
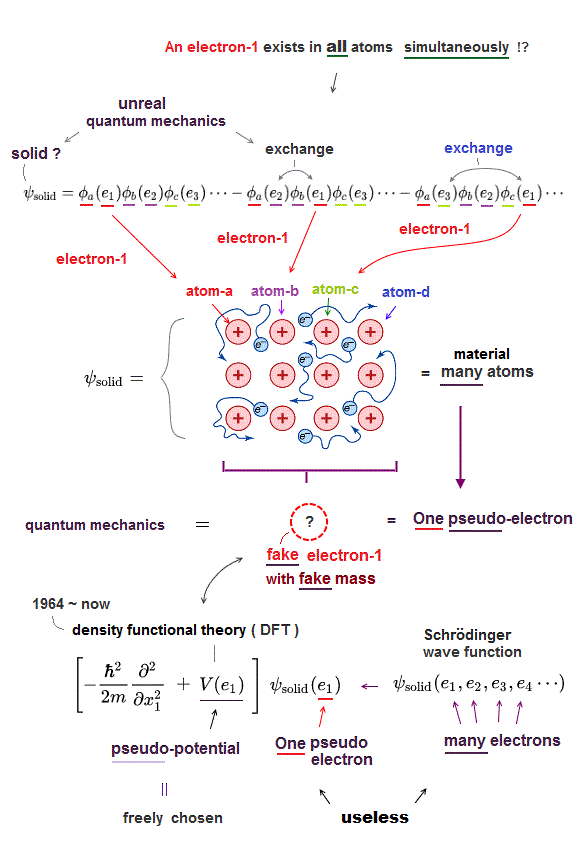
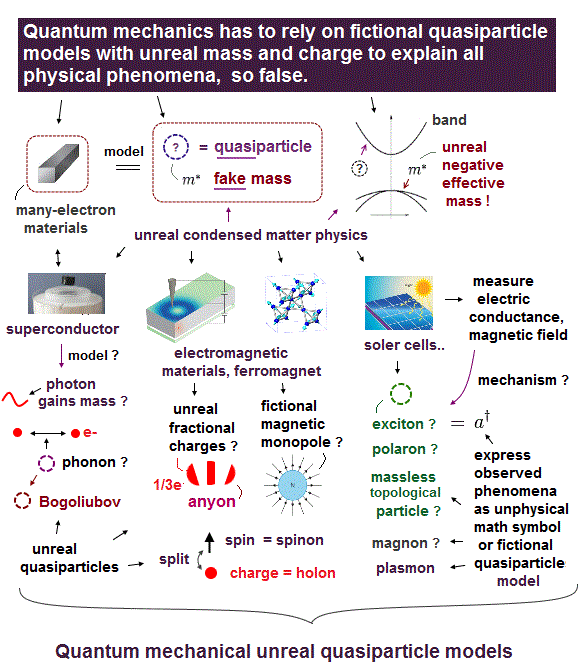
Schrodinger equation in quantum mechanics cannot handle multi-electron atoms, which is the reason the present solid physics depends on unreal quasiparticles.
So density functional theory (= DFT ) based on Schrodinger equation is useless, too.
(Fig.2) Quantum mechanics gives unreal hydrogen model with spin ↓
Bohr model first succeeded in explaining hydrogen energy levels, and was replaced by quantum mechanics in 1920s.
Quantum mechanics relies on Schrodinger equation in calculating atomic energies.
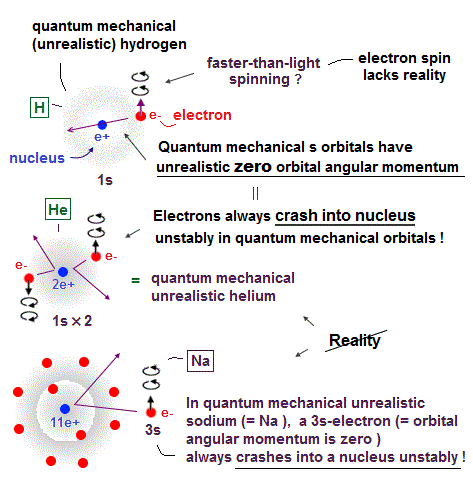
Atomic models by Schrodinger equation is very unrealistic
Surprisingly, quantum mechanics requires that s orbitals (= ground state ) have zero angular momentum ( this p.2 ). ←Electrons often hit nucleus ?
Furthermore, quantum mechanics needs nonsense spin, which spinning must far exceed light speed to generate experimental magnetism.
(Fig.3) No solution → just "choose" trial functions ! = useless
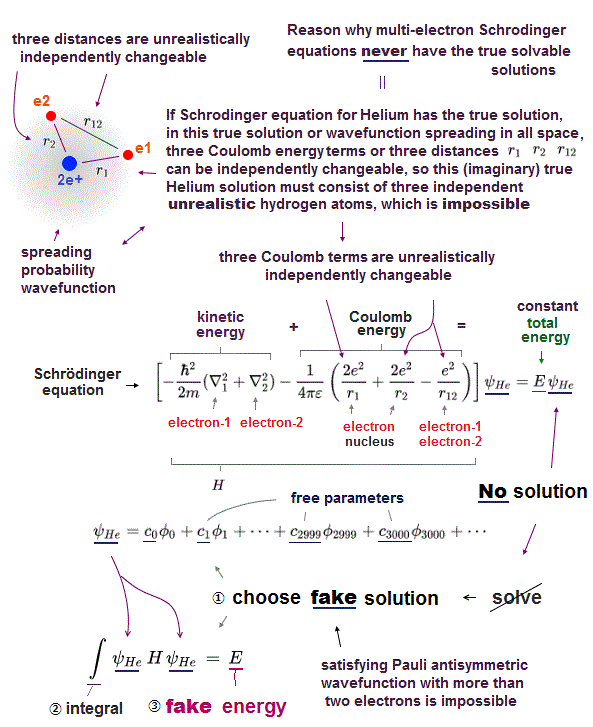
Schrodinger equation of two-electron helium contains interelectronic Coulomb energy. So it has No solution of helium.
All other multi-electron atoms including H2+ molecule ion have No exact solution. Then how does quantum mechanics deal with multi-electron atoms ?
Surprisingly, they just choose artifical trial function as "imaginary" solution.
"Choosing" convenient hypothetical solution out of infinite choices means Schrödinger equation has no ability to predict multi-electron atoms.
And it's impossible to try infinite kinds of trial wavefunctions and find the one giving the lowest energy in them.
(Fig.4) Schrodinger equation is useless → Imaginary target (= Einstein ).
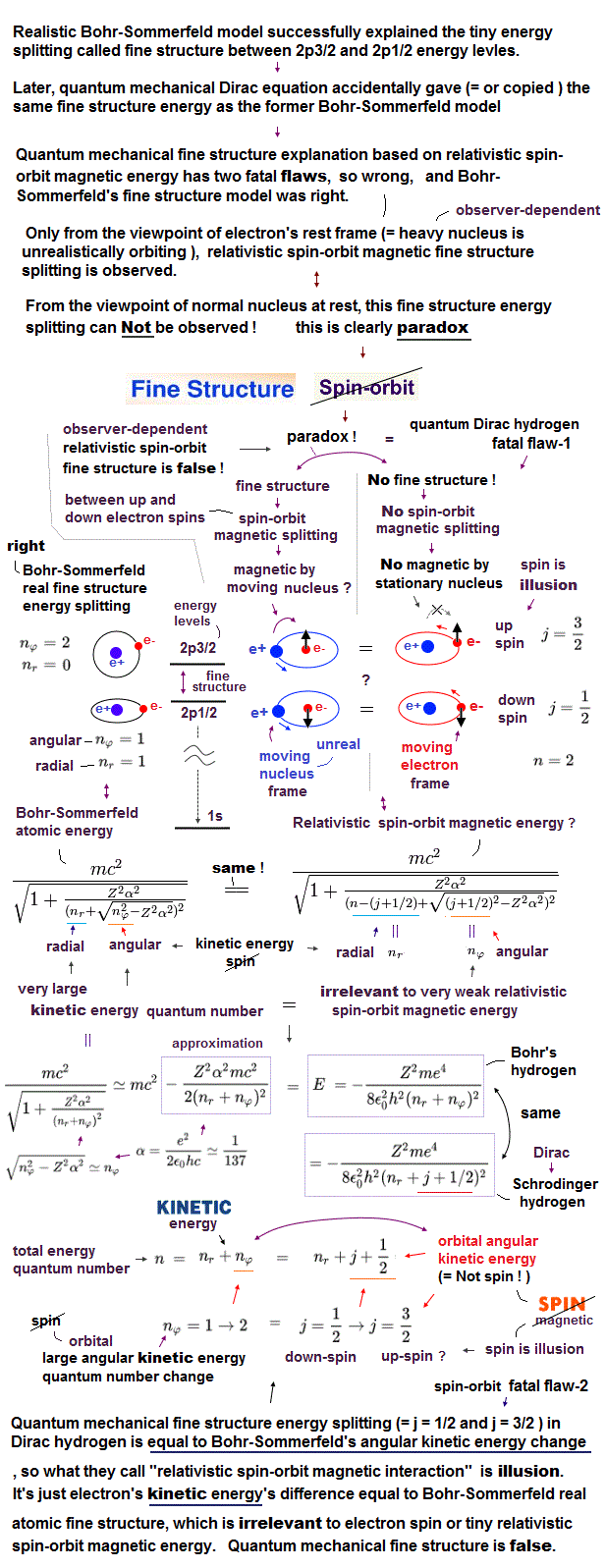
If Schrodinger equation of quantum mechanics remained useless, cannot handle multi-electron atoms, physicists has nothing to do.
This is the reason they fabricated relativistic quantum field theory as "imaginary" target, though it depends on contradictory virtual photon and paradox.
This quantum field theory is the main reason why the present Higgs and Pauli principle have to rely on abstract, nonphysical expression.
Quantum field theory uses only Einstein relativity and de Broglie relation as Dirac equation, not Schrodinger equation.
(Fig.5) Kinetic + Coulomb energies = constant total energy E.
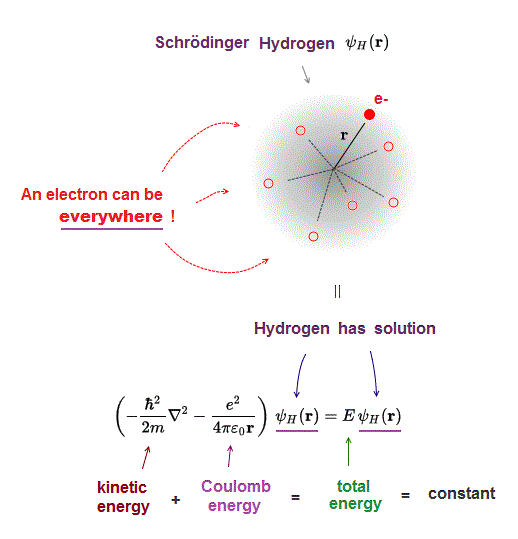
It is known that Schrodinger equation of one-electron hydrogen can be solved. Total energy E is the sum of kinetic and Coulomb energy.
Solving Schrodinger equation means we can find the common hydrogen wavefunction which gives the constant total energy E value.
(Fig.6) Schrodinger's hydrogen = de Broglie + Coulomb energy.
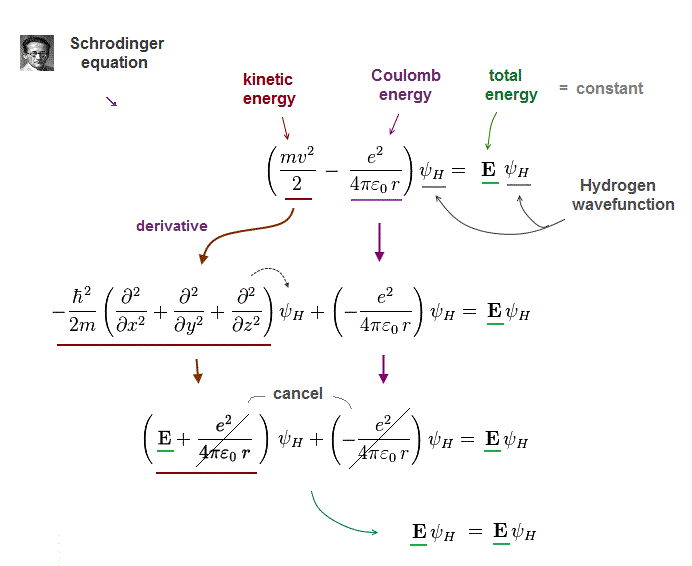
Electron's de Broglie wave was confimed in various experiments ( ex. Davisson-Germer ). So Schrodinger equation also uses this de Broglie theory.
According to de Broglie theory, electron's momentum (= mv ) is expressed as h/λ (= wavelength ).
Schrodinger equation uses this relation in kinetic energy term by acting derivative operator (= ∇ ) to wavefunction.
(Fig.7) Schrodinger's hydrogen obeys n × de Broglie wavelength.
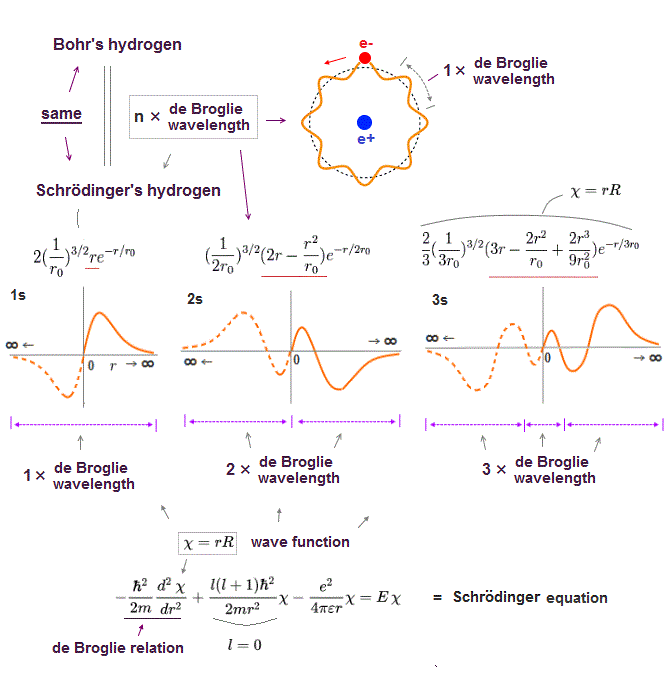
It's a famous story that old quantum orbits become an integer times de Broglie wavelength.
In fact, Schrodinger 's hydrogen wavefunction also satisfies this integral multiple of de Broglie wavelength ( this p.9 ), though they don't admit it openly.
Without this de Broglie boundary condition, hydrogen ground state energy can get lower than experimental value, unlimitedly !
The point is this de Broglie condition (= an integer times wavelength ) is valid only when Schrodinger equation can be solved exactly like in hydrogen atom.
So in all other unsolvable atoms, Schrodinger equatin disobeys not only energy conservation but also de Broglie condition ! This is the reason they are useless.
(Fig.8) Electron-electron interaction is unsolvable.
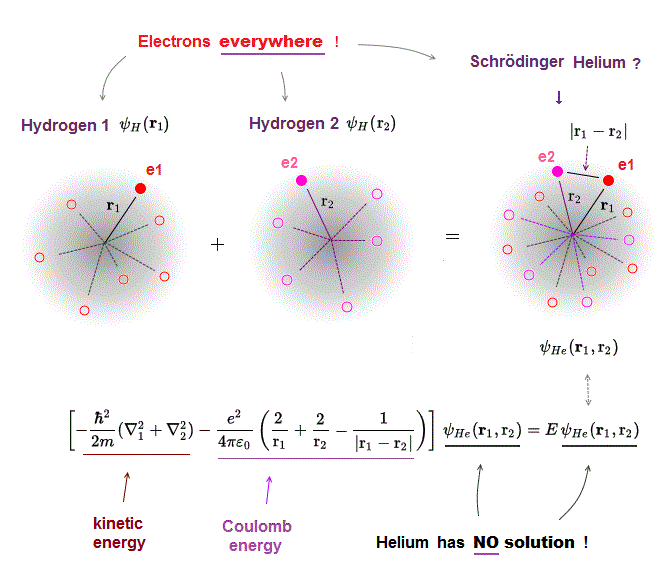
In fact, Schrodinger equation is successful only in one-electron hydrogen atom.
Multi-electron atoms such as helium have NO solutions.
"No solution" means it's impossible to find the common total energy E given by the common helium wavefunction, even in approximate solutions.
(Fig.9) ↓ Variational method of Helium is impractical.
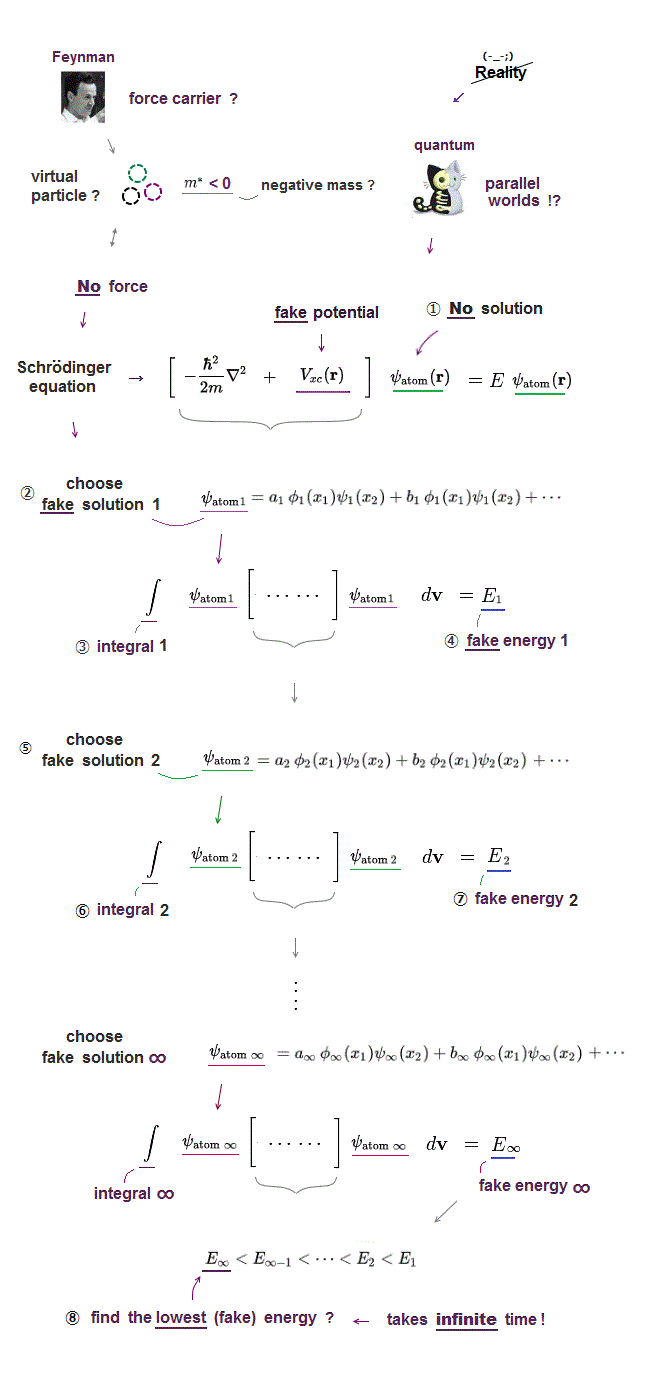
In the present useless quantum mechanics, they just guess and choose some trial function and adjust their free parameters to obtain desired energies in helium.
The problem is there are "infinite free choices" in this trial wavefunctions, so we cannot try all possibe wavefunctions to compare their energies.
It means finding the lowest ground state energy by trying infinite choices is impossible in quantum wavefunction.
All these trial function don't satisfy the total energy conservation, so "fake" energy, after all, meaningless.
The present use of "finite" basis set as approximate function never represents truth ( this p.4 )
(Fig.10) Kinetc + Coulomb (= nucleus-electron, e-e ) energy
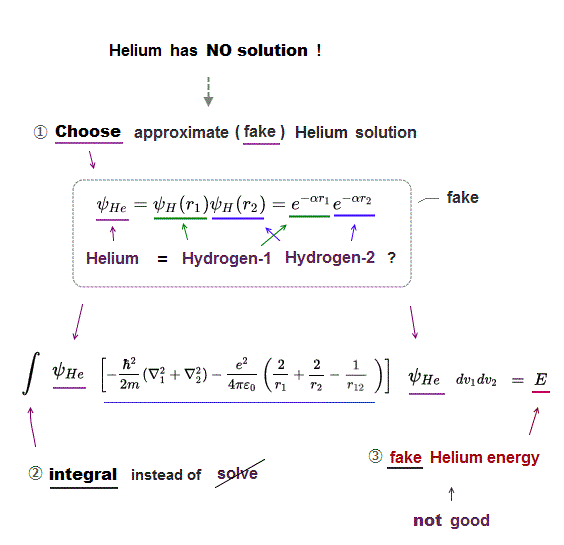
Quantum mechanics have NO exact solutions when atoms contain more than one electrons.
Schrodinger equation of multi-electron atoms consists of kinetic energy and Coulomb energy (= Ze+ nuleues - electron, electron-electron ).
All physicists can do is choose some convenient trial function out of infinite choices in unsolvable Schrodinger's atoms.
As the number of electrons increases, even this integral of approximate functions is impossible in Schrodinger equation.
(Fig.11) Density functional theory (= DFT ) uses one-eletron density (= ρ ).
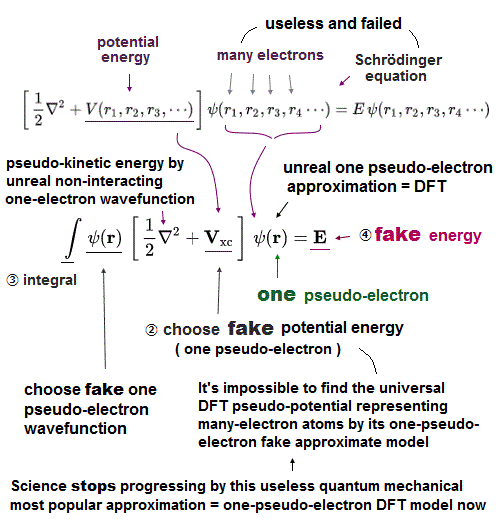
In multi-electron atoms of Schrodinger equation, even integrating (← Not solve ! ) approximate trial functions is too hard to do.
So they created new artificial method, density functional theory (= DFT ), which treats multi-electron functions as if they were "one" electron density.
Of course, there is serious side effect of this forced approximation.
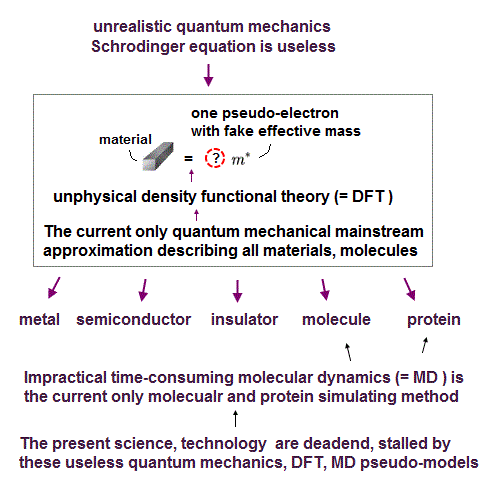
(Fig.12) Density functional theory (= DFT ) cannot handle multi-electrons.

Density functional theory (= DFT ) has serious defects.
Equations of electron-electron Coulomb energies are unknown in DFT !
DFT includes exchange-correlation enegies expressing interelectronic repulsions and Pauli principle. But DFT depends on "one-electron" density (= ρ ) approximation.
So DFT has NO ability to handle multi-electrons from the beginning.
( Of course, Schrodinger equation itself cannot handle multi-electrons ).
In density functional theory (= DFT ), the "form" of Coulomb repulsions are NOT specified, so physically meaningless and useless.
Exchange-correlation term is unknown in DFT, see this p.2 and this p.8
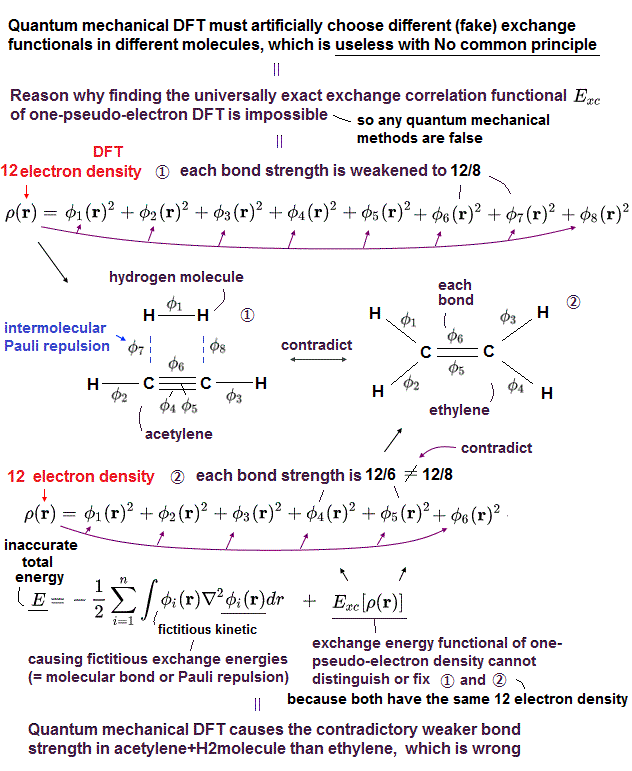
(Fig.13) Unknown exchange-correlation energy can be freely determined !
Density functional theory (= DFT ) does NOT have the standard "form" of interelectronic Coulomb energy and Pauli principle from the beginning.
So in DFT, physicists have to choose and determine "convenient form" of interelectronic repulsions out of infinite choices !
Artificially choosing convenient forms means DFT has NO ability to predict any physical values like ordinary Schrodinger equation !
No functional (so far) is accurate for all properties of interest. No matter what functional is ‘invented’ someone will always find a case where it fails ( this p.17 ).So DFT is one of empirical methods, NOT first-principle at all ( this p.23 )
(Fig.14) Fatal cancer, HIV, ALS, dementia remain incurable.
If basic quantum mechanics remains useless and unrealistic, all other applied fields such as solid-physics and biology remain useless, too.
This is a serious problem, because it's impossible to cure fatal diseases such as cancer, HIV, ALS.. forever, as long as we believe fictional physics !
(Fig.15) Unreal many-worlds, quasiparticle, computer .. → exorbitant tuition !
If basic physics such as quantum mechanics and Einstein relativity remain useless and unrealistic, who benefit from it ?
The center of fraudulent science is for-profit universities and academic journals, which try to protect their vested interests.
As a result, students all over the world are suffering from exorbital tuition and skill mismatch.
Academic organizations originally have to contribute to the scientific advance, but conversely, they take the lead in preventing us from developing science !
Fictional quantum computer is just a "scam" to defraud people and corporations of their money. Actually, it remains useless ( forever ) except in media-hype.

2016/4/29 updated. Feel free to link to this site.