Top page ( correct Bohr model )
All atoms through de Broglie waves
Realistic atomic Neon structure
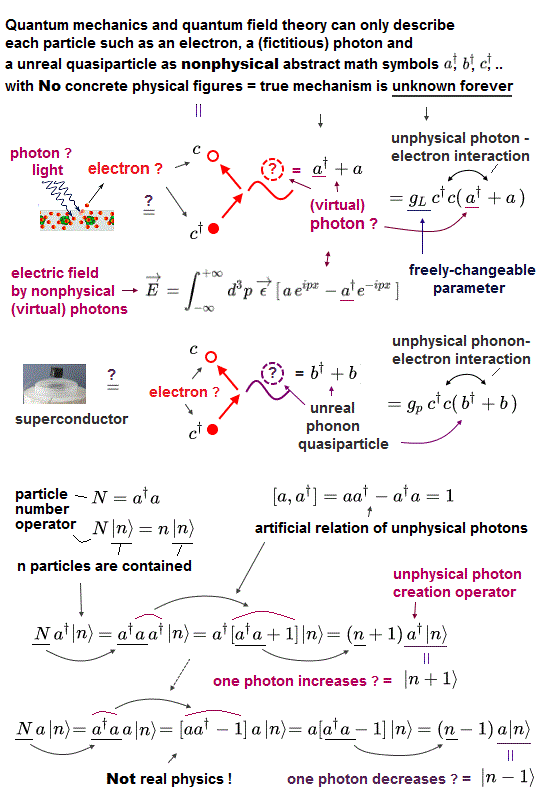
(Fig.1) "Photon" is just abstract math symbol (= a† ), without physical shape.

Quantum mechanics claims that the classical Coulomb force is caused by photon exchange.
But clear mechanisms of "attractive" and "repulsive" Coulomb forces remain unknown.
In fact, this photon causing Coulomb force is virtual photon, so NOT real ( see this, this, this ).
Surprisingly, this virtual photon is superluminal tachyon, violating Einstein's relativity ( see this, this ).
By the way, what is the physical shape and size of a single photon ?
Unfortunately, quantum mechanics cannot answer this basic question.
In QED, these photons must be described using abstract Feynman diagram.
This Feynman QED has NO ability to show photon's clear picture at all.
All quantum mechanics can show is meaningless math symbols ( see this, this p.3 ).
It contains only rough actions, "a photon is created (= a† )", or "annihilated (= a )". That's all, NOT physics.
(Fig.2) Light frequency (= f ) equal to c/λ (= light wavelength ) proves "Wave" !
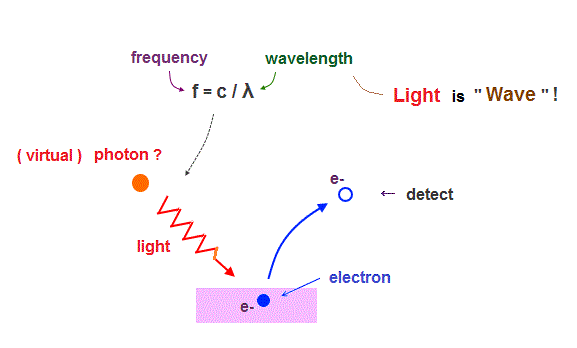
Though almost all textbooks say photoelectric effect proposed by Einstein proved particle nature of "photon", this far-fetched interpretation is clearly "brainwashing" by textbooks.
Electrons are "emitted" from metals, when illuminated by light of higher frequency than some threshold, irrelevant to its intensity. So they ( this, this, this ) affirmed that light is "particle".
But as you know, light frequency (= f ) is equal to c/λ (= wavelength ). See this site.
"Frequency" and "wavelength" clearly mean "wave" ( NOT particle ! ) nature of light.
So, the idea "photoelectric effect = light frequency = photon " is one of mind-controls by textbooks and media, like Bohr's accelerating electron ( though it does NOT lose energy ).
In fact, Lamb (= Nobel winner ) argued that the photoelectric effect happens without photon.
Imaginary "photon" is necessary for quantum field theory such as Higgs and string theory.
But these photon's operators (= a†, this, this p.5 ) are just abstract math symbols with NO realistic shapes.
(Fig.3) The wavelength of radio wave (= one of lights = photon ? ) is 1000 meter !
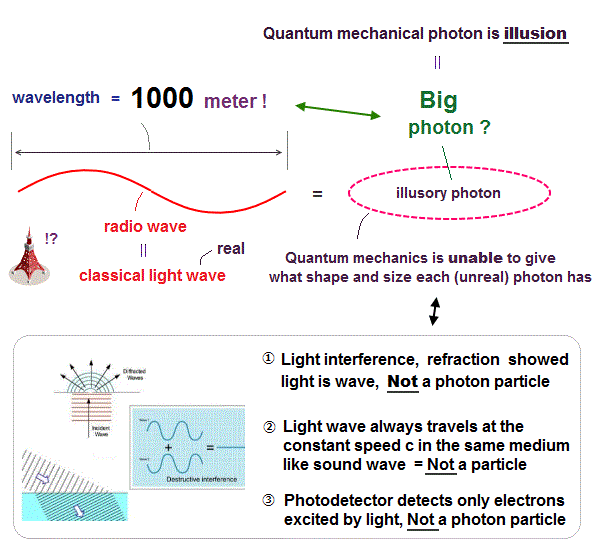
About the unphysical photon, see this page.
(Fig.4) Davisson-Germer experiment showed an electron is de Broglie wave.
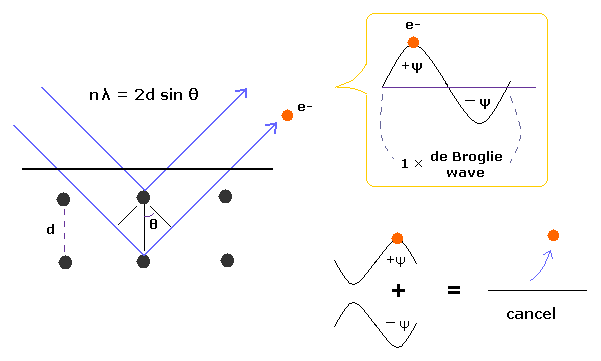
In Davisson-Germer experiment, they accelerated electrons by electric fields and made them reflected by nickel crystal.
de Broglie wavelength of an electron is gotten from the electric field strength and interference pattern of a single electron.
Experimental results agreed with de Broglie relation.
So de Broglie waves themselves are realistic concepts, though quantum mechanics avoids commenting it.
This experiment showed an single electron has wave-like property, in which the opposite wave phases cancel each other, and expel the electron.
(Fig.5) One de Broglie wavelength of electron.
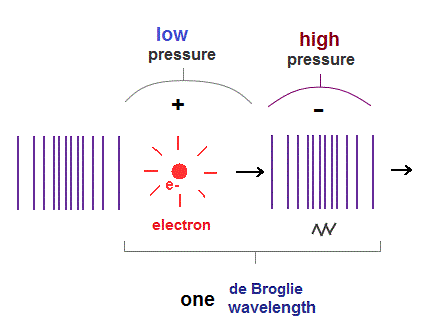
When an electron moves, electric fields (= E ) around the electron also moves with it.
So this spreading electric field causes de Broglie waves, which can be confirmed by Davisson-Germer experiment.
We can naturally think this de Broglie wave is a kind of longitudinal waves through some medium.
If so, double slit interference can be explained by this "real" de Broglie waves, NOT by "fantasy" many-worlds.
Longitudinal wave consists of "low" (= sparse ) and "high" (= dense ) pressure areas.
It is thought that an electron pushes the field around it toward "dense" area, and is moving with "low" pressure area.
About the electron interacting with light, see this page.
(Fig.35) de Broglie relation.
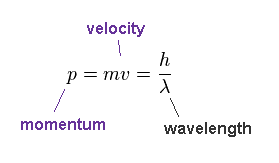
According to de Broglie relation, the momentum ( p = mv ) is expressed as ( p = h/λ ).
Here, p = momentum, m = mass, v = velocity, h = Planck constant, λ = wavelength.
As shown on this site, total energy (= E ) of electromagnetic wave is linearly proportional to frequency (= f ) through the relation of E = hf, which is confirmed in photoelectric effects.
Surprisingly, in any other particles such as electrons and protons, their frequency is proportional to their total energy, if de Broglie relation is satisfied ! Here we explain it.
(Fig.36) Electron is slower ( v → 1/2 v ), its wavelength becomes longer ( λ → 2λ ).
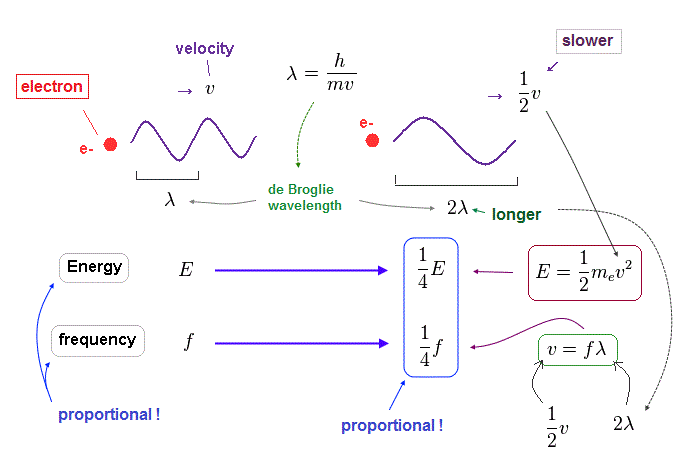
When an electron's velocty (= v ) becomes half (= 1/2 ), its total ( kinetic ) energy (= E ) becomes 1/4 of the original value, because E is proportional to a square of velocity ( E = 1/2 mv2 ).
According to de Broglie relation ( mv = h/λ ), the electron's wavelength becomes twice ( λ → 2λ ), when the velocity becomes half.
Considering wave relation ( v = fλ ), the electron's frequency (= f ) becomes 1/4 of the original value in this case.
As you see, also in electron's de Broglie wave, the energy is proportional to frequency ( E/f = constant ) !
(Fig.37) Momentum ( p = h/λ ) is constant.
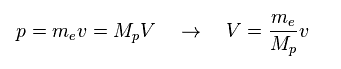
Here we think about the case when the momentum (= p ) is common in both of "light" electron and "heavy" proton.
So through de Broglie relation ( λ = h/p ), their wavelengths (= λ ) are the same, too.
Due to heavier mass ( Mp ) of proton, the velocity (= V ) of proton becomes much lower than that (= v ) of electron.
So the total kinetic energy ( E = 1/2 MpV2 ) of proton is much smaller than electron (= 1/2 mv2 ).
(Fig.38) Energy (= E ) is proportional to frequency (= f ) in electron and proton.
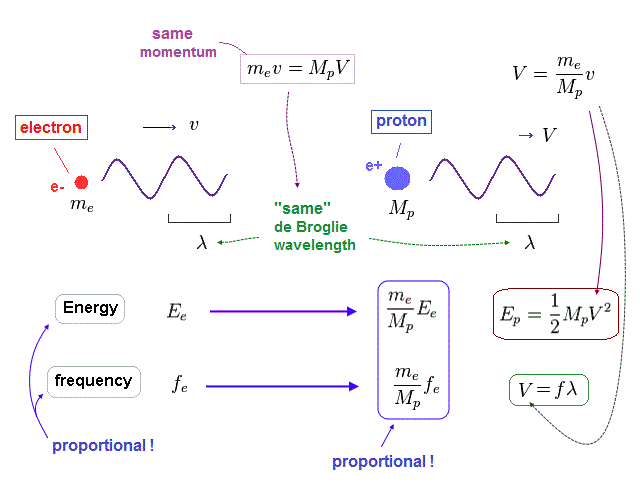
Again, through the wave relation of v = fλ, we can find the proton's frequency.
As shown in Fig.38, between proton and electron, the relation of energy (= E ) proportional to frequency (= f ) holds true.
So not only in electromagnetic wave but also in electrons and protons, the frequency has an important meaning to determine their total energy.
(Fig.39) Total energy in electron and proton.
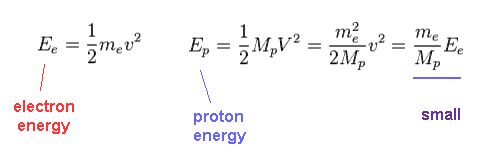
Using Fig.37, we find the proton's kinetic energy is much smaller than electron due to its large mass, even when their momentums are the same.
(Fig.40) Ratio of electron's to proton's masses.
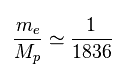
Proton (= Mp ) is much heavier ( 1836 × ) than electron's mass (= me ).
(Fig.41) Frequency = velocity / wavelength.
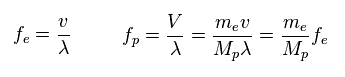
Through wave relation, we find the proton's frequency becomes much smaller than electron.
( Here the wavelengths ( momentums ) of electron and proton are the same. )
(Fig.42) Light's energy is proportional to its frequency, too.
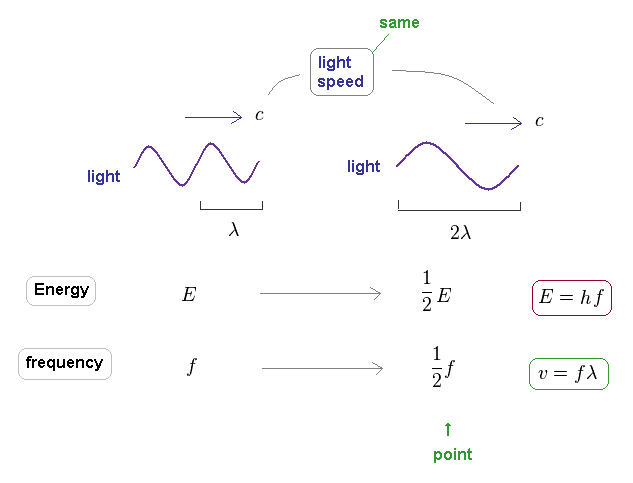
It is known that light's energy is also proportional to its frequency through the relation of E = hf.
The important point is that the speed of the light is always constant "c", different from other particles.
This means there is NO concept such as "acceleration" in light ( and neutrino ).
When electron's ( or proton's ) wavelength changes, both of its velocity and momentum changes.
So the electron's frequency is inversely proportional to a square of wavelength, as shown in Fig.36.
On the other hand, due to neglecting light speed change, the light frequency is just inversely proportional to its wavelength.
As you see, de Broglie wavelength ( λ = h/p ) expresses "contraction" ( or expansion ) of the field by the momentum (= impulse ), compared to its equilibrium state, irrelevant to the velocities of various particles.
(Fig.43)
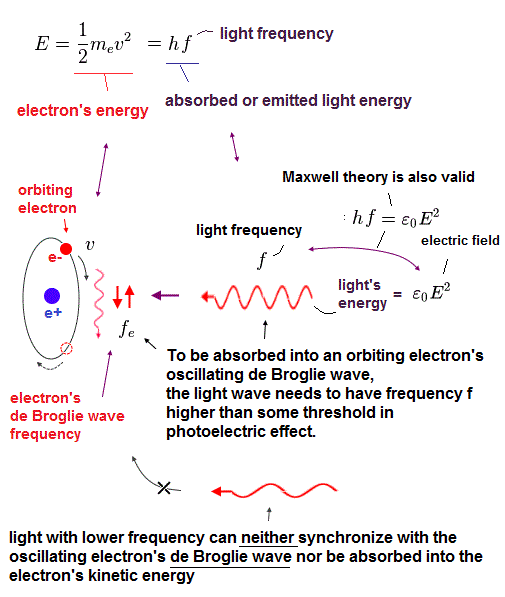
Here we investigate the relation between electron's frequency (= fe ) and emitted light's frequency (= f ).
In Fig.43, total kinetic energy of electron (= 1/2mv2 ) is equal to light's energy (= hf ) emitted from the electron.
(Fig.44)
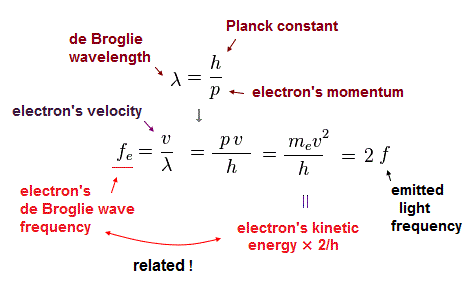
Using wave relation ( v = fλ ) and de Broglie relation ( λ=h/p ), we find that the electron's ( de Broglie ) frequency (= fe ) is two times bigger than the emitted light frequency (= f ).
(Fig.45) Oscillating electron emits light and gradually loses its energy.
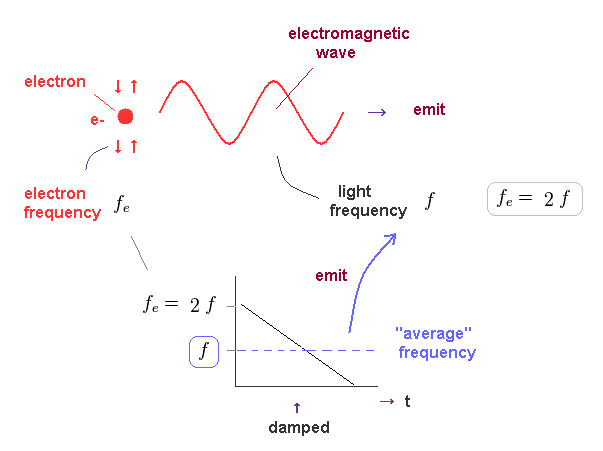
In Fig.45, we think about the case in which oscillating electron gradually emits light and loses its kinetic energy.
The initial electron's frequency is equivalent to 2 × f (= emitted light frequency ), as shown in Fig.44.
The more light the electron emits, it loses more energy, and its oscillation becomes slower ( to be zero ).
It means the average electron's frequency becomes half of the original value (= 1/2 × fe = f ) .
As a result, we can prove there is an important relation between electron's and emitted light frequencies. Planck constant (= h ) connects light and electron.
(Fig.46) Transition from excited ( n = 2, f=4 ) state to ground state ( n =1, f = 2 ).
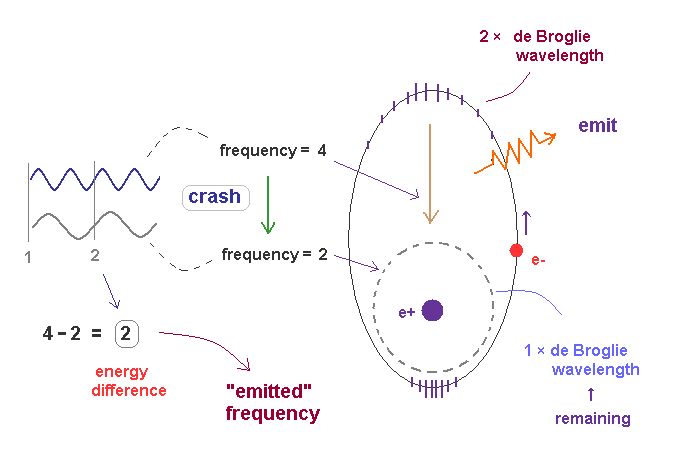
In Fig.46, the excited state of 2 × de Broglie wavelength returns to ground state (= 1 × de Broglie wavelength ).
Accelerated by Coulomb force, the final frequency of de Broglie wave of excited electron becomes f = 4.
We can think the afterimage of stable ground state de Broglie wave remains during excitation, and it is supposed to be f = 2.
These two de Broglie frequencies before and after transition are different, so they don't fit each other.
The crash between these two de Broglie waves causes swell with the frequency ( 4-2 = 2 ), which is the difference between two states.
The excited de Broglie wave is attenuated, while it emits light.
So the average frequency of emitted light becomes half of 2 (= 1 ), as is explained in Fig.45.
(Fig.47) Transition from excited ( n = 2, f=2 ) state to ground state ( n =1, f = 4 ).
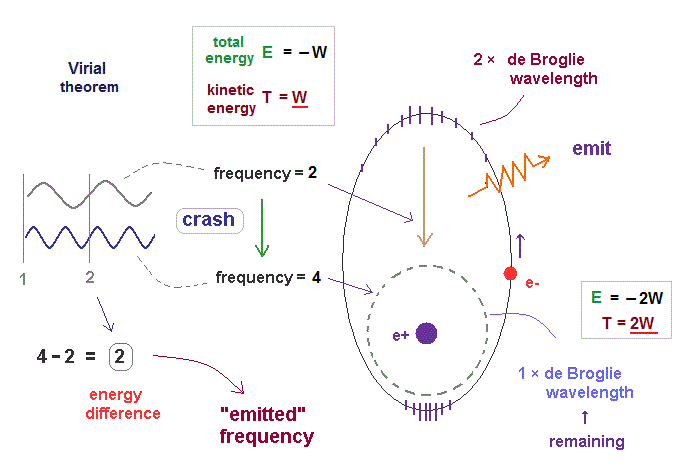
In fact, according to Virial theorem, kinetic energy T is the absolute value of total energy E ( T = |E| ).
As I said in Fig.36, electron's frequency (= f ) is proportional to its kinetic energy.
So the electron frequency in the upper energy level is lower than the lower level, like their kinetic energies. Also in this case, the frequency difference becomes 4 - 2 = 2, like Fig.46.
So the difference in total energies is just equal to the difference in kinetic energies (= frequency ) in these bound state orbits, which can explain photoelectric effect correctly in the realistic way. See this.

2015/5/17 updated. Feel free to link to this site.