Top page ( correct Bohr model )
Strange "spin" is NOT real.
How does Science make progress ?
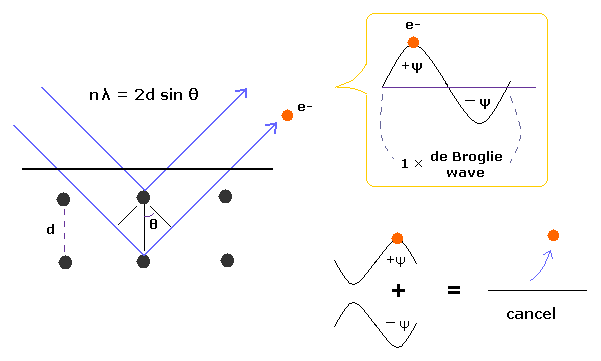
(Fig.1) Davisson-Germer experiment showed an electron is de Broglie wave.

In Davisson-Germer experiment, they accelerated electrons by electric fields and made them reflected by nickel crystal.
de Broglie wavelength of an electron is gotten from the electric field strength and interference pattern of a single electron.
Experimental results agreed with de Broglie relation.
This experiment showed an single electron has wave-like property, in which the opposite wave phases ( ±ψ ) cancel each other, and expel the electron (Fig.1).
(Fig.2) de Broglie wave ends fit.
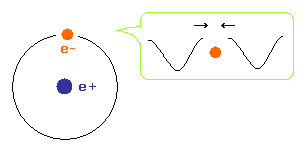
To avoid cancelling de Broglie wave, both ends of an electron wave in hydrogen atom need to agree with each other with respect to wave phases.
(Fig.3) Old Bohr's helium. Two de Broglie waves cancel each other.
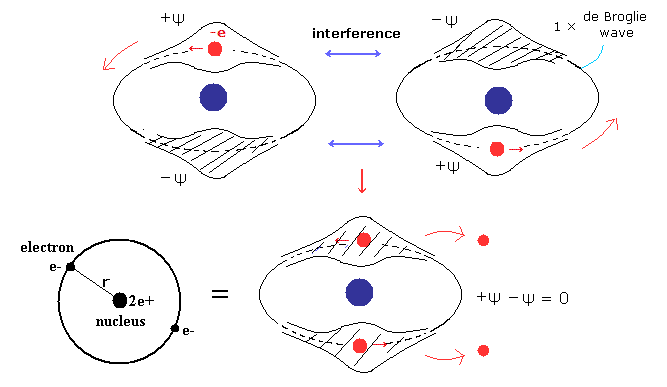
In old Bohr's helium (Fig.3), two electrons are moving on the opposite sides of the nucleus in the same circular orbit (= one de Broglie wavelength ).
Considering Fig.1 and Fig.2, two electrons of old Bohr's helium are clearly unstable due to de Broglie wave destructive interference. ( Opposite wave phases exist on the other sides in 1 × wavelength orbit.)
Actually, old Bohr's helium of Fig.3 gives wrong ground state energy of helium.
( Fig.3 gives -83.33 eV. The experimental ground state energy of helium is -79.005 eV. )
(Fig.4) Two perpendicular orbits avoid destructive interference.
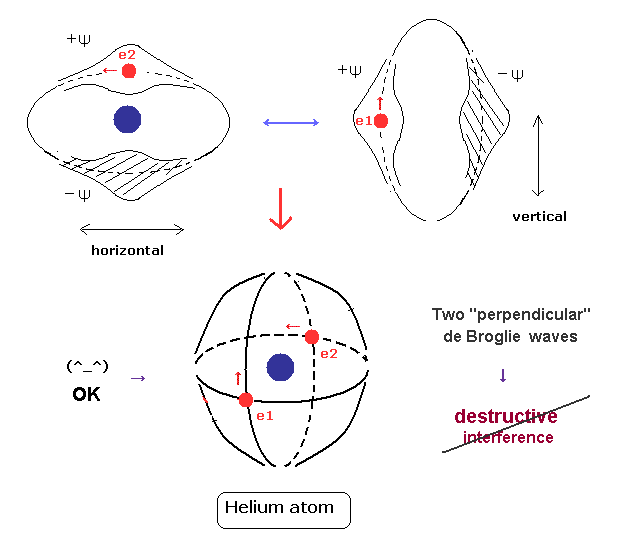
For the stability of de Broglie wave phases, destructive interference between opposite phases has to be prevented.
If two de Broglie waves of the helium electrons cross each other perpendicularly, their wave phases are independent from each other.
As a result, their destructive interference can be avoided, and 1 × wavelength orbits can be stable.
Actually this new Bohr's helium model can give correct ground state energy and Pauli exclusion principle, as shown on this page.
(Fig.5) Electron's momentum ( p = mv ) and de Broglie wavelength (= λ ).
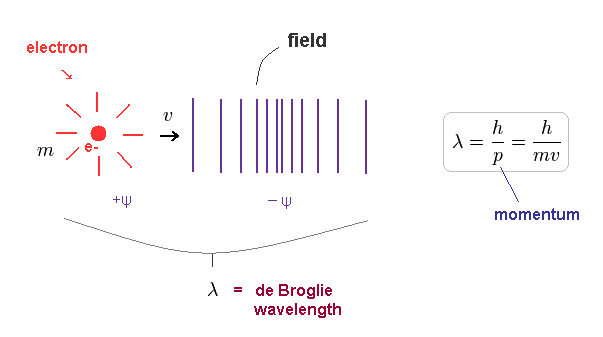
According to de Broglie relation, electron's wavelength is given by h/mv, where h is Planck constant (= h ) and mv is electron's momentum. ( "m" is electron's mass, "v" is its velocity. )
As shown on this site, the momentum is equal to the impulse (= force × time ).
So moving electrons with momentum exert forces on surrounding fields, which causes de Broglie waves.
Of course, we have to reject special relativity ( see fatal paradoxes ) to consider surrounding fields as "real" substance (= ether ).
(Fig.6) Relation among velocity (= v ), momentum (= mv ) and wavelength (= λ ).
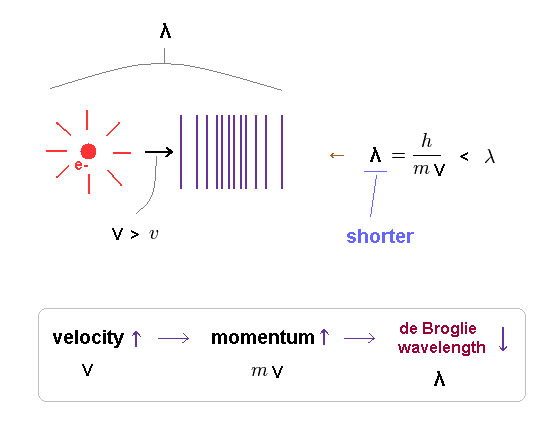
As the electron's velocity is higher, its momentum becomes bigger, and de Broglie wavelength becomes shorter.
Because greater momentum means its forces on surrounding fields gets stronger.
So we can say some classical mechanical system is working under this de Broglie relations.
Basically, each electron is accompanied by its electric field, which can generate wide-spread de Broglie wave.
Recall that electromagnetic waves consisting only of electric ( magnetic ) fields is one of de Broglie waves.
(Fig.7) 1 × de Broglie wavelength consists of a pair of opposite phases (= ±ψ ).
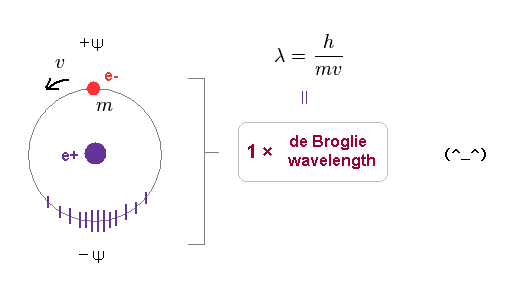
As shown on this page, we have proved that both Bohr model and Schrodinger's hydrogen satisfy an integral multiple of de Broglie wavelength.
1 × de Broglie wavelength consists of a pair of opposite phases.
( Here, +ψ is on electron's side, and -ψ is its opposite side. ).
According to de Broglie relation, its surrounding field feels electron's momentum of "mv" as a pressure, and contracts depending on its force.
(Fig.8) When another electron enters the same orbit, the total momentum changes to "2mv".
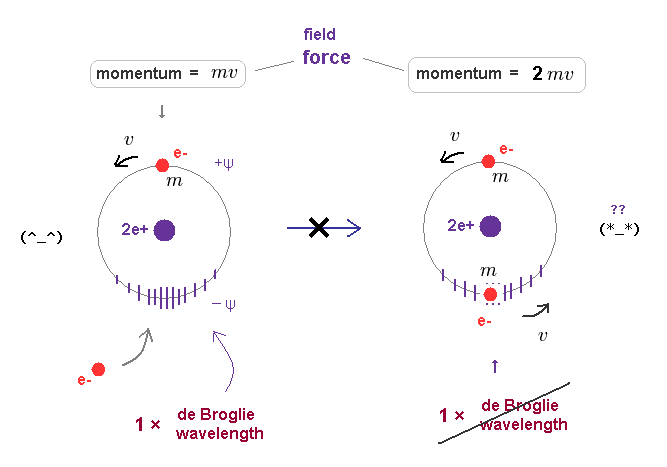
First, we consider old Bohr's helium model, in which two electrons are moving in the same orbit on opposite sides of nucleus.
Fig.8 left is helium ion (= He+ ), which orbit contracts (= -ψ ) under the pressure of one electron's momentum (= mv ). Its stable orbital length must be just 1 × λ (= h/mv ).
When another electron enters this same orbit, the pressure acting on surrounding field becomes twice ( mv → 2mv ).
Because this orbit includes total momentum of "2mv", if its orbital radius doesn't change.
If the pressure acting on the field becomes twice, the field becomes more contracted, changing Broglie wavelength.
As a result, the original relation ( orbital length = 1 × de Broglie wavelength ) cannot be kept in Fig.8 right.
(Fig.9) Total momentum becomes twice → their wavelengths become "half".
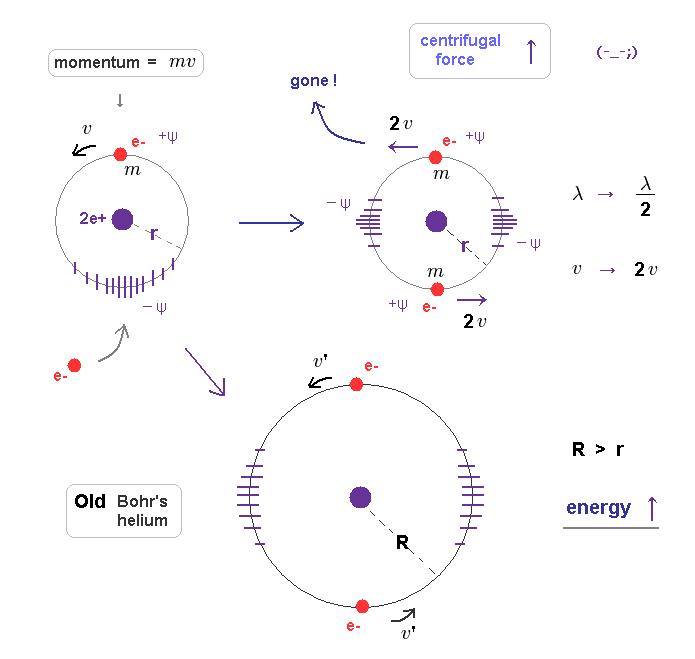
When their total momentum becomes twice ( mv → 2mv ), which causes more field contraction.
If we suppose its radius remains the same "r", each electron's velocity becomes twice to keep this field's contraction.
Coulomb attractive force doesn't change, so the higher velocity means their centrifugal forces overcome Coulomb attraction.
As a result, electrons are flying away somewhere.
If centrifugal force is equal to Coulomb force, the orbital radius has to be much longer (= Fig.9 lower ), because the next allowed orbital length is 2 × de Broglie wavelength. ( Radius is proportional to a square of "n". )
So when each orbit (= 1 × de Broglie wavelength ) contains only one electron, total atomic energy becomes the lowest and most stable.
(Fig.10) Old Bohr's helium = electrons are expelled. New Bohr helium = stable.
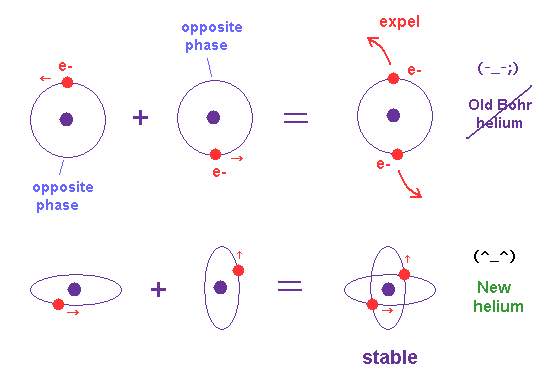
As shown in new Bohr's helium (= Fig.10 lower ), when two electrons' orbits are perpendicular to each other, their momentums are independent from each other.
So, each field feels only one electron's momentum (= pressure ) and can cause 1 × de Broglie wave stably.
This is a clear mechanism of correct helium and "real" de Broglie waves.
On the other hand, in old Bohr's helium model (= Fig.10 upper ), the forces which act on the surrounding fields becomes twice, and they cannot keep 1 × de Broglie wavelength, which expels electrons from the lowest-energy orbit.
(Fig.11) Photon is emitted from electron → its acceleration becomes "infinite" due to the sudden change.
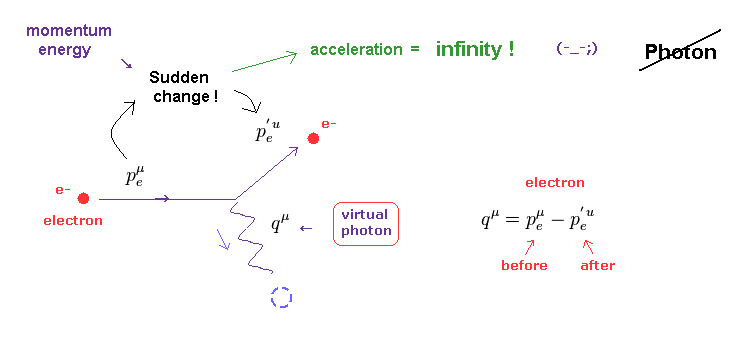
As shown on this page, a photon is just an abstract math operator with NO physical entity ( ex. size and shape ). Basically, according to the quantum field theory, the behavior of photon must be described using Feynman diagram.
Surprisingly, if the emitted ( or absorbed ) photon and electron satisfy the basic law of energy and momentum conservation, this photon always becomes virtual photon.
As shown on this page and this site, this virtual photon violates special relativity like "tachyon". This is the reason why it is called "virtual".
Furthermore, when a photon is emitted from ( or absorbed into ) an electron, this electron's momentum and energy suddenly changes.
This means the acceleration of electron at this time becomes infinity ! Impossible.
We have to consider more realistic view about lights emitted from electrons, using the whole field change and de Broglie waves, to avoid this contradiction.
(Fig.12) When electron's energy level changes from "2" to "1" quantum number, ..
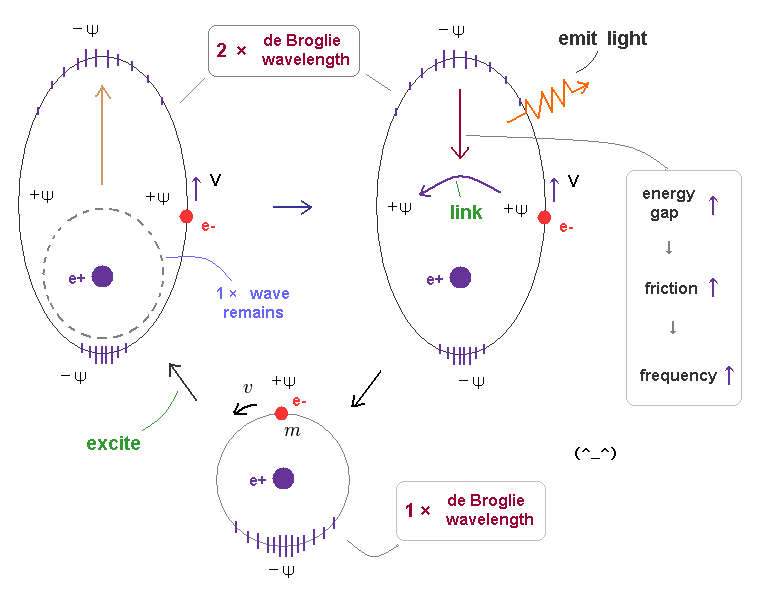
In Fig,12, the 1 × de Broglie wavelength orbit ( n = 1 ) is ground state.
This electron is excited to 2 × wavelength orbit ( n = 2 ) by absorbing light.
Excited state is transient, so the original de Broglie wave (= 1 × wavelength ) oscillation is thought to remain in this field, which may act as things for judging starting to radiate or not.
When the orbit is NOT an integer times de Broglie wavelength, it causes disharmony (= crashes between electron's waves ) inside the oscillating waves, and starts to push out (= radiate ) electromagnetic waves.
These signals ( harmony or disharmony ) are transmitted immediately (= c ) all over the orbit, which decides whether it continues radiating or stops (= untill an integer × wavelength ) in a moment during emitting light.
The potential energy can be incorporated into kinetic energy (= de Broglie wavelength ), after the electron is accelerated by Coulomb force.
Depending on the energy (= frequency ) difference between two ( initial and last ) de Broglie waves, the mean frequency (= energy ) of emitted electromagnetic waves is determined.
As their energy gap between the initial and last configurations is larger, the electron feels ( and gives ) more resistance from friction with surrounding fields (= generating light ), which makes the emitted light ( wavelength ) shorter and sharper.
(Fig.13) Electromagnetic waves are emitted in both directions.
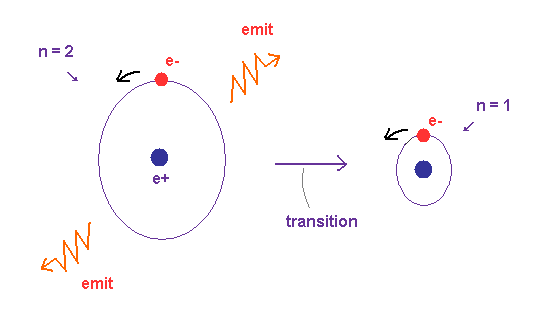
In this realistic transition model, the electron is gradually accelerated when it emits electromagnetic waves.
So the acceleration does NOT become infinite, different from Fig.11 (= quantum mechanical model ).
And of course, virtual photon (= tachyon ) does NOT exist in this model.
As shown in Fig.13, the average electron's momentum is zero, because the electron is moving around in circular orbit.
So, due to law of action and reaction, the whole atom is pushed in the opposite direction, or another light is emitted in the opposite direction to satisfy momentum conservation.
The relation between electron's moving direction and emitted lights are different from Compton scattering.
(Fig.14) Friction between electron's wave and field "pushes" out light.
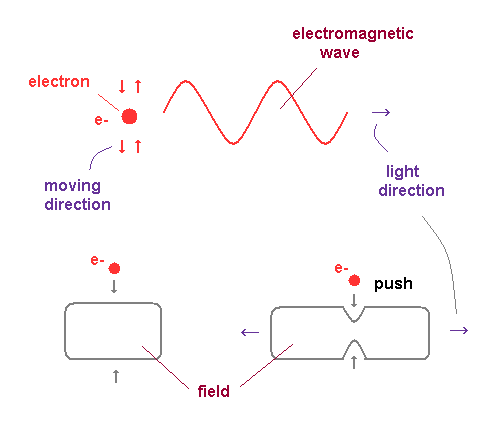
As shown in Compton scattering, the electromagnetic wave also has a property of de Broglie wave ( p = h/λ ).
Of course, the light is just an oscillation of fields ( NOT a particle ! ), so its propagating speed is always constant "c".
In the atomic orbitals, each electron is moving around a positive nucleus in a closed system.
This closed system means the average momentum direction of the electrons is zero ( up=down, left=right ).
So to satisfy total momentum conservation, the lights are emitted in both directions, which are perpendicular to the electron's motion (→ transverse wave ). And de Broglie waves are generated by electron's electric fields.
Each field (= de Broglie wave ) has periodically oscillating afterimage of electric field.
Depending on the magnitude of difference between the incident electrons and the surrounding field's state, the strength of friction and the energy of "pushed-out" electromagnetic waves are determined.
"Phase" difference between them (= electron and the field it hits ) determines emitted light's phase of electric field.
Unless we think about the concrete electric fields and de Broglie waves, virtual photon (= tachyon ) appears like quantum field theory.
(Fig.15) Friction between electron's wave and field "pushes" out light.
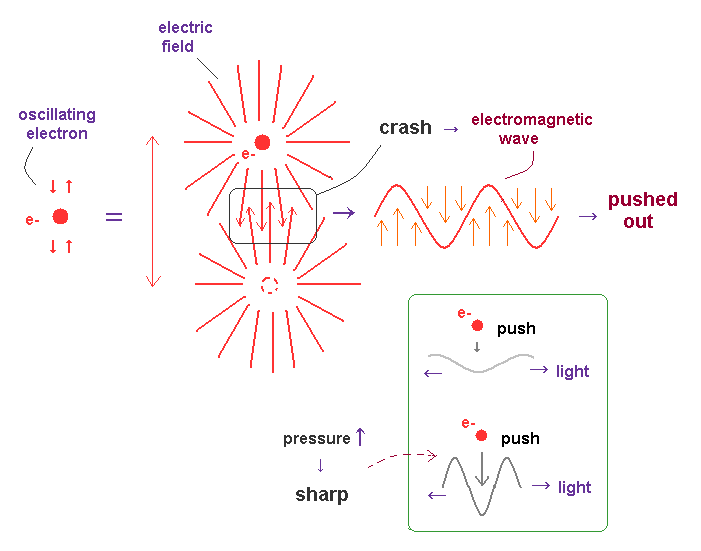
Basically, in circular or elliptic orbits, an electron is periodically moving (= oscillating ) in some closed system.
When its orbital length is just an integral multiple of de Broglie wavelength, their wave phase fit each other, and become stable.
In other cases, two de Broglie waves with different phases crash into each other, and its collision "energy" is radiated as a form of electromagnetic wave in the transverse direction.
As the impact of this collision (= friction ) is bigger, the generated "shock (= electromagnetic ) wave" becomes sharper (= short wavelength ), and it emits more wave energy.
As shown in Fig.15, almost vertical electric lines are on the front side of this collision between two waves.
So when this collided de Broglie waves (= consisting of vertical electric fields ) are pushed out, this wave becomes a transverse (= electromagnetic ) wave.
Due to the neutrality of the light and "positive" field (= ↑ ) attracting negative field (= ↓ ), the order of electric fields in light becomes (= ↑↓↑↓... ).
Of course, in circular orbit, when an electron rotating around a nucleus loses its angular momentum due to this collision between waves, some circularly polarized lights are generated.
(Fig.16) Straight and distorted electric fields cause different de Broglie waves.
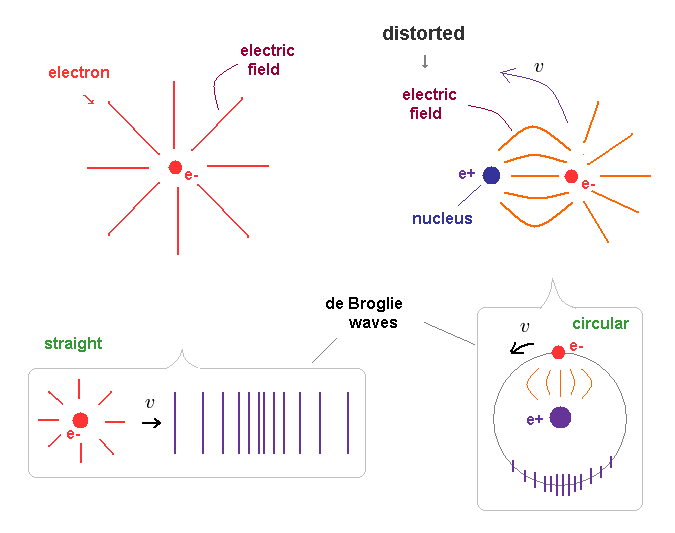
"Straight" electric fields spread in all directions around an free electron in Fig.16 left.
When this free electron is moving, it (= electron + electric fields ) generates "straight" de Brolgie waves.
On the ohter hand, the electric fields around a bound electron (= Fig,16 right ) are distorted and condensed on the side of positive nucleus.
So when this electron is moving around the nucleus, de Broglie waves becomes circular ( or elliptical ) along its path.
(Fig.17) Two wires carrying current in the same direction.
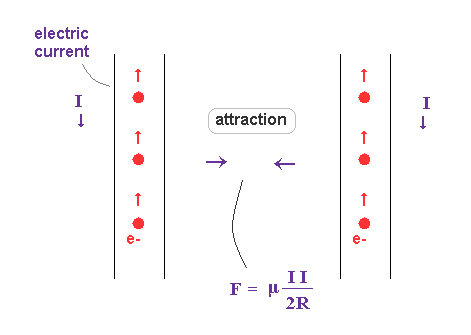
According to Ampere's ( or Biot-Savart ) law, two wires carrying current in the same direction attract each other.
Classical electromagnetism explains this phenomenon using magnetic force and right hand rule.
But as you know, the magnetic charge (= monopole ) does NOT exist. Only electric charge really exists.
So the magnetic force ( field ) has to be replaced by other realistic objects such as de Broglie waves.
(Fig.18) What is true nature of "magnetic" force ?
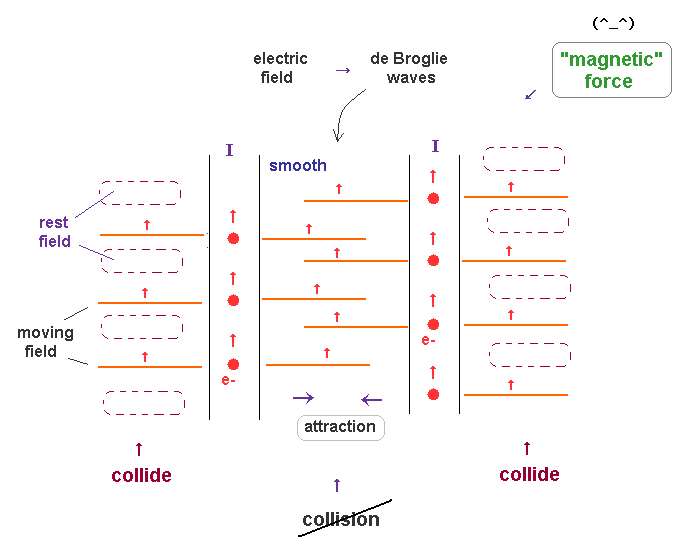
In Fig.18, two electric currents (= electrons ) are flowing in the same directions.
So these two electron's de Broglie waves are moving in the same direction, too.
Outside of these two current wires, each de Broglie wave always collides with rest surrounding fields. which causes some pressure.
On the other hand, between two currents, two de Broglie waves are moving together, and does NOT obstruct each other. In this area, pressure becomes lower.
As a result, two currents in the same direction attract each other.
This is thought to be true mechanisms of magnetic force ( field ), which is similar to Magnus effect.
(Fig.19) Electron's momentum ( p = mv ) and de Broglie wavelength (= λ ).

de Broglie wavelength (= λ ) is determined by the particle's momentum ( λ = h/mv ).
As a particle's momentum is bigger, the pressure it exerts on the surrounding fields becomes bigger.
So de Broglie wave means some pressure which the surrounding fields feel.
(Fig.20) Different substance's densities in the fields.
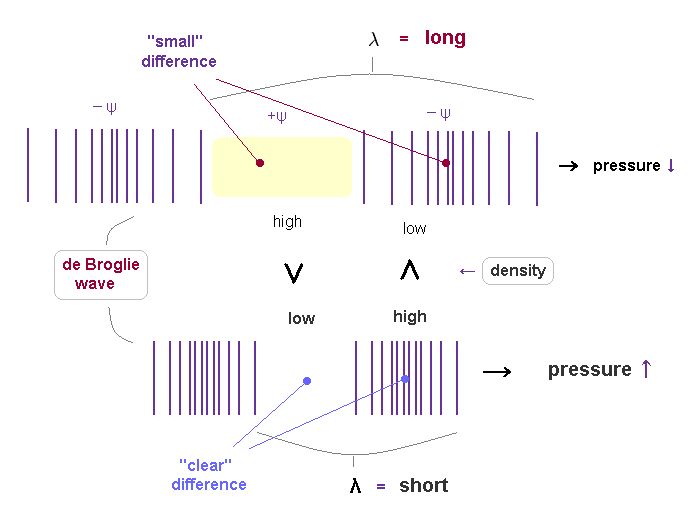
If de Broglie wavelength represents the strength of pressure given by a particle, their field's substance densities are thought to be a cause of this pressure.
Like classical "spring", as we apply stronger pressure, the field is more contracted and shorter.
A particle with more momentum exerts stronger force on the field, which causes more contraction of the field (= spring ).
As de Broglie wavelength is shorter, it means more field's substance is pushed out, so its density ( in -ψ ) is higher.
( So, conversely, in +ψ phase, the density of shorter de Broglie wave is lower ).
There is a bigger difference of field's density between ±ψ phases in shorter de Broglie wave.
This bigger difference of density between ±ψ is a motive force to pull "back" fields stronger and faster, which generates continuous shorter wavelength.
(Fig.21) Even when the momentums are the same, their velocities are different.
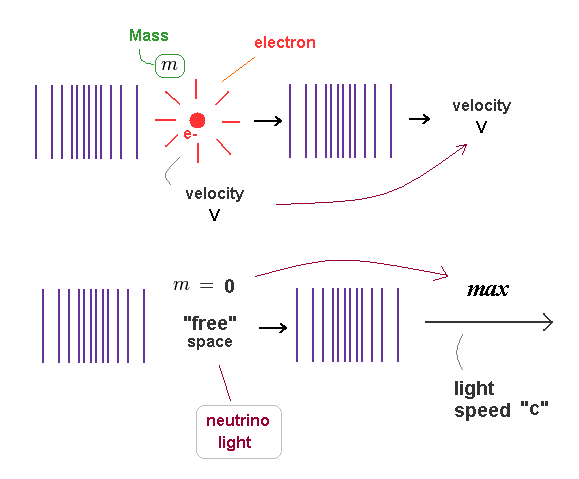
de Broglie wavelength is determined by a particle's momentum ( λ = h/mv ).
So particles with different "masses" (= m ) cause de Broglie waves with different speeds (= v ), even when their momentums ( p = mv ) are the same.
de Broglie wave's contraction is caused by a pressure of a particle.
So the wave's contraction is moving at the same speed with a particle which is constantly affecting the field.
As more field's substance is pused out towards the front, more other substances flow into the original place, which cause the same wavelength.
( This mechanism is the same as classical waves ).
Neutrino and electromagnetic waves have NO mass.
So their de Broglie waves propagate at light speed "c" ( or depending on the medium ).
So "mass" is related with something's density difference which generates "resistance", when it is moving through the surrounding field.
(Fig.22) "Positive" proton is much heavier than "negative" electron.
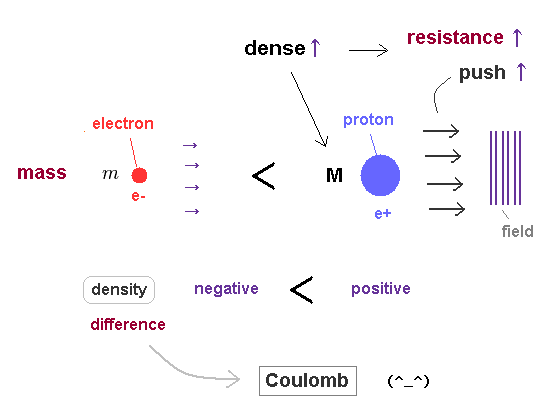
As a mass of a particle is bigger, its density becomes higher, and it can push away more field's substance at once.
So even when their velocities are the same, massive particle causes more contraction and resistance.
This is a reason why particles with different masses cause the same de Broglie wavelength, when they are moving at different speeds. ( when their momentums p = mv are the same. )
Considering the fact that "positive" proton is much heavier (= denser ) than "negative" electron, the difference between positive and negative charges depends on density difference between things foming ± charges.
The pressures in all fields tend to be uniform due to the equilibrium of forces.
So, the substance in high density, high pressure (= positive charge ) field tries to flow into low density, low pressure (= negative charge ) field, which expresses opposite charges attracting each other.
(Fig.23) de Broglie relation.
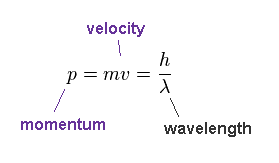
According to de Broglie relation, the momentum ( p = mv ) is expressed as ( p = h/λ ).
Here, p = momentum, m = mass, v = velocity, h = Planck constant, λ = wavelength.
As shown on this site, total energy (= E ) of electromagnetic wave is linearly proportional to frequency (= f ) through the relation of E = hf, which is confirmed in photoelectric effects.
Surprisingly, in any other particles such as electrons and protons, their frequency is proportional to their total energy, if de Broglie relation is satisfied !
(Fig.24) When electron's velocity becomes half ( v → 1/2 v ), its wavelength becomes twice ( λ → 2λ ).
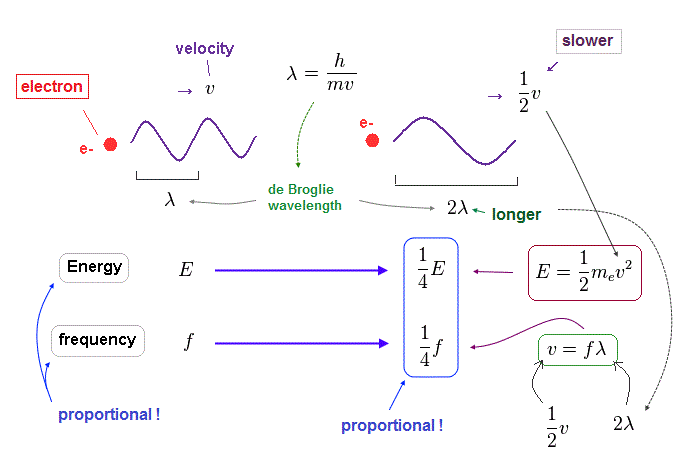
When an electron's velocty (= v ) becomes half (= 1/2 ), its total ( kinetic ) energy (= E ) becomes 1/4 of the original value, because E is proportional to a square of velocity ( E = 1/2 mv2 ).
According to de Broglie relation ( mv = h/λ ), the electron's wavelength becomes twice ( λ → 2λ ), when the velocity becomes half.
Considering wave relation ( v = fλ ), the electron's frequency (= f ) becomes 1/4 of the original value in this case.
As you see, also in electron's de Broglie wave, the energy is proportional to frequency ( E/f = constant ) !
(Fig.25) Momentum ( p = h/λ ) is constant.
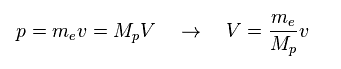
Here we think about the case when the momentum (= p ) is common in both of "light" electron and "heavy" proton.
So through de Broglie relation ( λ = h/p ), their wavelengths (= λ ) are the same, too.
Due to heavier mass ( Mp ) of proton, the velocity (= V ) of proton becomes much lower than that (= v ) of electron.
So the total kinetic energy ( E = 1/2 MpV2 ) of proton is much smaller than electron (= 1/2 mv2 ).
(Fig.26) Energy (= E ) is proportional to frequency (= f ) in electron and proton.
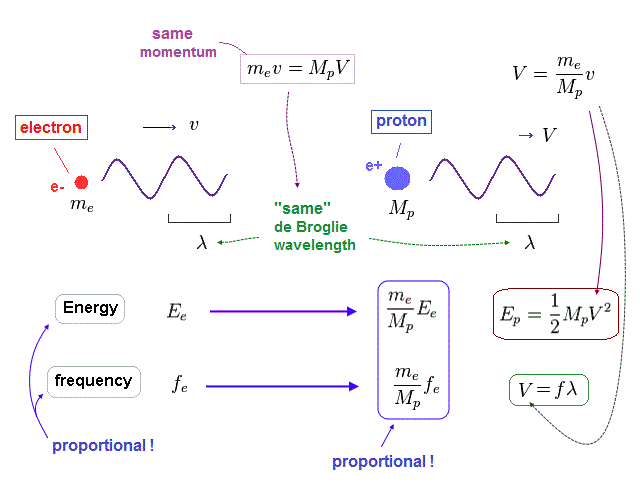
Again, through the wave relation of v = fλ, we can find the proton's frequency.
As shown in Fig.26, between proton and electron, the relation of energy (= E ) proportional to frequency (= f ) holds true.
So not only in electromagnetic wave but also in electrons and protons, the frequency has an important meaning to determine their total energy.
(Fig.27) Total energy in electron and proton.
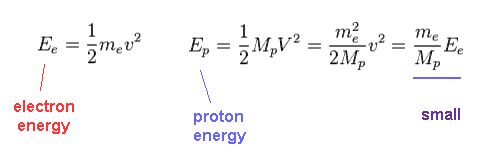
Using Fig.25, we find the proton's kinetic energy is much smaller than electron due to its large mass, even when their momentums are the same.
(Fig.28) Ratio of electron's to proton's masses.
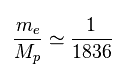
Proton (= Mp ) is much heavier ( 1836 × ) than electron's mass (= me ).
(Fig.29) Frequency = velocity / wavelength.
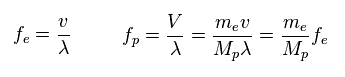
Through wave relation, we find the proton's frequency becomes much smaller than electron.
( Here the wavelengths ( momentums ) of electron and proton are the same. )
(Fig.30) Light's energy is proportional to its frequency, too.
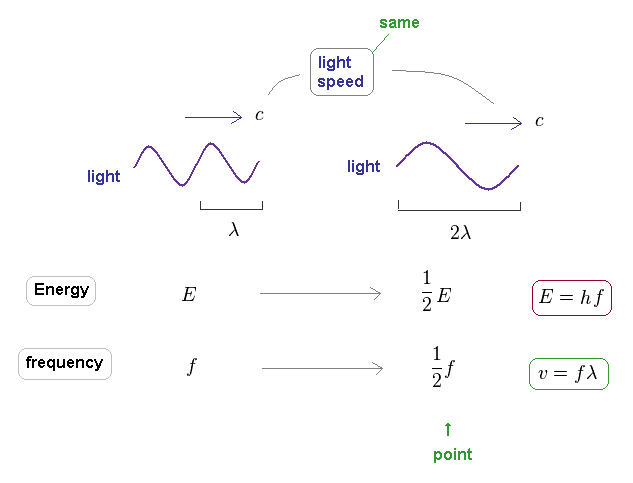
It is known that light's energy is also proportional to its frequency through the relation of E = hf.
The important point is that the speed of the light is always constant "c", different from other particles.
This means there is NO concept such as "acceleration" in light ( and neutrino ).
When electron's ( or proton's ) wavelength changes, both of its velocity and momentum changes.
So the electron's frequency is inversely proportional to a square of wavelength, as shown in Fig.24.
On the other hand, due to neglecting light speed change, the light frequency is just inversely proportional to its wavelength.
As you see, de Broglie wavelength ( λ = h/p ) expresses "contraction" ( or expansion ) of the field by the momentum (= impulse ), compared to its equilibrium state, irrelevant to the velocities of various particles.
(Fig.31) Mechanism of Coulomb force.
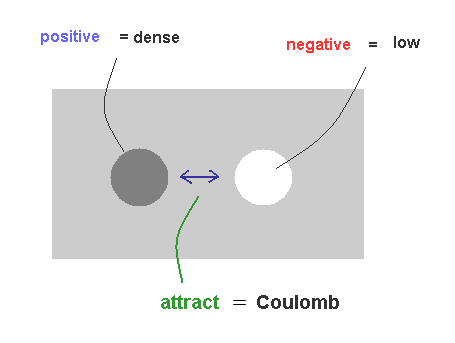
As I said in Fig.22, it is natural that we think the big difference between proton's and electron's masses is related to Coulomb force.
Basically, to keep equilibrium, high density (= positive charge ) substance tries to flow into low density (= negative charge ) field, which can explain the true mechanism of Coulomb force, NOT relying on unrealistic virtual photons.
Conversely, between high-high densities and low-low densities, they exert "replusive" force, due to their more unbalanced states.
(Fig.32) When electron approaches proton, their kinetic energy becomes larger.
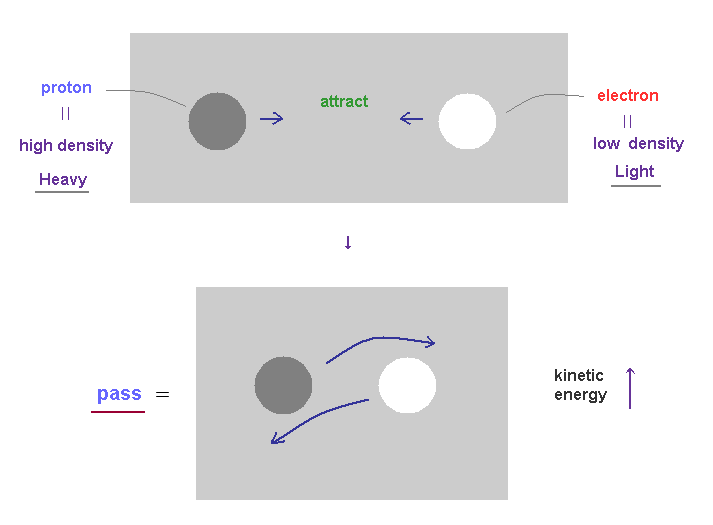
As you know, total energy must be always conserved.
The displacement and unbalanced states ( between ±charges ) of the field cause some potential energy.
When positive proton attracts negative electron, they (= mainly light electron ) are accelerated and their kinetic energies become larger, replacing the original potential energy.
As a result, positive proton and negative electron can NEVER fuse into one, due to their larger kinetic energy.
( Very unstable antiparticles such as positron contradict basic physical rules, and are completely unreal. )
(Fig.33) Like spring expanding and contracting, the field displacement (= charge ) is conserved.
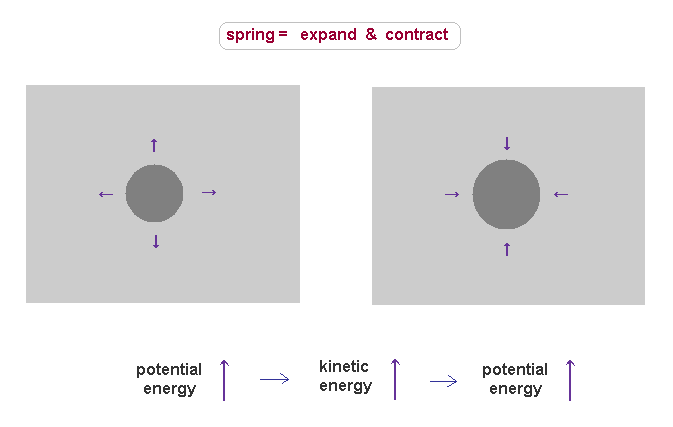
For example, in positive proton charge, its field is thought to be denser than the surrounding field.
This state causes large potential energy due to its unbalanced density.
Once they get potential energy, this energy must be conserved.
When these dense substances try to spread out due to their density defference, they are accelerated.
In this process, the field around the proton is contracted (= denser ), which causes new resistance to push them back.
On the other hand, the density inside proton becomes lower than the original value, which tries to pull them back.
As a result, these substances return to the original dense field, obeying the conservation of total energy, which means total ±charges are conserved.
(Fig.34) What is the electromagnetic wave ?
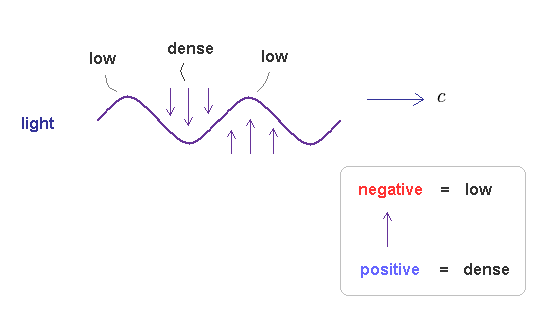
As I said in Fig.15, the electromagnetic wave is thought to be emitted (= pushed out ) in transverse direction, when two de Broglie waves (= energy, electric field ) crashes.
Due to neutrality and positive field (= ↑ ) attracting negative field (= ↓ ), this "pused out" electromagnetic wave becomes a repetition of ↑ and ↓.
As I said, we can think positive field is denser than negative field.
So the electromagnetic wave consists of a repetition of low and dense fields, like usual de Broglie waves.
This is the reason why electromagnetic waves also satisfy de Broglie relation (= confirmed by Compton effect ), though it is "transverse" wave (= a "special" type of complex de Broglie wave ).
(Fig.35)
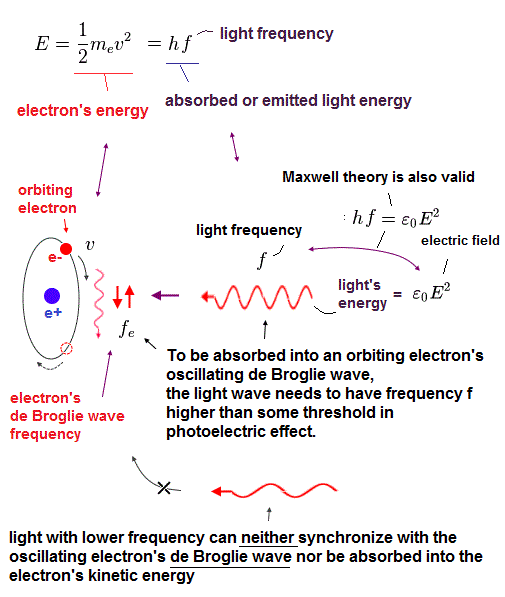
Here we investigate the relation between electron's frequency (= fe ) and emitted light's frequency (= f ).
In Fig.35, total kinetic energy of electron (= 1/2mv2 ) is equal to light's energy (= hf ) emitted from the electron.
(Fig.36)
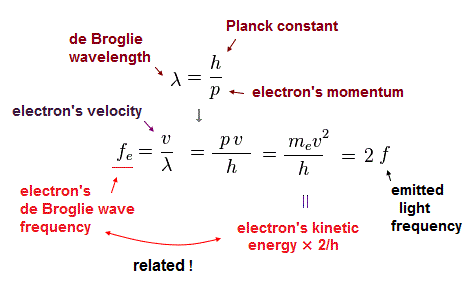
Using wave relation ( v = fλ ) and de Broglie relation ( λ=h/p ), we find that the electron's ( de Broglie ) frequency (= fe ) is two times bigger than the emitted light frequency (= f ).
(Fig.37) Oscillating electron emits light and gradually loses its energy.
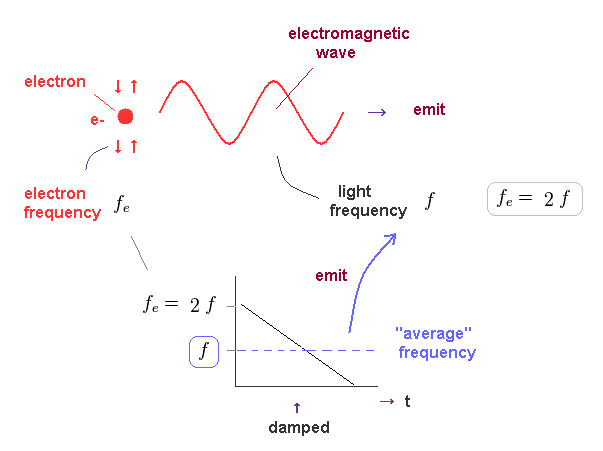
In Fig.37, we think about the case in which oscillating electron gradually emits light and loses its kinetic energy.
The initial electron's frequency is equivalent to 2 × f (= emitted light frequency ), as shown in Fig.36.
The more light the electron emits, it loses more energy, and its oscillation becomes slower ( to be zero ).
It means the average electron's frequency becomes half of the original value (= 1/2 × fe = f ) .
As a result, we can prove there is an important relation between electron's and emitted light frequencies.
(Fig.38) Transition from excited ( n = 2, f=4 ) state to ground state ( n =1, f = 2 ).
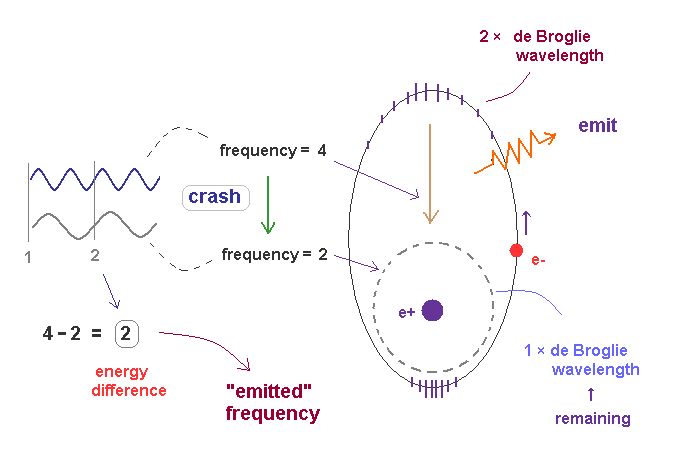
In Fig.38, the excited state of 2 × de Broglie wavelength returns to ground state (= 1 × de Broglie wavelength ).
Accelerated by Coulomb force, the final frequency of de Broglie wave of excited electron becomes f = 4.
The frequency of remaining ground state de Broglie wave (= 1 × wavelength ) is f = 2.
These two de Broglie frequencies before and after transition are different, so they don't fit each other.
The crash between these two de Broglie waves causes swell with the frequency ( 4-2 = 2 ), which is the difference between two states.
The excited de Broglie wave is attenuated, while it emits light.
So the average frequency of emitted light becomes half of 2 (= 1 ), as is explained in Fig.37.
(Fig.39) Mass (= m ) on spring is oscillating up and down.
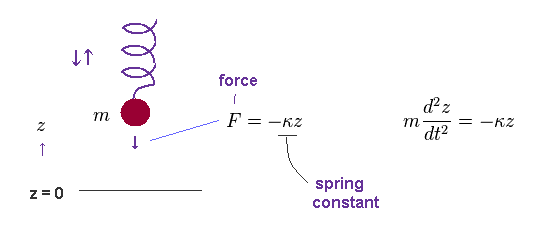
According to Hooke's law, the force (= F ) acting on a object with mass (= m ) is given by F = -κ z, where κ is spring constant, and "z" is displacement from its equilibrium position.
(Fig.40) Spring's frequency (= f ).

Solving Fig.39, we obtain Fig.40.
As you see, the angular frequency (= ω ) is determined by spring constant (= stiffness, κ ) and mass, NOT by its amplitude (= A ).
(Fig.41) Total energy E.
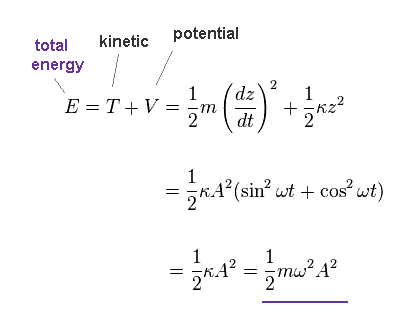
Total energy (= E ) is given by the sum of kinetic (= T ) and potential (= V ) energies.
As shown in Fig.41, this total energy is determined both by angular frequency (= ω ) and amplitude (= A ).
(Fig.42) Propagating transverse wave = collection of small springs..
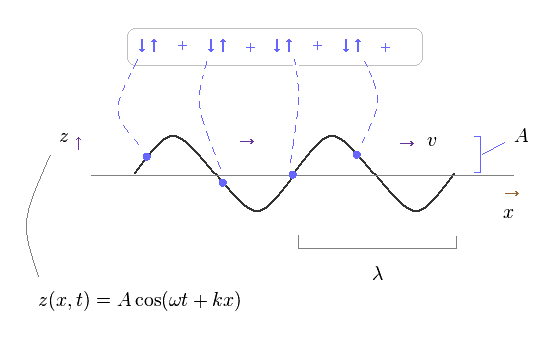
Basically, propagating waves are considered to be a collection of simple harmonic oscillators of each field, as shown on this site.
So, though a whole wave looks like it is propagating in one direction, each field is NOT moving in that direction.
Each field is just oscillating up and down ( or left and right ).
(Fig.43)
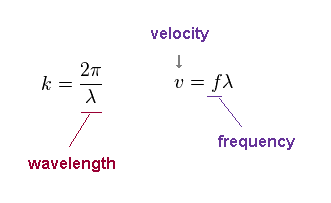
"k" is wavenumber, given by 2π/wavelength (= λ ).
The wave velocity "v" is fλ, where "f" is frequency.
Note that this wave velocity is just phase velocity, which is NOT the oscillating velocity of each field.
Even if each field is oscillating slowly, the phase velocity can be higher, when its wavelength is long.
(Fig.44) Each field is oscillating in parallel to the direction of wave propagation.
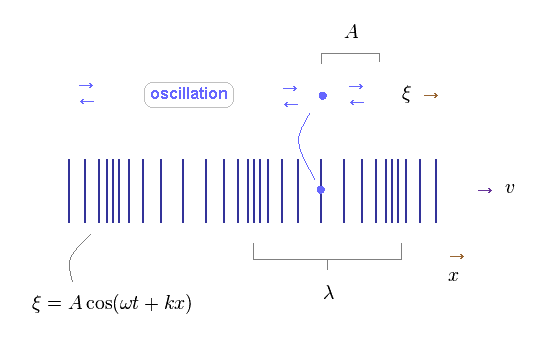
Different from transverse wave, each field of longitudinal wave is oscillating in parallel to the direction of wave propagation.
The basic relations of harmonic oscillator are the same in both types of waves.
(Fig.45) Density (= pressure ) change within field with the volume of 1 × Δx.
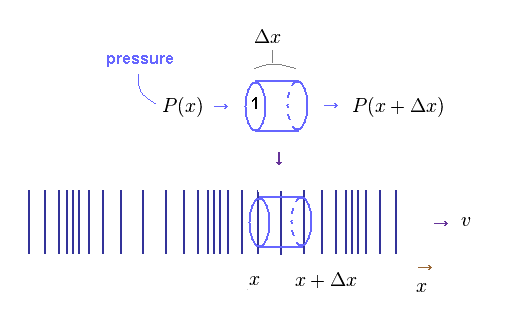
Here we derive the relation of simple harmonic oscillator also in longitudinal wave.
In Fig.45, pressure (= P ) acts on the columnar field with the volume of 1 × Δx.
X-coodinate of both ends in this field is "x" and x+Δx.
(Eq.1) Pressure and density of field.
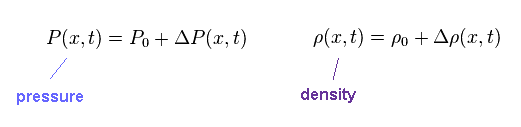
Pressure (= P ) and density (= ρ ) of each field is given by Eq.1.
P0 and ρ0 represent "average" pressure and density, respectively.
(Eq.2)
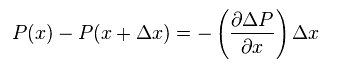
The total force acting on the above field is given by the difference between pressures at "x" and "x+Δx".
(Eq.3)
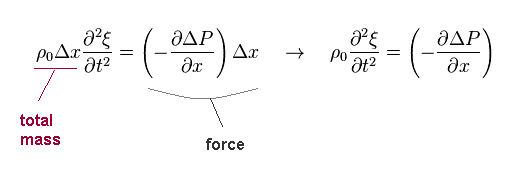
Total mass included in the above field is ρ0Δx ( base area is "1" ).
So the equation of motion is given by Eq.3.
(Eq.4)
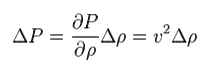
Pressure is thought to be proportional to density.
The ratio of them is supposed to be "v2". So,
(Eq.5)
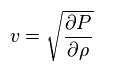
Volume (= V ) change is given by
(Eq.6)
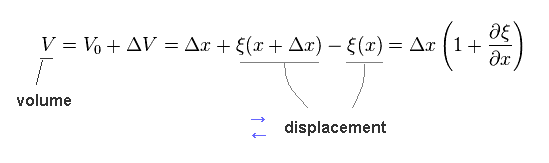
Total amount of substance inside the field is constant, so,
(Eq.7)
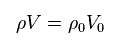
From Eq.6 and Eq.7, we have
(Eq.8)
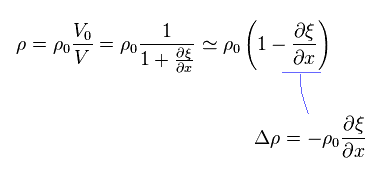
From Eq.3, Eq.4 and Eq.8, we can get the usual wave equation of
(Eq.9)
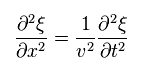
where
(Eq.10)
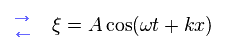
and
(Eq.11)
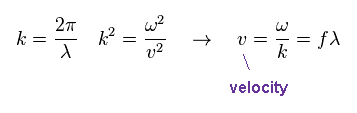
As you see, longitudinal wave such as sound is the same as transverse wave (ex. light ) in their mechanism of field oscillation.
(Fig.46) Container including N moving particles.
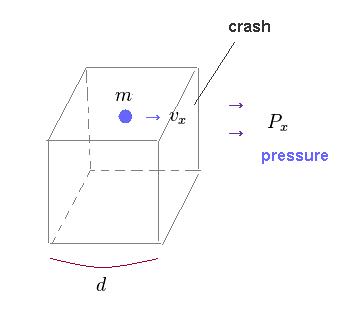
In this section, we prove that the same pressure is generatad, when the same amount of energy is given, irrelevant to substance density (= negative or positive ).
Due to this mechanism, an integer multiple of de Broglie wavelength around some nucleus is precisely satisfied.
(Eq.12)
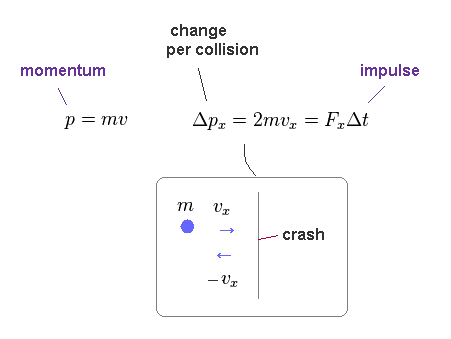
Like on this site, each particle (= field substance ) is moving with velocity "v".
Its momentum in x direction is mvx.
After it collides with one side of this container, this particle will have a momentum of -mvx.
The magnitude of the change in direction is "2mvx", which means "impulse" (= FΔt ) applied to that side.
(Eq.13)

Per one collision, the particle has to go and return (= the distance of "2d" ).
So, the mean time per collision is given by Eq.13.
(Eq.14)
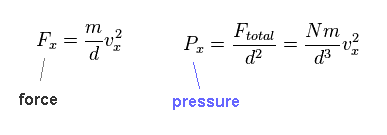
From Eq.12 and Eq.13, we fine force (= Fx ) acting on the side becomes like Eq.14.
Pressure is given by F/area (= d2 ).
Here "N" particles are included inside this container.
"n" is the number density, "v" is the total velocity of each particle.
(Eq.15)
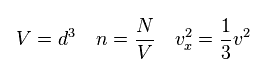
From Eq.14 and Eq.15, we obtain
(Eq.16)
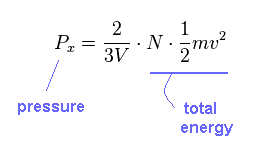
As you see, pressure (= P ) is proportional to total energy, irrelevant to the particle's number (= N ).

2014/10/22 updated. Feel free to link to this site.