QED is wrong, unable to predict anomalous magnetic moment by its fake trick.

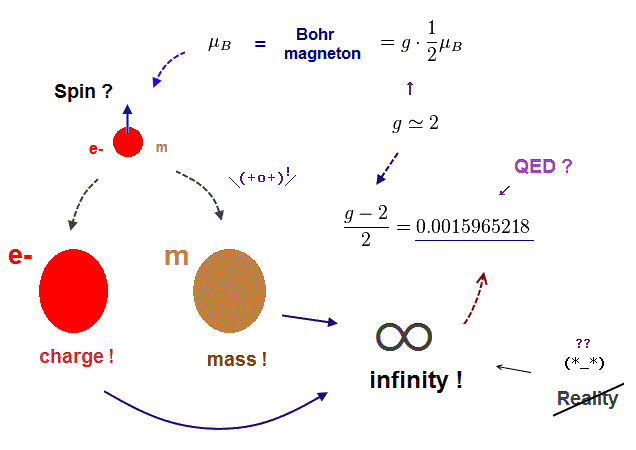
Home page
Calculation of QED g-factor.
Einstein relativity is false.

QED always gives useless infinities which must be illegitimately removed by renormalization based on illusory infinite bare mass and charge.

(Fig.1)  A electron's bare charge and mass must be infinite to cancel QED meaningless infinities and artificially get finite g-2 (= anomalous magnetic moment ) values.

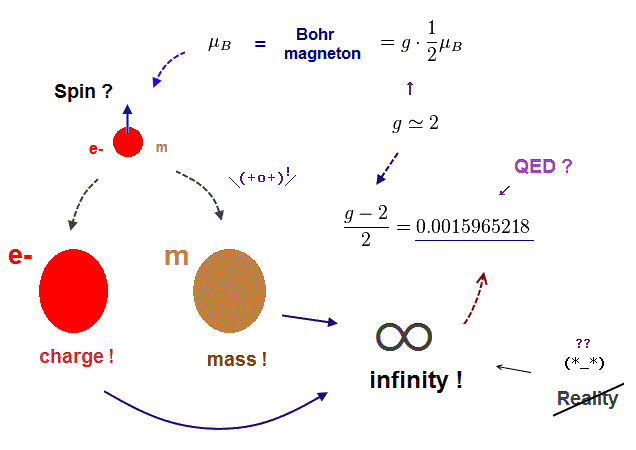
(Fig.2)  QED renormalization just illegitimately removes infinities.

QED is useless, unreal, always giving infinities by its unreal virtual particles.

Contrary to the media-hype, quantum electrodynamics (= QED ) is an unsuccessful, unreal, useless theory.

Relativistic QED says the vacuum is filled with unphysical virtual photons with imaginary mass, which paradoxically disobey Einstein relativistic mass-energy relation, to mediate electromagnetic force ( this-p.3 ).

These infinite (unreal) virtual particles make all QED calculations give meaningless infinities ( this-3rd-paragraph,  this-3rd-paragraph ).

QED useless infinities must be artificially removed by illegitimate renormalization, which invalidates QED.

↑ These QED meaningless infinities must be artificially removed by the illegitimate math trick called renormalization to get some finite values of electron's anomalous magnetic moment (= g-2-factor ) and Lamb shift.

This QED renormalization artificially removing infinities to illegitimately get some desired finite values is harshly criticized even by founders such as Dirac and Feynman as "hocus-pocus" or "dippy process ( this-A. Historical introduction,  this-1st-paragraph )".

This-p.1-right-2.2~p.2-left says
"Unfortunately, QFT (= quantum field theory or QED ) was a complete failure since any attempted calculation under this theory resulted in an (meaningless) infinite number"

"Separation: separating an infinite series into two components, one that diverges to infinity and another that converges to a finite value. Eventually, the infinite component is ignored and only the finite part (= anomalous magnetic moment ) remains"  ← QED is a wrong math.

QED needs unreal infinite bare charge and mass of an electron to cancel infinite virtual particles.

According to the unphysical QED, the bare charge and mass of an electron must be unrealistically infinite to cancel the infinities caused by infinite virtual particles ( this-p.3-5,  this-middle,  this-p.19-3rd-paragraph,  this-middle ).

This QED math based on infinity minus another infinity giving some finite physical values is clearly wrong and illegitimate.

↑ According to legitimate math, "infinity minus infinity" becomes a "uncertain indeterminate number" that cannot determine some physical values, so QED renormalization artificially removing infinities is Not a right math.

QED is useless, unable to predict anything.

Not only the electron's anomalous magnetic moment but also tiny Lamb shift in QED is also an artificial illegitimate manipulation irrelevant to QED prediction as this-p.3-left-6th-paragraph says
" His calculation (= of Lamb shift ) included this value that we suspect that was entered ad hoc to match the theoretical value with the experimental value. In the field of physics, this trick is known as a 'fudge factor'."

If QED was really successful or useful, almost everybody should have already known how to calculate the anomalous magnetic moment by such a (wrongly) successful QED.  ← But actually, ordinary people (even physicists) do Not know any QED (meaningless) calculation methods based on (unreal) virtual particles ( this-p.5-right-1st-paragraph, p.6-(22) ), which fact shows QED is useless, unreal.

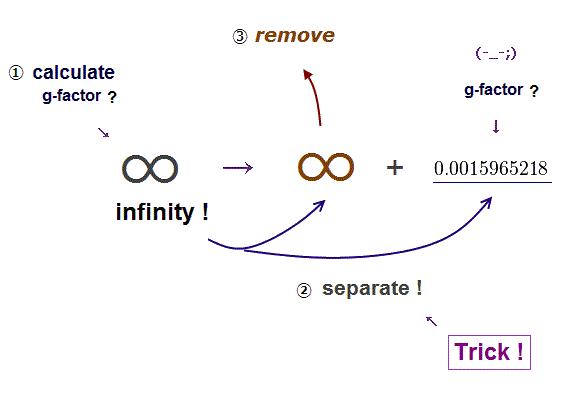
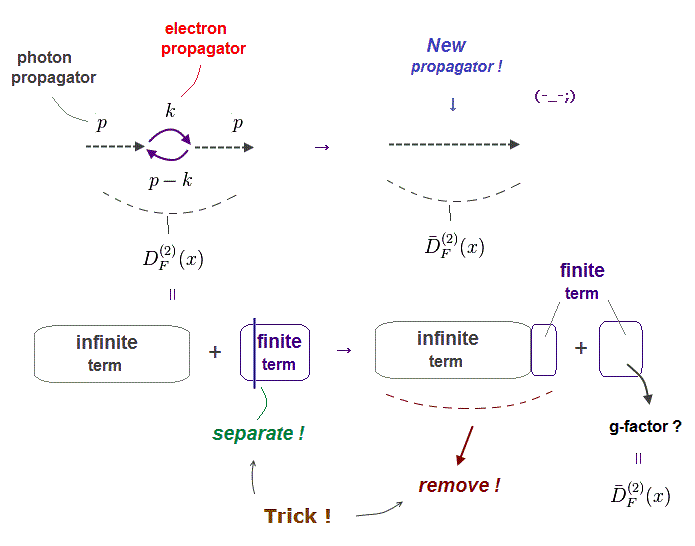
(Fig.3)  QED unreal virtual electrons and photons are expressed as unphysical math relations called propagators that are used as a tool to artificially manipulate anomalous magnetic moment value.

QED just manipulates unphysical math called (virtual particle) propagators to illegitimately get anomalous magnetic moment.

The (unphysical) QED is rather simple, consisting only of illusory virtual electrons and photons with energies (or momentums ) from minus infinity to plus infinity, which QED unphysical calculations always diverge to meaningless infinities by integration ( this-p.8-upper,  this-p.68(or p.64),  this-p.6 ).

In the unphysical QED rule based on abstract Feynman diagram relating (illusory) photons to electrons, these virtual electrons (= S_F ) and virtual photons (= D_F ) are expressed as unphysical math relations called propagators of (illusory, virtual) photons ( this-p.2-4,  this-p.2-3 ) and fermions (= virtual electrons,  this-p.9-10,  this-p.2 ).

Here "p" represents a (virtual) particle's relativistic momentum and energy,  κ represents the electron's mass,  λ represents the photon's mass (= this λ should be close to zero ).

These virtual photons and electrons are known to disobey Einstein relativistic energy-mass relation ( this-p.9-10,  this p.6 ), disproving relativistic QED,

QED is bad, just artificially manipulating electron's anomalous magnetic moment's value by wrong math artificially removing unneeded parts, which is Not prediction.

(Fig.4)  QED just artificially changes equations and removes the unneeded part by illegitimate renormalization to get finite anomalous magnetic moment.

QED uses wrong math to artificially fit the calculated electron's anomalous magnetic moment value to the experimental value.

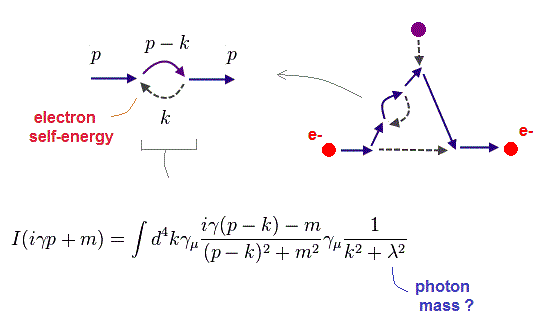
Fig.4 is part of electron's anomalous magnetic moment (= g-factor ) allegedly caused by the unreal virtual photons and electrons ( this p.9-10,  this-p.6-8 ) in the two-loop or fourth-order correction calculated by Karplus and Kroll in 1950 ( this p.24,  this-p.10-11 ).

The first calculation (of one loop correction of anomalous magnetic moment ) by Schwinger no longer agreed with the new experimental result, so Karplus and Kroll tried to artificially fit the newly-calculated two-loop correction (= fourth-order ) of anomalous magnetic moment with the new experimental value.

↑ Later, after the newer experimental result of the anomalous magnetic moment turned out to disagree also with the new Karplus, Kroll's calculated results, they started to say their (artificial) calculations of Fig.5 might be wrong (= Fig.4 calculation remained as a right one ).

↑ This infamous unscientific story showed QED is just an illegitimate math trick artificially fitting calculations with new experimental results ( this-p.5-right-6.1~ p.6 ), each time the previous artificial QED calculated values turned out to disagree with the new experimental values.

Artificially change the equation by wrong math → remove only the unneeded part by renormalization, which is Not QED prediction.

This Karplus and Kroll's paper ( p.2-Fig.1-IId, p.5-right~lower,p.7, p.10-M^IId, p.12,14-μ^IId ) explains the detail of Fig.4's calculation of part of anomalous magnetic moment based on (unreal) virtual photons and electrons.

In this (artificial) calculation process of the anomalous magnetic moment's two-loop correction, they deliberately used a wrong math in calculating this-p.6-equations (21) and (22) (= this (21) is Not equal to (22) as shown in Fig.4-artificial illegitimate change, contrary to the paper's claim, without some unspecified artificial new rules ).

↑ After this wrong math illegitimately changing the equation, only one term of this artificial equation-(22) in p.6 (= Fig.4's equation surrounded by the square ) was used as part of anomalous magnetic moment in M^IId in this-p.10, and all other parts (= including divergent and non-divergent parts ) were artificially removed by the illegitimate renormalization based on illusory infinite bare charge or mass.

This-p.7-left-2nd-paragraph says
"The fact that B is infinite,.. it can be interpreted as a charge renormalization (= the first part of I was artificially removed by using the unreal infinite bare charge )"

QED just artificially separates the unneeded and the needed parts by illegitimate change of variables and ad-hoc renormalization, which is Not prediction.

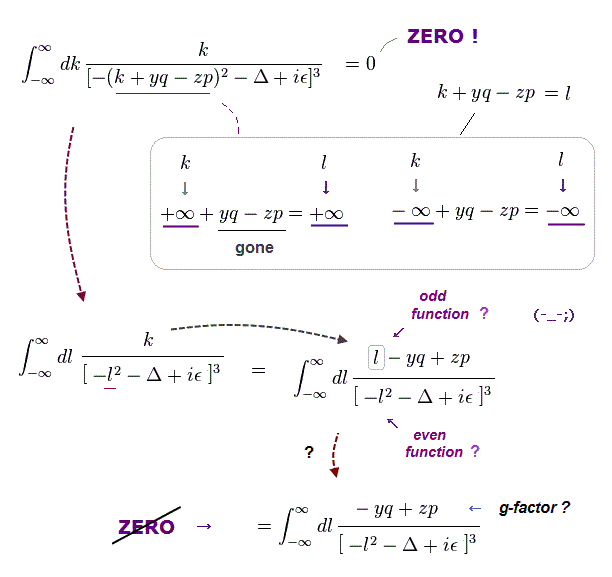
(Fig.5)  QED math trick: artificial change of variables → remove only the unneeded part by renormalization, which is Not prediction.

Change of variables → artificially separate, remove the unneeded part by renormalization.  = QED illegitimate math trick

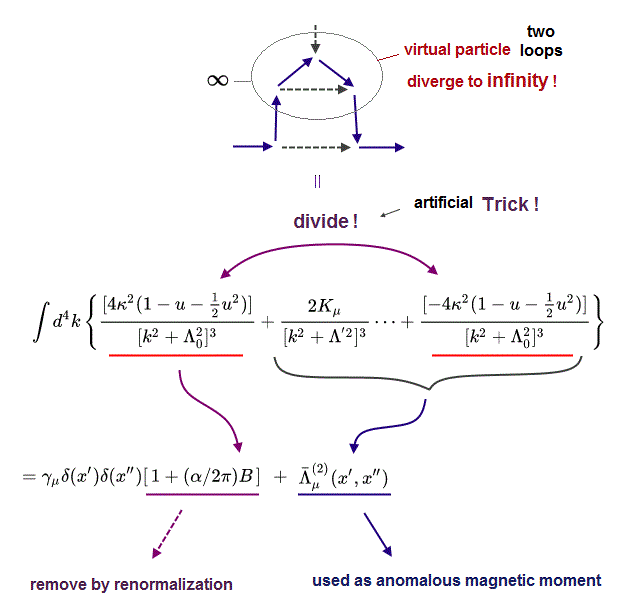
Fig.5 is QED artificial math trick in another part of electron's anomalous magnetic moment's two-loop correction ( this-p.2-Fig.1-IIc, p.8, p.9-upper, p.10-M^IIc, p.14-μ^IIc ).

This-p.8-(29) conducted the artificial change of variables, and then separated, removed only the unneeded part of B in the final anomalous magnetic moment part of M^IIc in p.10.

This-p.9-2nd-paragraph says
"Here again the separation of the renormalization term B has made the physically significant correction divergent ( this-p.2-3rd-paragraph )"

↑ This Karplus, Kroll (artificial) calculation of electron's anomalous magnetic moment's two-loop (= fourth-order ) correction almost agreed with the experiment at first.

But later, after a newer experimental result turned out to disagree with this Karplus, Kroll's calculation, they started to say there might be some calculation mistake, and artificially changed (= manipulated ) the calculated result, which is illegitimate, Not a QED prediction at all ( this-p.5-6.1-p.6 ).

After Petermann's new (unpublished) calculation, Fig.5 calculated result (= μ_IIc ) was artificially changed, and Fig.4 result (= μ_IId based on wrong math disproving QED's anomalous magnetic moment ) remained, unchanged ( compare this-p.2 and this-p.14 )

(Fig.6)  QED depends on illegitimate change of variables and renormalization of infinities to artificially generate some finite physical values.

QED unphysical math trick = change of variables, artificially separate, remove only an unneeded part.

Contrary to the hypes, QED calculation is unsuccessful, wrong, giving only meaningless infinities.

QED often uses the artificial math trick of change of variables.

↑ "Change of variables" itself originally should not change the results themselves, which is Not the case of QED that artificially separates and removes the unneeded part artificially.

In order to obtain the desired anomalous magnetic moment value, QED artificially separates and removes only the unneeded part by the illegitimate renormalization ( this-p.6-1st-paragraph, p.7-left-2nd-paragraph, p.8-(29). p.9,  this-p.26-A.28 ).

So by combining the change of variables with the illegitimate renormalization, QED can artificially manipulate the finite results as free parameters, which shows QED is unsuccessful with No ability to predict any physical values.

Feel free to link to this site.