Top page valence electron
Bohr model Neon structure.
New Bohr's molecular bonds.
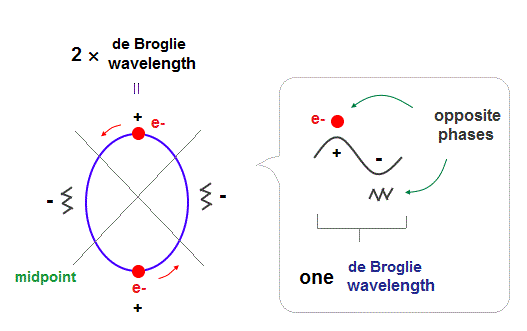
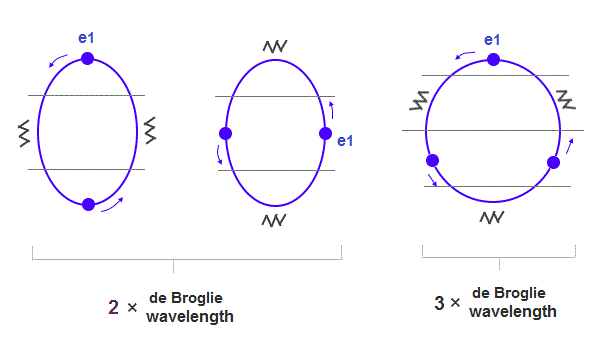
(Fig.1) 2 × de Broglie wavelength orbits. Each is a pair of opposite phases.

One wavelength consists of a pair of "crest" (= + ) and "trough" (= - ) irrespective of transverse and longitudinal waves.
Here we suppose "+" phase contains an electron itself, and "-" phase is compressed by the electron's movement, --- which is " de Broglie wave ".
2 × ( 1 × ) de Broglie wavelength orbit contains two ( one ) pairs of ±opposite phases and two ( one ) midpoint lines.
These "opposite" wave phases cancel each other by destructive interference.
To avoid it, two orbits must cross perpendicularly.
(Fig.2) Maximum orbits = midpoint lines + 2 (= two perpendicular orbits )
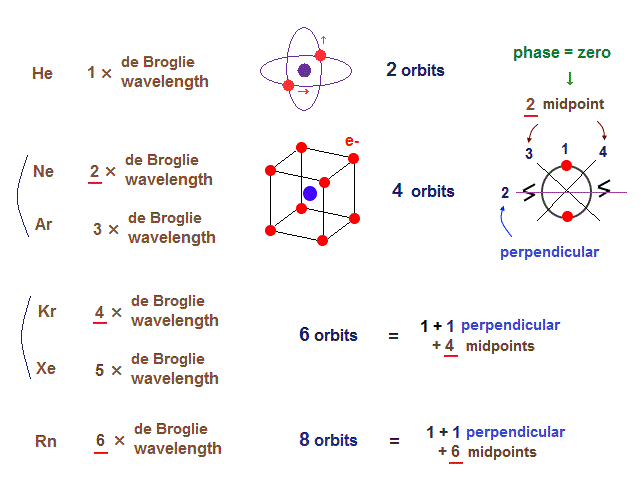
As shown on this page, the number of midpoint lines ( related to de Broglie wavelength ) influences the number of maximum orbital number in the periodic table.
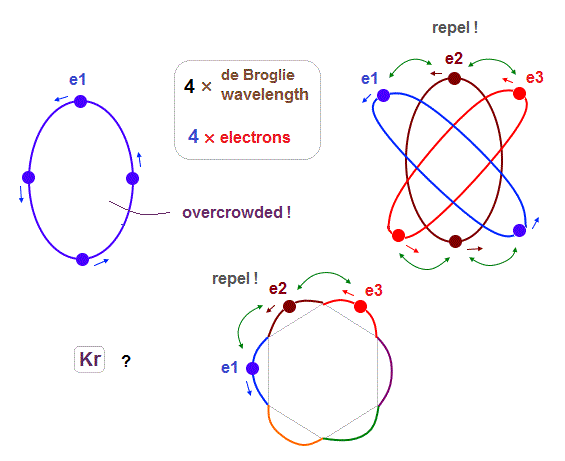
The maxium number of orbits in Ne becomes "4" (= 2 × perpendicular + 2 × midlines ).
4 × de Broglie wavelength contains 4 midlines, so the total orbital number of Kr becomes "6".
The odd numbers of "3", "5", "7" orbits are asymmetrical and unstable.
So the orbital numbers of "Ar" (= 3 × waveslength ), "Xe" (= 5 × waveslength ) remain the same as "Ne" and "Kr".
(Fig.3) "Opposite" wave phases interfere with each other, destructively. → "perpendicular".
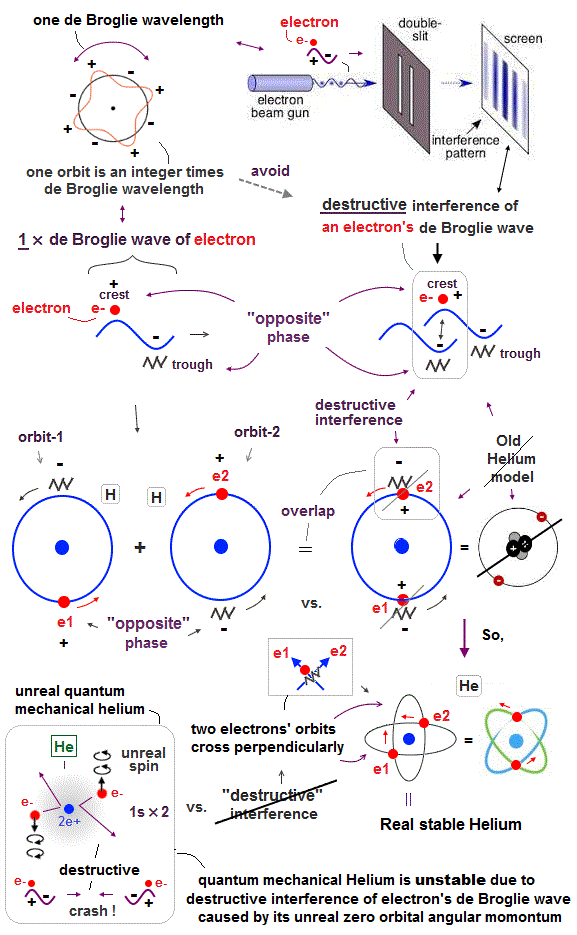
Helium atoms contains two 1 × de Broglie wavelength orbits ( n = 1 ).
So, two opposite wave phases cause "destructive" interference and instability.
To avoid this destructive interference, two orbits of helium have to cross each other "perpendicularly", because "perpendicular" means each wave phase can be independent from another.
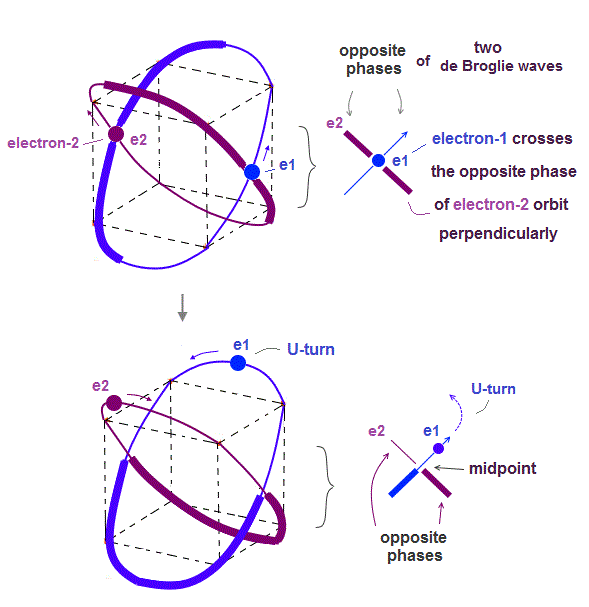
(Fig.4) Two electrons have to pass each other on "midpoint" lines.
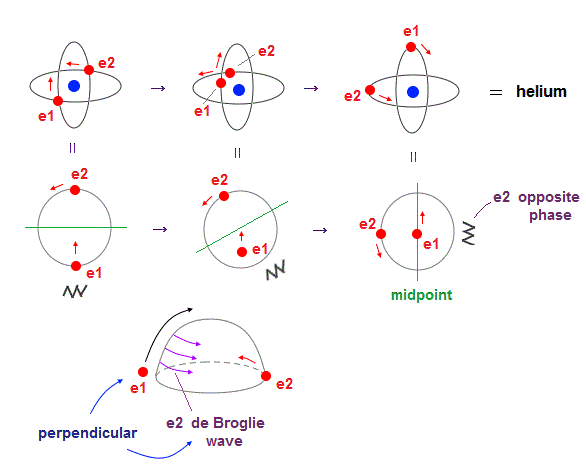
In one de Broglie wavelength orbit, a half of it is "opposite" wave phase.
So, "e1" electron of Fig.4 must go in the direction perpendicular to "e2" orbit to midpoint.
Two electrons in "perpendicular" orbits have to pass each other in the "parallel" direction at "midpoint", because "midpoint" line is zero phase, which has NO influence on another wave.
(Fig.5) If Beryllium is composed of four 1 × de Broglie wavelength orbits ?
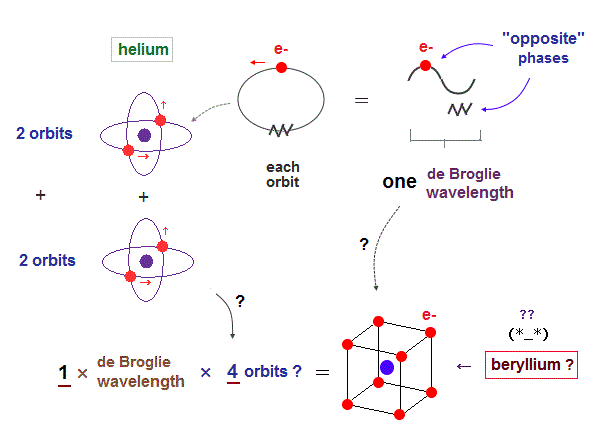
As I said in Fig.2, the maximum orbital number in 1 × de Broglie wavelength is "two" of helium. It's impossible for atoms (= beryllium ) to contain four 1 × de Broglie wavelength orbits.
Here we explain this Pauli exclusion principle from the viewpoint of de Broglie wavelength.
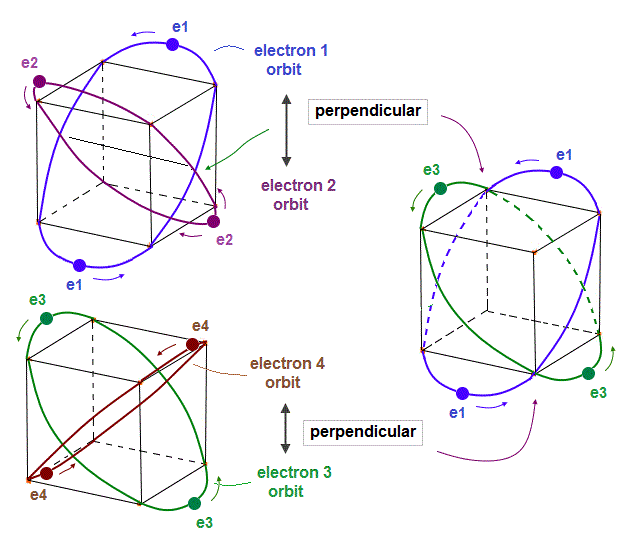
(Fig.6) 2 × two helium orbits perpendicular to each other = beryllium ?
In helium-like atoms, e1 and e2 ( e3 and e4 ) orbits cross perpendicularly.
Here we try to combine these four orbits to make beryllium outer-electron orbits.
(Fig.7) If beryllium outer electrons make "four" 1 × de Broglie wavelength orbits ..
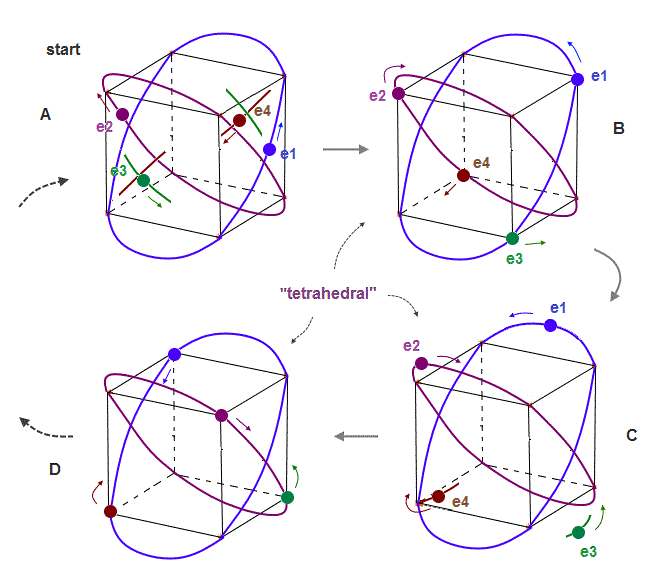
If the number of valence electrons of beryllium is "four", and all these orbits are 1 × de Broglie wavelength, their periodic motions become like Fig.7.
Due to symmetry and Coulomb repulsions among four electrons, "tetrahedral" distributions are formed in this process.
(Fig.8) "e3" electron feels only "opposite" wave phases of "e1" and "e2" !
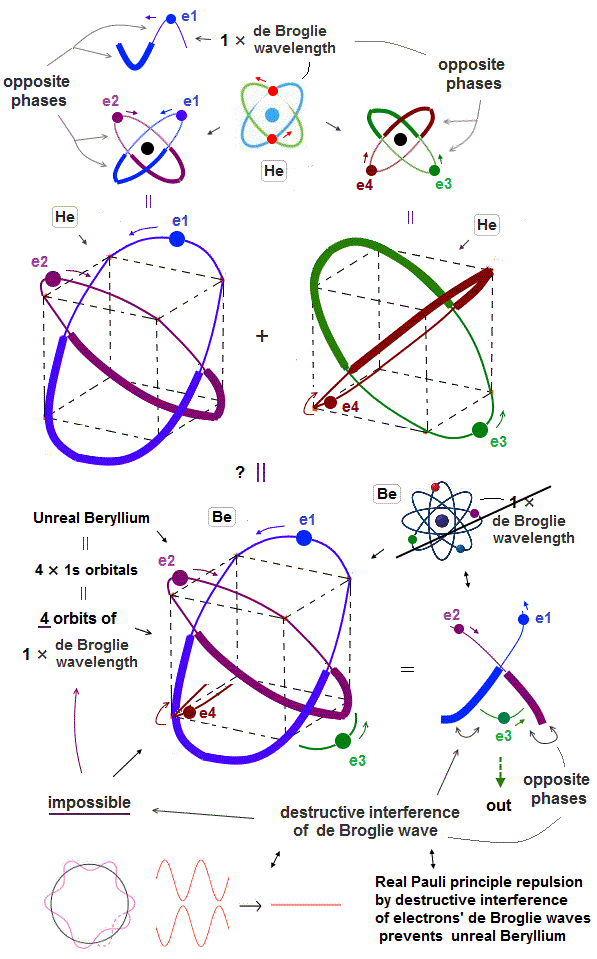
But as shown in Fig.8, when "e1" and "e2" electrons pass the upper part of this atom, the lower part contains only "opposite" wave phases of "e1" and "e2" orbits, because they are 1 × de Broglie wavelength.
So "e3" ( and "e4" ) orbits feel only "opposite" wave phases of "e1" and "e2" orbits and be disturbed and unstable.
(Fig.8') "e3" electron can pass the midpoints between e1 and e2, "safely"in Neon.
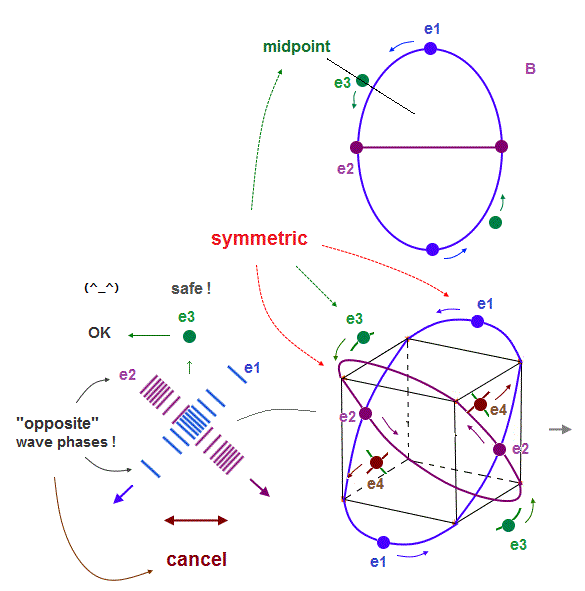
On the other hand, in Neon consisting of four 2 × de Broglie wavelength orbits, each electron can move stably, NOT disturbed by the opposite phases of other orbits.
As shown in Fig.8', "e1" and "e2" orbits are just symmetrical with respect to "e3", when it passes the point which is the same distance from e1 and e2.
The wave phases of "e1" and "e2" are just opposite from each other at this point of "e3".
So their wave phases are cancelled out to be zero, which doesn't disturb "e3" de Broglie waves.
So, different from 1 × de Broglie wavelength, each electron in 2 × de Broglie wavelength orbit can move safely and stably, even when four orbits are included.
(Fig.9) Both Ne and Ar forms stable "hexahedral" structure.

Considering periodic table and sudden drop in the first ionization energy, it is quite natural to think Neon is 2 × de Broglie wavelength, and Argon is 3 × de Broglie wavelength in outer orbits.
Both Ne and Ar contain eight valence electrons, so each orbit contains two electrons in these atoms.
(Fig.10) Orbits of Neon cross each other "perpendicularly".
(Fig.11) Orbits of Neon cross each other "perpendicularly".
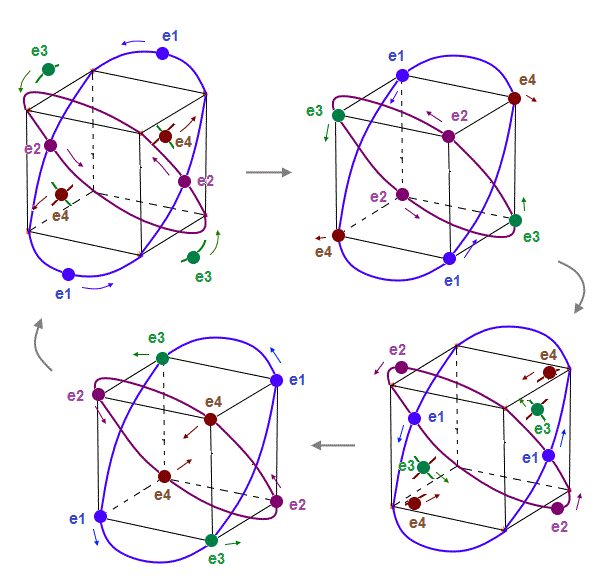
As shown on this page, we can show the appropriate new Neon model, in which orbits can cross each other "perpendicularly". "Perpendicular" crossing means they can avoid "destructive" interference.
(Fig.12) Orbits (= opposite wave phases ) always cross each other "perpendicularly".
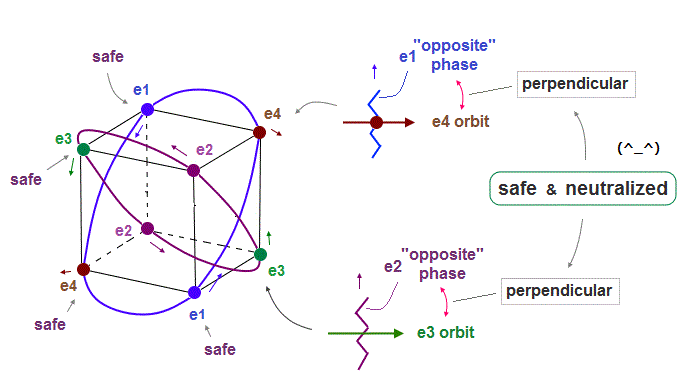
Each electron can cross other electrons' orbits perpendicularly, when they are opposite wave phases to each other, because "perpendicular" crossing avoids destructive interference.
Furthermore. crossing of "opposite" wave phases can neutralize total wave phases at all points.
( Strictly speaking, the positions of these opposite phases are a little different. But almost the same. )
"Neutralization" of wave phases means any other electrons can be free from other wave ( bad ) influences, and move stably and independently, NOT to be disturbed.
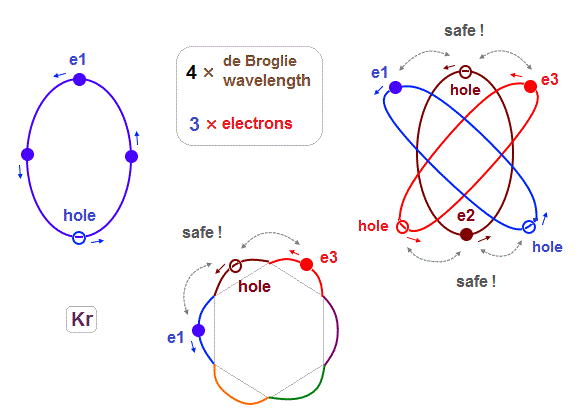
(Fig.13) Each Ar orbit contains two electrons and one hole.
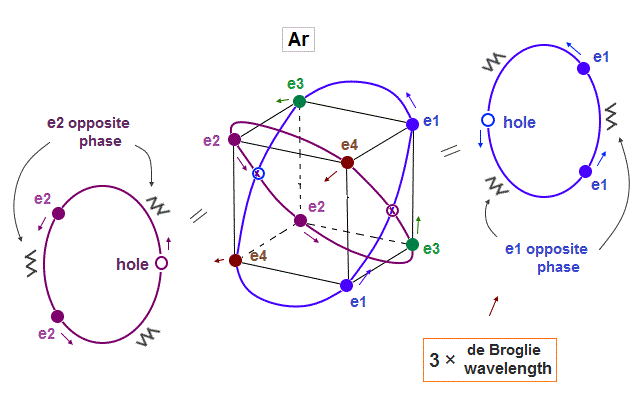
If Argon orbit is 3 × de Broglie wavelength, and each orbit contains two electrons, it must include one "hole". "Hole" is the same phase as the position of each electron, but it doesn't have an electron.
Also in this case of Argon, each two orbits ( ex. "e1" and "e2" ) can cross "perpendicularly", keeping symmetrical distribution.
(Fig.14) Eight valence electrons of Ar can keep stable "hexahedral" structure.
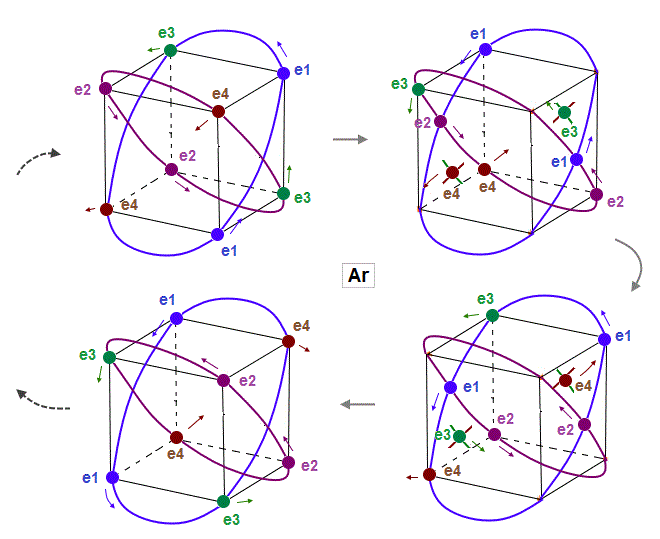
As shown in Fig.14, eight valence electrons of Argon can also move stably and keep symmetrical hexahedral distribution, like Neon, in which the opposite wave phases in two orbits cross perpendicularly.
(Fig.15) When de Broglie wavelengths are different, their orbital sphapes are different.
If Neon and Argon have the same numbers of valence electrons and orbits, their orbital shapes are a little different, because, 3 × wavelength orbit is a little longer.
As shown in Fig.15, the orbit of Argon is closer to "circular" (= wider in width ) than Neon.
( Of course, in these multi-electron atoms, each orbit cannot be genuine circular or elliptical ).
(Fig.16) Ionization energies show us "where" de Broglie wavelengths change.
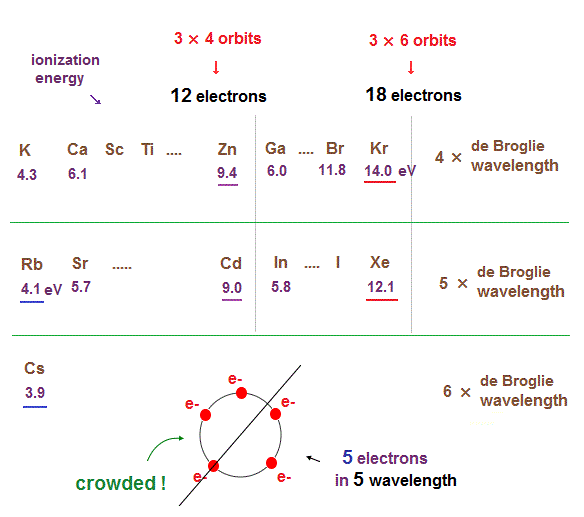
In the same way, sudden drop in inonization energies show us "Kr" and "Xe" are the last atoms in 4 × and 5 × de Broglie wavelength orbits.
As seen in this and this, the changes of ionization energies from "4s" to "3d" orbitals are too smooth, meaning "4s" and "3d" are the same type of orbits. Quantum mechanical orbitals are too artificial.
As de Broglie wavelengths (= orbtial radius ) get bigger, the spaces between each orbits get wider.
So "packing" maximum electrons into one single orbit ( 5 electrons in 5 wavelength orbit ) causes strong repulsive Coulomb forces due to the imbalance in electron's distributions in all space.
In Kr and Xe, we consider each orbit contains 3 electrons and they form three pairs ( each pair is two orbits ), the total becomes 6 orbits ( 3 × 6 = 18 ).
(Fig.17) 6 orbits of Kr outer electrons.
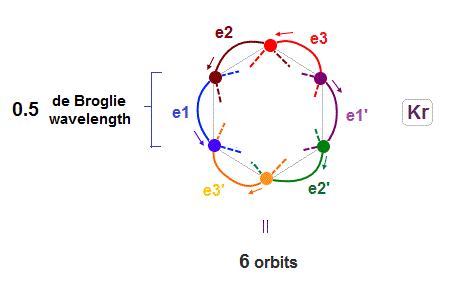
Like Neon (= 4 orbits ), Krypton six orbits generate three pairs, each contains two perpendicular orbits with opposite phases and opposite directions ( e1-e1', e2-e2', e3-e3' ).
Fig.17 is Krypton orbits seen from the upper side.
0.5 × de Broglie wavelength orbit is included between two closest intersections, like Neon and Argon.
(Fig.18) Each orbit of Krypton's outer electrons.
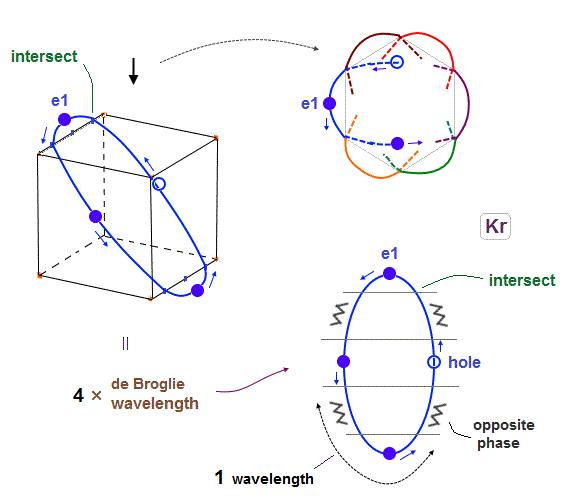
Considering the number of Kryoton valence electrons is "18", each 4 × de Broglie wavelength orbit contains three electrons and one hole (= 3 × 6 = 18 ).
When each orbit comes closer to another orbit, these two orbits tend to be perpendicular to each other.
( As shown in Biot-Savart law, the influence of de Broglie waves gets stronger in inverse proportion to the distance from de Broglie wave. )
(Fig.19) e1 and e1' orbits form a "pair" crossing perpendicularly in opposite phases.
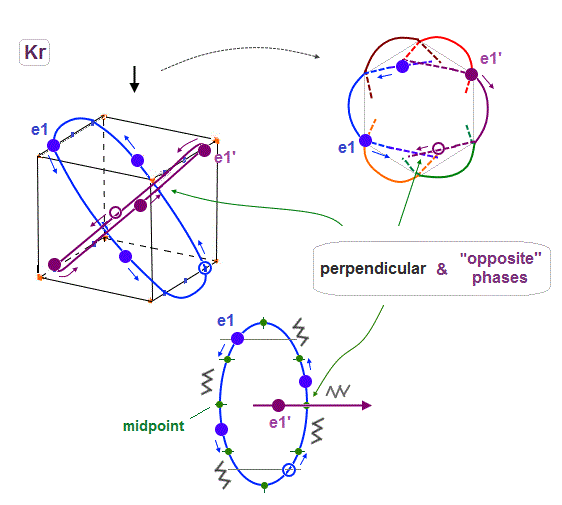
Like Neon and Helium cases, each two orbits form a pair, in which these two orbits cross each other "pependicularly", and at these intersections, their wave phases are just opposite (= ± ) to each other.
As a result, destructive intereference can be avoided, and wave phases at each intersection can be neutralized to be zero.
Basically the points at an equal distance between the two same phases (= + and + ) are just the opposite (= - ). So considering Coulomb repulsion, other electrons tend to cross these opposite-phase points.
(Fig.20) e1 and e2 orbits also cross perpendicularly in the "opposite" phases.
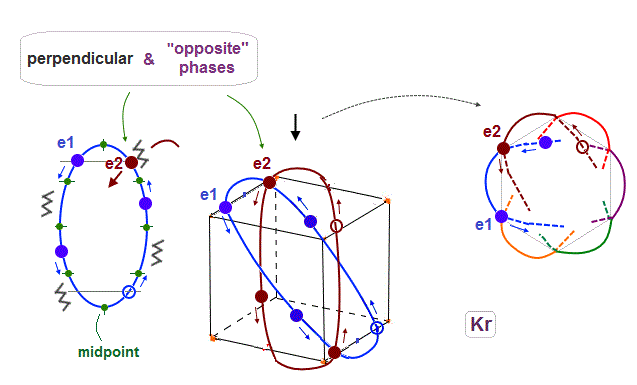
As shown in Fig.17, when 0.5 de Broglie wavelength is included between two intersections, e1 and e2 ( next to e1 ) orbits with the "opposite" phases can also cross perpendicularly.
(Fig.21) 4 × de Broglie wavelength orbits allow this crossing, too. ↓
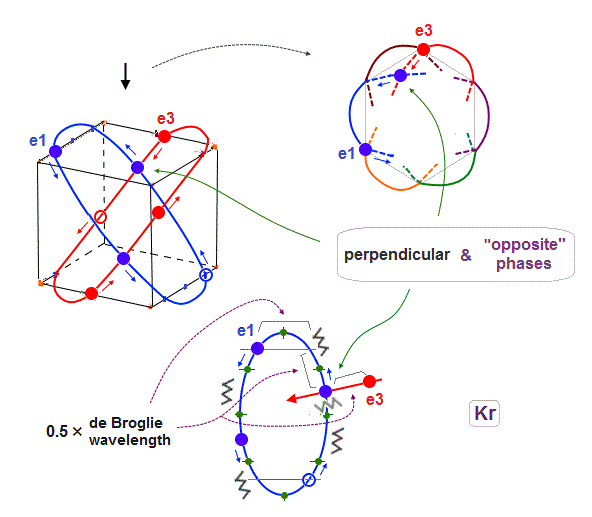
When each orbit is 4 ( or 5 ) × de Broglie wavelength, it includes enough wave "crest" and "trough" to make orbits next to the next (= e1 and e3 ) cross perpendicularly in the state of the opposite wave phases to each other.
As a result, e1 orbits can cross all other orbits ( e2, e3 and e1' - e3' ) perpendicularly in the states of the "opposite" wave phases to each other, when each orbit is 4 ( NOT 2 ! ) × de Broglie wavelength.
(Fig.22) e1 and e1' cross perpendicularly + 4 × midpont lines = total 6 orbits !
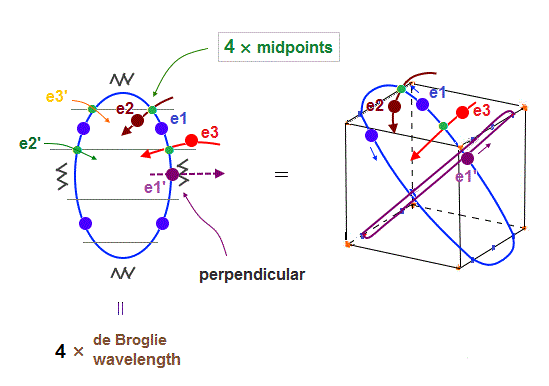
As shown in Fig.22, when e1 and e1' orbits cross perpendicularly, e2 and e3 orbits are just on the different midpoint lines (= zero phase ).
e2 and e3 have their own "symmetrical" partner orbits, e2' and e3', so the total is four midpoint lines are necessary in 6 orbits. Because "perpendicular" e1 and e1' (= 2 ) + 4 midpoint lines become "6" orbits.
(Fig.23) "e3" and "e1" orbits crash into each other in 2 × de Broglie wavelength.
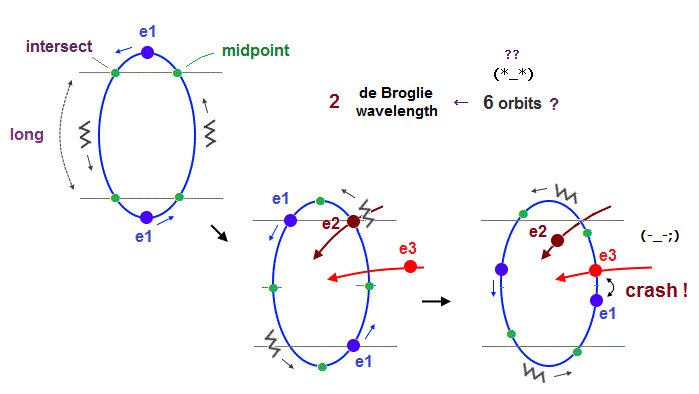
If we try to make 6 orbits using 2 × de Broglie wavelength orbits like Neon, we will find this is impossible, because the number of wave "crest" and "trough" is too small to harmonize all 6 orbital phases with each other.
First, if we try to do this, each orbital shape becomes "unsymmetrical" ( half wave phase is short, and another half is long, as shown in Fig.23 ).
When we suppose "e1" and "e2" (= next to e1 ) cross perpendicularly in the opposite phases, e1 and e3 (= next to the next ) electrons crash into each other !
Like Krypton, when each orbit crosses all other 5 orbits in the opposite wave phases safely (= avoid two electrons' crash, see Fig.19-21 ), their de Broglie wavelength must be 4 ( or 5 ), when six orbits are included.
(Fig.24) To harmonize with all other orbits, 4 × de Broglie wavelength is indispensable.
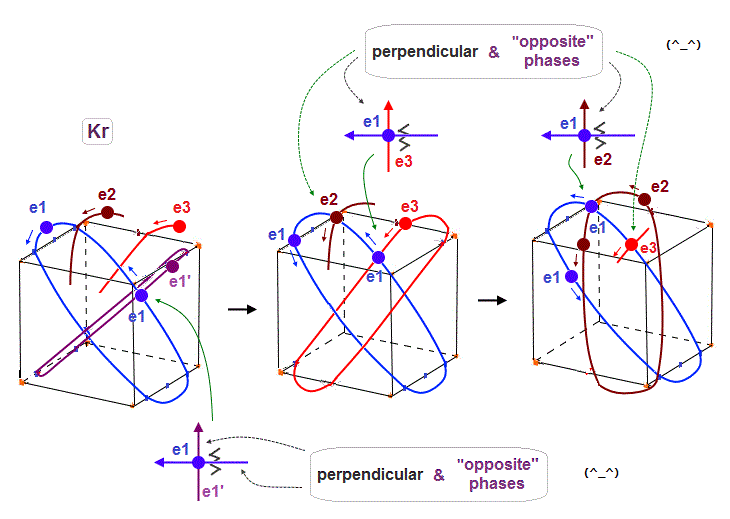
As shown in Krypton, when each orbit is 4 × de Broglie wavelength, each orbit can cross any other orbits in the opposite wave phases (= two same-phase electrons don't crash ), harmonizing with each other.
In Fig.24 left, e1 crosses e1' orbit perpendicularly in the "opposite" phases.
In Fig.24 middle, e1 crosses e3 orbit perpendicularly in the "opposite" phases.
In Fig.24 right, e1 crosses e2 orbit perpendicularly in the "opposite" phases.
In case of 2 × wavelength like Neon, the number of wave "nodes" is too small to harmonize with all other 5 orbits in wave phases, which causes "crash" between two electrons somewhere.
(Fig.25) To avoid strong Coulomb repulsion, "one hole" is necessary.
Different from Neon and Argon case (= 8 electrons, hexahedron ), when the total number of outer electrons is "18", they cannot form regular polyhedron, so some imbalance is seen in their electrons' distiribtion.
For example, as shown in Fig.25, three electrons e1-e3 come closer to each other in the upper part of Krypton atom. In this state, "e2" electron has to enter between "e1" and "e3" in spite of their stronger Coulomb repulsions.
(Fig.26) When 4 × de Broglie wavelength orbit contains only "3" electrons (= 1 hole )
If each 4 × de Broglie wavelength orbit contains only 3 electrons ( meaning the left one is empty "hole" ), these Coulomb repulsions can be alleviated.
For example, In Fig.26, "e2" electron can avoid entering the point between "e1" and "e3", thanks to its empty "hole". Alleviation of Coulomb repulsions happens alternately in different positions.
But if 4 × de Broglie wavelength orbits contains only 2 electrons (+ 2 holes ), its electron's number is too small to maintain this electrons' distribution and structure consisting of "6" orbits.
(Fig.27) Xenon's orbit is longer than Krypton, so its shape gets "wider".
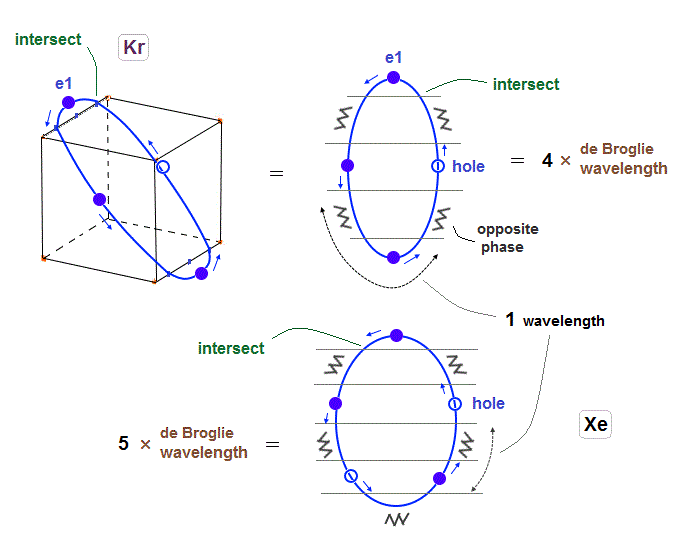
As I said in Fig.2 and Fig.16, Xenon orbit is 5 × de Broglie wavelength.
So the total orbital number of Xenons becomes "6" like Krypton, because the odd "7" orbits cannot form symmetrical "pairs"
(Fig.28) "e1" electron of Xenon crosses e1', e3 and e2 orbits in the "opposite" phases, safely.
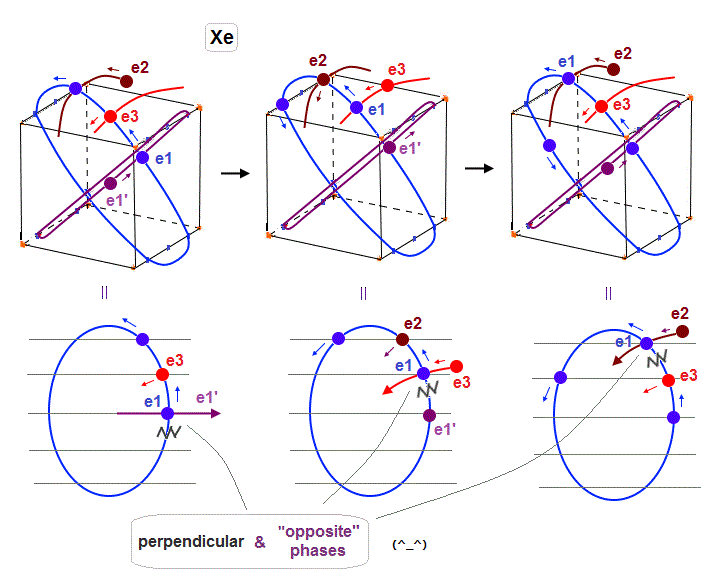
As shown in Fig.28, also when each orbit is 5 × de Broglie wavelength, its number of wave "crest" and "trough" is enough to make all six orbits "harmonize" and cross each other in the "opposite" phases.
In Fig.28 left, e1 crosses e1' orbit perpendicularly in the "opposite" phases.
In Fig.28 middle, e1 crosses e3 orbit perpendicularly in the "opposite" phases.
In Fig.28 right, e1 crosses e2 orbit perpendicularly in the "opposite" phases.
(Fig.29)
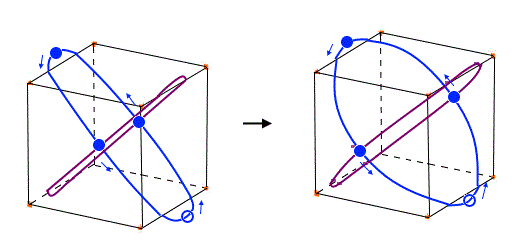
Xenon's orbit is longer than Krypton, so the width of Xenon's orbit becomes wider than Krypton.
In any cases, 0.5 de Broglie wavelength is kept between two intersections.
(Fig.30) Each orbit cannot be in "one plane" in multi-electrons.
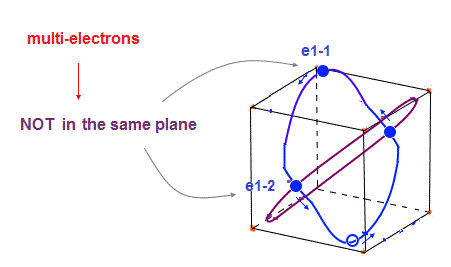
In these multi-electron atoms, each orbit cannot be in the same one plane like one-electron hydrogen.
So each orbital shape becomes more complicated, obeying the total effects of de Broglie waves ( ex perpendicular ) and Coulomb forces.
Of course, all six orbits must be symmetrical to each other in noble gases.
(Fig.31) The total number of valence electrons of Rn is 32 (= 4 electrons × 8 orbits ).
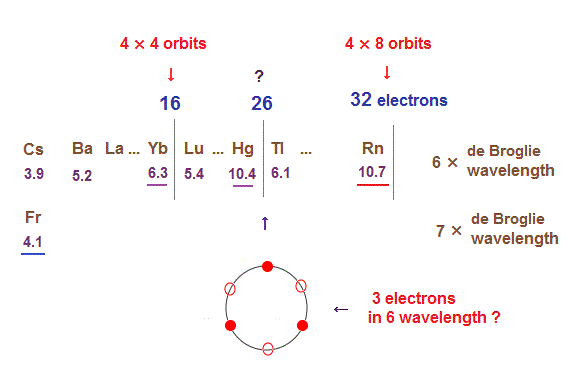
As de Broglie wavelengths increases, the midpoint lines (= zero phase ) increases in number, meaning they can contain more orbits stably.
In 6 × de Broglie wavelength orbit of Radon (= Rn ), the total 8 orbits can be included due to increased midpoints. So 4 electrons ( in each orbit ) × 8 orbits become 32 electrons in Rn atom.
(Fig.32) Each Rn orbit contains 4 electrons and 2 holes.
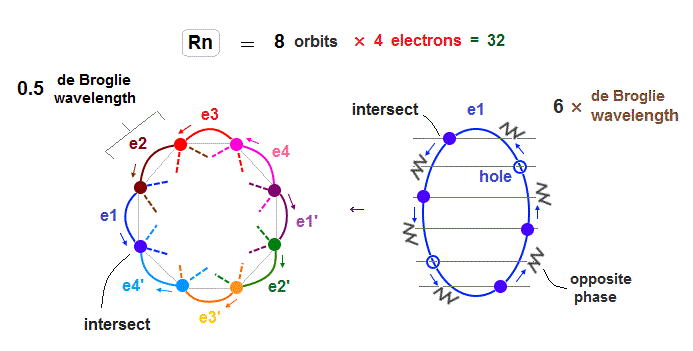
As I said in this section, as the number of electrons in one orbit becomes larger, imbalance in electron's distribution in all space becomes greater.
So in Radon case, we can think each orbit contains only 4 electrons ( + 2 holes ) to avoid stronger Coulomb repulsions and imbalance in its distribution.
Like Krypton case, each two orbits form a "pair", crossing perpendicularly and safely in the opposite wave phases.
e1-e4 ( or e1' - e4' ) electrons are moving in the same directions.
(Fig.33) Radon outer electron's motion (= 6 × de Broglie wavelength ).
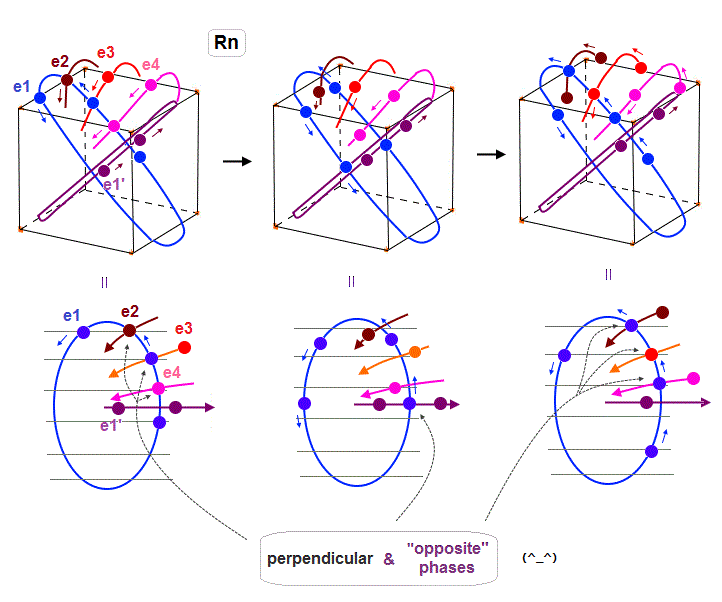
Radon is 6 × de Broglie wavelength, so each orbit includes enough wave "crest" and "trough" to make all 8 orbits "harmonize" and cross each other in just the opposite phases.
In Fig.33 left, e1 ( e2, e4 ) crosses e3 ( e1, e1 ) orbit perpendicularly in the "opposite" phases.
In Fig.33 middle, e1 crosses e1' orbit perpendicularly in the "opposite" phases.
In Fig.33 right, e1 ( e3 ) crosses e2 ( e1 ) orbit perpendicularly in the "opposite" phases.
As a result, we can prove de Broglie wavelength determines the maximum orbital number (= Pauli exclusion principle ), NOT depending on unrealistic spin, which magnetic moment is too weak to influence them.
In small atoms such as Helium and Neon, each electron can move independently in respect of electron's moving speed. But in large atoms such as Kr, Xe, Rn, their speed in the same orbit must be equalized.
Besically the potential energies of all electrons tend to be equal to each other, so all electrons' speed tend to be equal, too. When there are a little difference in their potential energies in the same orbit, it is thought faster electrons "push" slower electrons, equalizing their speed.
As shown in Compton effect, each de Broglie wave can exert some "forces", because they have "momentum"

2015/5/3 updated. Feel free to link to this site.