トップページ
スピンは ない。
人為的なスピン。
スピンホール効果
レア・アースの "スピン" ?
1重項、3重項は まったくスピンと無関係。
微細構造=スピン軌道は 間違い。 (14/8/17)
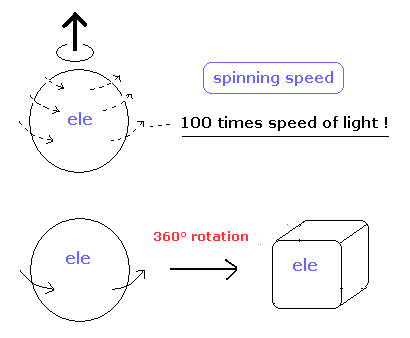
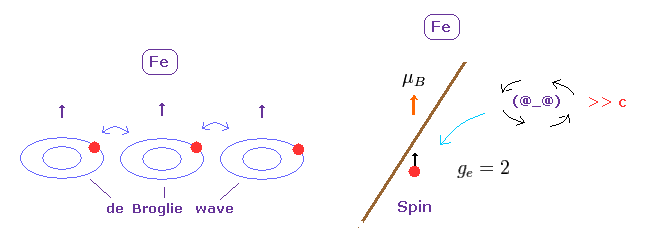
(Fig.1) 電子スピンは どんな風に スピンするの ?

"スピン" は 現在の量子論において 最も重要で基本的な概念の 1つである。
"スピン" は パウリの排他原理、量子もつれ、フェルミ統計、素粒子理論、超弦理論 にとって 必要不可欠である。
しかし、奇妙なことは、もし あなたがたが これらの専門分野の人達に "スピン" とは どんな姿形をしているのか 質問したとしても、彼らは まったく具体的な解答を与えることができないだろう。
量子力学と "スピン" が 誕生してから かれこれ 100 年近くも経つのに 奇妙としか言いようがない。
この理由は このページ に示したように、 "スピン" は 実在の物で 説明 できないからである。
スピン 1/2 粒子を 360°回転しても 元の状態に戻れない。
単一電子は 非常に軽い点状粒子のため、そのスピン速度は 光速をはるかに越えなければならない。
(Fig.2) 点状粒子 → スピン速度は 光速をはるかに超える。
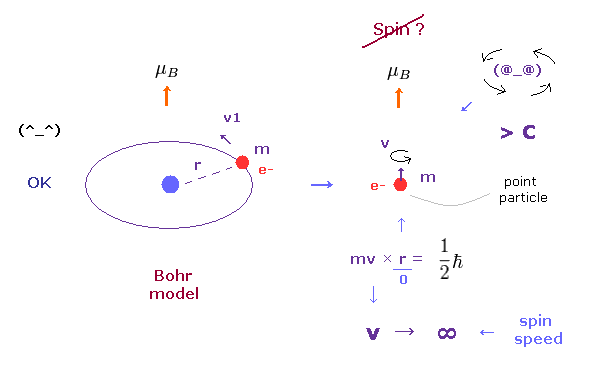
水素原子の 基底状態では 電子の磁気モーメントは ボーア磁子 (= μB ) の大きさである。
ボーア模型では この磁気モーメントは 電子が 円軌道上を運動することによって生じる。
しかし 量子力学は 角運動量 がゼロ ( L = 0 ) のため、
この 磁気モーメント μB は "スピン" によって生じることになっている。( このページも参照のこと。 )
Fig.2 を見てお分かりのとおり、 点状粒子の電子が 角運動量 1/2 ħ を引き起こすことは 不可能である。
角運動量は mv×r で与えられ、その半径 "r" は 点状粒子では ほぼゼロである。
結果的に、回転スピード "v" は 1/2 ħ に達するのに 光速より はるかに 速くなる必要がある。
(Fig.2') 陽子のスピンは 大丈夫。 電子スピンは存在しない。

一方で、一定の大きさのある重い陽子は 光速を越えることなく "本当の" スピン回転をすることができる。
つまり 原子核のスピンは リアルであり、電子スピンは 実在しないということになる。それは ボーア模型のように スピンでなく 単に 円軌道上の運動であることを示している。
実際、電子スピンの磁気モーメントは 陽子の磁気モーメントの 1000 倍以上もの強さがある。同じスピン、電荷なのに違いすぎである。
この 極端な相違は 電子スピンが ある大きさの半径の円軌道運動によって生じ、自身の自転によるものでないことの証しである。
このページも参照のこと。
(Fig.3) スピンは 本当に強磁性やパウリの排他律を引き起こせる ?
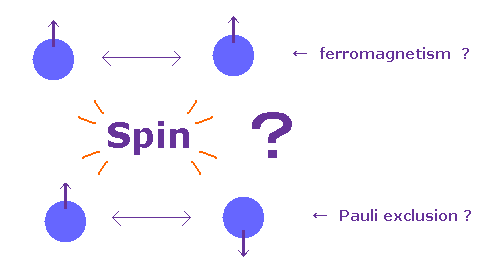
教科書では 強磁性体において 原子の各スピンは 互いに平行になろうとすると書いてある。
また パウリの排他原理では 3番目のスピン電子が すでに up と down スピン電子のある同一軌道上には 入れないことになっている。
これはつまり、スピン磁気モーメント (= up もしくは down ) には これら反発相互作用を引き起こせるだけの 十分な パワーがあるということだろうか?
実は スピン磁気モーメントは 強磁性やパウリの排他原理を引き起こすには 余りにも弱すぎるのである。
なぜなら スピン・スピン相互作用の大きさは 微細構造レベル (= 1.0 × 10-5 eV ) と同じぐらいしかないからである。
(Fig.4) パウリの排他原理の反発力は かなり強い (= リチウムで 約 11 eV ).

リチウムの 3番目の電子は 2s 軌道にあるが、もし リチウムの3つすべての電子が 2s よりも はるかに原子核に近い 1s 軌道に存在すると、基底状態のエネルギーが -214.3 eV 未満になり、これは 実験値 -203.5 eV よりも低くなってしまう。( Quantum chemistry 6th, Ira N. Levine, p 292 )
つまり、実験値に合うには 3つ目の電子が 原子核の 強いクーロン引力に打ち勝って 1s から 2s に押し出す反発力が必要になる。この大きさは 上記の差で 約 11 eV ぐらいになる。
(Fig.5) スピン・スピン相互作用は 弱すぎる。

パウリの排他原理では 互いのスピンの向きの関係で その軌道に入れるかどうかが決まるため、あたかもスピン磁気モーメントの相互作用が この 11 eV の反発力の源のように錯覚しやすい。
しかし 計算してもらうとわかるが この 磁気双極子相互作用というのは 微細構造ぐらい ( 1 × 10-5 eV ) の大きさぐらいしかなく、 とてもじゃないが クーロン力に対抗できるものではない。
つまり このパウリの排他原理の強力な反発力を説明するには 別の何かの力を借りなければならない。
スピン磁気モーメントが弱すぎて役に立たないとすれば 残りは1つしかない。
このページに示したように ドブロイ波の干渉作用が パウリの反発力の原動力と考えると しっくりくる。
(Fig.6) 強磁性の起源 = スピン ?
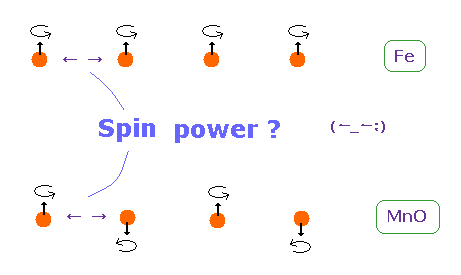
強磁性では、鉄などの 各スピンが 互いに平行に揃うことによって生じるとされている。
一方、 MnO などの 反強磁性では 各スピンが 互いに 反平行になるように相互作用するとしている。
ということは、(反)強磁性の 起源 は 多くの教科書が言うように "スピン" ということになるのだろうか?
実は、スピン磁気モーメント間の相互作用というのは 強磁性などを引き起こすには、
これもまた 余りにも弱すぎるのである。
(Fig.7) 強磁性の起源 = 交換相互作用 "J" ?

現在の量子論では (反)強磁性の力を ハイゼンベルク模型の 結合定数 (= J ) で 表そうとしている。
この交換相互作用を表す結合定数は 1 eV ぐらいの大きさがあり、スピン・スピン磁気相互作用 (= 10-5 eV ) に比べて はるかに大きい。
つまり スピン磁気モーメントによる 相互作用は こういった磁性体を説明するには
桁が 小さすぎなのである。 (
このサイト や
このサイト も参照のこと。)
スピン磁気相互作用は 温度表示で 0.3 K しかなく、これは 室温の熱雑音で 容易に 壊れてしまう。
( 例えば、鉄は 1043 K ほどでも強磁性体になることができ、この温度は 0.3 K よりもはるかに大きい。 )
(Fig.8) ドブロイ波の相互作用が 強磁性の起源である。
スピン・スピン磁気相互作用は 磁化を説明するには 非現実的なくらい 弱い。
ここでも 1つしか残っていない。
電子の軌道運動は ドブロイ波を伴う。 ( このページを参照のこと。 )
強いパウリの排他原理の反発力のように、これらの同調するドブロイ波が 強磁性を 室温で
安定 にさせていると考えるのが自然である。
ダビッソン・ガーマーの干渉実験に見られるように、ドブロイ波の干渉作用は クーロン力による散乱方向を変えるだけの力がある。
(Fig.9) 1重項、3重項は 単なる "数式" 記号にすぎない。
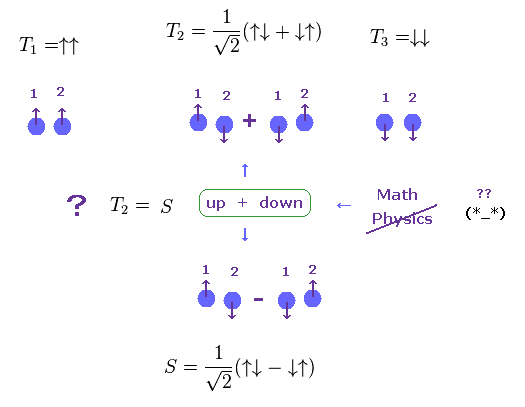
現在の量子力学では、"スピン" が 1重項、3重項の起源とされている。
しかし実は、これら 1重項、3重項のエネルギー差は クーロン相互作用ほどの強さがあり、 スピン磁気モーメントでは 説明できないのである。 ( Fig.10 参照のこと。 )
さらに、これらの 1重項、3重項は 現実の物では 表せない。
3重項の T2 と 1重項 (=S ) の両方において、2つの電子は 1つが "up" 方向のスピン、もう1つが "down" 方向のスピンを持つ。
つまり これらの T2 と S は 共に up + down 状態で まったく同じエネルギー状態で 区別がつかない ということになってしまう。
しかし 彼らによれば、実態のない数式記号 (= ± ) により、これらの状態は 立派に別のものだということになっているのである。
スピン状態を意味する この奇妙な数式記号 (= ± ) を 現実の物を使って 思い浮かべられる 人は 果たして いるだろうか?
現実的な視点からすれば、これら 1重項、3重項は 多電子原子における 電子間クーロン相互作用か何かに基づくということは明白である。
(Fig.10) 1重項、3重項は クーロン相互作用ぐらい強い。
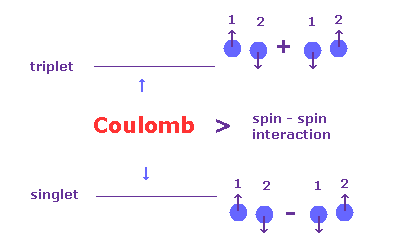
朝永振一郎の ”スピンはめぐる” には、1重項、3重項は スピン・スピン相互作用では 説明できない ことが書かれてある。
----------------------------------
[ p.94 ] 当然 2個の電子のスピンは 磁気的な作用を及ぼし合うでしょうが、実験を見ると それより 4〜5桁ほど大きいスピン同士の相互作用があるように見える。
[ p.99 ] ところで、スピン同士の相互作用エネルギー Es,s は どの程度の大きさを もつのでしょうか。-- 図6の1重項の準位と 3重項の準位 をくらべればよい。--- そうすると、スピン同士の相互作用は 相当大きいことがわかる。
[ p.100 ] しかしながら、こういう磁気的起源のエネルギーですと E (n,l:0) と E (n,l;1) との間隔は、せいぜいアルカリ2重項 (= 微細構造 ) の準位間隔ぐらいにしかならない。ところが 図6を見てもわかるように、それは電気的起源のものぐらい大きい。このことが長い間の謎だったのである。
-------------------------------------
3重項は まったく スピン と無関係 のページも参照のこと。
(Fig.11) 水素原子の異常ゼーマン効果? ↓ = ボーア・ゾンマーフェルト模型。

水素原子のスペクトラム線は ナトリウムやカリウムなどの 他のアルカリ金属よりも
はるかに少ないことが知られている。
電子の "スピン" を仮定したら、水素原子のエネルギー準位は はるかにもっとたくさんに 分裂しなければならない。
そのため、彼らは解釈を都合よく変更して、水素原子では 様々な異なるエネルギー準位同士 ( 2s1/2 = 1p1/2 ... ) が 偶然に 一致していると 言いだした。 このページを参照のこと。
正常ゼーマン効果によれば、各 "n" のエネルギー準位は 1重項 ( 2重項でなく ) であり、磁場のもとで、 3つに分離するとされている。
多くのウェブサイトや教科書では 水素原子も 異常ゼーマン効果を示すとしている。
しかし 実は この水素の異常ゼーマン効果は ゾンマーフェルトの 微細構造 で説明可能なのである。
水素原子では、微細構造の2重項の各線が それぞれ ( 正常ゼーマン効果にあたる ) 3分裂をする。 ( 結果、2 × 3 = 6 ).
(Fig.12) J Mehra's のテキスト。

量子力学の誕生に至る歴史を語った本、 Historical Development of Quantum Theory v.1 part2 ( J. Mehra ) の 659 ページには次のように書いてある。
--------------------------------
1922 年、 Otto Oldenberg は 次のような結果を得た。
弱い磁場のもとでは、バルマー系列の Hα の 2重項の各ラインが 正常ゼーマン効果の 3つの準位に分離し、 強い磁場のもとでは、 2重項のゼーマンパターンが 1重項のゼーマンパターンに変化した。
---------------------------------
つまり、水素原子における これら2重項を "異常ゼーマン効果" と 呼んでいるだけなのである。
もうご存じのとおり、これら2重項 (= 微細構造 ) は 奇妙な "スピン" に頼らずとも、ボーア・ゾンマーフェルト模型で 完全に 説明可能なのである。
(Fig.13) ゼーマン効果の歴史。

上記のテキストによれば、異常ゼーマン効果は Na, Cd, Mg などの 多電子原子に 主として見られたと書いてある。
水銀 (= Hg ) では 1898 年に 磁場のもとで 11 ラインもに分離するのが確認された。
重要な点は 異常ゼーマン効果について語るとき、基本的に 水素原子には まず 触れない ということである。 ( Fig.11 は 唯一の例外 である。 )
また この本は ほとんどの多電子原子 ( H, He, Li などの軽い原子を除いた ) では 単純な 2重項、3重項よりも はるかに複雑な 分離線が観察されるとしている。
そのため 当時、ハイゼンベルグや ランデは 異常ゼーマン効果は スピンでなく内殻の電子群によって生じると 最初 考えていたぐらいである。
また 様々な原子や金属は ランデのg因子に 従わないのである。
この事実が ラッセルやサンダーズに jj, jk カップリングなどの 新たな概念を創出させる動機となった。
(Fig.14) 正常ゼーマン。

多くの教科書では、リチウムやヘリウムなどの軽い原子は 異常ゼーマン効果を語るとき 通常 触れられない。
上記の本の 450 ページ目には、" リチウムの赤線は それ以上 分離せず、正常な 3つの分離線が観察され、彼らを驚かせた。”と書かれている。
なぜなら リチウムは ナトリウムやカリウムと 明らかに 異なっていたからである。
この奇妙な食い違いを説明するために、後に 彼らは リチウムは パッシェン・バック効果 (= 正常ゼーマン効果に似る ) を示しているという解釈を提案した。
しかし 原子の電子数の増加に従い、より多くの分離線が 観察されるという事実から、異常ゼーマン効果は "スピン" でなく 他の電子間との相互作用で生じると考えるのが ごく自然である。
(Fig.15) 量子力学によれば、スピンの大きさは "1/2" ではない?
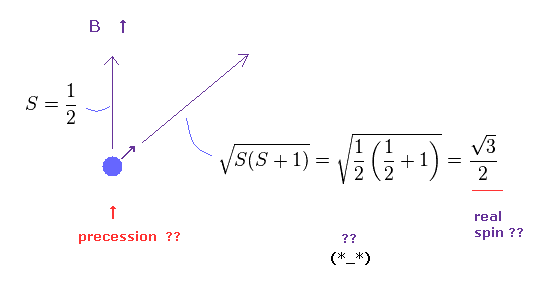
磁場の下では、スピン磁気モーメントの大きさは ボーア磁子の大きさになる。
つまり 磁場 (= B ) の方向の スピン角運動量は S = ± 1/2 に量子化されていることになる。
奇妙なことに、量子力学によれば、Fig.15 に示したように、 真のスピン角運動量は 1/2 よりも 大きいことになっている。
角運動量の 本当の大きさは スピンの歳差運動によって S(S+1) の平方根で表されると 彼らは主張している。
(Fig.16) スピン + スピン ?
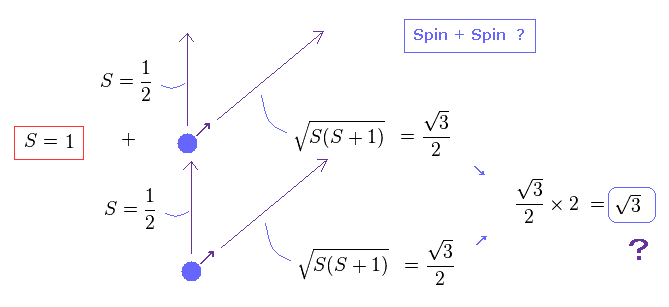
問題は 多電子原子での 複数のスピン効果を合計するときに 起きる。
彼らは 単純に 外殻電子のスピンの和を トータルのスピン効果と見なしている。
つまり 2つの電子が存在するとき、磁場方向の トータルのスピンは
1/2 + 1/2 = 1 になる。
結果的に 歳差運動方向の トータルのスピンの本当の大きさは Fig.16 に示したように、 3 の平方根 になるのだろうか?
(Fig.17) スピン + スピン ← 自己矛盾。
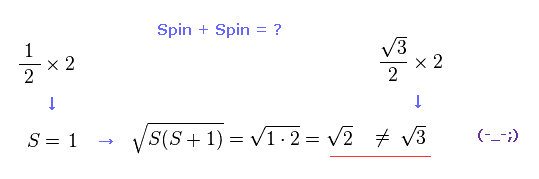
しかし S = 1 を S(S+1) の平方根に代入すると、この計算結果は 2 の平方根 ( 3 ではなく ) になってしまう。
これは 明らかに自己矛盾である。
つまり 2つの電子が 2つの ( 異なる ) 外殻軌道に存在するとき、それらは うまい具合に 互いに微調整し合って 全スピンが ちょうど 2 の平方根にならなければならない。はっきり言って できすぎである。
ご覧の通り、これらの量子力学のスピンにまつわる解釈は 余りにも不自然で 非現実的な産物なのである。
(Fig.18) ランデのg因子は 正しいのか ?
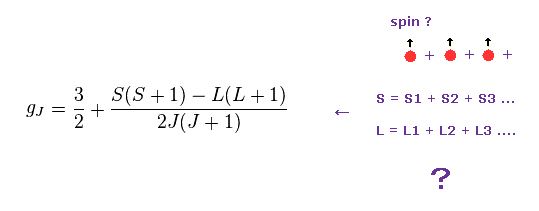
このページに示したように、ランデのg因子は 非常に不自然な 歳差運動に基づいている。
多電子原子では、Fig.18 のように 各スピンを合計している。
結果的に、Fig.16 や Fig.17 の 自己矛盾 が起きてしまう。
(Fig.19) 磁場 H 方向に観測される磁気モーメント。
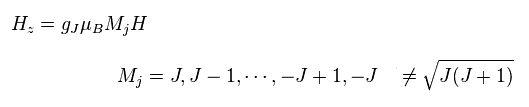
Fig.18 の ランデのg因子を用いて、磁場方向 H に観測される 原子の磁気モーメントのハミルトニアンは Fig.19 のようになる。
重要な点は z 方向の量子数 (= Mj ) は 整数値であって、 J(J+1) の平方根ではないということである。
(Fig.20) 磁場 H 方向に観測される 磁気モーメント。
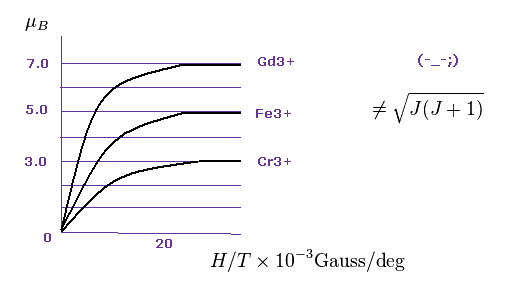
Gd2+, Fe3+、 Cr3+ などの 金属イオンの 磁気モーメントは 例えば この論文 ( W.E. Henry, Phys. Rev. 88 559, 1952 ) に載っている。
Fig.20 に示したように 各飽和磁化は ボーア磁子 (= μB ) の整数倍になる。
ガドリニウムイオンは 7.0 × μB。
鉄イオンは 5.0 × μB。
クロムイオンは 3.0 × μB。
また 酸素分子は 2.0 × μB ( P.Curie, 1895 ) になる。
つまり ボーア・ゾンマーフェルトの 量子化のルールが これらの原子で成り立っていることを示している。
(Fig.21)
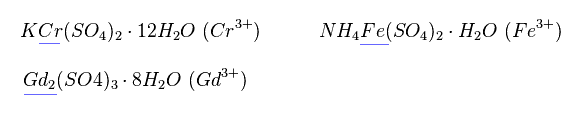
これらのイオンの磁気モーメントは 個別状態では 測定できない。
Fig.21 のような 化合物 の形で測定している。
つまり 周囲の原子の影響が強ければ、当然 磁気モーメントも 単純ではなくなる。
実際に Fe, Cr, Gd などの 中性の金属では 単純な ランデのg因子が 成りたたない。
他の原子の効果が強いせいだと 彼らは主張している。
(Fig.22)
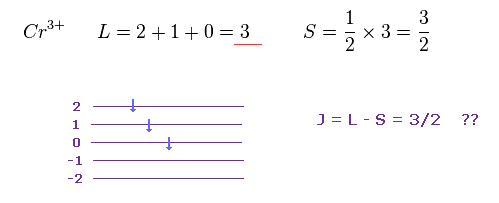
Cr3+ は 3d 軌道に2つの電子を持つ。
フントの法則によれば、 全角運動量 L と スピン S は Cr3+ で それぞれ "3" と "3/2" になる。
上で述べたように、非常に弱い スピン磁気モーメントには それらを 常に平行に揃えるだけの力はない。
Fig.22 の考え方は 余りにも単純で できすぎだと思われないだろうか?
(Fig.23) Cr3+ イオンは ランデの g 因子に従わない。
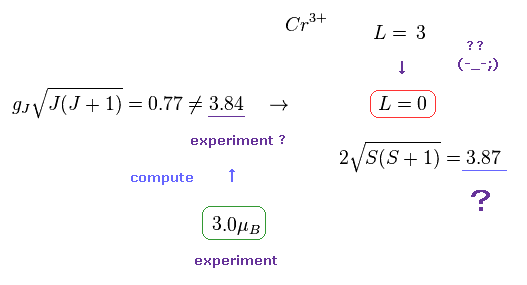
実は Ti3+, V3+, Cr3+, Fe2+, Co2+, Ni2+, Cu2+ などの 遷移金属イオンは ランデのg因子に 従わ ないのである。
奇妙なことに、これらのイオンの全角運動量 (= L ) は 完全に ゼロになると 彼らは主張している。
フントの規則によれば、Cr3+ の角運動量は L = "3" になるのだが、彼らによれば 周囲の原子の影響によって この L が "0" になってしまうとしている。
非常に 都合のいい強引な解釈だと思われないだろうか?
ほとんどの教科書では、J(J+1) の平方根で表される 有効ボーア磁子数 なるものが記載されている。
しかし Fig.20 で述べたように、これら J(J+1) や S(S+1) というのは 実際に 直接 観測できるものではない。
実験から得た 整数値をもとに、各有効磁子数において 平方根を計算しているだけである。
つまり 実験では これらの遷移金属イオンは ボーア磁子の 整数倍 として観察される。
(Fig.24) Gd3+ イオン も ボーア磁子の 整数倍として観察される。
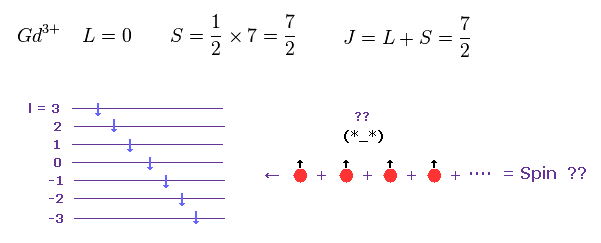
フントの規則によれば、Gd3+ の全角運動量とスピンは Fig.24 のようになる。
各スピンは 異なった軌道に属している。
つまり "7つ" のスピンの合計が 各軌道が 離れているのにも関わらず ちょうど S = 7/2 になるのは
不自然である。
(Fig.25) Gd3+ イオンも ボーア磁子の整数倍を示す。
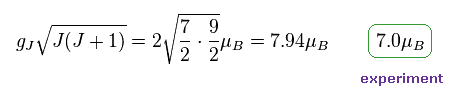
ほとんどの教科書では、Gd3+ の 有効ボーア磁子数は "7.94" と書かれている。
しかし Fig.20 に述べたように、観測される磁子数は Gd3+ でも ボーア磁子の
整数倍になる。
つまり 7.0 の値から 計算で 7.94 を出しているだけなのである。
J(J+1) の平方根自体は 非現実的な "歳差運動" で 直接 観測できるものではない。
このページも参照のこと。
(Fig.26) "スピン" は 単なる 数式記号?

Fig.26 は ハイゼンベルクのスピン模型で 現在の 物性物理学の分野では 頻繁に 使用される。
しかし この模型は 様々な 複雑 かつ ダイナミックに富む 具体的な物理現象を記述するには
抽象的すぎて どう転んでも無理がある。
J が 負 か 正 かに応じて この原子は 強磁性体 か 反強磁性体になると 彼らは主張している。
あなたがたも 感じられたように、様々な原子における 電子の複雑な運動を たった J, S, S の 3種類の記号のみで表せるわけがない。
現在の物理は "スピン" や "パウリの排他原理" とは何かを問うことを 永遠に諦めてしまった。
そのため 非常に 抽象的な数式記号に 頼るしかないのが現状である。
パラメーター "J" は 実験から決めるしか方法がなく 理論そのものだけから 正確に導くことは 不可能である。
つまり この模型では 実験値を再現できるように 調節しているだけにすぎない。
(Fig.27) XY 模型 ?
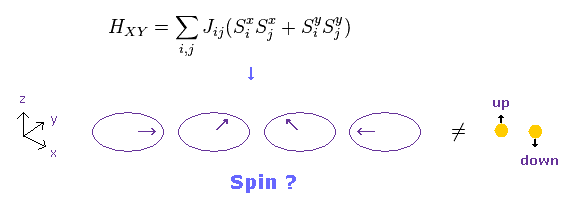
便利なことに、彼らは "XY" モデルというものも導入して、このモデル金属では、何と スピンが x もしくは y 方向へ向くことができるのである。
もし "x" と "y" 方向のスピンが認められると スピンという概念自体も疑わしくなる。
なぜなら この XY 模型は 平行、反平行のスピンの規則に 完全に
矛盾しているからである。
スピンが x 方向も許されれば、 "up"、 "down"、 "水平方向" の 3つの異なるスピン状態があることになる。
結果 最大 3つの電子が 同一軌道に入ることができ、パウリの排他原理が 破綻してしまうことになる。
奇妙としか言いようがない。
(Fig.28) XXZ 模型 ?
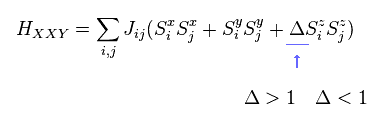
さらに、 XXZ 模型では、各スピンは 様々な方向 (= x, y, z ) を 自由に向くことができる。
J や Δ などのパラメーターは 実験から決めるしかない。
なぜなら 各金属は ほぼ無限の原子を含んでいるため、量子化学によって すべての効果を計算することは 不可能だからである。
物性物理や バンド計算では 密度汎関数法 (DFT) が よく使用される。
なぜなら DFT は それほど時間が かからない手法だからである。
その代り、DFT は 局所密度近似や 様々な 擬ポテンシャルなどの
人為的な近似に頼らなければならない。
つまり これらの DFT の手法は 第一原理とは まったく異なるものなのである。
それにも関わらず 彼らは ”第一原理 密度汎関数法”などの名称をつけたがるが、まったく誤解を与える以外何物でもない。
(Fig.29) ↓ スピン・軌道相互作用。

各金属は 様々な原子を含んでいるため、何らかの近似や 実験結果に頼らずに スピン・軌道相互作用を導くことは 不可能である。
Fig.29 の λ は スピン・軌道結合定数で、これは 基本的に 実験から決めなければならない。
なぜなら この λ は 様々な結合状態や 環境に応じて 変化するからである。
そもそも 非現実的なスピン自体見ることができないのに、スピン・軌道相互作用なるものが 本当に実在するのか 確認することは 不可能である。
例えば、上に述べたように、スピン・軌道相互作用の大きさは ボーア・ゾンマーフェルトの微細構造と 同じくらいの大きさである。
(Fig.30) マグノン、スピン波 = 単なる "数式記号" で 物理ではない。
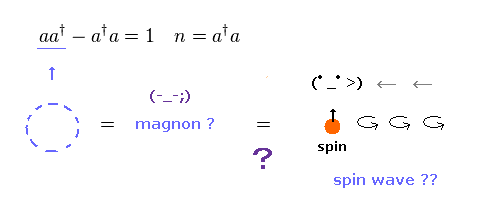
スピン波は 磁性体中を 伝播すると言われている。
それらは "マグノン" と呼ばれ、電子のスピンの 集合的な励起状態であるとされている。
もちろん、このマグノン自体は 非実在的な 準粒子である。
マグノンは "ボソン" であると言われるが 単なる 生成 (= a† ) 消滅 (= a ) 演算子の 数式記号にすぎない。
これらの スピン波は 中性子散乱によって 検出できるとされている。
しかし もちろんのこと 中性子の散乱や エネルギー変化に影響を与える要因は 他にも たくさん存在する。
つまり スピン波自体の存在を 直接証明することは 不可能である。
単なる推測の域をでない。
( そもそも ”準粒子”自体 仮想の粒子で 実在しないわけであるが・・・。)
(Fig.31) 準粒子 "マグノン" が スピン波を生じる ??
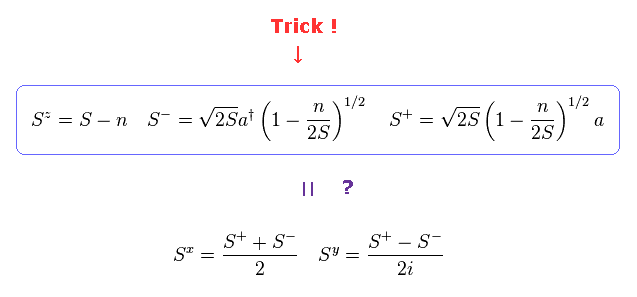
Fig.31 のような 人為的な変換が このホームページで ”スピン”とは 単なる 数式記号で 物理ではない と 何度も繰り返し 説明している 根拠である。
マグノンの 生成 (= a† ) 消滅 (= a ) 演算子 (= Fig.30 ) を用いて、彼らは "スピン" 成分 (= S ) を再現しようとしており、この変換を ホルシュタイン・プリマコフ変換という。
Fig.31 を見て分かるとおり、これらの変換形式自体は 私達人類によって 人為的に導入されたもので、 自然界の真実を 表すものでは まったくない。
(Fig.32) スピンの関係式?
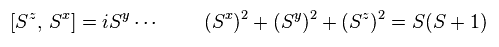
Fig.31 の変換を用いると、Fig.32 のような スピンの関係式が得られる。
そのため 彼らは 準粒子 マグノンが ”スピン波”を生じたと 主張しているのである。
あなたがたは これらの 抽象的すぎる 解釈を 理解できただろうか ?
(Fig.33) スピンのハミルトニアン ?
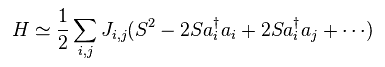
この変換を Fig.26 の ハイゼンベルクのスピン模型に用いて、近似計算を行うと Fig.33 の ハミルトニアンを得る。
Fig.34 のフーリエ変換を Fig.33 にすると、
(Fig.34)
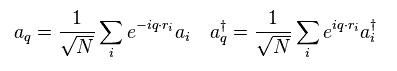
次を得る。
(Fig.35) マグノンの生成 = スピン波のエネルギー ?
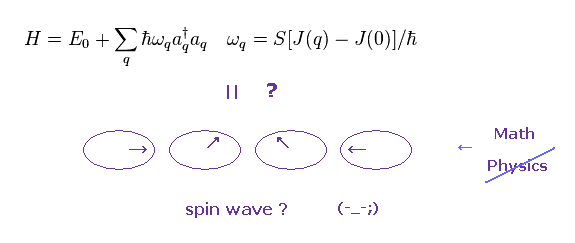
Fig.35 では、 準粒子 マグノン (= a†a ) が 生成されると、スピン波が 生じると 彼らは主張している。
もちろん、私達は これらの非実在的な準粒子や 波を 直接 観察することはできない。
彼らは 散乱された中性子や 光などの エネルギー変化などから これらの存在を 推定しているだけにすぎない。
中性子は 磁気モーメントによっても散乱されるとしているが、他にも これらの散乱結果に影響を与える因子は たくさん存在する。
つまり "スピン波" 自体は 直接確かめられない 単なる 想像上の産物にすぎなのである。
実は スピンを扱う 最新の実験や理論でさえ、非常に人為的な トリックに依存しているのである。
”スピン”のトリック のページには 現在のスピン理論が 単なる数学上の産物であることを示す 良い ( 悪い? ) 例を載せてある。
(Fig.36) ナトリウムの D 線は 単一電子スピンで説明するには 大きすぎ。
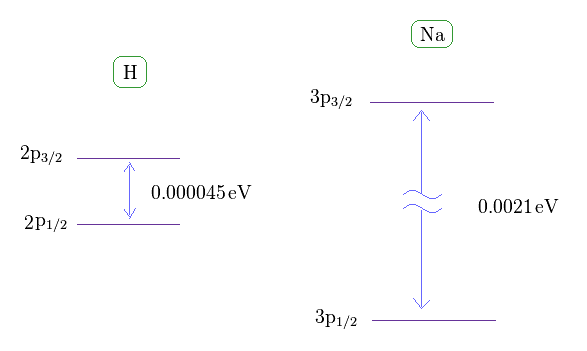
このサイトにあるように、水素の 2p3/2 と 2p1/2 準位間の 微細構造 (= 2重項 ) は 約 0.000045 eV である。
一方で、ナトリウムの 3p3/2 と 3p1/2 準位間の 微細構造は 0.0021 eV もある。 このサイトも参照のこと。
近似的に、ナトリウムの 3p ( もしくは 3s ) 準位の電子は Z = +1 の中心の芯の部分の電荷の周囲を 回っていると見なせる。
( "芯の部分" とは Na の原子核と n=1 と n=2 の軌道に含まれる すべての電子の合計の電荷の意味である。 )
この外殻電子からの視点では、中心の芯電荷は 逆方向に回っており、スピンを持つ電子の部分に 磁場を生じさせることになる。
結果的に スピン・軌道相互作用が生じると彼らは主張している。
(Fig.37) ナトリウムの 芯部分の電荷は Z = 1 よりも はるかに大きい !?

このセクションでは、どうして ナトリウムにおける 大きな微細構造が スピン・軌道相互作用の観点からして 非常に 不合理 であるのか 説明する。
水素とナトリウムの外殻電子 (= 3p ) の両方において、それらが感じる 芯部分の有効電荷は
約 Z = +1e ぐらいになると考えるのが自然である。
しかし これらの H と Na のスピン軌道相互作用間の違いは あまりにも大きい。
これはつまり ナトリウムにおける 有効中心電荷は Z = 1 よりも はるかに大きくなければならない ( Na で Z = 3.54 ぐらいになってしまう )。
この結果は 現実のナトリウム原子の観点からして あまりにも非現実的で 不合理である。
微細構造=スピン軌道は 間違い も参照のこと。
(Fig.38)
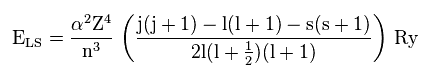
このサイトなどにあるように、スピン。軌道相互作用による エネルギーは Fig.38 のようになる。
α と Ry は 定数であり、主量子数 (= n )、角運動量 (= l )、中心電子 (= Z ) の3つのファクターが この相互作用エネルギーを決定すると言える。
(Fig.39)
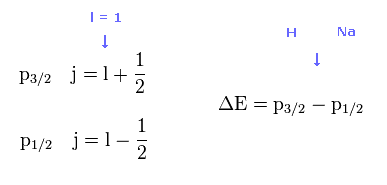
2p (= H ) と 3p (= Na ) の微細構造の両方において、角運動量 (= l ) は 1 に等しい。そのため 全角運動量 j = 1 ± 1/2 は H と Na の両方において 同じになる。
つまり H と Na 間の 違いは 主量子数 ( n = 2, 3 ) と 芯部分の電荷 ( Z = 1 もしくは ? ) のみ に起因することになる。
(Fig.40) p3/2 と p1/2 準位間の エネルギー差。
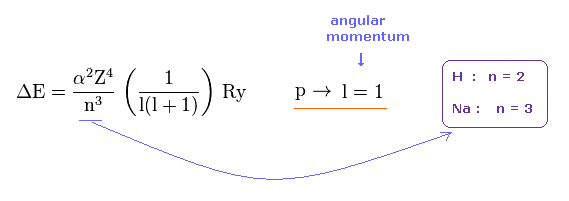
Eq.40 は p3/2 と p1/2 間のエネルギー差を示している。
ここで α は 微細構造定数、 Ry は リュードベリ定数である。
Na と H の主量子数 (= n ) は それぞれ " 3 " と " 2 " である。
つまり 芯部分の電荷 Z が 同じ Z = 1 だとすると、エネルギー差は Na のほうが
小さくなってしまう。
(Fig.41)
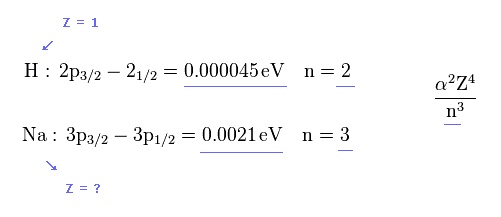
しかし エネルギー差は Na のほうが H よりも はるかに大きい。
( 0.0021 / 0.000045 = 46.6 倍 大きい。 )
つまり Na の 有効芯電荷 (= Z ) は " 1 " よりも はるかに大きくならなければならない。
これは 非常におかしい。
(Fig.42) Na+ の 有効芯電荷が 3.54 にも なってしまう !?
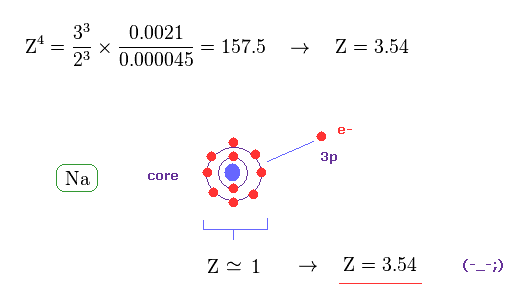
Eq.40 と Eq.41 から、Na の有効芯電荷は Z = 3.54 ほども大きな値になり 現実のナトリウムとは 程遠い値である。
この 芯部分の電荷は すでに述べたように Na の原子核と 1n, 2n 準位に含まれるすべての電子の合計の電荷である。
3s 電子のみを除いた Na+ イオンの電荷は 約 +1e であることから、
Na においても この 芯部分電荷 "Z" は "1" に近づく必要がある。
"Modern Atomic and Nuclear Physics" ( Fujita Yang, Joseph H.Hamilton ) という本の p.144 には次のように書いてある。
-----------------------------------------------------------------------
しかしながら、ナトリウムにおける 3P の分裂の計算は 少し複雑である・・・。
有効電荷 Zeff を Eq.4.42 (= Fig.40 ) に代入して 実験値 ΔU = 2.1 × 10-3 eV を用いて Z を変換すると、 Eq.4.42 ( n = 3, l = 1 ) から Zeff = 3.5 を得る。
----------------------------------------------------------------------
結果的に Na の D 線の微細構造2重項が スピン・軌道相互作用によって生じると考えるのは
あまりにも無理があると言わざるを得ない。
様々なサイトやテキストを見る限り、Na の微細構造が H に比して はるかに大きい 納得のいく説明を見つけることができなかった。
(Fig.43) クーロン、もしくは 大きな (芯部分) 軌道 - 軌道相互作用が Na D 線を分離する
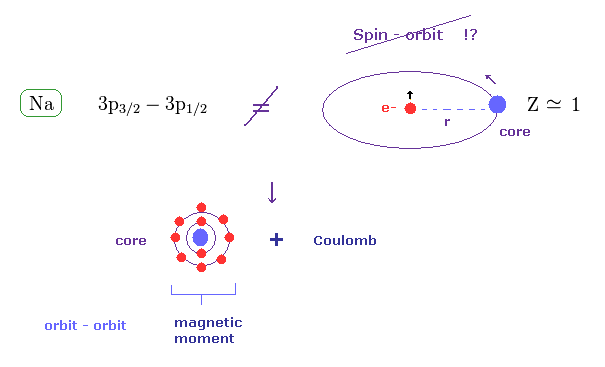
現在の ランデのg因子では Na の 内殻 (= 芯部分 ) の電子に起因する磁気モーメントは まったく考慮されていない。
現実的な視点からして、内殻には 様々な大きな軌道運動が含まれている。
そのため 様々なクーロン相互作用や 内殻電子の 大きな磁気モーメントによって ナトリウムD線の 大きな分離が起きると考えるのが自然である。
スピン・軌道相互作用は ナトリウムの D 線を説明するには 弱すぎである。
(Fig.44)
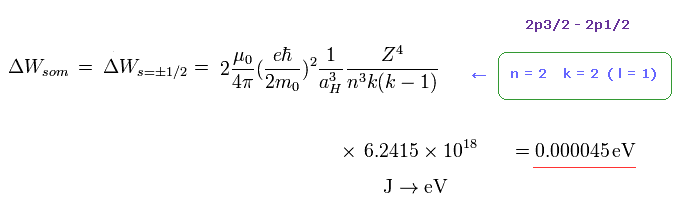
このページや ”スピンはめぐる”( 朝永著 ) の本にあるように、ボーア・ゾンマーフェルト模型の微細構造は トーマス因子を用いたスピン・軌道相互作用の値と ちょうど等しい。
Fig.44 では、" k = 2 " が 軌道の "l = 1" にあたる。
"n = 2" と " k = 2 " を Fig.44 に代入して、2p3/2 と 2p1/2 間のエネルギー準位差は ちょうど 実験値の 0.000045 eV と等しくなる。
つまり ボーア・ゾンマーフェルト模型は 非現実的な "スピン" に頼らずとも この微細構造を 正しく説明することが可能なのである。
Fig.44 によれば、3p と 3d 間の エネルギー差は 約 0.0000044 eV で、これは ラムシフトぐらいになる。
このように 非常に小さなラムシフトは 奇妙な 仮想粒子や 無限大の発散に頼らずとも、他の様々な微小な要因などで説明可能なのである。
(Fig.45) イオン化エネルギーから見た 有効中心電荷 Z は ?
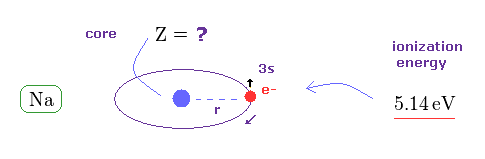
Fig.42 では、もし スピン・軌道相互作用が リアルだとしたら、ナトリウムの 有効中心電荷 Z は "1" よりも はるかに大きく (= 3.54 ) なってしまう。
この芯部分の有効中心電荷は ナトリウムの最外殻 3s 電子の
イオン化エネルギー から知ることができる。
ナトリウムのイオン化エネルギーは 5.14 eV である。
(Fig.46)
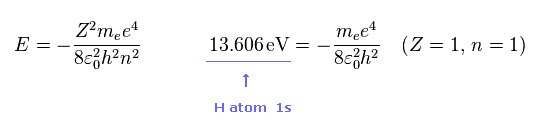
ご存じのとおり、水素の 1s 電子のイオン化エネルギーは 13.606 eV である。
1s の水素では、 Z = 1 と n = 1 である。
(Fig.47)
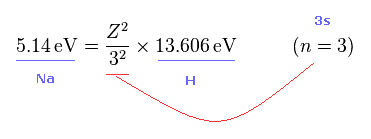
Fig.45 と Fig.46 から、 Fig.47 の関係式を得る。
Fig.47 の Z は 3s 電子の視点からの 有効中心電荷である。
(Fig.48)
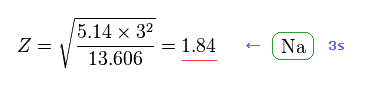
Fig.47 から、 ナトリウムの有効芯電荷として、 Z = 1.84 の値を得る。
この値 (= 1.84 ) は Fig.42 の 3.54 の値とは まったく異なる。
このサイト (p.5, n.48) も参照のこと。
1s と 2s の電子殻には 隙間があるため、3s 電子の感じる有効中心電荷は 通常 "1" よりも少し大きくなる。
しかし もちろん "Z = 3.54" の値は あまりにも 大きすぎであり、リアリティーがない。
(Fig.49)

これは 明らかに 自己矛盾でり、ナトリウムの D 線の スピン・軌道相互作用が 間違いであることを示している。
( もちろん、 3p の電子は Na 原子核から もっと離れているため、この有効芯電荷は 1.84 よりも 小さくならなければならない。 )
このページも参照のこと。
(Fig.50) スピン角運動量は 巨視的に見れるのか?
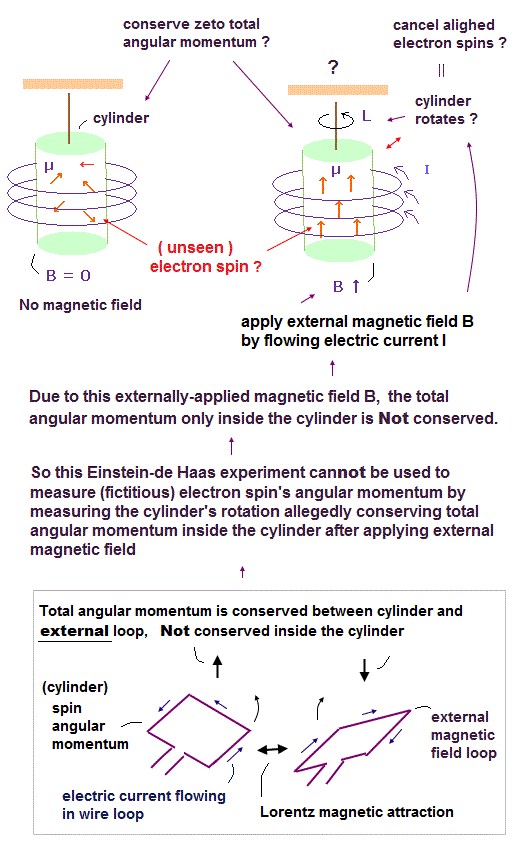
アインシュタイン - ド・ハース効果は "スピン" が "現実に回転していることを示したと言われている。
しかし スピンが 本当に回転だとすると、そのスピン速度は このセクションで 説明した通り、光速よりも はるかに速くなる必要がある。
これは奇妙である。
Fig.50 左図では、円柱内の 磁場 B は ゼロのため、磁気双極子モーメント (= μ ) は ランダムな方向を向いている。
Fig.50 右図では、磁場がかけられ、各 μ が 平行になり 円柱全体が 回転しだす。 このサイト p.4 や
このサイトを参照のこと。
この実験は スピンのg因子が "2" であることを示したと言われている。
しかし この実験は 非常に 難しく、その解釈は かなり 強引と言わざるを得ない。
( 例えば、 各スピンの方向が変わっても、 円柱全体が 回転する必要は まったくない。 )
また アインシュタイン自身の 元の実験は この g因子が 古典的軌道のように 単に
"1" であることを 示しているのである。
(Fig.51) スピン = "本当の" 回転 ?? → スピード > 100 c
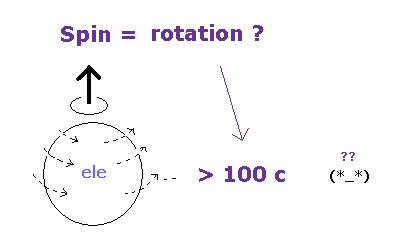
"Einstein's unification" ( Jeroen van Dongen 著 ) の本の 78-79 ページには次のように書いてある。
----------------------------------------
アインシュタインと ド・ハースの 最初の実験では g因子が 1.4 となった。
これは 磁場が弱すぎるためのエラーと思われ、改善した実験では
満足のいく結果が得られた。 この結果は g = 1.02 +- 0.10 だった。 ( ← これは 古典的軌道によるものである。 )
1925 年の 電子スピンの発見は g = "2" となる 理論的考察を与えた。
なら なぜ 上記の実験では g = 1 を与えたのか ?
1つには 地球の磁場の影響が強く、それが 誤差につながったと考えられる。
------------------------------------------
このように オリジナルの実験では 古典的軌道を示す g因子 = "1" を与えていたのである。
また この実験は 地球の磁場の影響に左右されるほど 難しい実験でもある。 このサイトも参照のこと。
(Fig.52) 各スピンは 本当に 円柱全体を回転できるのか?
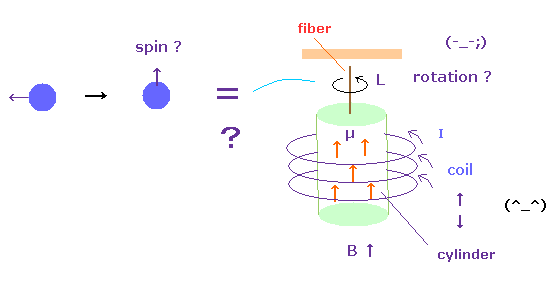
問題は 各スピン角運動量の方向の変化によって 本当に 鉄の円柱全体の回転につながるのかどうか という点である。
もちろん、各電子 ( もしくは 陽子 ) は 互いに 分離している。
これはつまり、 磁場が 各角運動量を変化させるような 力 として働いていることになる。
この磁場は もちろん 真空中も伝達してコイル内の電子に影響を与えられる。
それらの角運動量 (= 磁気モーメント ) は 紐よりも コイルのほうに 伝達されると考えるのが 自然である。
なぜなら そもそも コイル内の電子の運動 (= 電流 I ) に応じて、円柱内のスピンの向きが変わるからである。もしくは ファラディーの電磁誘導の法則を思い出すといい。
つまり コイルと円柱内の電子達が 影響し合う関係にあると考えるのが自然である。
また 各電子スピンが 互いに平行になったからと言って、陽子に影響がなければ、円柱全体が回転することはない。
( 例えば、鉄などの 強磁性体自体 磁気を帯びても回転しているわけではない。)
つまり この実験結果の解釈は あまりにも強引で そのままでは 到底 受け入れ難いものである。

2013/12/29 updated This site is link free.