トップページ (2電子原子も含む正確な新ボーア模型)
奇妙な "スピン" は 実在しない。
1重項、3重項は "スピン" を意味しない。
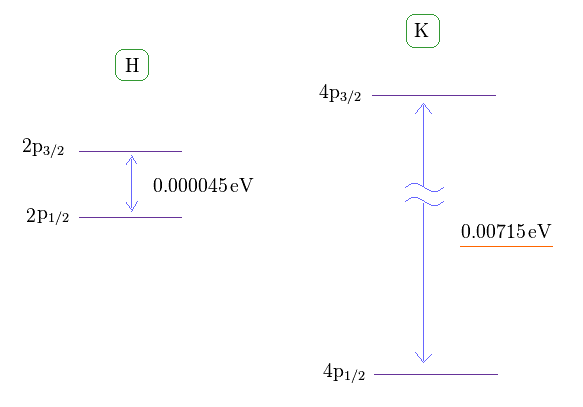
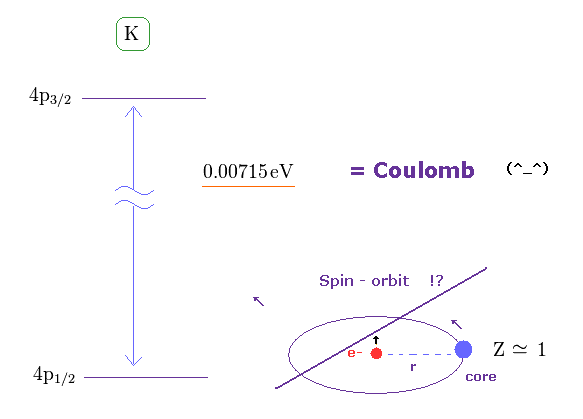
(Fig.1) 水素 (= H ) と カリウム原子 (= K ) の 微細構造 (= D 線 )。

このページでは、ナトリウムの D 線は スピン・軌道相互作用によって生じると考えるには 余りにも大きすぎることを示した。
つまり これら D 線における 非常に大きな効果は 内殻の電子群とのクーロン相互作用によって生じると考えるのが 自然である。
このページでは カリウム (= K )、ルビジウム (= Rb )、セシウム (= Cs ) などの スピン・軌道相互作用は 非現実的なくらい 大きすぎて、 すなわち スピン・軌道という概念自体があり得ないものであることを示す。
このサイトにあるように、 水素原子の 2p3/2 と 2p1/2 間の微細構造 (= 2重項 ) は 約 0.000045 eV (= 0.4 T ) である。
一方、カリウムの 4p3/2 と 4p1/2 間の 微細構造は 0.00715 eV (= 63 T ) ほども大きい。 このサイト や このサイト (p.7, n.67) も参照のこと。
この水素とカリウムの D 線のエネルギー差は 明らかに 違いすぎ ( 0.4 T vs. 63 T ) である。
近似的に、カリウムの 外側の 4p ( もしくは 4s ) 電子は
Z = +1 の 中心の 芯電荷 の周囲を回っていると考えることができる。
( "芯電荷" とは K の原子核と n = 1, 2, 3 の軌道に含まれる すべての電子の合計である。 )
(Fig.2) スピン・軌道相互作用 ? → 中心芯電荷 Z は "大きくなりすぎる"。
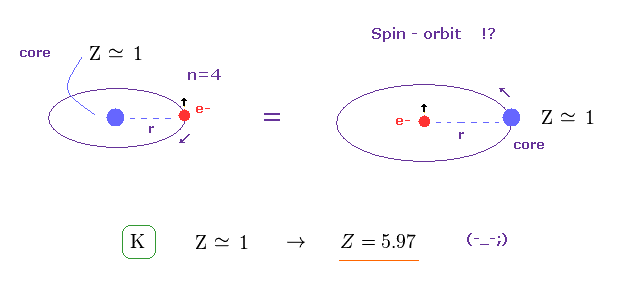
外殻電子の視点からは、 芯 の電荷が 逆方向へ回っていることになり、これが スピンを持つ電子のところに 磁場を引き起こす。
その結果、スピン・軌道相互作用による エネルギーが生じるというのが 彼らの理屈である。
水素 と カリウムの外殻 (= 4p ) 電子の両方において、それらが感じる有効芯電荷の大きさは Z = +1e ぐらいになる必要がある。
しかし H と K のスピン・軌道相互作用の差は 大きすぎである。
計算すると、 カリウムの有効芯電荷は Z = 1 よりも はるかに大きくなってしまうことが分かる ( K で 約 Z = 5.97 )。
この事実は "スピン" という概念が 不合理で 非実在的な存在であることの証しである。
(Fig.3) p3/2 と p1/2 間のエネルギー差。
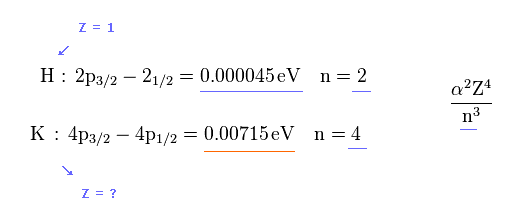
このサイト や
このサイト (p.9) にあるように、スピン・軌道相互作用のエネルギー は Z4 / n3 に比例する。
( Z は 芯電荷、 n は 主量子数、 α は 定数 である。 )
水素原子では、 Z = 1 と n = 2 である。
カリウム原子では、 n =4 である。
これらの値とエネルギー ( 0.000045 eV vs. 0.00715 eV ) から、カリウムの有効芯電荷 Z の値を知ることができる。
(Fig.4) カリウムの Z の値は 大きすぎ (= 5.97 )。
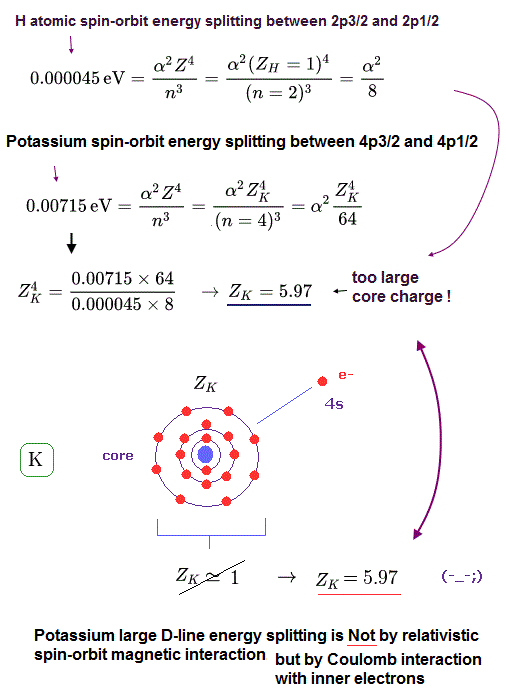
Fig.3 と Fig.4 から、 K の 有効芯電荷の値は Z = 5.97 という 非現実的なくらい 大きな値になってしまう。
何度もいうが、この芯電荷とは K の原子核と 1n, 2n, 3n の 内殻の電子群 すべてを足し合わせた合計の電荷である。
K+ イオン ( 4s 電子のみを除いた ) の電荷は 約 +1e である。
つまり K においても この有効芯電荷 "Z" は "1" に近づく必要がある。
結論からして、カリウムの D 線の分裂が スピン・軌道相互作用によって生じるというという考えは 明らかにあり得ないものである。
様々なウェブサイトや 教科書を見る限り、この大きな差の 適切な理由を見つけることが
できなかった。
(Fig.5) クーロン、大きな (芯の) 軌道 - 軌道 相互作用が "K" の D 線の差の原因。
現在の ランデのg因子の理論では、K の 内殻 (= 芯 ) の 電子群は トータルとして 何の磁気モーメントも持たないことになっている。
しかし 現実的な視点からすれば、内殻の電子達は 非常に大きな 軌道運動をしている。
上記の カリウム D 線の 非常に大きな差は 内殻の電子群との クーロン相互作用や 大きな磁気モーメントによって生じると考えるのが しごく自然と言える。
スピン・軌道相互作用は カリウムの D 線を説明するには どう考えても
弱すぎである。
(Fig.6) イオン化エネルギーからの 有効芯電荷 Z とは?
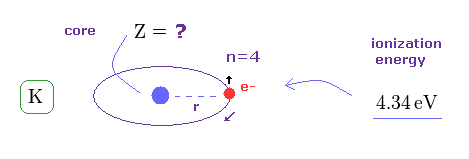
Fig.4 では、もし スピン・軌道相互作用が リアルなものだとしたら、カリウムの有効芯電荷 Z は "1" よりも はるかに大きく (= 5.97 ) なってしまうことを示した。
本当の有効芯電荷は K の 4s 電子の イオン化エネルギーから知ることができる。
カリウムにおける このイオン化エネルギーは 約 4.34 eV である。
(Fig.7) 水素様原子。
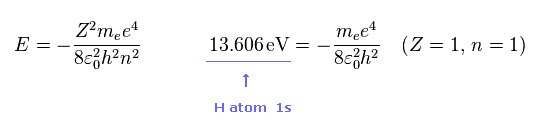
Fig.7 は 水素様原子における 各 "n" と "Z" に対する エネルギー準位である。
ご存じの通り、水素原子の 1s 電子のイオン化エネルギーは 13.606 eV である。
また、水素の 1s では、 Z = 1 と n = 1 である。
(Fig.8) カリウムの 本当の 有効芯電荷は Z = 2.259。

K の 4s 電子の 主量子数 ( n = 4 )、イオン化エネルギー (= 4.34 eV ) と Fig.7 を考慮すれば、有効芯電荷 Z = 2.259 の値を得ることができる。
この 真の 有効芯電荷 (= 2.259 ) の値は Fig.4 の Z = 5.97 の値よりも はるかに小さいものである。
よって カリウムのスピン・軌道結合という概念は 単なる 幻想にすぎない。
(Fig.9) Rb の微細構造。
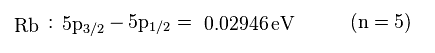
このサイトにあるように、 Rb の 5p3/2 と 5p1/2 準位間の差は 0.02946 eV ほどもある。
この Rb の微細構造も 水素原子 (= 0.000045 eV ) のよりも はるかに大きい。
(Fig.10) 有効芯電荷 Z = 10.25 は 大きすぎる。

カリウムの場合のように、スピン・軌道相互作用と イオン化エネルギーから それぞれの有効芯電荷の大きさを推定できる。
スピン・軌道相互作用による 芯電荷の大きさ ( Z = 10.05 ) は 真の芯電荷 ( Z = 2.77 ) よりも はるかに大きい。
この結果から ルビジウムにおいても スピン・軌道相互作用という概念が間違いであることが分かる。
(Fig.11) Cs の微細構造。
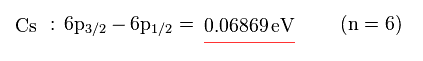
このサイトにあるように、 Cs の 6p3/2 と 6p1/2 準位間の差は 0.06869 eV ほどもある。
この Cs の微細構造も 水素原子 (= 0.000045 eV ) のよりも はるかに大きい。
(Fig.12) 有効芯電荷 Z = 14.248 は 大きすぎる。
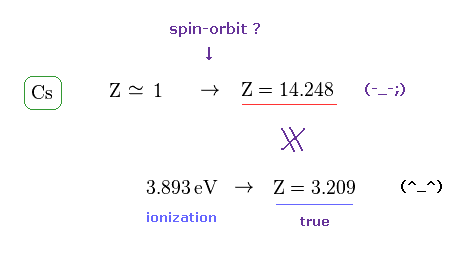
カリウムの場合のように、スピン・軌道相互作用と イオン化エネルギーから それぞれの有効芯電荷の大きさを推定できる。
スピン・軌道相互作用による 芯電荷の大きさ ( Z = 14.248 ) は 真の芯電荷 ( Z = 3.209 ) よりも はるかに大きい。
この結果から セシウムにおいても スピン・軌道相互作用という概念が間違いであることが分かる。
(Fig.13) 金属の 磁化は スピン・軌道 (= LS ) 結合の証明になるのか ?
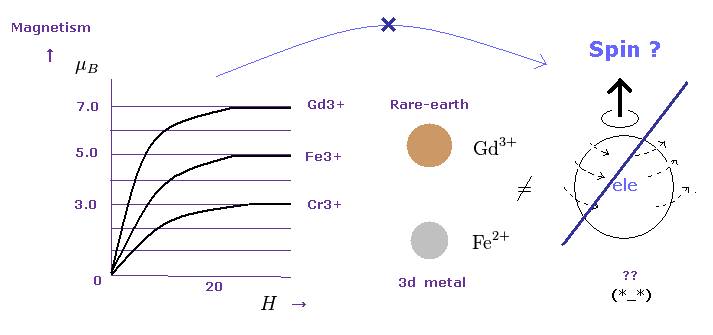
奇妙な スピンの 主要な実験的根拠は 4f 族の レア・アース (= 希土類 ) 元素の磁化測定結果にあると言っていい。
量子力学によれば、ある磁場のもとでの 磁化の性質は ランデのg因子 ( このサイト 参照のこと ) と LS 結合の規則に従う必要がある。
実は、Ti, V、 Cr、 Mn、 Co、 Ni、Cu などの
"3d" 系の 遷移金属は ランデの g因子に まったく 従わないことが知られている。
つまり 実験的証拠というのは 4f 系の 希土類金属のイオンのみなのである。
他のすべての元素は 単純なランデのg因子で表せないほど 複雑な磁化性を示す。
( 試しに "有効ボーア磁子数" などで検索してもらうと分かるが、希土類金属系しか インターネット上で 出てこない。)
希土類金属イオンにおいても 実験値に合わせるために 非常に人為的なルールを採用している。
つまり 様々な金属における スピン・軌道相互作用は 非常に 疑わしく かつ 非現実的であることが分かる。
(Fig.14) "3d" 軌道の 軌道角運動量 (= L ) を すべてゼロにする ? ← トリック。

標準的な量子力学によれば、"3d" 軌道の 角運動量は L = 2 で、ゼロでは ない。
しかし "3d" の金属イオンでは、スピン・軌道相互作用 (+ フントの規則 ) による計算結果は このままでは 実験値と まったく異なるものになってしまう。
それらを 実験データに 合わせるために、彼らは 突如 3d 軌道の角運動量をすべて 削除してしまった。
( このサイト (p.426) や このサイト p.59 も参照のこと。 )
これは 明らかに 人為的なルールで スピン軌道相互作用 ( フントの規則と ランデのg因子 ) のルールが 破れていることの証拠である。
現在の解釈によれば、 遷移金属イオンは 隣接する 他のイオンからの影響で その軌道角運動量成分のみ キャンセルされて すべてゼロになってしまう ( → L = 0 ) らしい。
しかし この解釈は あまりにも 都合よく かつ 強引なものである。
同じ磁気モーメントなのに スピンのほうは まったくの無傷で、 軌道のほうだけ ゼロ になってしまう ?
どうやって 自然界は 都合よく これらを区別しているのだろうか?
(Fig.15) "4f" 軌道は "4d" 軌道から 離れすぎ。 ← これもまた 人為的なトリック。
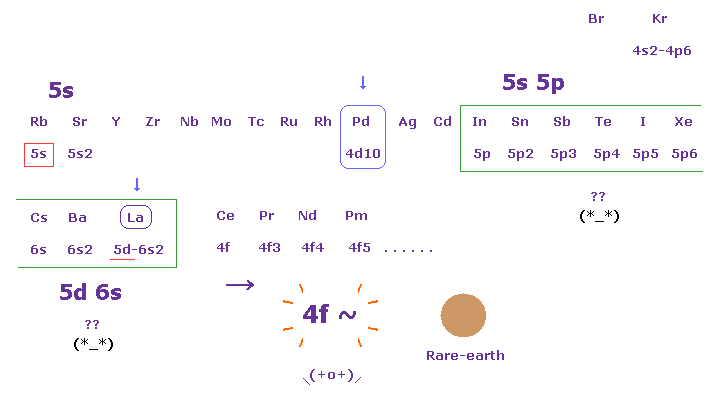
"3d" 金属と違い、 "4f" の希土類元素のイオンは 実験値に 近い値を出すことが知られている。
( このサイト (p.425) もしくは このサイト p.59 を参照のこと。 )
しかし 実際は、彼らは あるトリックを この希土類金属に対して使っているのである。
そのトリックの1つが 周期表における 4f 軌道の位置である。
Fig.15 に示したように、 5s, 5p, 5d, 6s などの 本来 上位のエネルギー準位であるものが 4f 軌道よりも前 に 次々と登場している。
パラジウム (= Pd ) において、すでに 4d 軌道のすべてが 埋まった状態になっているのだが、 "Ce" まで "4f" 軌道が現れるのを ずっと 待たなければならないのである。
(Fig.16) イオン化 : Nd → Nd3+. 5s と 5p の電子が スキップされる ?
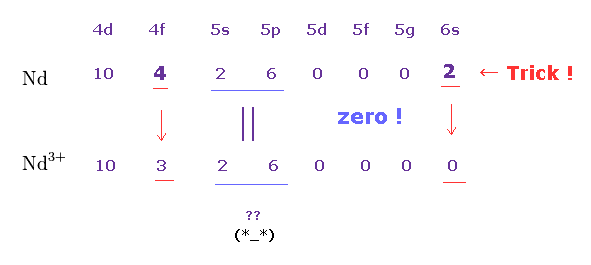
驚くことに、希土類金属のイオン化は Fig.16 に示したような 非常に 不合理な ルールに従う必要があるのである。
Nd から Nd3+ へのイオン化で、 6s と 4f に属する 3つの電子が 取り除かれる。
一方で、 5s と 5p の電子は まったくの 無傷である。
Fig.15 で 6s 軌道が 4f 軌道よりも先にきているということは、6s 軌道のほうが 4f 軌道よりも エネルギーが 低い ということだろうか?
( n が 2つも 上の準位よりも 4f 軌道のエネルギーは 高いということになってしまう。)
この "6s" 軌道へのあり得ないジャンプは Cs の D 線の説明に必要なものである。
彼らは 5s と 5p の軌道は 4f の 外側にあって、内部を遮蔽していると言っている。
ならば、Nd3+ イオンにおいて 4f の代わりに 5p の電子が 先に取り除かれるのが筋であろう。
これらの解釈は 明らかに 自己矛盾しており 実験値に合わせるための トリックと言える。
(Fig.17) J = L -S もしくは J = L + S ?? ← トリック。
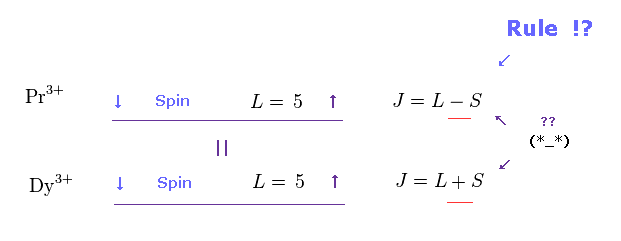
後で説明するが、4f の前半と後半の希土類において 彼らは 異なったルールを採用している。
Fig.17 の上のケースでは、 J = L - S の関係式を用いている。
Fig.17 の下のケースでは、 J = L + S の関係式を用いている。
角運動量とスピンの方向は 両者で 変化していないのに、その符号を 意図的に変えてしまった。
他の様々な原子やイオンをチェックした限り、この アドホックなルールは 希土類金属のためだけに導入されたといっていい。
( なぜなら 純粋な有効ボーア磁子数は 4f の希土類イオンのみに通用する概念だからである。 )
このサイト (table 4) は "4f" 軌道のみを除いた 3d, 4d, 5d, 5f などの他の全ての軌道は 周囲の配位場の影響が強すぎて 単純なランデのg因子や フントの規則を 満たさないと言っている。
(Eq.1)
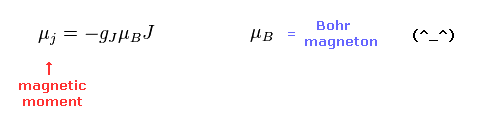
Eq.1 は ある原子 (イオン) における 磁気モーメントである。
μB は ボーア磁子で、その大きさは ボーアの基底状態の磁気モーメントに ちょうど等しい。
"J" は L と S を結合した 全角運動量である。
(Eq.2) gJ = ランデの g因子。
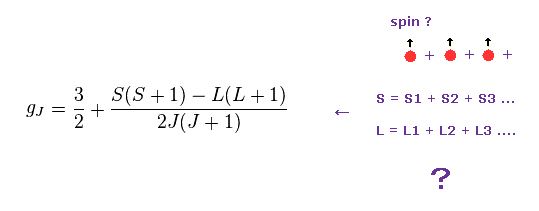
このページに示したように、ランデのg因子 (= gJ ) は 非常に 不自然な歳差運動の仮定に頼っている。
多電子原子では、Eq.2 のように 各スピンを足していく必要があると 彼らは主張している。
磁気モーメントという概念自体は スピンと軌道由来のものか 区別できないはずなのに、LS 結合ルールでは それらを明確に区別する必要がある。
( 例えば、 S = S1 + S2 + S3 .. , L = L1 + L2 + L3 .. のように。)
(Eq.3) E = 磁気エネルギー。
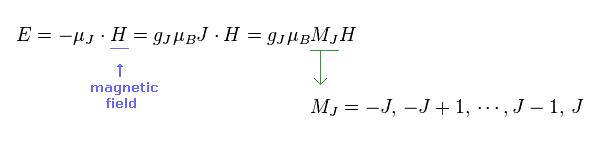
ある外磁場 H の下で、磁気エネルギー E は 磁気モーメント (= μJ ) × H で与えられる。
MJ は H 方向への J の成分である。
(Eq.4)
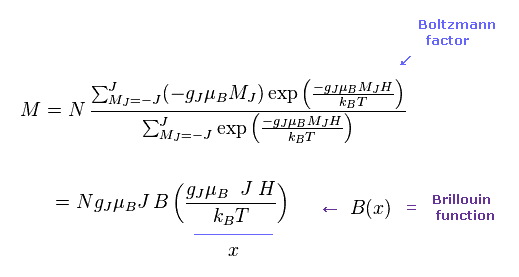
あるエネルギー状態の確率密度は ボルツマン因子で与えられる。
そのため 平均の磁気モーメント M は Eq.4 のようになる。
B(x) は "ブリユアン関数" と呼ばれるものである。
(Eq.5)
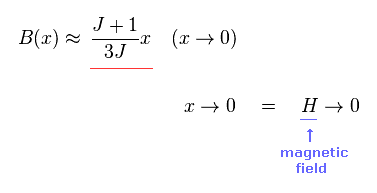
有効ボーア磁子数を得るには 磁場 H が ゼロ の極限 ( H → 0 ) の状態を考える必要がある。
Eq.5 を用いると、 Eq.4 は、
(Eq.6) H → 0 の極限での 有効ボーア磁子数。
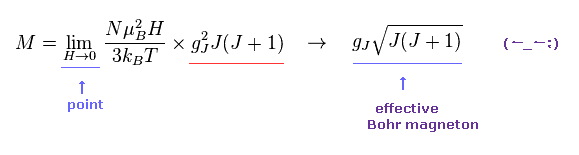
H → 0 の極限で、 J(J+1) の 平方根を含む 有効ボーア磁子数を得ることができる。
( ここでは この J(J+1) という概念は ボルツマン因子という 純粋な古典力学的手法によって 得られたものであることを 心に留めておく必要がある。 )
重要な点は H → 0 の極限で 磁化を測定することは 非常に難しいということである。
なぜなら 非常に弱い H の下では、様々な 他の効果、温度ゆらぎなどの影響を 無視 できないからである。
つまり この有効ボーア磁子数は H > 0 のデータを基に外挿法によって得る必要がある。
(Eq.7)
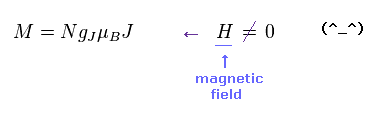
外磁場 H が 十分に強いとき、金属の 磁気モーメント (= M ) は Eq.7 のようになる。
Eq.7 は J(J+1) の 平方根を 含んでいない。
十分な H の下での Eq.7 の値は 非常に弱い H での Eq.6 より はるかに 信頼できる結果であることは言うまでもない。
このサイト ( p.4-6 ) も参照のこと。
(Fig.18) H → 0 の極限での 有効ボーア磁子数は 信頼できる?
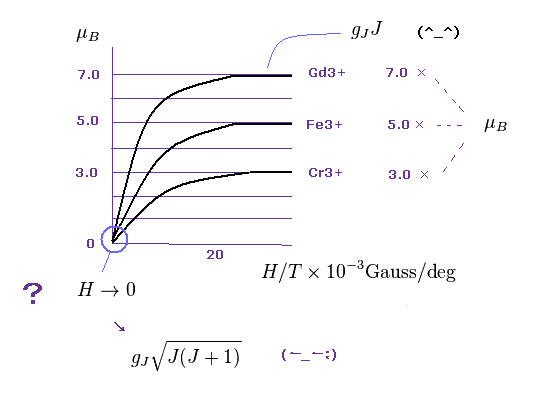
このサイト (p.422) にあるように、 様々な金属 ( イオン ) の磁化は ある十分な H の下で、 ボーア磁子 (= μB ) の整数倍になる。
この結果は これらの金属において 何らかの ボーア軌道の量子化のルールが働いていることを示している。
一方で、J(J+1) を含む 有効ボーア磁子数は H → 0 の極限での 磁化曲線の傾きから 得られる。
つまり この結果は 容易に 他の影響を受けるため、慎重に判断する必要がある。
(Fig.19) ランデのg因子を満たさない。 → 角運動量をゼロにしてしまう L = 0 !?

すでに述べたように、 "3d" の遷移金属イオンは ランデのg因子 と LS 結合の規則を 満たさない。
そこで 実験値に合わせるために 突然 すべての角運動量をゼロ ( L = 0 ) にしてしまった。
これは 非常に理不尽である。
なぜなら スピンによって生じる磁気モーメントのみを 意図的に 残してしまったからである。
自然界の法則は どのように スピンか軌道運動かによる 磁気モーメントの
区別を しているのだろうか?
かなり 出来すぎた 解釈である。
(Fig.20) バナジウムイオン ( V3+ ) : L = 3 → L = 0 !?
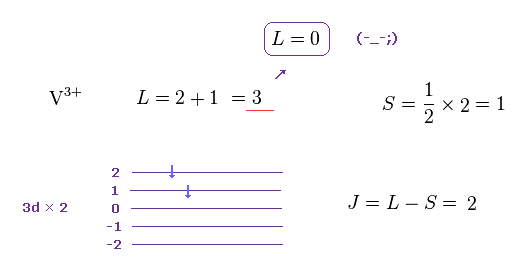
例えば、バナジウムイオン ( V3+ ) は 3d 軌道に 2つの外殻電子を持つ。
フントの規則 ( このサイト参照 ) によれば、 V3+ の軌道角運動量 (= L ) は 2+1 = 3 になる。
また 全スピン角運動量は S = 1 である。
"3d" 軌道は 明らかに 軌道運動を含んでいるのに、彼らは 突然 それらを削除してしまった ( L = 3 → L = 0 )。
このトリックは 明らかに おかしい。
周囲の環境は どのように これらスピンと軌道運動の磁気モーメントを 便利に
区別しているのだろうか?
いずれにしろ 3d 金属のイオンが ランデのg因子などの法則を まったく満たさないことは理解されたと思われる。
(Fig.21) V3+ イオンの磁気モーメントは ちょうど 2.0 × ボーア磁子 (= μB ) !?
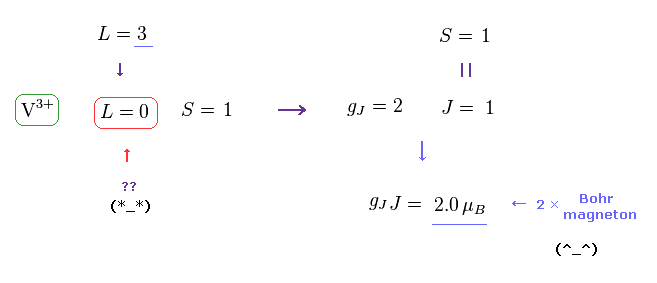
もし 角運動量 (= L ) が ゼロなら、スピンしか残らず、 ランデのg因子は 非常に 単純 ( gJ = 2 ) になる。
また 全角運動量 J は S に等しくなる ( J = S )。
V3+ では、飽和磁化 (= gJJ, Fig.18 の平坦線 ) の値は ちょうど 2.0 × ボーア磁子になり、また 他のすべての 3d 金属においても ボーア・ゾンマーフェルトの量子化の規則が 成り立っていることが分かる。
(Fig.22) すべての 3d 金属イオンで ボーアの量子化条件が有効である。

S(S+1) の平方根は 所謂 架空の歳差運動状態であり、直接 確認することが できない。
確認できる実験値 (= gJJ ) は Fig.22 に示したように、すべて ボーア磁子 (= μB ) の 整数倍 になる。
よって ボーアの量子化条件が これらのイオンで成り立っていることが分かる。
(Fig.18) 十分な H の下での 飽和磁化 (= gJJ ) 。

中性の "3d" 金属は 周囲の原子の影響で 非常に複雑な磁化を示すため もちろん、単純な ランデのg因子や LS 結合の法則を満たさない。
つまり 中性の遷移金属では これら局在理論が成り立たず、まったく別の理論を必要とすることが知られている。
(Fig.23) 希土類金属イオンは LS 結合を満たす ?
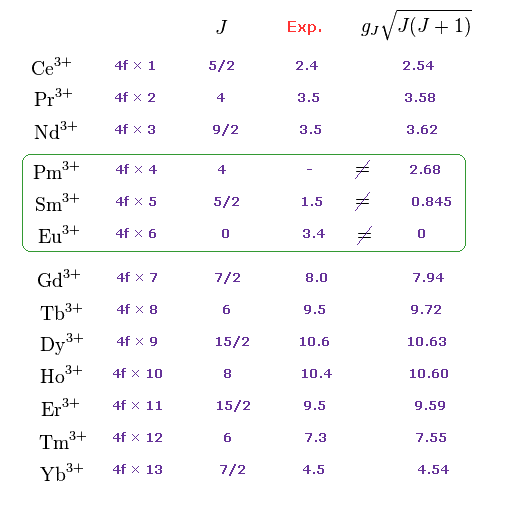
3d 遷移金属イオンと異なり。 "4f" 希土類金属イオンは LS 結合のルールにほぼ従うことが知られている。
"gJ" は ランデのg因子で Eq.2 から得られる。
しかし すでに述べたように、それらを実験値に一致させるには 様々な
アドホックなルールに頼る必要がある ( Fig.15、 16、 17 ) を参照のこと。
これらのルールを人為的に こしらえたとしても Fig.23 に示したように まだ 3つの希土類金属イオンが ランデのg因子に従わない。
つまり これら3つの元素は トリックの 限界を表していると言える。
(Fig.24) "gJJ" は ボーア磁子の 整数倍になる。
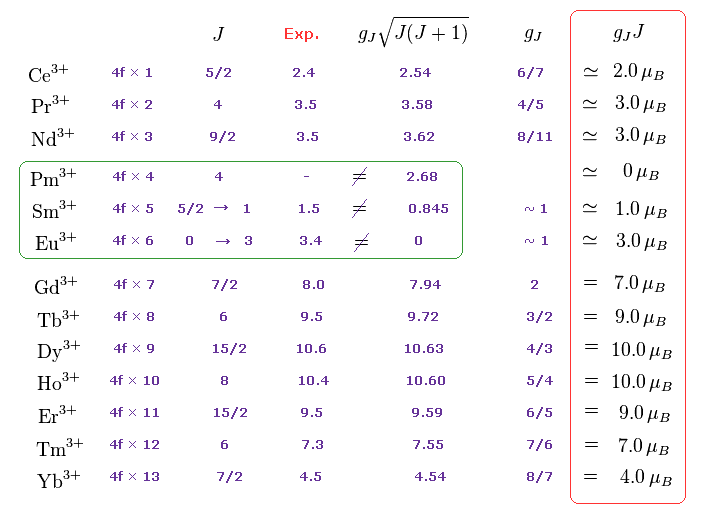
通常の教科書のほとんどすべてが 実験結果を J(J+1) の平方根を含む 有効ボーア磁子数として紹介している。
しかし これらの平方根は 架空の歳差運動状態であり、実験で 直接確かめられないものである。.
飽和磁化 (= Fig.18 の 平坦線 gJJ ) が 真の 磁化性を表している。
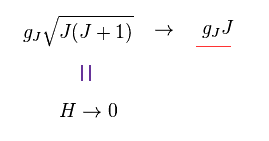
驚くことに、Fig.24 に示したように ほぼすべての希土類金属イオンも gJJ に関して ボーアの量子化条件に従う。
これらの結果は ドブロイ波の 量子化条件が すべての原子やイオンにおいて 重要な役割を果たしていることを表している。
(Fig.25) "4f" の希土類金属の位置は 4d 元素のはるかかなた。

お気づきのとおり、"4f" の希土類金属の位置は 実験値に合わせるためにわざと 不自然な位置に配置させたといっていい。
Pd の原子においてすでに 4d のすべての軌道が 埋まっている。 (= 4d × 10 ).
"4f" 軌道の前に 5s, 5p, 6s, 5d などの もっと高いエネルギー準位が 次々に挟み込まれている。
(Fig.26) イオン化 : Nd → Nd3+. 5s と 5p の電子がスキップされた?

奇妙なことに、現在の量子力学では "6s" 軌道が "4f" 軌道よりも 低い のである。
( "4d" < 5s < 5p < 6s < 5d < "4f". ← トリック。 )
周期表における この "6s" の不自然な位置は Cs の D 線を説明するために必須なものである。
n = 4, 5 軌道 (= 4f, 5d, 5f, 5g ) を スキップして 6s まで ジャンプしてしまうことは 非常に理不尽で 受け入れ難い。
(Fig.27) J = L - S か J = L + S の どっちが本当 ?
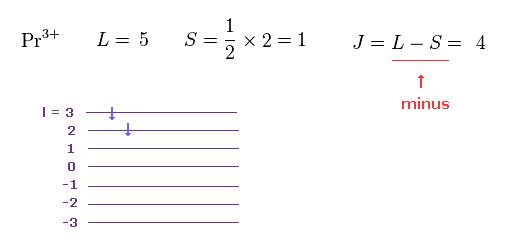
Pr3+ ( プラセオジムイオン ) は 4f 軌道に 2つの電子を持つ。
基本的な フントの規則によれば、軌道 (= L ) と スピン (= S ) 角運動量は Fig.27 に示したように、 "5" と "1" に それぞれなる。
重要な点は "4f" の希土類金属の 約半分は J = L + S の代わりに J = L - S を満たす必要がある。
様々なサイトなどをチェックした限り、この アドホックなルールは これら 希土類金属イオンのみの実験結果を説明するために導入されたと言っていい。 このサイトなども参照のこと。
(Fig.28) ジスプロシウムイオン ( DY3+ ) は J = L + S !?
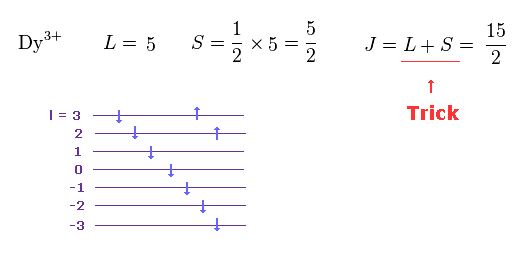
一方で、Dy3+ では、J = L + S という まったく異なる式を利用している。
この使い分けは 非常におかしい。
Fig.27 と Fig.28 に示したように、 各軌道とスピンの方向は 自然には 変わらないはずである。
彼らは どちらか一方の共通の式 J = L + S ( もしくは L - S ) を使用すべきである。
(Fig.29) 方向は変わらない。 → J = L ± S は 人為的なトリック。
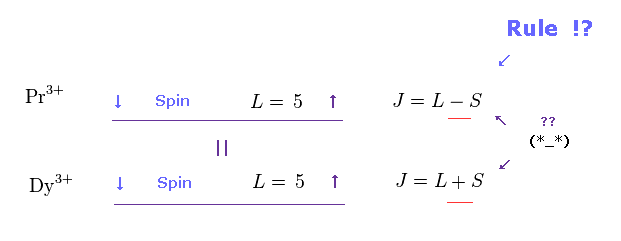
Fig.29' に示したように、1つの電子が入って Gd3+ から Tb3+ に移行した瞬間に すべてのスピンの方向が 逆転してしまうことになる。
これら 賢い "スピン"達は どのように フントの規則を適切に判断して従っているのだろうか?
あまりにも 出来すぎた規則と言える。
(Fig.29') Gd3+ から Tb3+ に移行するとき、すべてのスピン方向が 逆転?
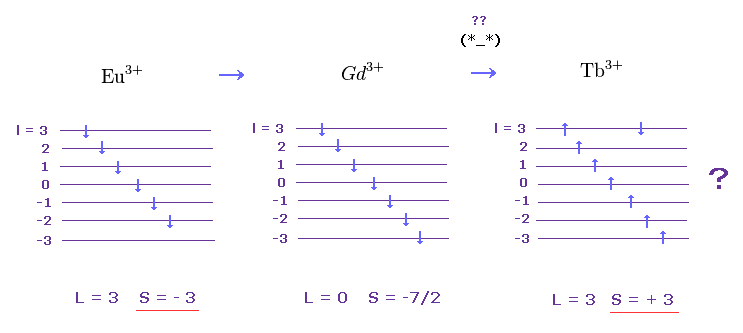
このルールは 4f 希土類イオンのみに有効であり、すなわち 4f 金属のためだけに 導入されたと言っていい。
例えば すでに Fig.19 で述べたように、 "3d" 遷移金属イオンでは LS カップリング規則が 破れている。
このサイト (table 4) にあるように、4f のみを除いた 3d, 4d, 5d, 5f の他のすべての軌道では 周囲からの結晶場の影響が 強くなりすぎて無視できないことになっている。
これはつまり ほぼすべての軌道は 単純なランデのg因子 と フントの規則に 従っていないのである。
Physics 1971-1980 ( Stig Lundqvist 著 ) の教科書の 358 ページには次のように書かれてある。
-----------------------------------------------------
1925 年、フントは 希土類元素の化合物が 経験則を非常に満足しているという論文を書いた。
彼は ランデのg因子と フントの規則を活用した・・・。
--------------------------------------------------
そして 1932 年に、 Van Vleck が この理論を Eu と Sm まで拡張させた。
(Fig.30) 飽和磁化 = gJ J.
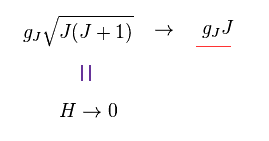
すでに述べたように、J(J+1) の平方根を含む 有効ボーア磁子数は 架空の歳差運動状態であり 実験で直接確認できない。
( 外磁場 H が ゼロに近い極限でのみ この関係式が 模擬的に現れるだけである。 )
(Fig.31) H → 0 の極限の 有効ボーア磁子数は 信用できる?

もちろん、磁場 H が非常に弱いとき ( H → 0 )、様々なノイズや 他の効果が無視できず、 エラーが起きやすくなることは言うまでもない。
飽和磁化 (= gJJ = Fig.31 の曲線の平坦部分 ) を見れば、希土類の磁化も ボーア磁子 (= μB ) の整数倍に近くなることが 分かる。
(Fig.32) セリウムイオン ( Ce3+ )。。
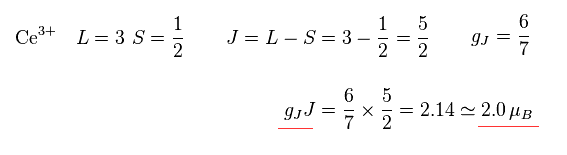
(Fig.33) Pr3+ と Nd3+ イオン。
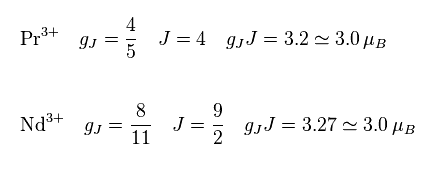
Fig.32 と Fig.33 に示したように、Ce3+, Pr3+, Nd3+ の飽和磁化 (= gJJ ) は すべて ボーア磁子の整数倍に 近くなることが分かる。
(Fig.34) これらのイオンは ちょうど ボーア磁子の整数倍。
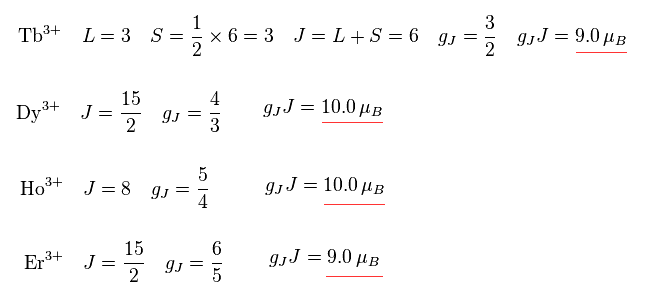
Tb3+、 Dy3+、 Ho3+、 Er3+ などのケースは より際立っている。
それらは ちょうど ボーア磁子の整数倍である。
つまり 多電子の希土類金属においても ボーアの量子化条件が
ほぼ有効であることが分かる。
(Fig.35)
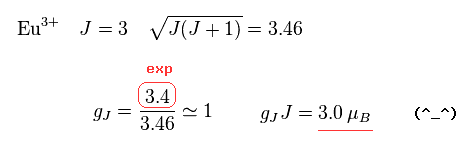
Fig.23 に示したように、 ランデのg因子と LS 結合の規則は Eu3+ と Sm3+ で 完全に破れている。
( 彼らは この不一致を修正するために 別の効果を付け足そうとしているが、この時点で 自然な結果とは言えなくなる。 )
Eu3+ の全軌道角運動量が ちょうど "3" と仮定すると、 gJ は ほぼ "1" になる。
結果的に gJJ は ちょうど 3.0 μB になる。
(Fig.36)
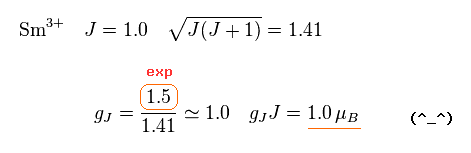
同様に Sm3+ の外殻電子の全角運動量を"1.0" と仮定すると、 gJ は また "1.0" になる。
結果、 gJJ は ちょうど 1.0 μB になる。
(Fig.37) "gJJ" は 希土類イオンでも ほぼボーア磁子の整数倍になる。

Pm3+ イオンでも 通常の LS 結合規則が通用していない。
彼らは Pm3+ の磁化のデータをとるのが 非常に難しくて できないと主張している。
しかし Fig.37 を見て分かるように、Pm3+ の 磁化は おそらく ほぼゼロになると考えるのが自然である。
これが Pm3+ の磁化の測定が難しかった理由と思われる。
"4f" 元素の 周期表における 不自然な 位置、J = L - S などの 人為的な 規則を採用してもなお Pm3+, Sm3+, Eu3+ の3つの希土類イオンが LS 結合規則を満足しない。
この結果は これらの人為的なトリックの トリックゆえの 限界を露呈していると言える。

2014/1/25 updated This site is link free.