
トップページ (2電子原子も含む正確な新ボーア模型)
スピンが 幻想であることの確認。
BCS 理論における 計算間違い。
(Fig.1) "スピン" 自体に リアリティーなし。 → 様々な人為的なトリックが生まれる。

このページに示したように、超光速のスピン速度やら何かで スピン自体には 何の リアリティーも 存在しない ことが分かる。
つまり 非現実的な "スピン" を説明するには 非常に抽象的な 数学上の演算子を使用するしかない。
もちろん、スピン自体が 非現実的な概念だとすると、パウリの排他原理や スピン・軌道相互作用を "スピン" を用いて 正確に表すことは できない。
これらの抽象的な数学的記号は 実験結果に合わせるように 容易 かつ 意図的に操作できる。
このページでは、”スピン”についての 様々な 人為的なトリックを紹介し、これらの手段に頼らなければならない現状は "スピン" 自体が 実在しないことの証拠であることを示す。
(Fig.2) 磁化率 χ と 温度 T。

キュリー・ワイスの法則は 強磁性の キュリー温度 (= Tc ) 以上における常磁性相における 磁化率 χ を説明することができる。 様々な物質で 近似的に この法則が成り立つことが知られているが、 もちろん 現実の物質では もっと複雑な性質を示すものも多い。
重要な点は この法則は 古典力学に基づいているという点である。
なぜなら この規則が生まれた 1907 年は 量子力学が生まれる前の年だからである。
(Eq.1) 古典的な磁気モーメント ?

最初に P. Langevin は 1905 年に 金属の 各原子は 何かしらの ( 古典的な ) 磁気モーメント (= M ) を持つと考えた。
外磁場 (= H ) のもとで、磁気エネルギーは "-MH" となる。
また 磁化率 (= χ ) は 磁気モーメントを 磁場で割ると 得られる ( χ = M / H )。
(Eq.2) Langevin による キュリーの法則。

ボルツマン分布則 (= e-E/kT ) を用いて、彼は 近似的に キュリーの法則を得ることができた。
キュリー定数 C を 実験で測定すると、様々な金属における 近似的な磁気モーメント "M" を知ることができる。
(Eq.3) キュリー・ワイス則

1907 年に、ワイスは 他の原子から磁気の影響も考慮して計算し直した。
"ΓM" は 他の原子からの 内因性の磁場である。
結果的に 磁化率と温度の関係は Eq.3 のようになる。
このキュリー・ワイス則は 様々な金属で成り立つことが知られている。
また この法則は 強磁性体と常磁性体間の 相転移を説明できたという点で 重要である。
ストーナー ( Stoner-Wohlfarth, SW ) 理論は 磁化率と温度間の関係などを予測することができる。
しかし 一方で ストーナー理論による予測値は とりわけ 常磁性相における 実験値と
食い違うことが知られている。
(Eq.4) 磁気モーメント M ? スピンモデル ?

現在の物性物理学では、各粒子を表すのに 非常に抽象的な演算子に頼るしか方法がない。
Eq.4 では、電子の "up" と "down" スピンの差が 磁気モーメント (= M ) を生じるとしている。
( もちろん、これらのスピンは 単なる数式記号の域を 越えられない。 )
全原子数 (= N ) は up と down スピンの合計である。
(Fig.3) 磁気モーメントの起源は? → "スピン" 意外に選択肢なし?

現在の量子論では、最初から 磁気モーメントを起こす 前提条件として 非実在的な スピン 以外に 眼中になく、他の選択肢を選ぶことができないという 非常に奇妙な状態になっている。
そのため、物性物理分野の論文では 必ずと言っていいほど "スピン" というワードを見かけることになる。他に選択肢がないのだから 当たり前の話である。
その割に、 スピンとは 一体全体何なのかと 彼らに質問したとしても 誰一人として 具体的なものを示すことができない。
ひも理論 などは この非現実的な演算子の なれの果てである。何のリアリティーもないことは一目瞭然である。
( 信じる人だけが こういう分野に進むという 困ったフィルタリング効果が働いていて 現在の物理学全体を歪めている。困ったものである。)
(Eq.5) up と down の スピンの数。

Eq.4 から、Eq.5 のように up と down の 各スピンの数 (= n ) を得ることができる。
(Eq.6) スピン模型 ?

ハバードモデルは 有効ハミルトニアンとして 頻繁に使用され、それには 2種類の相互作用が含まれている。
2項目は 電子間の磁気相互作用で、3項目の M と H は それぞれ 全磁気モーメントと 外磁場である。
( つまり この3番目の項が 全磁気エネルギーである。 )
しかし Eq.6 を見て分かるとおり、物性物理における この模型は 様々な複雑な現象を説明するには
余りにも抽象的すぎる。
さらに、相互作用を表す "U" などのパラメーターを 実験値に合うように 人為的に調節しているだけにすぎない。
(Eq.7) 数演算子。

通常の場の量子論のように、数演算子 (= n ) は 伝導電子の 生成 (= c† ) 消滅 (= c ) 演算子 によって構成されている。
何度も繰り返すように、この数式記号は 見たまま 数式記号にすぎない。
(Eq.8) 反交換関係。

フェルミ粒子は Eq.8 のような 反交換関係を満たす必要がある。
もちろん、実際の電子が こういう演算子の姿かたちをしているわけでもない。
(Eq.9) 反交換 = パウリの排他原理 ?
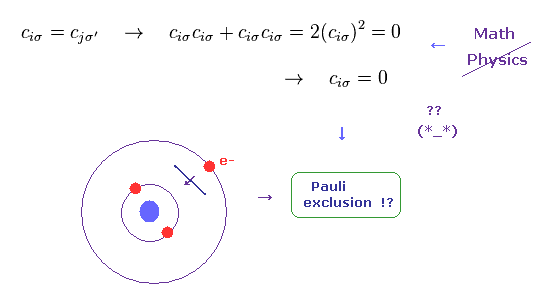
現在の場の量子論によれば、パウリの排他原理の起源 (= 力 ) は 演算子間の
反交換関係であるとしている。
もし あなたがたが 物理学者の誰かしらに このパウリの排他原理の反発力について質問しても、この抽象的な 演算子の関係以上の 具体的なものは 何も示すことが できないだろう。
お気づきのとおり、明らかに これ以上何も問おうとしない 現在の物理の姿勢が 自身の発展を妨げていることは明白である。
もし これらの演算子が 反交換を満たすと、c = c のとき、それらは ゼロになる。なぜなら
cc + cc = 0 だからである。
これが パウリの排他原理のメカニズムということになっている。
これだけの模型だけで はたして 納得できる人は いるだろうか?
(Eq.10) 人為的なトリック。

ここで Eq.6 の2項目を Eq.10 のように変更した。
これは 明らかに 実験結果を得るための 人為的なトリックである。
ある項を 3つに分離した後に、理論にとって便利な項のみ ピックアップしている。
BCS 理論のトリック。
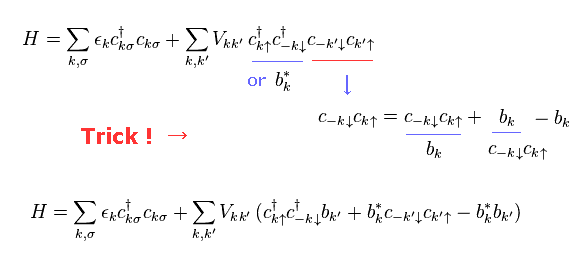
Eq,10 のトリックは BCS 理論のものに似ている。
( BCS 理論 の Eq.19' を参照のこと。 )
BCS においても、2つの余分な項 (= b - b ) を付け足した後に、便利な項のみ ピックアップしている。
この数学的な技巧のみに走っているのが 現在の "スピン" 理論の 実態 なのである。
これでも まだ あなたがたは "スピン" を信じることができるだろうか?
(Eq.11)
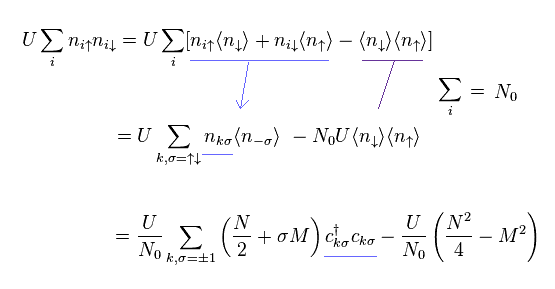
Eq.5、 Eq.7、 Eq.10 を用いて Eq.11 を得る。
(Eq.12)

Eq.11 では、各項において "n" と "c†c" のどちらがいいか 選んでいるだけである。
これも 意図的な操作の1つである。
(Eq.13)
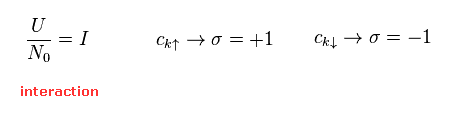
Eq.11 で、Eq.13 の表記が使われている。
"c" が "up" スピンのとき、 σ は "1" になる。
"c" が "down" スピンのとき、 σ は "-1" になる。
(Eq.14)

Eq.4 を用いて、磁気モーメントと エネルギーは Eq.14 のようになる。
ここでは "h" は 2μBH ( "H" は 外磁場 ) である。
(Eq.15)
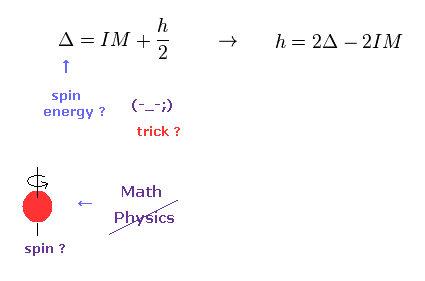
Eq.11 と Eq.14 の σ の項から スピンのエネルギー Δ が 得られるとしている。
しかし Eq.11 を見て分かる通り、 彼らは Δ に都合のいい項をピックアップしているだけである。
これは まったく 自然な結果とは 言えない。
( 実際に 他の項は 無視されている。 )
(Eq.16) ストーナー理論の自由エネルギー。

ストーナー模型では、自由エネルギー F(M,T) は 磁気モーメント (= M ) と 温度 (= T ) の関数である。
"M" に関する 奇数項は 消えることにする。
係数 a(T) と b(T) は 理論そのものから導けず 実験から決定するしかない フリーパラメーターである。
(Eq.17) 磁場 "h"。

Eq.16 と Eq.17 から、磁場 (= h ) は 自由エネルギー (= F ) を 磁気モーメント (= M ) で微分することによって得ることができる。
(Eq.18)

磁気モーメント (= M ) は h × χ (= 磁化率 ) に等しい。
つまり χ の逆数は "h" を "M" に関して微分することによって得られる。
ここで Eq.15 の "IM" 項を この χ に付け加える。
この "IM" は Eq.11 の人為的なトリックによって得られたものである。
そして 相互作用 (= I ) の大きさは 実験をして決定するしか他に方法がない。
(Eq.19)

式を (kT) で展開して いくつかの近似を行うと Eq.19 の関係式を得られる。
これは キュリー・ワイス則と 一致しない。
(Eq.20) Ni の 磁化率は ストーナー模型を満たさない。
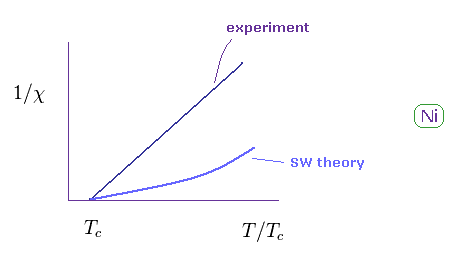
Eq.20 に示したように、この ストーナー模型は 様々な原子において 実験値と 一致しない。
( 近いものもある。 )
また 見てのとおり、この模型自体 かなり粗い近似である。
重要なパラメーター a(T)、 b(T)、 "I" などは 実験から決定するしかない。
(Fig.4) 物性物理学の DFT は 単なる "粗い" 近似である。

密度汎関数法 (DFT) は バンド計算で 頻繁に使用される。
重要な点は DFT は 交換相関エネルギー (= Exc ) などの重要な部分を
計算できない ということである。
彼らは 一様な電子ガスなどの 局所密度近似 (LDA) という粗い近似に頼ることになる。
もちろん、現実の金属が 一様な電子分布でないことは明白である。
そのため この LDA に実験値を再現し得る 擬ポテンシャルなどを人為的にくっつけたりする。
金属は ほぼ 無限の原子を含むため、純粋な 第一原理計算は 不可能である。
もっとも、都合のいい値を与え得るポテンシャルを 選んでいるだけである。
弱い磁気相互作用の場合は、この予測は さらに 困難で 推測の域をでない
つまり 現在のバンド計算は 何らかの実験結果に頼らずに 実際のエネルギーを予測する 力は
ない。
(Fig.5) スピンゆらぎ ?

キュリー・ワイス則は 強磁性の 常磁性相で 成り立つことが知られている。
この現象は ストーナー模型で 説明することができない。
そのため スピンゆらぎ などの 他の効果を ストーナー模型に付け加えることになる。
なぜなら 現在の量子力学には 非現実的な スピンしか 残っていないからである。
この新しい理論は self-consistent renormalization (= SCR ) 理論という。
何度もいうように "スピン" そのものは 完全に 非現実的な概念である。
これはつまり 最新の スピンに基づく理論は ほぼすべてが リアリティーを欠いていることを意味する。
この SCR スピン理論は "スピン"に関する これら人為的なトリックを示す ちょうど良い ( 悪い ) 例 である。
そのため この SCR 理論について ここに書くことに決めた。
(Eq.21)
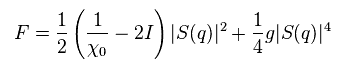
Eq.16 の自由エネルギーで、Eq.18 の 係数 a(T) を用いる。
Eq.16 の b(T) を "g" に変更する。
Eq.16 の F(0,T) の項は 省略した。
すでに述べたように 相互作用の強さ (= I ) は 理論そのものから決められない。
S(q) は スピン磁気振幅と定義する。
(Eq.22) スピンゆらぎ ?
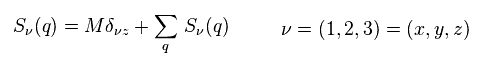
Eq.22 に示したように、磁気モーメント (= M ) は z 軸に 平行である。
Eq.22 の 2項目は スピン揺らぎである。
Eq.22 の2乗は
(Eq.23)
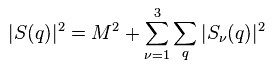
S(q) の4乗は
(Eq.24)

ここで 奇数項は 省略した。
Eq.23 と Eq.24 を Eq.21 に代入して、M2 と M4 の項は
(Eq.25)
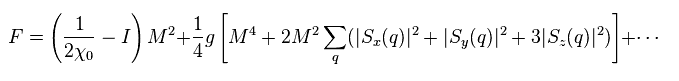
Eq.17 と Eq.18 の関係は
(Eq.26)

Eq.25 を M (= Eq.26 右 ) に関して 2回微分すると、 磁化率 χ の逆数は
( M4 の項を省略して )
(Eq.27)

ここでは
(Eq.28)

ここで、 最も 人為的な トリックを使用する。
彼らによれば 各スピン密度 (= m2 ) は 動的磁化率の 虚数部分に 関係しているらしい。
(Eq.29) スピン = "純虚数" ?

もちろん、 純虚数 "Im χ" は 完全に 非実在的な概念である。
なのに どうして この非実在的な概念が スピン密度として 使われるようになったのだろうか?
ここでは Eq.29 を スピン揺らぎ理論を用いて 導出する。
量子力学によれば、あるスピン演算子 S(t) と ハミルトニアン H の間には Eq.30 の ハイゼンベルクの関係が成り立つとしている。
( ここで "B" は 磁場で、 "H" が 磁気エネルギーである。 )
(Eq.30)

Eq.18 で述べたように、磁化率 (= χ ) は スピン磁気モーメント ( = S ) を 磁場 (= B ) で 割ることによって得られる。
(Eq.31)

ハミルトニアン H は 粒子密度に比例している。
Eq.31 では 係数のいくつかは 省略している。
Eq.31 の2項目で 彼らは 突然 "虚数時間" i/T なるものを 導入したのである。
時間の変数 "t" を t' - i/T (= 虚数時間で もちろん実在しない ) に変更してしまうのである。
(Eq.32) "虚数時間 i/T" は 幻想?

結果的に 彼らは 意図的に 青線の指数関数 (= eωT ) を得ることになる。
これは 明らかに 実験結果などに近付けるための 不自然な操作である。
さらに Eq.31 の 2項目で 虚数時間を採用しておきながら、1項目は 何もせず そのままにする。
Eq.31 の右辺の 1項目と2項目を合計して、次を得る。
(Eq.33)

新しい 指数関数が Eq.33 に現れる ( Eq.31 と比較すると分かる。 )。
次に Eq.33 の "マイナス" を "プラス" に変更する。
(Eq.34)

Eq.33 と Eq.34 から 次を得る。
(Eq.35)

次の関係式を用いて
(Eq.36)
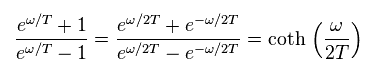
次を得る。
(Eq.37)

Eq.35 の右辺の 虚数 "i" のために、この磁化率 χ は 純虚数になってしまう。
見てのとおり、"スピン" にまつわる これらの値は 完全に非現実的である。
(Eq.38) "純虚数"の磁化率 (= Im χ ) は リアルなのか ?

これが 現在の 最新の スピン理論の 実態である。
物性物理学の現在の物理学者は 物理的実態から離れて 数学的トリックと遊んでいるだけなのである。
つまり スピン自体に リアリティーがないことは お分かりになったと思われる。
coth を 次のように分離する。
(Eq.39)

Eq.29 のスピン密度は
(Eq.40)

ここで Eq.40 の 2項目のみを ピックアップする。
彼らの スピン理論によれば、 中性子の 散乱断面積は Eq.41 のような スピン揺らぎ のようになるらしい。
(Eq.41) 中性子の散乱は 本当に ( 非実在的な ) スピンを示せるのか ?

しかしもちろん、この解釈は 単なる推測にすぎない。
私達は スピン揺らぎそのものを 見ることができない。彼らは 単に 中性子 ( もしくは光 ) などのエネルギー変化を見ているだけである。
また 純虚数の時間や 磁化率に見られるように、これらの数学上のみの概念が 物理的実態に結びつくことは どう考えても不合理で あり得ない。
(Eq.41') 中性子の散乱 = スピン波 ?
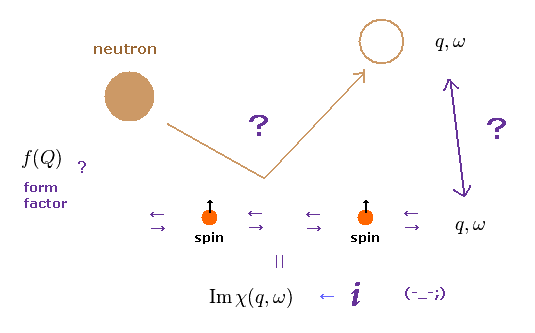
重要な点は Eq.41 の 磁気形状因子 f(Q) は 様々な 他の効果を含んでいるという点である。
つまり 想像上のスピン波が 実際に どのように この形状因子に影響を与えるかは まったく知ることが できない。
彼らによれば、伝導電子のスピンは 原子核の磁気モーメントにも影響を与えうるとしている (= ナイトシフト )。
つまり 何らかの 原子核の磁気共鳴の変化を測定すれば、すなわち それは スピン波だと 唱えるようになってしまった。
またもや 他の様々な効果と スピン波なるものとの 区別をつけることは 不可能である。
しかし 研究者達は スピンが何かを問うことを諦めた状況下においても 論文を 書き続けなければならない。
また この状況では スピンの up と down の 抽象的な数学上の演算子のみしか残っていない。
非現実的な "スピン" を 何かしら別の現実の物に結び付けようとする 彼らの切実な思いが ひしひしと感じられたと思われる。
問題は 純虚数の磁化率 Im χ を どう現実の実験に結びつけるかということである。
彼らは 近似的に この χ を Eq.42 のように表した。
(Eq.42)
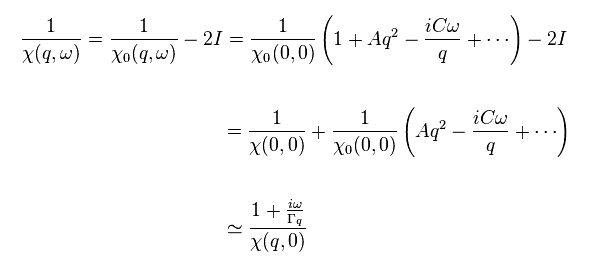
もちろん、Eq.42 の形式や計算過程自体 完全に 人為的な定義によるものである。
つまり 中性子の散乱実験結果に合うように Eq.42 の形式を選んでいるだけである。
これらの A、 C、 ω は 理論そのものから 得ることはできない。
ここで 次のように定義する。
(Eq.43)

さらに 新たな定義を導入後、虚数 χ を Eq.44 のように変えた。
(Eq.44)
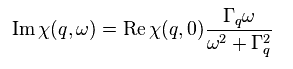
Im χ と Re χ は χ の "虚数"、 "実数" 部分である。
スピン波自体は 直接確認できないため、Eq.44 の関係式は 単なる推測にすぎない。

2013/12/29 updated This site is link free.