
トップページ (正確な新ボーア模型)
ディラック方程式の水素は間違い。
おかしな 超微細構造の解釈 (14/10/15)
(Fig.1) ラムシフトのために "無限大" を人為的に取り除かなければならない。

相対論的な場の量子論 (= このページ ) によれば
2s1/2 と 2p1/2 のエネルギー準位は 共通の j = 1/2 を持つため ちょうど同じになる。
このページに示したように、ラムシフトの測定は 非常に難しく 正確さの点では 非常に曖昧である。
また 彼らは この結果解釈に 想像上の仮定を用いている。
非常に小さな効果 (= 0.0000043 eV、超微細構造レベル ) で 実際に何が起きているのか 実際に見ることはできない。
このラムシフトの値は 非常に 小さいにも関わらず、計算値は 無限大に発散する。
これはつまり ∞ = 0.0000043 eV ということになる。この疑わしい結果を信用できるだろうか?
ディラック自身 人為的な量子電磁力学 (QED) を決して認めることはなかった。
このページで説明するように、ディラック方程式は QED の核心 とも言える部分にも関わらずだ。
(Fig.2) ゾンマーフェルト模型 = ディラックの水素 (= 多くの "架空の" 状態 )。
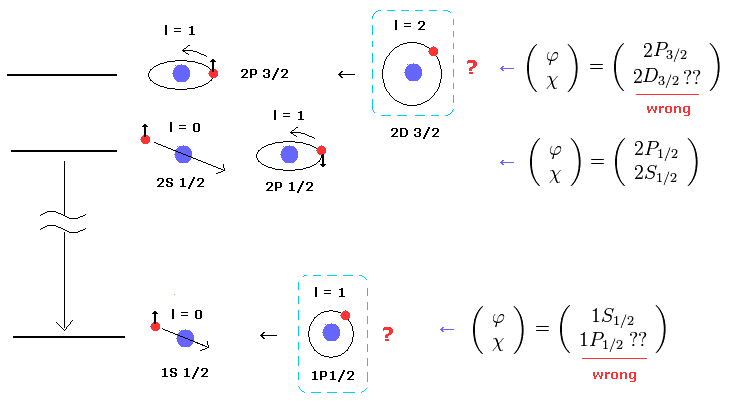
驚くべきことに このページに示したように、まったく異なるメカニズムを用いているにも関わらず、ボーア・ゾンマーフェルト模型は ディラック方程式と まったく同じ結果を与える。
ディラック方程式は 4成分のスピノルからなる。
そのため 上下のスピノルは 違った種類の性質を持つ必要がある。
例えば、 2P3/2 の状態では、上のスピノルが 2P3/2 で、下のスピノルが 非現実的な 2D3/2 状態となる。
なぜなら 2D3/2 は 主量子数 n = 2 で、軌道角運動量が l = 2 のため、これは シュレディンガーの水素原子には 存在しないものだからである。
この結果は 明らかに ボーア・ゾンマーフェルトの微細構造が正しく、ディラック方程式が 間違いであることを示している。
QED のラムシフトは このディラックの水素原子に 完全に依存しているのである。
つまり QED のラムシフトも 間違いということになる。
(Fig.3) ラムシフトは "間違った" 頂点補正 (= g因子 ) を含んでいる。

後で説明するが、ラムシフトは QED のg因子 と共通の頂点補正値を 値の一部として含んでいる。
問題は g因子 (= 異常磁気モーメント ) の計算は 完全に "間違った" 数学に依存しているという点である。
つまり 共通の間違った頂点補正を含む ラムシフトも 間違いということになる。
(Fig.4) "変数変換" ( k = l - β ) は 結果を変えられない。

このページに示したように、 彼らは 変数変換を 利用して g因子の結果自体を 人為的に変えてしまった。
これは 完全に 数学的なトリックであり、計算間違いである。 ( もちろん、 意図的なミスである。 )
なぜなら 変数変換というのは 単なる手段であり、結果自体に影響を与えることは あり得ないからである。
Fig.4 の 一番上の式がゼロのとき、2番目の積分 (= まん中 ) も もちろんゼロになる。
なぜなら それらは 同じ積分だからである。
( 変数変換しただけ。 )
しかし Fig.4 の一番下では 同じ積分が 異なった結果 ( 本来が ゼロで、これはゼロでない ) を出している。
(Fig.5) 非常に小さいラムシフトには 色んな効果が つまっている? = トリック。
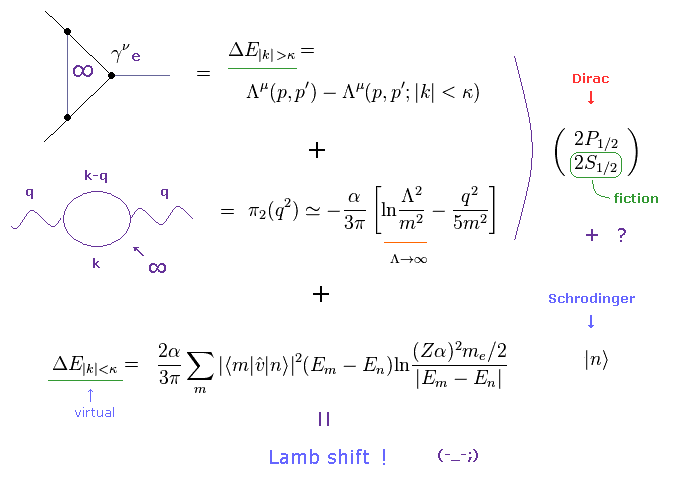
異常磁気モーメントは Fig.3 の 1頂点補正のみから得られる。
一方で、QED のラムシフトは 非常に複雑であり、人為的なトリックで溢れかえっている。
最初に 仮想光子 (= k ) に関して、相対論的な高エネルギー部位と 非相対論的な 低エネルギー部位に 分離する。
さらに、仮想光子の自己エネルギー (= Fig.5 真ん中の真空分極 ) という新たな概念も 実験値に近付けるために組みいれる必要がある。
これらの部分がディラックの水素原子の部分にあたる。
最後に シュレディンガー方程式の摂動部分を計算する。
( 小さな値の中に 非常に多くの効果がつまっていることになる。 )
このページに示したように、ディラックの水素の 下部のスピノルは 架空の間違った状態である。
しかし QED のラムシフトでは、ディラックの水素原子の上下のスピノルを 統合して、さらに それを 仮想の低エネルギーの シュレディンガーの波動関数とに 統合させている。
つまり 彼らは これらの仮想の非実在スピノルを "リアル" な状態として扱っている。
この手法は 明らかに理不尽であり、QED のラムシフトが 間違いであることを示している。
(Fig.6) 2S は 226.4 eV まで励起し、 2p は たったの 13.2 eV まで励起 !?

もっとも重要なトリックは 仮想の (= ランダムな ) 励起エネルギー という概念である。
彼らは 突如として この奇妙な概念を 何の理由もなしに 導入してしまった。
ワインバーグの場の量子論 ( 2巻 ) によれば、2s 状態からの ランダムな 励起エネルギーの平均値は 226.4 eV にもなるらしい。 このサイト (p.6) 参照のこと。
一方で、2p からの励起エネルギーは 小さい 13.2 eV ほどになるらしい。
そもそも 非常に小さなラムシフト (= 0.0000043 eV ) のエネルギー差の中で、電子が常に こんなに大きなエネルギー
(= 226.4 eV ) で 励起を繰り返している という発想自体が あり得ないものである。
また これらのランダムな励起エネルギーは "数値計算" で 近似的にしか求められないらしい。
つまり QED による "正確な" ラムシフト計算というのは 非常に
疑わしいものであることが理解できる。
(Fig.7) ディラックの水素原子の間違った近似

ラムシフトを得るには、2S1/2 などの波動関数を用いなければならない。
しかし QED は 相対論的なディラック方程式を用いており、それには 本来 波動関数としての概念が
ない。
そのため 強引に ディラックの水素の固有関数を 実在の 非相対論的な波動関数に変える必要がある。
このセクションで説明するが、この近似において、彼らは 完全に間違った数学 (= Fig.7 ) に頼っている。
(Eq.1) 電磁場 (= A, V ) と相互作用する ディラックの水素原子
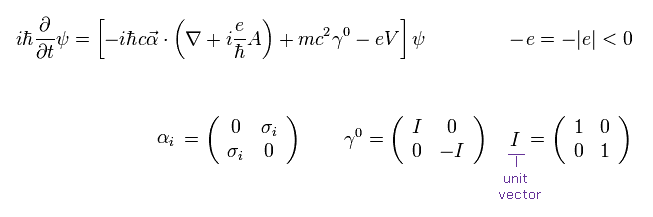
このページに示したように、 Eq.1 は ディラック方程式の水素原子である。
Eq.1 は 電磁場との相互作用を含んでいる ( このページも参照のこと )。
"A" は ベクトル ( 磁気 ) ポテンシャル、 "V" が スカラー ( 電場 ) ポテンシャルである。
σ は パウリ行列である。
もちろん、 ψ は 4成分 のスピノル (= 4 × 1 ) である。
(Eq.2)

Eq.2 に示したように、質量エネルギー (= mc2 ) を 他のスピノル部分から分離する。
つまり φ と χ は 運動エネルギーのみを含んでいると彼らは主張している。
これらの φ と χ は 2成分 (= 2 × 1 ) のスピノルである。
しかし実は 彼らの主張は 下部のスピノル χ に関して 完全に 誤解している。
Eq.2 を Eq.1 に代入して、
(Eq.3)
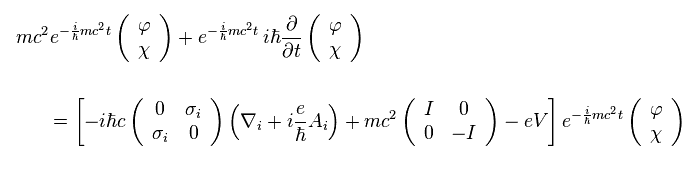
Eq.3 から、上下の式は
(Eq.4)
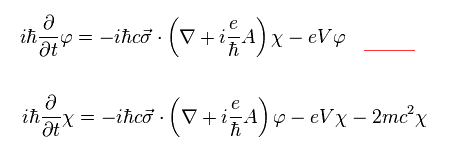
Eq.4 に示したように、上部の式では 質量エネルギーを分離したため、 質量項 (= mc2 ) がキャンセルされている。
しかし 下部の式の ( 負 ) の質量は 元の値の2倍になっている。
そのため 下部の式では 負の質量エネルギーが 増大しており、無視することはできない。
(Eq.5)

ここでは 電磁場を 近似的にゼロと見なす。
(Eq.6)
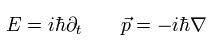
量子力学では、時間と空間の微分は それぞれ エネルギー (= E ) と 運動量 (= p ) の意味である。
Eq.5、 Eq.6 を用いて、 Eq.4 は 近似的に
(Eq.7)
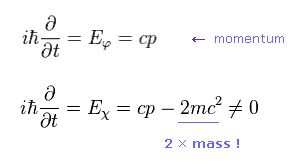
Eq.7 に示すように、 2mc2 の負の大きなエネルギーのために 下部の式のエネルギーは非常に大きくなる。
( つまり ディラック方程式の下部スピノルは 実在の状態ではない。 )
しかし 彼らは ラムシフトを得るために 人為的に このエネルギー値 (= 時間微分 ) を ゼロと見なしてしまった。
(Eq.8) 左辺はゼロ? ← トリック。
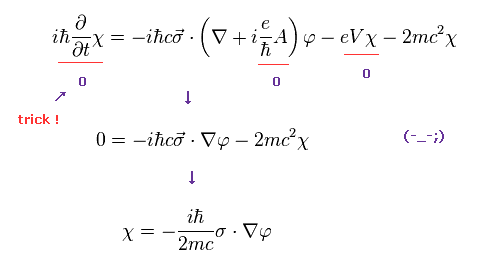
Eq.4 の下の式 ( Eq.8 も参照 ) で、 彼らは 左辺 (= 時間微分 ) のエネルギー項を ゼロと見なして 人為的に除去してしまった。
なぜなら このエネルギー項は 光速 "c" をまったく含んでいないからだと 彼らは主張している。
しかし この解釈は 完全に間違いである。
光速 "c" の値は 暗黙のうちに エネルギー値そのものに含まれているからである ( E = cp )。
Eq.8 を満たすなら、左辺のエネルギー項 (= 時間微分 ) は -2mc2 ほどに大きくなり、ゼロとして無視できない。
つまり この近似は ラムシフトを得るための 人為的な トリックである。
(Eq.9) 仮想光子は 特殊相対論に従わない。

このページに示したように、1つの電子 (= p ) が 光子 (= q ) を吸収、もしくは 放射して、その運動量を p から p' に変えたとする。
このケースで、電子と光子間で エネルギーと運動量保存則が成り立つとすると、この光子 q は 必ず 特殊相対論に 矛盾した存在になる。( アシンシュタインの質量公式で タキオンになる。)
よって この光子 q は "仮想光子" と呼ばれる。
ここでは ( -1, 1, 1, 1 ) バージョンの計量テンソルを用いている。 このページを参照のこと。
(Eq.10) 1頂点補正 → 無限大に発散。

ラムシフトは その一部分として 異常磁気能率 (= g因子 ) の 1ループ頂点補正を含んでいる。
つまり もし QED の g因子の計算が間違いだと、もちろん、QED のラムシフトも 間違いということになる。
ここで Eq.10 のケースを考える。 "q"、 "k"、 "p-k" は それぞれ 仮想光子、光子の伝播関数、電子の伝播関数である。
(Eq.11) g因子を得るには 非現実的な 仮想光子 "q" をゼロにする必要がある。
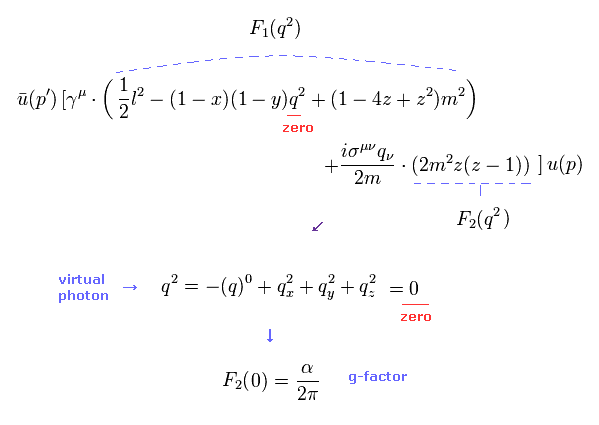
g因子 (= 異常磁気モーメント ) を得るには、 q2 = 0 (= アインシュタインの質量公式 ) の関係式を用いる必要がある。
この光子 q は "仮想の" タキオンであるため、もし この現実的な条件を満足するなら、"q" のエネルギーと運動量のすべての成分はゼロになり、すなわち 仮想光子が 消失することになる。
Eq.11 では "α" は 微細構造定数である。
(Eq.12) 仮想光子 q2 = 0 それとも ゼロでない? どっちが本当?
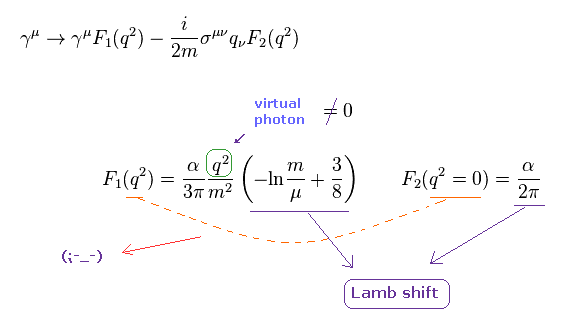
重要な点は ラムシフトを得るには この非現実的な仮想光子の項 (= q2 ) を人為的に 復活させる必要がある。.
Eq.12 の F1 の項が 仮想光子の項である。
一方で、ラムシフトも g因子の項を必要とし、ここでは q2 は ゼロである。
つまり QED のラムシフトは q2 = 0 もしくは ゼロでない 2つの矛盾した項を含んでいることになる。
これは 明らかに自己矛盾であり、QED のラムシフトが 人為的な数学上のトリックであることを示している。
(Eq.13) 高エネルギー項。

赤外発散を避けるために、彼らは 人為的に 高エネルギーと低エネルギーの項を分離した。
Eq.13 は 仮想光子 "k" に関して 高エネルギーの項である。
Eq.13 の右辺の第1項は Eq.12 の 1ループ頂点補正である。
そして 右辺の2項目が ( 相対論的な ) 低エネルギー項で、これは
(Eq.14) 頂点補正における ( 相対論的 ) 低エネルギー項。
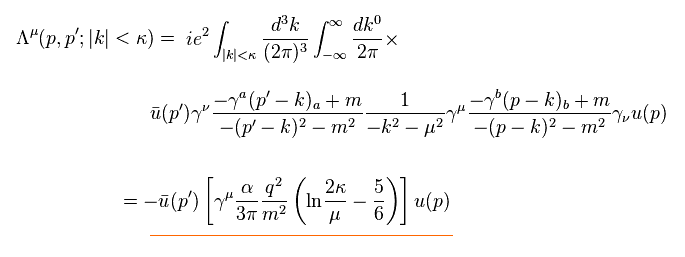
上で述べたように、この q2 は 非現実的な仮想光子の項である。
しかし 彼らは この非現実的な項を 実在の値として用いている。
(Eq.15) 光子の自己エネルギーの真空分極も 必要?
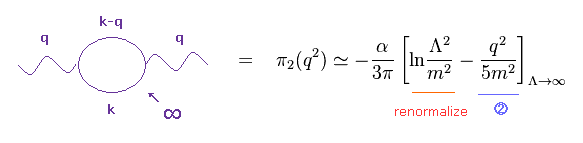
ラムシフトの実験値に近付けるためには 別のタイプの自己エネルギーも 必要不可欠である。 (= 非常に人為的な定義である。 )
Eq.15 は 仮想光子の自己エネルギーで 無限大に発散する。
有限の項のみ ラムシフトの一部として用いる。
このように 彼らは 非常に小さなラムシフトを得るために、意図的に 様々な異なったタイプの効果を 付け加えようとしている。
見てのとおり、QED のラムシフトは 量子電磁力学の 自然な結果とは とてもじゃないが言えないことが分かる。
Eq.12、 Eq.14、Eq.15 を Eq.13 に代入して、次を得る。
(Eq.16) 高エネルギー項 (= 相対論的な ディラックの項 )。

ここで 次の間違った置き換えを使用する。
(Eq.17)

Eq.17 に示したように、 q2 は 本来は 運動量の自乗を 意味していない。光子の質量項 (= ほぼゼロ ) を表している。
しかし 彼らは この (仮想) の質量項 q2 を 運動量 ∇2 に置き換えてしまった。
これは完全に間違った数学である。なぜなら この光子はゼロのエネルギー ( q0 = 0 ) を持つが、その運動量 q は ゼロでは ないからである。
( これは非常に奇妙な粒子である。 )
彼らは ラムシフトを得るために この間違った数学に頼るしかなかったのである。
(Eq.18) スピン = ディラック行列 γ

Eq.18 のように γ 行列で σ を置き換えた。
また 頂点における 電磁場と電子間の相互作用ハミルトニアンは
(Eq.19)

Eq.19 では、 彼らは 磁場 Ai ( i = 1, 2, 3 ) をゼロにし、 A0 をゼロでないとした。
しかし この定義は 後で説明するが矛盾している。彼らは ラムシフトを得るのに ベクトルポテンシャル (= Ai ) の補正を加えるからである。
Eq.16 で、 Eq.17、 Eq.18、Eq.19 を用いて、次の高エネルギー項を得る。
(Eq.20)

ここでは ( c=1, ħ = 1 ) の条件を使っている。
これらの計算や 人為的な定義 ( 置き換え ) に見られるように Eq.20 が QED の自然な帰結とは どう転んでも言い難い。
(Eq.21) 間違った近似。

2S1/2 と 2P1/2 間のラムシフトの値を得るには、 ディラックの4成分のスピノルを シュレディンガーの水素として扱う必要がある。
このページで述べたように、ディラックの下部2成分のスピノルは 実在の状態ではない。
さらに 彼らは ラムシフトを得るには Eq.21 (= Eq.8 ) の 間違った近似を使う必要あがる。
Eq.21 を用いると、Eq.20 の最初の項は
(Eq.22)

ここでは
(Eq.23)

Eq.21 で述べたように、 この ψ (= 4成分スピノル ) は 上部 (= φ ) と 下部 (= χ ) のスピノルから 構成されている。
しかし 彼らは 上部の2成分スピノル (= φ ) のみを 4成分スピノル ψ の代用にしてしまった (= Eq.24 )。これは完全に間違った数学である。
( 4 × 1 スピノル = 2 × 1 スピノル !? )
彼らは この置き換えは 単なる非相対論的な近似であると主張しているが、完全に不合理的な近似と言わざるを得ない。
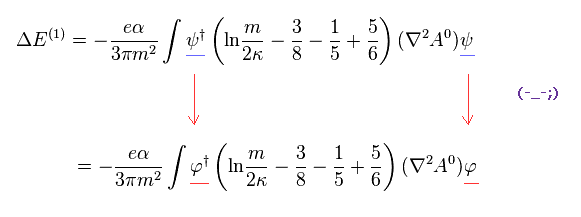
Eq.24 では、元の ψ は 4 × 1 スピノルで、 φ は 2 × 1 (上部) スピノルである。
Eq.20 の2項目は、
(Eq.25)

Eq.24 では 最初の項で 人為的に 4成分スピノル ψ を 2成分スピノル φ に置き換えてしまったが、2項目 (= Eq.25 ) では 上下部両方のスピノルを用いている。
なぜなら Eq.25 は γ 行列を含んでおり、上下部のスピノルをミックスさせるからである。
しかし Eq.25 で 4成分スピノルを用いたのなら Eq.24 でも このスピノルを用いらなければならない。
( これは 明らかに自己矛盾である。 )
(Eq.26) 4成分スピノル → 4成分スピノル。
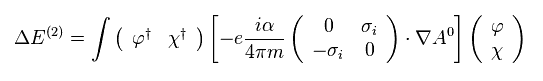
Eq.21 の 間違った近似を Eq.26 に代入して、さらに 次の公式を用いる。
(Eq.27)
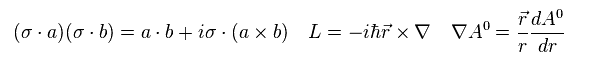
すると 次を得る。
(Eq.28)

(Eq.29) 電磁場と相互作用する シュレディンガー方程式。

上のセクションでは、ディラックの水素の高エネルギー項を計算し、Eq.13 に示すように そこから ディラックの低エネルギー項を取り除いた。
この隙間を埋めるのに、彼らは シュレディンガー方程式の低エネルギー項を用いた。
( この操作は 赤外発散を避けるためと主張しているが、この過程で 様々な誤った 定義を 密かに導入している。 )
(Eq.30) 磁気モーメントだけがゼロでない?

Eq.30 に示すように、彼らは 電磁場との相互作用を考慮したとき、磁気ポテンシャルのみ ゼロでない ( 電場 A0 はゼロ。 ) と仮定した。
このページに示したように、この相互作用ハミルトニアンの 2次の摂動は
(Eq.31)

Eq.31 では、 ( m, k, ε ) は 仮想光子の すべての中間状態の意味である。 .
また "n" は 水素の電子の固有状態である。
(Eq.32)

ベクトルポテンシャル A は、
(Eq.33)
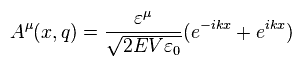
そして 電子の速度 "v" ( 非局所性のシュレディンガー方程式で どうして 速度 "v" が現れたのか 理解できないが・・ ) と 光子の偏光状態 (= ε ) は 次を満たす。
(Eq.34)
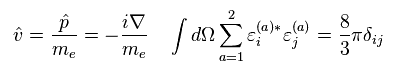
Eq.31、 Eq.33、 Eq.34 を用いると、 シュレディンガーの水素原子の 低エネルギー項は
(Eq.35)

彼らは 電場ポテンシャル (= A0 ) をゼロと仮定した (= Eq.30 ) のに、Eq.35 の最終の式では この電場ポテンシャルを 復活させている。
これもまた 自己矛盾である。
(Fig.35') トリックのサマリー。

彼らは ディラック (= Eq.20 ) と シュレディンガー (= Eq.35 ) の 電場ポテンシャル A0 から 共通の2次導関数 (= ∇2A0 ) が得られたと主張している。
しかし ご覧のとおり、これらの計算過程は 明らかに人為的な操作である。
Eq.16、 Eq.17 に示したように、ディラック部分の2次導関数は非現実的な 仮想光子 "q" に由来する。
この仮想粒子の項で、彼らは アインシュタインの質量公式の定義 q2 = 0 を 運動量の微分 (= ∇2 ) に変えてしたった。
これは明らかに 物理的にも数学的にも 間違っている。
一方で、シュレディンガー部分では、彼らは 最初に 磁気ポテンシャル "Ai" が ゼロでなく、 電場ポテンシャル A0 が ゼロであるとして摂動計算した。
つまり シュレディンガー部分の 2次導関数は Eq.29、Eq.30 に見られるように 磁気 ( 電場でなく ) ポテンシャルなのである。
しかし 最後の形のとき、彼らは 突然 定義を変更してしまい、電場ポテンシャル
A0 のみが ゼロでないとして これをつけ加えた。
これらの操作は 完全に自己矛盾以外何者でもない。
(Eq.36) 小さなラムシフトは たくさんの矛盾した効果でいっぱい??
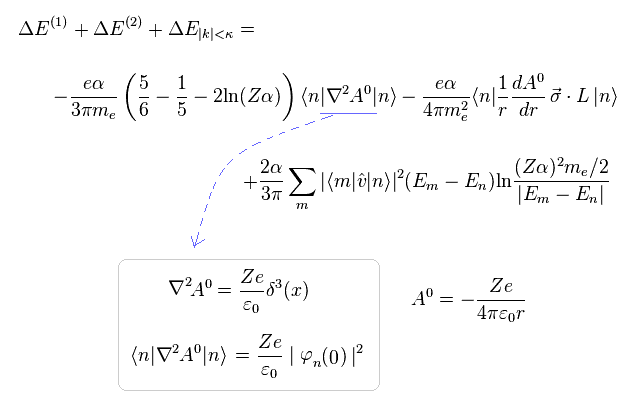
Eq.24、 Eq.28、 Eq.35 を足して Eq.36 のラムシフトの値を得る。
Eq.36 のスピン・軌道相互作用項は、
(Eq.37)

速度 "v" を含む項には 近似的な数値計算に頼る必要がある。
( つまり この部分は 非常に曖昧で疑わしい。)
よって 計算結果は
(Eq.38)

このラムシフトの計算結果は 実験値 1057 MHzと近い。
だから 彼らは QED は 歴史上もっとも成功した理論だと主張しているわけである。
しかし このページを見て分かるとおり、彼らは ラムシフトを得るのに 様々な
間違った数学や 人為的な定義を 駆使しているのが分かる。
彼らは スピン・軌道項を Eq.37 のように置き換えた。
しかし この置き換えは ディラックの水素では 不可能である。
なぜなら ディラックの水素の上下部のスピノルは 異なった軌道角運動量 (= l ) を含んでいるからである。
( 全角運動量 j のみが 共通の値である。 )
(Eq.39) ディラックとシュレディンガーの水素の統合は不可能である。
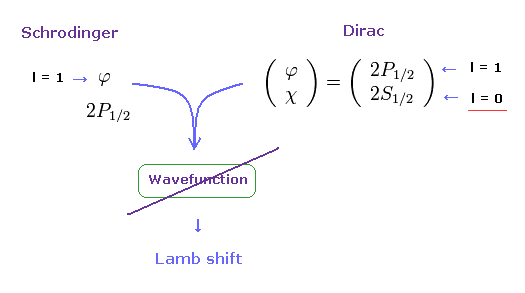
そのため 彼らは 2S1/2 と 2P1/2 の計算の際に 単一の軌道角運動量を決定できない。
つまり この最後の定義も 間違いである。
(Eq.40) 2s と 2p の区別に 人為的なトリックを使用。

このサイトにあるように 水素原子の 2s1/2 と 2p1/2 間には わずか 0.00000437 eV のエネルギー差 (= ラムシフト ? ) があると言われている。
量子電磁力学 (= QED ) に携わる 物理学者達は この非常に小さなラムシフトが QED の正当性を証明したと主張している。
しかし はっきり言って QED の手法によるラムシフトは 非常に人為的な 数学的なトリックで溢れていると言える。
ラムシフトを説明するには 2s と 2p を いかに "都合よく" 区別できるかにかかっている。
これを可能にするには、非常に 非物理的な手段に 頼るしか他に 方法がない。
(Eq.41) ポテンシャルエネルギー (= A0 ) の微分。

クーロンポテンシャルエネルギー (= A0 ) の微分が 電場 (= E ) を与えることが知られている。
さらに 電場の発散は 電荷密度 (= ρ ) を誘電率で割った値になる。
(Eq.42) 電場 (= E ) の発散は 電荷密度 (= ρ ) になる。

水素様原子で、原子核電荷 (= Ze ) が 点状粒子として 原点 (= 0, 0, 0, ) にあるとする。
すると 電荷密度は デルタ関数 (= δ(x) ) を用いて表わされる。
(Eq.43) デルタ関数 = 便利な道具。
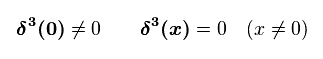
デルタ関数は 原点を除いて 必ず ゼロになる。
2s の波動関数のみ 原点での確率が ゼロでないことから このデルタ関数を 2s と 2p の区別のために利用したわけである。このサイトなど参照のこと。
(Eq.44) "不合理的"な手段に訴えてでも デルタ関数 (= δ ) を得る?

シュレディンガーの水素原子の波動関数は 2s のみ原点での確率がゼロでない。
これを利用して デルタ関数を どんな手段を使ってでも 得ることが大事だと考えたわけである。
しかし この手法の仮定において 様々な 人為的な方法や定義を持ち出しており、すなわち ラムシフトは QED が純粋に予測したものでは ないことが分かる。
(Eq.45) 2s と 2p の両方で、原点での確率密度は "ゼロ" である。

確率密度は 確率振幅 × r (= 半径 ) で 与えられる。
ということは、原点での 確率密度は 2s においても ゼロになる。
しかし この事実を そのまま認めてしまうと、QED で ラムシフトの値を 得ることが できなくなってしまう。
この事実の捻じ曲げも QED の手法が 物理的な見地からしても 間違い であることの証拠である。
(Eq.46) 仮想光子 (= q ) の部分を 意図的に 復活させる。

頂点補正もラムシフトの一部分として 用いられる。
このページに示したように、変数 "q" は 仮想光子 であり、タキオンのごとく 相対論と矛盾した概念である。
つまり、最後のステップにおいて この非実在的な q2 は ゼロになるべきなのだが、ラムシフトでは 意図的に この部分を 復活させて 利用しているのである。
(Eq.47) 仮想光子は 相対論に従わない。

Eq.47 に示したように、この仮想光子は リアルな粒子ではない。
その 全エネルギー (= q0 ) が ゼロ でも、その 運動量 は ゼロにならないのである。 物理的に あり得ない粒子である。
(Eq.48) 人為的な定義。 ↓

ラムシフトを得るには、仮想光子の部分 (= q2 ) から 都合のいい項のみ ピックアップする必要がある。
これは 明らかに 人為的な選択 であり、この時点で 第一原理とは呼べない。
Eq.48 では、 μ が 仮想光子の質量である。
つまり μ が 元のゼロに戻るとき、この項は 無限大に
発散する。
(Eq.49) 非実在の仮想光子 (= q ) を "実在の" 数値を得るのに利用 ?

驚くことに、彼らは この "非実在の"仮想光子 (= q ) を微分演算子 (= ∇ ) に置き換えてしまったのである。
Eq.42 で述べたように、 ポテンシャルエネルギー (= A0 ) の 2階微分は デルタ関数 (= δ ) を与える。
もし このデルタ関数を得ることができれば、2s と 2p を区別できるというわけである。
(Eq.50) ラムシフトは 人為的なトリックの "宝庫" である。

彼らは 真空分極やら 放射やらの 様々な効果を 実験値に近づけるために 盛り込んだ。
これらの項はすべて 非実在の仮想光子 (= q ) を含んでいる。
この仮想光子の運動量の2乗が ポテンシャルエネルギーの2階微分に
変化してしまった。 ( q2 → ∇2 ! )
この非実在の仮想光子に頼るということは 得られた値にも リアリティーはない ということになる。
(Eq.51) "電子" の運動量演算子 (= iħ∇ ) が "光子" の微分に変化 !?

低エネルギー光子の項 (= 非相対論的なシュレディンガーの項 ) では、彼らは ポテンシャルエネルギーの微分形式を得るために 電子の運動量演算子を 利用した。
Eq.51 では、 "A" は ベクトルポテンシャルで、古典的なローレンツ力を表す。
ここから "A∇" の項のみ、相互作用ハミルトニアンとして ピックアップする。
(Eq.52) 相互作用ハミルトニアン (= H' ) の 2次の摂動。

Eq.52 は この相互作用ハミルトニアンによる 2次の摂動 である。
後で、ポテンシャル項 (= A0 ) を この式につけ足すため Eq.50 のように 2次の微分が 得られるというわけである。
非相対論の項は Bethe によって 最初に 得られた。
(Eq.54) 2つのメカニズムはまったく別物なのに 融合?

Eq.50 (= 仮想光子 ) と Eq.52 (= 電子の運動量 ) を比べると、この方法が 非常に 理不尽 でかつ 不合理であることが分かる。
Eq.50 では、2次の微分を得るのに 非実在の仮想光子 (= q ) を用いている。
一方で、Eq.52 では、この導関数に辿りつくのに 実在的な電子の運動量演算子に 頼っている。
驚くことに、ラムシフトを得るのに まったく 異なる概念 を足し合わせているのである。
(Eq.55) 2つの仮想の励起エネルギー。

この 非相対論の項には 2つの異なる種類の 励起エネルギー状態というのが 含まれている ( もちろん、仮想の励起である )。
"Em" は 水素原子における 励起した電子のエネルギーを表している。
"E" は 仮想光子 (= ベクトルポテンシャル A ) の 励起したエネルギーを表している。
もちろん、これらは 人為的に導入された定義であり、まったく QED そのものから導いたものでは ない。
(Eq.56) 余分な項の追加。

ラムシフトを得るには ここで 人為的な項を追加する必要がある。
ある本では これは 質量繰り込みの一種であると書いてあり、別では 真空の光子効果などと書いてある。
しかし これらの説明は 後付けによる言い訳にすぎず、この操作に 物理的な正当性がないことは明らかである。
このトリックを使わないと 上で述べた 微分形式が得られないからである。
ワインバーグの場の量子論 (2巻 ) では、この人為的な質量繰り込みの操作を 色んな理由をつけて正当化しようという努力が見られる。
しかし、この本では パウリ・ビラースの 正則化 で導入した 無限大に重い 仮想粒子の質量 (= Λ だが、この本では "μ" になっている ) を ゼロに近づけようとしている。
もちろん、本来無限大のものをゼロにしてしまったら、元の式の形も変わってしまい、この正則化自体と矛盾してしまうので この方法は理不尽である。
(Eq.57) ポテンシャルの2階微分。

この微分演算子 (= ∇ ) は 電子の運動量 (= ドブロイ波長 ) に由来している。
しかし 彼らは この本来の意味を 都合に合わせて
書き換えてしまった。 ( 電子 → 光子。 )
(Eq.58) 別のトリック。

さらに、様々な障害となる項を ”近似”という名のもとに
人為的に 削除してしまう。
これもまた ラムシフトにおける 重要なトリックである。
(Eq.59) 2S は 226.4 eV まで励起し、 2p は たったの 13.2 eV まで励起 !?

もっとも重要なトリックは 仮想の (= ランダムな ) 励起エネルギー という概念である。
彼らは 突如として この奇妙な概念を 何の理由もなしに 導入してしまった。
ワインバーグの場の量子論 ( 2巻 ) によれば、2s 状態からの ランダムな 励起エネルギーの平均値は 226.4 eV にもなるらしい。 このサイト (p.6) 参照のこと。
一方で、2p からの励起エネルギーは 小さい 13.2 eV ほどになるらしい。
そもそも 非常に小さなラムシフト (= 0.0000043 eV ) のエネルギー差の中で、電子が常に こんなに大きなエネルギー
(= 226.4 eV ) で 励起を繰り返している という発想自体が あり得ないものである。
また これらのランダムな励起エネルギーは "数値計算" で 近似的にしか求められないらしい。
つまり QED による "正確な" ラムシフト計算というのは 非常に
疑わしいものであることが理解できる。

2014/9/27 updated This site is link free.